|
|
|
Copyright © 2004 by the author(s). Published here under license by The Resilience Alliance.
Go to the pdf version of this article.
The following is the established format for referencing this article:
Janssen, M. A. and M. Scheffer. 2004. Overexploitation of renewable resources by ancient societies and the role of sunk-cost effects. Ecology and Society 9(1): 6. [online] URL: http://www.ecologyandsociety.org/vol9/iss1/art6/
Report Overexploitation of Renewable Resources by Ancient Societies and the Role of Sunk-Cost Effects Marco A. Janssen 1 and Marten Scheffer2
1Indiana University; 2Wageningen Agricultural University
- Abstract
- Introduction
- Complexity, Resilience, and the Collapse of Societies
- Empirical Evidence from Studies of Sunk-cost Effects
- Sunk-cost Effects and Archaeological Evidence
- A Minimal Bioeconomic Model of Ancient Societies
- Model Results
- Discussion and Conclusions
- Responses to this Article
- Acknowledgments
- Literature Cited
One of the most persistent mysteries in the history of humankind is the collapse of ancient societies. It is puzzling that societies that achieved such high levels of development disappeared so suddenly. It has been argued that overexploitation of environmental resources played a role in the collapse of such societies. In this paper, we propose an explanation why overexploitation seems more common in ancient societies that built larger structures. This explanation is based on the well-studied sunk-cost effect in human decision making: decisions are often based on past investments rather than expected future returns. This leads to an unwillingness to abandon something (e. g., a settlement) if a great deal has been invested in it, even if future prospects are dim. Empirical study suggests that there are indications of sunk-cost effects in the histories of several ancient societies. A stylized model is used to illustrate under which conditions societal collapse may be expected. Finally, we discuss the consequences of these insights for current societies.
KEY WORDS: bioeconomic modeling, collapse of ancient societies, sunk-cost effect, resilience.
Published: February 5, 2004
“The most important thing we can learn from the past is that no earlier civilization has survived. And the larger the pyramids and temples and statues they build in honour of their god or themselves, the harder was the fall.” Thor Heyerdahl (1998).
The impressive temples and pyramids of ancient times are symbols of mighty societies. How is it possible that such highly developed societies have disappeared? One explanation is that the environmental resource base of these societies was depleted (Tainter 1988, Yoffee and Cowgill 1988, Ponting 1991, Diamond 1997, 2002). The Mayan, Mesopotamian, and Polynesian societies are famous examples of collapses that were likely caused by resource depletion (Tainter 1988, Ponting 1991). Mesopotamia, lying in the river basins of the Tigris and the Euphrates, was able to build up a complex society through intensive agriculture and excessive irrigation. However, their irrigation practices led to a rise in saline groundwater, thus destroying agricultural productivity. In a similar manner, intensive agricultural practices led to soil erosion and decreasing agricultural productivity. The Polynesians who discovered and settled on Easter Island also developed a society in the 1000 years following their arrival, but they deforested the island and greatly reduced the terrestrial resources necessary to sustain the increasing population and ritual activities. Their society had collapsed before the Europeans arrived in 1722.
Tainter (1988) defines collapse as a phenomenon where a society “displays a rapid, significant loss of an established level of socio-political complexity.” The use of the term “collapse” in archaeology is more subtle. Some archaeologists argue that we have to talk about transformations or just abandonment of settlements. In this paper, we may sometimes be less subtle in our use of the word “collapse” than our colleagues in archaeology. In our model, described later in this paper, we do not include socio-political complexity explicitly and, therefore, we refer in our model exercise to collapse simply if population levels decline rapidly and significantly. Many explanations have been proposed for collapses of ancient societies, varying from depletion of vital resources to invasions of barbarians and natural catastrophes (earthquakes, climate shifts, floods, etc.). Tainter proposed an economic explanation of collapse. During development, societies increase in complexity. That is, they comprise more parts and more kinds of parts, and they develop greater integration of parts. At a certain level of complexity, the costs of increasing complexity surpass the benefits, leading to a collapse (Tainter 1988).
In this paper, Tainter's concept is extended using insights from research on human decision making. The central question we address is “why” ancient societies invested beyond an optimal level of complexity, leading to overharvesting of their renewable resources. In our view, an important factor that might explain these systematic dynamics is the “sunk-cost effect”—where human decision making is typically influenced by the level of prior investments (in a wide sense, including capital, experience, and spiritual values). According to conventional economic theory, only the incremental costs and benefits of the current options should be included in decision making. However, as explained in some detail later, numerous examples show that humans do take into account prior investment when they consider what course of action to follow.
As an illustration, consider the case of the Greenland Norse. These colonists might have survived if they had adopted a maritime hunting lifestyle like that of the Greenland Inuit. However, the Norse had made a big investment in inner-fjord pastures to support oversized stone churches and a cathedral, and they were unwilling to abandon this investment, probably because of a sunk-cost effect (Pringle 1997). The economic effects of sunk costs on management of renewable resources have been studied earlier, for example in fisheries (Clark et al. 1979) and the rubber and aluminum industries (Barham et al. 1998). Such economic sunk-cost impacts appear when capital cannot be sold in times of a declining capital stock, which in turn affects strategic investment behavior. Empirical examples show that sunk costs can lead to a hysteresis, that is, a delay in recovery following a recession. These lines of investigation merely consider an economic interpretation of sunk costs (capital investments) to explain observed overcapacities. However, in this study, we elaborate on implications of the sunk-cost effect studied in a broader sense in cognitive science, including various social and psychological factors.
We show that such a sunk-cost effect will tend to keep societies continuing about their business as usual in periods of stress rather than structurally changing their activities or moving to new places with better opportunities. We use simple model analyses to explore under which circumstances the sunk-cost effect should be expected to become most pronounced.
In this paper, we first present Tainter's (1988) economically based framework for explaining the collapse of ancient societies, and discuss how this can be related to the ecological concept of resilience. We then explain the sunk-cost effect, and illustrate that this hypothesis relates to observations in archaeology. Finally, we propose and analyze a bioeconomic model, and discuss the implications of the derived insights for current management of ecological economic systems.
Tainter (1988) argued that there is an underlying process within societies that explains their subsequent collapse. When societies grow, their complexity increases. In the beginning, investments in complexity (for example, in agricultural and resource production, hierarchy, information processing, education, and defense), are beneficial because the easiest, most general, most accessible, and least expensive solutions are attempted first. When the least costly solutions are depleted, and technological development has not provided new ones, more expensive solutions need to be developed for challenges in complex societies. Such solutions to challenges further complexify the society, and, in turn, make solutions in the future even more expensive. As a result (Tainter 1988), the costs of solutions to new challenges in the complex society increase to such a level that a further increase in complexity has negative marginal returns, and the society becomes vulnerable to collapse.
It is important to note the role of technology here. Brunks (2002) argues that “societies always tend to evolve toward the maximum level of complexity that is possible given current technological constraints.” This explains why current societies reach higher levels of complexity than the Romans and the Mayas. We are more efficient at exploiting resources to increase complexity.
Tainter (1988) relates complexity to the size of a society, the number and distinctiveness of its parts, the variety of specialized social roles that it incorporates, the number of distinct social personalities present, and the variety of mechanisms for organizing these into a coherent, functioning whole. With respect to the history of humanity, it is only very recently that complex societies emerged. For most of our history, we lived as low-density hunters and foragers, and there is no simple explanation for the increased complexity, but domestication of plants and animals, the development of agriculture, and the production of regular surplus are factors that contributed to it. Tainter (1988) argues that the development of complexity is an economic process. Complexity levies costs and yields benefits. Assuming that easy solutions are used first, costs of increasing complexity rise faster than the benefits, such that there are diminishing returns to the degree of complexity and, in some cases, even negative returns. For example, simple inexpensive solutions are adopted before moving to the more complex and expensive ones, implying that investments in societies may become more complex over time. Societies initially benefit from increasing complexity because the initial strategies work and give high returns per unit of investment (Tainter 2000). For a period, increasing complexity can continue to generate positive feedbacks. The successful efforts of our ancestors to provide food for an increasing population led to more intensive agricultural practices, as well as continued population growth. However, no society can continue to increase in complexity and maintain stable or increasing returns forever.
As a society increases in complexity, the investments in resource extraction, administration, organization, and defense increase. In the beginning, an increase in complexity is favorable, but there is a decreasing rate of return. This will make the society prone to collapse, because diminishing returns make complexity less attractive and increasing costs of solutions breed disaffection. Taxes and other costs rise to maintain the complexity, but benefits do not rise at the same rate. Finally, the society will reach a point, given technological constraints, beyond which an increase in complexity will lead to negative returns (Tainter 1988).
Why does a society become vulnerable to disturbances at higher levels of complexity? One possible explanation can be found in the concept of resilience. This concept originates from the notion that ecosystems are able to absorb a certain amount of disturbance before they change structurally (Holling 1973). Systems can depart from an equilibrium steady state but remain within a so-called stability domain. In a stability domain, the system is organized into a set of mutually reinforcing structures and processes. If sufficiently large or sufficiently durable, disturbances can cause a system to flip into another stability domain (Scheffer et al. 2001).
The resilience concept explains why, at an increasing level of complexity, ancient societies became vulnerable to disturbances such as droughts (Hodell et al. 1995, 2001, Weiss and Bradley 2001) and earthquakes (Nur and Cline 2000). During the growth phase of a society, a large amount of capital, including infrastructure, organizational structures, and knowledge, is built up, and complexity increases. This complexity reduces short-term variability of supply of food and water within the system.
Figure 1 illustrates the effect of disturbances. We can consider the resource isocline as an equilibrium curve with a catastrophe fold. Stochastic events that reduce the resource abundance (e. g., pests, fires, droughts) may have little effect in small settlements (upper left on R' = 0) but can bring the system across the border of the attraction basin of the overexploited state in large settlements (arrow), resulting in a crash. If sunk-cost effects cause people to leave only at low resource levels, the settlement will grow until point F2 is reached, and a disturbance may cause the system to enter the other domain of attraction, leading the resource to crash, followed by abandonment of the settlement. The resources may recover eventually and a new settlement may be established, resulting in a cyclical development.
Tainter (2000) argues that increase in complexity is necessary to continue providing solutions for increasing population pressure. However, this explanation hardly seems satisfactory. When population pressure is high and increasing complexity brings negative marginal returns, it should, economically, be more desirable to reduce population pressure by, for example, migration. The question thus remains, “why” did ancient societies continue to increase in complexity and population size until they collapsed? In the following section, empirical evidence from animal and human behavior provides a possible explanation.
Economic theory suggests that prior investment should not influence consideration of current options. Only the incremental costs and benefits of the current options should influence the decision. However, there are numerous examples that show that humans do take into account prior investment when they consider what course of action to follow. With regard to human behavior, this is called the sunk-cost effect (cf. Arkes and Ayton 1999) and, in animal studies, it is referred to as the “Concorde fallacy” (cf. Dawkins and Carlisle 1976). The literature on these phenomena is reviewed briefly below.
The poor financial prospects of the Concorde were known long before the plane was completed, but the governments of the United Kingdom and France decided to continue production anyway on the grounds that they had already invested a lot of money. The term “Concorde fallacy” has been used to refer to lower animal behavior in relation to parental investments. Trivers (1972) defined parental investment as “any investment by the parent in an individual offspring that increases the offspring’s chance of surviving (and hence reproductive success) at the cost of the parent’s ability to invest in other offspring.” Typical examples are the defense of a nest and the feeding of young. According to Trivers (1972), in most species, male partners are more likely than female partners to desert the partner and the developing young because, in general, the male partner has invested very little compared with the female partner. Dawkins and Carlisle (1976) argue that Trivers’s reasoning is fallacious. They suggest an alternative reason why an older offspring is preferred. Of two offspring of different ages, the older is preferred not because of the magnitude of the prior investment, but because the expected magnitude of investment in the future is smaller for the older offspring. Thus, consideration of the incremental costs and benefits, not of sunk costs, explains the parental investment decisions. Many studies were carried out over the subsequent 20 years to test the Concorde fallacy for lower animals. However, in a review, Arkes and Ayton (1999) conclude that there is no evidence supporting the Concorde fallacy in behavior of lower animals.
Although lower animals do not seem to suffer from the Concorde fallacy, many studies demonstrate the validity of the sunk-cost effect for humans (Arkes and Ayton 1999). For example, Staw and Hoang (1995) studied the performance of basketball players in the National Basketball Association (NBA). Individuals who were higher draft picks were given greater playing time regardless of the player’s performance. Because higher draft picks cost the team more money, both their greater playing time and their enhanced career longevity are examples of the influence of high sunk costs. Camerer and Weber (1999) tested other explanations against the conclusions of Staw and Hoang (1995), but still found the sunk-cost effect was the dominant explanation. Another example can be found in business. When entrepreneurs have started their own businesses, they are more likely to continue investing in less favorable prospects than are those who have purchased businesses from others (McCarthy et al. 1993).
There is an interesting difference in test results between adults and children with regard to the sunk-cost effect. Children under 10 years of age seem to be less susceptible to the sunk-cost effect than humans of older ages. Arkes and Ayton (1999) explain this by the fact that young humans have more modest cognitive abilities. These cognitive abilities are suggested to be the main explanation for sunk-cost effects, because humans, especially adults, tend to define complex strategies. Such strategies can be highly advantageous in some situations, but they can be detrimental if they are overgeneralized to situations in which such strategies are no longer appropriate. Humans are able to define abstract rules and apply them to new situations.
One rule that can explain the sunk-cost effect is “Don’t waste” (Arkes 1996). This means avoiding abandonment of a (failing) course of action in which resources are already invested. An example is the lost-ticket scenario in which participants are asked whether they would still pay $10 for a theatre ticket after they (1) discover that they have lost a $10 bill or (2) discover that they have lost the ticket. If the ticket was already bought, the participant is much less likely to spend another $10 for another ticket (Tversky and Kahneman 1981). An explanation is that in case (1) the $10 lost was not specifically assigned to the ticket, but in case (2) they had already spent $10 and would thus experience a total price of $20 for the theater ticket.
Escalation of commitment occurs when people or organizations who have committed resources to a project are inclined to “throw good money after bad” and maintain or increase their commitment to the project, even when its marginal costs exceed marginal benefits (Teger 1980, Camerer and Weber 1999). Escalation of commitment is very similar to the sunk-cost effect. Most research is focused on individual decision making. The main explanation for observed escalation is self-justification (Brockner 1992). The idea of self-justification is that people do not like to admit that their past decisions were incorrect and, therefore, are trying to reaffirm the correctness of those earlier decisions.
One might expect that irrational behavior would be corrected in groups. However, many studies suggest that groups make riskier decisions than the mean of decisions made by individuals. In fact, escalation of commitment is found in group decision making (Bazerman et al. 1984). Members of a group strive for unanimity. A typical goal for political decisions within small-scale societies is to reach consensus (Boehm 1996). Once unanimity is reached, the easiest way to protect it is to stay committed to the group’s decision (Bazerman et al. 1984, Janis 1972). Thus, when the group is faced with a negative feedback, members will not suggest abandoning the earlier course of action, because this might disrupt the existing unanimity.
From the literature on the Concorde fallacy, the sunk-cost effect, and escalation of commitments, we can conclude that humans, especially adults, show investment behavior that may be denoted as a sunk-cost effect. In the following sections, we analyze how this effect may explain the overshoot and collapse behavior of ancient societies. The underlying hypothesis is that when a society is totally flexible in its actions, the potential for collapse is reduced. In the case of total flexibility, people will move to other places when the society is confronted with a real scarcity of resources. Due to the sunk-cost effect, they hesitate because they would lose what they have built up in terms of knowledge, social networks, and physical and symbolic capital. People cannot leave without experiencing the costs of losing prior investments. Therefore, they will stay longer, stimulating a collapse of the society as a whole. This may explain why societies increase their complexity above the optimal level.
In this section, we discuss some examples that illustrate possible evidence of the sunk-cost effect in archaeological data. Note that we do not argue that sunk-cost effects are the only or main cause of collapse of ancient populations. However, they may provide further insight into observed collapses.
The prehispanic Pueblo (Anasazi) society provides a prominent example of the possible role of sunk-cost effects. The Anasazi constructed some of the largest non-earthen structures (e.g., Pueblo Bonito, Chaco Canyon, New Mexico) to be built in the USA before the Chicago skyscrapers of the 1880s. In the U.S. Southwest, the Anasazi built simple, small villages, but also large settlements that frequently show evidence of large and labor-costly multi-walled structures that are lacking at small sites. The remains of these Anasazi settlements are especially suitable for testing for sunk-cost effects, because tree-ring analysis of wood artifacts and high-resolution dating of construction activity in the small and large settlements can provide us with estimates of potential annual agricultural production. Janssen et al. (2003) have analyzed data from different settlements: Dolores, and Sand Canyon. They compared timber procurement events, indicating construction activities, against proxies for agricultural production derived from tree rings and they found that people tended to continue to invest in construction at large settlements even in periods of scarcity, whereas construction at small settlements was confined to periods of relative abundance. This is nicely in line with what we would expect from the sunk-cost hypothesis, which states that the more there is invested in a certain settlement, the more likely it is that investments will continue to be made in unfavorable circumstances.
In Sand Canyon, widespread violence during the late 13th century may explain movements from small to large settlements and, therefore, might be an alternative explanation for observed construction patterns (Janssen et al. 2003). However, for the Dolores site, such an alternative explanation does not exist, and the sunk-cost effect provides the only obvious explanation for the observed patterns.
If sunk-cost effects can lead to a collapse, a reduction in sunk costs should help in avoiding a collapse. An indication of this may be found in the history of the Byzantine society, which recovered from a series of crises by deliberately simplifying the complexity of their society (Tainter 2000). During the crises of the 7th century, the Byzantines lost half their empire and their rulers realized they could not continue business as usual. The simplification of the complex society was implemented by removing the structure of ranks and honours, simplifying the civil administration, reducing governmental transaction costs, and cutting the costs of the army. All these changes reduced complexity and (sunk) costs, and were made despite past large investments.
In the introduction, we referred to pyramids as symbols of mighty societies. Within the scholarly literature, this is a topic of debate. Diamond (2003) reviews this debate. Although there is evidence that some of the large pyramids were built before the “mighty” societies, it also seems that the aim of some of the big-structure builders was simply to impress others. Dunham (1994) discusses the temples of the Mayas, which may represent segregation, and thus are not symbols of a mighty unified Maya society. Dunham argues that, at a certain moment, each smaller community built their temples as symbols of independence. Note that these explanations are nonetheless consistent with our interpretation. Large complex structures like temples and pyramids contribute to the sunk-cost effects, together with other investments such as trade networks, roads, armies, palaces, sacred areas, etc.
Consider a stylized model of the long-term development of societies with three modules: the ecological resource dynamics, the human population dynamics, and the human activities. The model builds on the recent line of work in economic literature on ancient societies, such as the studies of Easter Island by Brander and Taylor (1998), Reuveny and Decker (2000), Dalton and Coats (2000) and Anderies (2000), and the study on the competition between Homo sapiens and the Neanderthals by Faria (2000). These models all include renewable resources by a standard logistic function which, together with a simple model of human activities, leads to a bioeconomic model.
Our model includes the basic elements of ancient societies, describing the interactions between resource, population, and sunk costs, in order to understand under which conditions a society may be more likely to collapse.
The renewable resource R is defined as the resource relative to its carrying capacity, and is formulated as a standard logistic model of which a certain amount is harvested. If there is no harvesting, the resource R will grow to amount 1, the carrying capacity of the resource.
 |
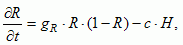[1] |
with the intrinsic growth rate gR and the harvest of the resource by human activities, which depends on the consumption level per capita c (resource amount per person) and the population size H (persons).
Natural growth and migration determine the population of the society. First, we will discuss the population equation without migration. Like Anderies (2000), we distinguish a constant background change rate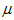 
H and a change rate depending linearly on per capita resource consumption. The rate 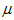H can be interpreted as the net decrease in population
size when the availability of resources is low and relatively more people die than are born. The rate c·e, with e being the person/resource amount, is the health- and culture-related parameter and denotes by how many persons per unit resource consumption the population will increase. Higher levels of resources per capita lead to higher life expectancies, better living conditions, and a higher net fertility rate (survivors 1 year after birth). The population equation is
 |
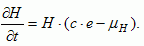[2] |
Adding a migration rate 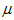m to the standard population model leads to
 |
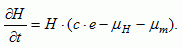[3] |
The migration rate depends on the available natural resources per capita. This indicator denotes that a higher level of natural resources reduces the emigration rate (see equation [4]). When there are no resources left, the total population will leave. Note that we do not explicitly include immigration, which may lead to an increase in population when circumstances in other regions are worse than in the region of interest. Because we do not yet include spatially explicit
information, we omit possible inflow from surrounding regions. The parameter Ro presents a threshold value of resources available per person below which more than 50% of the potential migration flow leaves the region. The parameter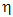 
determines the steepness of the reaction to leave or not when the available amount of resources reaches a certain level. The
migration rate can now be written as
 |
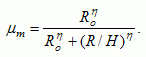[4] |
The threshold Ro indicates when to leave. The lower the amount
of resources per person, the higher the emigration. If 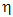is low, the emigration is more or less linear to the average available amount of resources per person (R/H). However, when 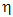is high, emigration is low until the average available amount of resources reaches the threshold Ro and the emigration rate jumps to high levels. The parameter 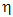refers, therefore, to the response rate of the humans to a changing amount of available resources.
The economy of ancient societies is represented in a very simple way. The population allocates their time to the production and consumption of two goods, the bioresource goods (agricultural output and fish) and manufactured goods (tools, housing, and artistic output) (Brander and Taylor 1998).
A standard utility optimization U().
 |
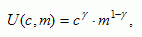[5] |
subject to
 |
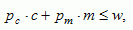[6] |
where m is the consumption per capita of manufactured goods, parameter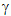 
represents the elasticity of consumption with respect to harvest of the renewable resource. The population derives utility if they consume both bioresource goods and manufactured goods. If
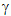< 0.5, which is the case in our default parameter settings, consumption of manufactured goods derives higher utility per unit than consumption of bioresource goods. pc and pm are, respectively, the prices of bioresource and manufactured goods, and w is the wage rate. In this model, the wage rate represents a constraint that enables us to include the trade-off between spending labor to produce bioresource goods and manufactured goods. When the renewable resource is not restricting, optimization of time allocation leads to a fraction 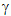to spend on harvesting and a fraction (1-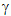) to spend on manufacturing goods. In line with Anderies (2000), we assume that the people need to have a minimum amount of bioresource goods cmin to create a positive utility value. Thus, if the harvested bioresource is less than cmin, the population does not experience a positive utility, due to food scarcity. This leads to the following reformulated utility function:
 |
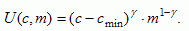[7] |
Assuming a homogenous population of representative agents, we can describe consumption decisions at an individual level and translate them to the population level. In line with Brander and Taylor (1998), we assume linear production functions.
 |
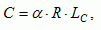[8] |
where C is the bioresource harvest, which is proportional to the product of the size of the resource and the amount of labor, LC, devoted to harvesting bioresources for food consumption. The parameter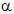 
is a harvesting efficiency coefficient. Manufacturing output, M, is only
related to labor inputs, LM:
 |
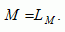[9] |
By calculating the optimal allocation of time to maximize the utility function and by substitution, we derive the actual per capita amount of bioresource and manufactured goods (cf. Anderies (2000) for the derivation):
 |
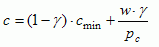[10] |
and
 |
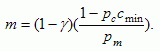[11] |
The harvest of bioresources per capita depends on the amount of resources available and an efficiency parameter, 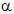(1/(resource amount * person)). The more abundant the resource, the more a person can harvest per unit of time. Because we assume that H = LC + LM, the amount of labor the population should devote to producing bioresource goods and manufactured goods is described as follows (see Anderies (2000) for a detailed derivation):
 |
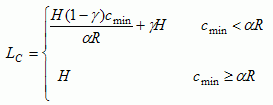[12] |
 |
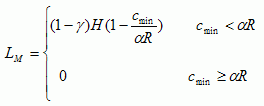[13] |
Thus, when resource availability is low, 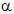R < cmin, all labor is invested in harvesting bioresources for food. When resource availability is higher, part of the labor is spent on manufacturing goods.
For the sake of simplicity, we assume that bioresource goods disappear after consumption, but that manufactured products are accumulated. The stock of manufactured products S increases with investments in manufacturing goods. The manufactured products have an average lifetime of 1/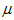k years.
 |
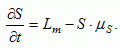[14] |
The stock of manufactured products is assumed to be an indicator for sunk costs because it incorporates the amount of time spent on durable goods and practices. The more time agents spend in producing manufactured products, the more they build up sunk costs, depending on the strength of the sunk-cost effect denoted by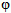 
. We assume that when sunk costs increase, the threshold Ro, when people migrate, increases. Thus, accumulation of sunk costs delays migration.
 |
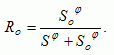[15] |
The default values of the parameters of the stylized model were chosen as follows
(Table 1). The default value for gR is assumed to be 0.04. The value of e is chosen to be 1, which leads to a variable change rate of c, while the constant change rate 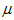H is chosen to be 0.02. The technical coefficient 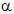is equal to 0.1. The value of the elasticity 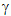is 0.4, in line with Brander and Taylor (1998). The expected lifetime of the manufactured goods 1/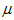S is 10 years. The minimum consumption level cmin is assumed to be equal to 0.02. The response function of Ro is defined by 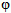equal to 4, and So equal to 0.5. This means that the threshold value Ro drops rapidly when the sunk costs surpass the level 0.5. The response level of 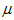m is defined by 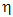equal to 4, leading to a rapid increase in migration when the resource level per capita drops below Ro. The parameter values are not based
on an empirical case, but are educated guesses for a typical society. We have performed a sensitivity analysis to confirm that our qualitative results are robust.
Figure 2 shows the stable cycle with a period of 200 years for the default case. The population grows for almost 200 years, then drops in a few years when
the majority of the population leaves the region. The length of the stable cycle depends on the minimum consumption level cmin and the steepness of the relationship between sunk costs and the relative resource level at which people migrate 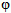(Fig. 3). A higher level of cmin
reduces the length of the stable cycle (to 140 years) and reduces the amplitude. This is caused by the fact that people recognize scarcity sooner, because they require high harvesting levels. A lower value of 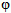, a lower sunk-cost effect, reduced the length of the stable cycle. When responses to sunk costs are less steep, people are less likely to delay their migration.
In Fig. 4, the fraction of time the representative agent is harvesting the bioresource is depicted against the average resource level per capita. At the outset, there is a low resource amount per capita, and the population invests all labor in harvesting bioresources, and reduces the harvesting time gradually when the resource amount per capita increases. The resource amount per capita increases due to a typical population decline in periods of food scarcity. The resource grows faster than the population until, at a certain population size, the resource per capita starts to decrease. When the resource per capita drops below 1, the fraction of time spend on harvesting increases to meet the minimum consumption level.
A more detailed analysis has been performed on the relationship between the sunk-cost effect, the parameter 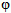, and the minimum level of resource consumption cmin, which indicates a certain lifestyle. The higher cmin, the higher the resource per capita consumption before the population experiences utility of consumption of bioresources. Figure 5 shows that the occurrence of stable cycles is stimulated by a greater degree of sunk-cost effect. Furthermore, the minimum consumption level needs to fit within a specific range. If cmin is low, there is no scarcity and the population reaches a stable high level. If cmin is high, harvesting is so intense that the resource is easily depleted and people leave before they have built up significant sunk costs. The intermediate levels generate enough sunk costs to produce the stable cycle. Figure 6 provides more information by depicting the maximum population size. It shows that the sunk-cost effect is especially important for modest levels of cmin–between 0.01 and 0.04–and leads to a high maximum level of population. The resulting minimum level of population after the crash indicates that this range is the most sensitive for overshoot and collapse (Fig. 7). Note that sunk-cost effects themselves do not lead to overharvest of the resource. Also, without sunk-cost effects, equilibria of low population levels occur (Fig. 6). But inclusion of sunk costs leads to an overshoot and collapse of population levels, rather than evolving to an equilibrium in population level.
In the evolution of civilizations, various parameters that are held constant can change. Technological development improves efficiency (and lowers hmin), but economic development and changing lifestyles increase the minimum level of resource consumption. Only a net reduction of resource consumption can reduce the risk of overshoot and collapse, given the human nature of the sunk-cost effect. We varied the parameters of the model to explore whether the qualitative results hold and, each time, the results verified our insight that the sunk-cost effect together with a modest level of desired consumption from the resource lead to collapse dynamics.
When we include a stochastic element to the model (a random number from a normal distribution with average zero and standard deviation 1 added to the growth rate) and simulate 10 000 time steps, we see periods of ups and downs with and without sunk costs (cmin = 0.02 and 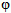= 4) but, when sunk costs are included, the distribution includes more small and large population
levels, suggesting larger booms and busts than would occur without sunk costs (Fig. 8).
Our analysis of the sunk-cost effect in a standard social-ecological model is obviously rather simplistic. There are a number of ways the mathematical model can be improved: (1) the inclusion of more realistic resource dynamics (fast and slow dynamics), (2) a spatially explicit version that focuses on settlement patterns in a landscape, and (3) the inclusion of heterogeneity among agents (different characteristics of households). Such more elaborate models may help explain under which circumstances people can manage resilience of regions properly by allocating pressure on the system in a certain rhythm, and why some ancient societies did not succeed in this. An example of such an analysis is provided by Nelson and Hegmon (2001), who describe the temporal and spatial movement in the 12th century in the eastern Mimbres area, where depopulation of larger settlements might have been a strategy for maintaining occupation continuity in the region.
It may seem that we argue that aggregation of people leads automatically to a collapse. However, there are many obvious benefits of aggregation. In fact, many archaeologists study the formation of states and other hierarchical systems. But, for the sake of analytical transparency, we have discussed only the effects of sunk costs in our stylized model of ancient societies. Note that sunk costs may also provide benefits. If people do not develop any sunk costs, they may use resources according to the “tragedy of the commons.” They enter a region, harvest the resource, and leave. Building up sunk costs offers them the opportunity to learn from the system and to develop effective institutions to regulate the management of the resource. The complex puzzle of evolving institutions has not been included in our simple model of ancient societies.
Despite its simplicity, our analysis suggests that the sunk-cost effect could well be an important factor in explaining overharvesting of resources by ancient societies, leading to their collapse. Historical examples, like that of Anasazi societies, seem in line with our ideas, but a deeper analysis of the archaeological record would obviously be needed to test the sunk-cost hypothesis more rigorously.
As others have argued in this journal (Redman and Kinzig 2003), we believe that the study of ancient societies may also hint at new insights to current social-ecological systems. Besides providing an explanation for collapses of ancient societies, the sunk-cost effect may be linked to current development of social-ecological systems. It seems clear that our current consumption pattern and population growth cannot be sustained forever. Nevertheless, we have thus far found new ways of increasing complexity, such as new technology, without reducing energy consumption and population size. Ultimately, this may not be sustainable, but there are various psychological and economic reasons why our consumption pattern develops the way it does. Perhaps the sunk-cost effect may contribute to the explanation of why people continue to consume resources that are already overharvested.
Certainly, there is abundant evidence that people do not behave like neoclassic models of man (Camerer 2003). Decision making by humans is influenced by issues of fairness and loss aversion (Thaler 1992). The sunk-cost effect is just another example of empirical evidence contrasting with mainstream economic theory. Such insights from experimental social science might help us explain puzzling patterns, such as the collapse of societies, and the persistent question why humans often do not make rational decisions.
Obviously, the link between the mechanisms that may have driven ancient societies into difficulty and current dynamics of societal development remains difficult and we do not wish to extrapolate too much here. Nonetheless, it may be reasonable to expect new collapses of societies. As Thor Heyerdahl (1998) reminds us, this would not be exceptional, but rather a continuation of historical events.
Responses to this article are invited. If accepted for publication, your response will be hyperlinked to the article. To submit a comment, follow this link. To read comments already accepted, follow this link.
The authors thank Nick Abel, Marty Anderies, Buz Brock, Jared Diamond, Carl Folke, Katja Hogendoorn, Garry Peterson, Joe Tainter, Henry Wright, and the participants of the Stockholm Seminar, held December 13, 2001 at the Swedish Royal Academy of Sciences, for their useful suggestions. Special thanks to Tim Kohler who tested the sunk-cost effect hypothesis on Anasazi as published elsewhere (Janssen et al. 2003). The first author gratefully acknowledges support from the Center for the Study of Institutions, Population, and Environmental Change at Indiana University through National Science Foundation grant SBR9521918. We also thank the Resilience Alliance, as it was the visit to the Mayan site El Pilar in Belize during our annual meeting of 2000 that inspired us to work on this subject.
Anderies, J. M. 2000. On modeling human behavior and institutions in simple ecological economic systems. Ecological Economics 35:393–412.
Arkes, H. R. 1996. The psychology of waste. Journal of Behavioral Decision Making 9:213–224.
Arkes, H. R., and P. Ayton. 1999. The sunk cost and concorde effects: are humans less rational than lower animals? Psychological Bulletin 125:591–600.
Barham, B. L., J.- P., Chavas and O. T. Coomes. 1998. Sunk costs and the natural resource extraction sector: analytical models and historical examples of hysteresis and strategic behavior in the Americas. Land Economics 74:429–448.
Bazerman, M. H., T. Giuliano, and A. Appelman. 1984. Escalation of commitment in individual and group decision making. Organizational Behavior and Human Performance 33:141–152.
Boehm, C. 1996. Emergency decisions, cultural-selection mechanics, and group selection. Current Anthropology 37:763–793
Brander, J. A., and M. S. Taylor. 1998. The simple economics of Easter Island: a Ricardo-Malthus model of renewable resource use. American Economic Review 88:119–138.
Brockner, J. 1992. The escalation of commitment to a failing course of action: toward theoretical progress. Academy of Management Review 17:39–61.
Brunks, G. G. 2002. Why do societies collapse? A theory based on self-organized criticality. Journal of Theoretical Politics 14:195–230.
Camerer, C. F. 2003. Behavioral game theory: experiments in strategic interaction. Princeton University Press, Princeton, New Jersey, USA.
Camerer, C. F., and R. A. Weber. 1999. The econometrics and behavioral economics of escalation of commitment: a re-examination of Staw and Hoang’s NBA data. Journal of Economic Behavior and Organization 39:59–82.
Clark, C. W., F. H. Clarke, and G. R. Munro. 1979. The optimal exploitation of renewable resource stocks:problems of irreversible investment. Econometrica 47:5–47.
Dalton, T. R. and R. M. Coats. 2000. Could institutional reform have saved Easter Island? Journal of Evolutionary Economics 10:489–505.
Dawkins, R., and T. R. Carlisle. 1976. Parental investment, mate desertion and a fallacy. Nature 262:131–133
Diamond, J. 1997. Guns, germs and steel: a short history of everybody for the last 13,000 years. Vintage, London, UK.
Diamond, J. 2002. Ecological collapses of pre-industrial societies. Pages 389-406 in G.B. Peterson, editor. The Tanner lectures on human values, Volume 22. The University of Utah Press, Salt Lake CIty, Utah, USA.
Diamond, J. 2003. archaeology: propaganda of the pyramids. Nature 424:891–893.
Dunham, P. S. 1994. Into a mirror darkly: the ancient Maya collapse and modern world environmental policy. Pages 441–468 in J. E. Hickey, Jr. and L. A. Longmire, editors. The environment: global problems, local solutions. Greenwood Press, Westport, Connecticut, USA.
Faria, J. R. 2000. What happened to the neanderthals—the survival trap. Kyklos 53:161–172.
Heyerdahl, T. 1998. In the footsteps of Adam: an autobiography. Little, Brown and Company, London, UK.
Hodell, D. A., J. H. Curtis, and M. Brenner. 1995. Possible role of climate in the collapse of classic Maya civilization. Nature 375:391–394.
Hodell, D. A., M. Brenner, J. H. Curtis, and T. Guilderson. 2001. Solar forcing of drought frequency in the Maya lowlands. Science 292:1367–1370.
Holling, C. S. 1973. Resilience and stability of ecological systems. Annual Review of Ecology and Systematics 4:1–23.
Janis, I. 1972. Victims of groupthink. Houghton Mifflin, Boston, Massachussetts, USA.
Janssen, M. A, T. A. Kohler, and M. Scheffer. 2003. Sunk-cost effects and vulnerability to collapse in ancient societies. Current Anthropology 44(5):722–728.
McCarthy, A. M., F. D. Schoorman, and A. C. Cooper. 1993. Reinvestment decisions by entrepreneurs: rational decision-making or escalation of commitment? Journal of Business Venturing 8:9–24.
Nelson, M. C., and M. Hegmon. 2001. Abandonment is not as it seems: an approach to the relationship between site and regional abandonment. American Antiquity 66(2):213–235.
Nur, A., and E. H. Cline. 2000. Poseidon’s horses: plate tectonics and earthquake storms in the late Bronze Age Aegean and eastern Mediterranean. Journal of Archaeological Science 27:43–63.
Ponting, C. 1991. A green history of the world: the environment and the collapse of great civilizations. Penguin, New York, New York, USA.
Pringle, H. 1997. Death in Norse Greenland. Science 275:924–926.
Redman, C. L., and A. P. Kinzig. 2003. Resilience of past landscapes: resilience theory, society, and the longue durée. Conservation Ecology 7(1):14. [online] URL: http://www.consecol.org/vol7/iss1/art14.
Reuveny, R., and C. S. Decker. 2000. Easter Island: historical anecdote or warning for the future? Ecological Economics 35:271–287.
Scheffer, M., S. R. Carpenter, J. A. Foley, C. Folke, and B. H.Walker. 2001. Catastrophic shifts in ecosystems. Nature 413:591–696.
Staw, B. M. and H. Hoang. 1995. Sunk costs in the NBA: why draft order affects playing time and survival in professional basketball. Administrative Science Quarterly 40:474–493.
Tainter, J. A. 1988. The collapse of complex societies. Cambridge University Press, Cambridge, UK.
Tainter, J. A. 2000. Problem solving: complexity, history, sustainability. Population and Environment 22:3–41.
Teger, A. I. 1980. Too much invested to quit: the psychology of the escalation of conflicts. Pergamon Press, New York, New York, USA.
Thaler, R. H. 1992. The winner’s curse: paradoxes and anomalies of economic life. Princeton University Press, Princeton, New Jersey, USA.
Trivers, R. L. 1972. Parental investment and sexual selection. Pages 136–179 in B. Campbell, editor, Sexual selection and the descent of man, 1871–1971. Aldine, Chicago, Illinois, USA.
Tversky, A., and D. Kahneman. 1981. The framing of decisions and the psychology of choice. Science 211:453–458.
Yoffee, N., and G. L. Cowgill, editors. 1988. The collapse of ancient states and civilizations. The University of Arizona Press, Tucson, Arizona, USA.
Weis, H., and R. S. Bradley. 2001. What drives social collapse? Science 291:609–610.
Address of Correspondent:
Marco A. Janssen first Marco A.
Center for the Study of Institutions, Population, and
Environmental Change, Indiana University, 408 North Indiana Avenue,
Bloomington, IN 47408-3799,USA
Phone: (812) 855-5178
Fax: (812) 855-2634
maajanss@indiana.edu
