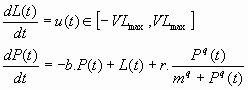
Statement:
Let x be a state in K but outside Viab(K). If x0(.) is the trajectory starting from x = (L, P) satisfying
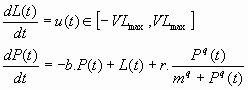 |
[23] |
and governed by controls u0(.) such that
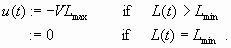 |
[17] |
and if x1(.) is another trajectory starting from x and satisfying Eq. 23, then
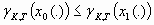 |
[24] |
Proof:
The viability constraints on L(t) are L(t) in [Lmin; Lmax] and d L(t)/dt = u(t). So the viability constraints on L(t) impose the following constraints on u(t):
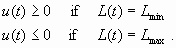 |
[25] |
Furthermore, u(t) is bounded, u(t) belongs to [-VLmax, VLmax].
The control law u0(.) satisfies these constraints and whatever the control law u1(.) satisfying these constraints, u0(y)≤
u1(y) for all states y in [Lmin; Lmax] × [0; +∞].
Furthermore,
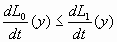 |
[26] |
and
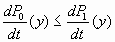 |
[27] |
for all states y in [Lmin; Lmax] × [0; + ∞].
Therefore, as L0(0) = L1(0) and P0(0) = P1(0), for all t in [0, T], L0(t) ≤ L1(t), P0(t) ≤ P1(t), and
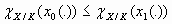 |
[28] |
As
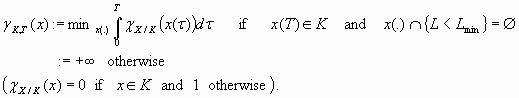 |
[13] |
then
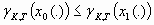 |
[24] |