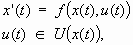
The equation
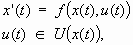 |
[1] |
can also be written under the differential inclusion
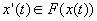 |
[20] |
where
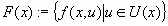 |
[21] |
is a point-to-set map, also called correspondence.
In the model of lake eutrophication,
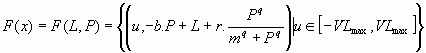 |
[22] |
The question of the determination of the viability kernel (the set gathering all states from which there exists at least one trajectory remaining in K under the dynamics F) can be correctly addressed when F is convex, upper semi-continuous with compact images and K compact.
(i) The image F(x) is bounded and, as the dimension of the state space is finite, it is also compact.
(ii) The convexity of F(x) results from its linearity in u.
(iii) F is differentiable with respect to x in X at fixed u and the components ∂F/∂L and ∂F/∂P are bounded on K. This Lipschitz property of F on
K implies that F is continuous (a fortiori upper semi-continuous).