|
|
|
Copyright © 2003 by the author(s). Published here under license by The Resilience Alliance.
Go to the pdf version of this article.
The following is the established format for referencing this article:
Allen, J. and K. Lu. 2003. Modeling and prediction of future urban growth in the Charleston region of South Carolina: a GIS-based integrated approach. Conservation Ecology 8(2): 2. [online] URL: http://www.consecol.org/vol8/iss2/art2/
Report, part of Special Feature on Urban Sprawl Modeling and Prediction of Future Urban Growth in the Charleston Region of South Carolina: a GIS-based Integrated Approach Jeffery Allen and Kang Lu
Clemson University
- Abstract
- Introduction
- Methodology
- Results
- Discussion
- Conclusions
- Responses to this Article
- Acknowledgments
- Literature Cited
The complexity of urban systems makes it difficult to adequately address their changes using a model based on a single approach. In this research, we developed a GIS-based integrated approach to modeling and prediction of urban growth in terms of land use change. The model was built upon a binomial logistic framework, coupled with a rule-based suitability module and focus group involvement, and is designed to predict land transition probabilities and simulate urban growth under different scenarios. The model was calibrated in the Charleston region of South Carolina through a GIS-facilitated participatory process involving both statistical assessment and human evaluation. The model achieved high overall success rates, although its predictive power varied spatially and temporally with different types of land use. The model was used to predict future urban growth in the region through the year 2030.
KEY WORDS: Charleston, focus group, geographic information system, land use prediction, logistic regression model, rule-based model, urban growth modeling.
Published: November 26, 2003
Historically, South Carolina has experienced little growth. In its early existence, it was an essential agricultural asset to the United States. However, following the Civil War, its growth stagnated for almost a century. In the 1950s and 1960s, South Carolina, and many other regions of the United States, experienced suburban growth at the expense of rural areas and towns (Frey and Speare 1988, Long 1988). This form of urbanization increased dramatically in the 1970s as immigration began to overtake natural increases as the major force for local population changes (Brown and Wardwell 1980). This trend has accelerated over the last two decades, particularly in the coastal regions. A recent change detection study (BCD COG, 1997) shows that, during a 21-year period from 1973 to 1994, urban area in the Charleston region, consisting of the three coastal counties of Berkeley, Charleston, and Dorchester (BCD), grew by 256% while population increased by only 41%. From 1960–1990, urban growth far exceeded population growth at a ratio of 6.2:1, almost triple the national average (2.3:1). The average annual growth rate of this region is 7.24%, four and a half times greater than the U.S. average (1.33%) (Rusk et al. 1997).
Although urban growth is perceived as necessary for a sustainable economy, uncontrolled or sprawling urban growth causes various problems. Not only does urban sprawl rapidly consume precious rural land resources at the urban fringe, but it also results in landscape alteration, environmental pollution, traffic congestion, infrastructure pressure, rising taxes, and neighborhood conflicts. All these have become public concerns, because South Carolina is targeted as one of the top seven retirement states and urban growth continues at a rapid pace. How large will the city become over the next 30 years? Where will the new urban areas be located? What are the consequences of future urban growth? What are the policy implications of new growth? What should be done now to avoid or mitigate negative impacts in the future? Unfortunately, there are as yet no answers to these questions. No urban growth prediction has been made at the regional level in the entire state of South Carolina. Without information generated from reliable predictions, discussions or debates on these issues will remain at a superficial level.
This research, building upon a previous land-use change detection study, was initiated to model and predict future urban growth in the Charleston region. Its objectives are to: a) develop an operational model for regional urban land use change; b) simulate future urban growth in the region based on different scenarios; and c) predict spatial extents of future urban expansions through to the year 2030.
Quantified, visualized, and spatial information on future urban growth obtained through this research will benefit decision-making regarding planning, environmental impact studies, and general public education.
Urban land use modelingUrban growth modeling and prediction history essentially started in the 1950s, showed less activity in the 1970s and 1980s, but has been revived vigorously in the 1990s, thanks to the improvement in spatial data availability and advancements in computer technologies and geographic information systems (GIS) (Wegener 1994). Conflicting views of urban systems (simple vs. complex, static vs. dynamic, ordered vs. chaotic, physical vs. informational, closed vs. open) have led to a variety of different growth theories and models (Wegener 1994, Southworth 1995). Most conventional deterministic models are meaningful (semantics) and operational, but tend to oversimplify the urban reality by not using enough entities and variables (Sui 1997). Successful modeling practices are yet to be reported. The innovative mathematic models, on the other hand, emphasize syntax and urban dynamics, but are difficult to interpret. Their use is still mostly confined to academia. To date, urban modeling and growth prediction remain largely on the frontier of the urban studies field and need further exploration.
Advances in modeling science and predictive methodologies rely on continued improvement in such aspects as model design, variable selection, data quality, and unit of analysis. Urban land use systems are complex systems with components, factors, and agents from both natural systems related to land resources and human systems related to land uses. This implies that a holistic or integrated approach is more appropriate for model design. However, it is impossible to embrace all of these elements within a single model. In essence, all models, simple or sophisticated, are just simplified representations of a complex reality. Essential to a successful modeling process is the identification of key variables (or components) and their interrelations that truthfully represent the urban reality. This certainly necessitates the use of statistical methods such as logistic regression (Landis 1995, Allen et al. 2002). In fact, of about 20 models listed by Wegener (1994) and Southworth (1995), few have been fully validated with empirical data from other areas using a statistical method. In addition, changes in an urban land use system display both regularity and irregularity in temporal rate and spatial patterns. Identification of the rules and their domains (spatial, temporal, and environmental) that govern the regular or ordered change is crucial to the construction of such rule-based models as the cellular automata model (Clarke 1997) and the relative probability model (Pijanowski et al. 1997). Although innovative models are needed to address the irregularity that makes accurate long-term prediction impossible (Casti 1994), scenario-based simulation can provide useful information required for land use planning and environmental impact analysis. It must be pointed out that there are always some intangible variables that cannot be measured and some rules that cannot be mathematically expressed, but their impacts are well perceived by experienced planners or local developers. Therefore, methods are needed to incorporate their knowledge into a modeling process in order to make a more realistic prediction.
This study used a holistic modeling approach, integrating certain chosen components from three different modeling schemes: a) the logistic regression models (Landis 1995) to identify the significant variables and rules that differentiate urban or city from rural and forest environments; (b) the relative probability model (Pijanowski et al. 1997) which uses spatial interactions of neighborhood, distance, patch size (parcels), and site-specific characteristics; and (c) the focus group involvement to create a human input layer, set the growth scenarios, evaluate predictions and disseminate the information. As shown in Fig. 1, the conceptual model framework involves three basic procedures. The first predicts urban transition probabilities with an array of spatial (containing geographic coordinates) data. The second procedure sets urban growth scenarios with aspatial (without geographic coordinates) data. Combining these two procedures yields maps of future urban growth in scenario series (different growth ratios) and temporal series (growth in each successive year). The modeling system was developed as an ArcView Extension® (ESRI, Redlands, California, USA) and integrated with the SPSS Statistical Software Package (SPSS Inc., Chicago, Illinois, USA). The user interface was designed using the Dialog Designer Extension, with the functions written in Avenue Script. The model has several sub-modules designed for data preparation, logistic analysis, growth prediction, error assessment, and map generation. All of them are capable of processing both binary and multiple land use change and prediction.
Data preparation
Urban area used in this research is defined as urban or built-up land according to Anderson’s land use (man-made) and land cover (natural or semi-natural) classification system for use with remote sensor data (Anderson et al. 1976). This land use category includes residential, commercial and services, industrial, transportation, communication, utilities, industrial and commercial complexes, and mixed urban or built-up land. Other remaining land uses are grouped into a single category as non-urban. The reasons for using this binary land use classification are to ensure consistency with the previous land use change detection work done in the region (BCD COG 1997) and to emphasize urban growth as a process of land transformation from natural or semi-natural, non-urban status to a built-up, man-made urban use. The land use data sets were derived from the Landsat Multispectral Scanner (MSS) and Thematic Mapper (TM) imagery collected approximately every alternate year from 1973 to 1994. Therefore, there were 11 data sets, covering a 21-year period, available for model calibration and urban simulation.
Certain issues are involved in the preparation of predictor grids. For grid-based modeling, all data must be converted into grids. Because source data are often collected for other purposes, some predictor grids must be derived from other grids. This process often implicitly involves the use of certain spatial rules. For source data collected in years other than the baseline years, a linear interpolation method was used to estimate the values for the desired year if multiple-year data sets were available; otherwise, the data set closest to the desired date was selected. Even though this procedure introduces a concurrency problem, it was ruled that imperfect data were better than no data in certain instances. In addition, at least two sets of predictor grids had to be prepared: one for the year 1973 for model calibration and another for the year 1994 for prediction. Planned future projects, such as roads, bridges, and utilities, were incorporated into their relevant predictor grids in order to reflect their effects on future urban growth.
The use of finer grids or smaller units is essential to eliminate the “Sin of Grossness” associated with conventional modeling practice (Lee 1973). Although Landis and Zhang (1997) have described conceptually the advantage of using parcels as a base unit of analysis over other zonal units, such as traffic analysis zones or planning districts, and Lu (2001) and Allen et al. (2002) have used parcels for land use change assessment and prediction, these data sets (parcels) were not available for the Charleston region. Consequently, grid units based on initial satellite imagery change detections were used as the base unit of measurement.
Three different sizes of grids were used in this research for different purposes. All variable grids were prepared at 30 x 30 m, equivalent to the spatial resolution of the Landsat TM imagery used to derive urban land use data. They were resampled at 100 and 200 m to create table data sets for conducting statistical analysis (model calibration) at the county and regional levels, respectively. The main purpose was to maintain the data sets at manageable sizes, while keeping the resolution as high as possible. Higher resolution grids (30 x 30 m) were used for the final prediction and mapping in order to obtain a better visual effect.
Prediction of urban transition probabilities was accomplished using an integrated framework composed of a logistic regression model, a rule-based model, and a focus group technique.
Logistic regression modelFor statistical modeling, a multivariate logistic regression model was selected to represent the non-linear nature of urban growth problems (Landis and Zhang 1997). This model is a special case of the multinomial logit model developed by MacFadden (1973) and conceptually based on the random utility theory and discrete choice theory in urban economics and behavior science. Whether the utility of land is measured in terms of consumer benefit, bid-rent, land price, or developer’s profit, it is a function of attributes of land use choices and characteristics of land decision-makers. As in Landis and Zhang’s study (1997), the utility function can be defined as a linear combination of attributes of land use choices:
 |
[1] |
with constant α, coefficients β j ( j = 1, 2, · · ·, k), and predictors X j for k predictor variables ( j = 1, 2, · · ·, k).
Once the landowners or developers make their land use decisions independently with the objective to maximize the utility of their lands, the probability of land transition can be calculated in the following equation
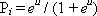 |
[2] |
where P i is the estimated probability that the ith land cell unit ( i = 1,· · ·, n) is urban and u is the utility function usually defined as a linear regression equation.
This linear regression equation creates the logit or log of the odds:
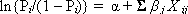 |
[3] |
That is, the linear regression equation is the natural log of the probability of being urban divided by the probability of being non-urban. The procedure employed for estimating coefficients was maximum likelihood, with a goal to find the best linear combination of predictors to maximize the likelihood of obtaining the observed outcome of land use frequencies. Compared with the multinomial logit model, this binary logistic model is extremely flexible and easily applicable (Hosmer and Lemeshow 1989).
In this model developed for the Charleston region, 15 independent variables, derived from a larger initial set of variables, were used to measure physical suitability, accessibility to infrastructure and facilities, market factors, policy constraints, and initial conditions. These variables include 1) forest, slope, wetland, and distance to waterfront; 2) distance to major roads, distance to major node, road density, distance to waterline, and distance to sewer line; 3) population density and cost distance to central business district; 4) existing urban and distance to existing urban; and 5) corporate boundary and protected land. The selection of variables was significantly constrained by the limited availability of spatial data when the project began.
Four separate models were built for the whole Charleston region and its three counties. All four were calibrated using data from 1973 and 1994. They allowed not only logistic regression analysis on each individual model, but also an examination of the spatial variation of the effectiveness of the same logistic framework and the spatial differentiation of the effect of each independent variable. The result obtained was used to select the most appropriate approach or model for the final prediction. In addition to the statistical evaluation, the study compared the maps of observed urban and predicted urban in 1994 to assess the error distribution among different models and counties. This map-based visual analysis helped us evaluate the predictive power of the models in relation to different land use patterns.
In addition to the above error and accuracy assessment, the regional model was validated using a time-series data set for 1975, 1981, 1985, 1989, and 1994 at approximately 5-year intervals. With coefficients derived from the 1973–1994 data sets, the urban area for each of the 5 years was predicted and compared with the observed ones. This method allowed us to examine the reliability of the logistic model over time and test the implied assumption that the relationships revealed by the historical data will hold over different time spans.
Rule-based modelA rule-based model was developed to further enhance the prediction. This model was designed for many reasons. First, the logistic regression model, like all other empirical models, relies on historical data for calibration. It cannot reflect the effects of new land use policies. A rule-based model has the flexibility to incorporate these factors for future prediction. Second, previous studies (Landis and Zhang 1997, Allen et al. 2002) have shown that prediction success rates of logistic models vary substantially (from less than 30% to more than 90%) across geographical regions and across land use categories (Lu 2001). It is appropriate to have an alternative model if the logistic model generates low success rates and its reliability for prediction is doubtful. Third, a rule-based model, if constructed properly, can generate important information, such as building capacity, development potential, infill land, and building suitability (Kaiser et al. 1995). This information is very important to land use decision-making. Finally, the suitability concept is familiar to many planners and several GIS systems have model builders that can facilitate the modeling process.
A hierarchical rule-based model was built to derive relative land suitabilities for urban development (Fig. 2). The rules for rating, ranking, and weighting variables were also grouped into five categories, similar to those independent variables used in the logistic model. Physical suitability rules reflect the on-site relationships between land properties and urban development. Although other human factors play their roles in urban development, physical features are the fundamental determinant for the urban landscape, particularly in water–wetland separated coastal areas or relief-constrained areas. Access orientation rules reflect the off-site effects of infrastructures, facilities, utilities, or services, which are reverse functions of distance and often cause urban space to have linear characteristics. Market orientation rules influence where new urban areas will grow faster when demand (population, employment, or housing) is relatively high but land price is relatively low. The urban-to-urban rule assumes that initial urban will remain urban in the future and land use change from natural to urban is unidirectional. Policy constraint rules guarantee that environmentally important lands (including national forest land, natural reserves and wildlife refuges, state and county parks and other public land, and private land with easement) will be protected from urban development, and urban development is also precluded in environmentally hazardous areas.
The modeling process involves five steps. First, like Pijanowski’s (1997) relative probability model, most variable grids need to be reclassified into ordinal categories based on their suitability for urban development. In this research, a 0–10 scale was used for the classifications, but each ranked grid (R ij) was divided by its maximum value so that its range falls between 0 and 1. Next, the weight factor (w ij) and the exponential factor (k) are assigned to each ranked grid according to the researchers’ knowledge, interactive assessment by the focus group, and the result of the significance test of predictors from the logistic model. Then, the total ranked suitability score (Σw ijRkij) is calculated for each land unit (i) and subsequently divided by the maximum score (max (Σw ijRkij)) found in the region to generate a relative urban transition probability ranging between 0 and 1. Following this, all binary grids (E im) that represent land units unsuitable for urban development due to physical or policy constraints are merged into one grid whose complement is used to multiply the relative probability grid so that these land units are excluded from urban development. Finally, the current urban grid (U i) is overlaid on the resulting grid generated by the above process, so that current urban units remain urban in the future. Therefore, the relative urban transition probability Prob(i) in terms of ranked suitability with constraints can be calculated based on the following formula.
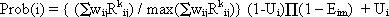 |
[4] |
A focus group approach was used in this research to overcome the deficiency of computer-based artificial intelligence. Due to the complexity of land use systems, many factors or variables cannot be defined or measured, or their relationships cannot be modeled, but their overall intangible effects may well be perceived by people, particularly local planners, developers or experts with years of experience. In this sense, computer-aided land use modeling is not necessarily superior to human-based prediction (Lee 1994). Proper use of a focus group, a collection of the best information processor-human brains, will improve the realism of urban growth prediction.
The focus group consisted of local experts, planners, developers, landowners, conservationists, and community leaders who have a profound knowledge of the region and urban growth factors. Group sessions were organized in different formats (interviews, meetings, and workshops) to accomplish three tasks: a) collect public opinion on urban development to map areas that are most likely to be developed by year 2030; b) evaluate the results of computer-based logistic and suitability predictions; and c) disseminate information about possible future urban growth or urban sprawl.
At the initial stage, the members of the focus group were provided with a base map of the Charleston region and urban land use maps. Each member was asked to mark on the maps or describe the possible urban area or boundary for the next 30 years based on his or her personal knowledge, experience, and intuition. These urban areas were digitized to create a map of the future urban boundary. The map was modified later to reflect subsequent predictions during and after evaluation meetings. Although no attempt was +made to differentiate the development probability within the projected urban area, water bodies and wetlands were excluded later to make it more realistic.
Integrated modelThe outputs of the above three models were linearly combined in an integrated model to generate a hybrid transition probability grid for the final prediction. The integrated model is intended to retain the insight into urban growth as predicted by the focus group, to reflect the effects of new policy factors in the rule-based model, and to maintain the objectivity of the logistic model.
A trial and error method was used to determine the weight factors of the integrated model. Statistical methods were considered inappropriate in this case as the three sub-models were developed based on different assumptions and for different purposes. Initially, the three outputs were weighted equally. The focus group prediction proved to be too strong and became even stronger as the prediction went further into the future. This is mainly because probabilities predicted by the logistic suitability models diminish very quickly with distance to the existing urban area, but the focus group prediction is basically a constant. After several trials, the weight of the focus group prediction was reduced to 10% and the other two predictions were weighted at 45% each. This weight combination appeared to eliminate the strong effect of the arbitrary boundary of the focus group prediction, yet retain the detailed spatial differentiations of transition probabilities predicted by the logistic and rule-based models. The latter allows modelers to map the spatial extents of future urban growth based on different scenarios with relatively small intervals of change in both probability and urban area. As urban area continues to grow, areas with very low transition probabilities become urban. Consequently, a 10% change in the probabilities, which involves a large land area, is sufficient to differentiate future urban areas from other lands.
Growth scenariosGrowth scenarios are the primary assumptions upon which predictions are based. The use of multiple growth scenarios allows us to simulate different urban growth processes, even with aspatial data. Growth scenarios can be expressed implicitly or explicitly as policy constraints, growth rules, growth rates, urban sizes, and the like. In this project, we used different growth ratios as growth scenarios to determine future urban sizes.
Growth ratio, sometimes called sprawl index or sprawl scatter index, is defined as the ratio of urban area growth to urban population growth measured as a percentage. It can be calculated using the following formula:
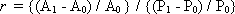 |
[5] |
where r is the growth ratio; P0 is the start-year population; P1 is the end-year population; A0 is the start-year urban area; and A1 is the end-year urban area. Urban size A1 in area is determined by the equation:
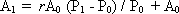 |
[6] |
where urban size A1 depends on the future population P1 and the ratio, r, for both A0 and P0 is given.
Different growth ratios were chosen as growth scenarios for two reasons. First, the concept has been widely used in the literature of urban growth studies and in actual land use planning. It is particularly familiar to the planning community in the Charleston region because of the aforementioned change detection study. Second, a growth ratio reflects the relationship between population growth and urban area consumption. The former is the fundamental force that drives urban land use change, especially in the Charleston region, which mainly consists of tourism and residential communities; the latter has a significant implication for ecological conservation.
It was assumed that population in the Charleston region will grow by 49% from 532,688 persons in 1994 to 795,879 persons in 2030 as predicted by the BCD regional council of government (BCD COG 1997) with information from the U.S. Census Bureau and the South Carolina State Budget Control Board. With this assumption, future urban size will depend only on the growth ratio.
Four factors were taken into account in selecting growth ratios. These factors include the internal historical growth trend, change in external driving forces, focus group output, and regional physical capacity. It was originally assumed that the historical trend revealed by the change detection study will continue through 2030, that is a 6:1 growth ratio will remain unchanged for the prediction period. After detailed discussion with planners and other interest groups, a more conservative ratio of 5:1 was selected as the most plausible scenario. This ratio was considered relatively conservative by many local planners. Higher ratios have been observed since 1994 in the faster growing Mt. Pleasant and Summerville areas. National growth rates for population and urban area expansion support this notion. According to Rusk et al. (1997), many metropolitan areas such as Detroit (13:1), St. Louis (7:1), and Baltimore (5:1), although not necessarily indicative of high growth areas, have seen similar or higher ratios between 1960 and 1990, over an even longer period than the one used in this study. However, the future ratio should not reach the same values, as historical and current urban area and population growth rates exhibit moderate patterns.
At a 5:1 ratio, total urban area will grow by 245% ,from 250.07 square miles to 868.55 square miles by 2030, if the above population projection holds. However, demanded urban areas were also calculated using growth ratios from 1:1 to 6:1 for each of the next 35 years. These values were used to map future urban extents. Although only one population projection was used in the growth scenarios, the effect of the variation in population growth was implicitly left for different growth ratios to account for.
Urban extentsMapping the spatial extent of future urban area was one of the primary tasks of this research. An urban extent is determined by the predicted urban transition probabilities and the chosen growth scenario. It is assumed that the spatial sequence of future urban development will follow the order determined by transition probabilities: the higher the transition probability, the earlier the development of the land cell. Under this assumption, mapping urban extents is a recursive process in which land cells are sequentially selected following their transition probabilities in descending order, until their total accumulated area meets the size of the demanded urban area under certain growth scenarios for a specific year. Three series of maps of the predicted future urban extents were generated as a result of this research. These series include maps for four prediction models, maps for six scenarios, and maps for each year from 1995 to 2030.
The model-series maps were generated mainly to compare the prediction results between different models and to select the best-fit model for the final prediction. The scenario-series maps not only provide valid information needed for policy-making and planning for growth measurement but also facilitate the process of selecting the most plausible growth scenario and the best prediction for the future urban extent. The time-series maps allow the researchers and the focus group to examine future urban growth from scenario–spatial–temporal dimensions. They show when and where land will be converted to urban use under a given scenario. A series of animated imageries were created to simulate the future urban growth process in the region.
The results of the research are reported in three parts: the performance of the integrated model and sub-models tested against the historical data; the focus group evaluation of the future prediction; and more importantly, the predicted urban growth in the Charleston region.
Statistical resultsTable 1 shows the results of the goodness-of-fit tests and prediction success rates of the logistic regression models built for the region and its three counties. All four models were found to be significantly different from the constant-only models (α < 0.05), suggesting that the 15 predictors as a whole are statistically reliable for the prediction of urban transition probabilities in the region.
With 0.5 as the cut-off value for classification (SPSS’s default), the overall prediction success rates of the four logistic models were very good (91.30–94.40%). The success rates for the non-urban use were high (97.77–99.45%), but not impressive for the urban use (28.7–67.1%). However, all four logistic models underestimated the urban areas, as they omitted more urban cells than non-urban cells. This is understandable because the region is still predominantly rural. It is relatively difficult to differentiate dispersed urban cells from rural surroundings. To reduce classification error and to be consistent with future prediction, a case-constraint method was used to select land cells of higher urban transition probability until their area equated the observed or demanded value. As a result, classification accuracy for urban use was improved by about 5–10%, ranging from 49.17–77.10%. Other prediction rates remain above 92% with little change.
Results from both classifications suggest that the logistic regression model generates a better prediction for urban land use in a more urbanized county (Charleston) than in a more rural county (Berkeley or Dorchester). The predictive power of the regional model is moderate, with an accuracy of 65.31% for urban prediction, 96.11% for non-urban prediction, and 93.14% for overall prediction. This model was chosen for the final prediction in order to keep the regional integrity as the tri-county border area is the fastest-growing spot in the region and accounts for a significant portion of the urban area in the relatively rural Berkeley and Dorchester counties.
The parameter estimates of the regional model are shown in Table 2. All independent variables, except for sewer line and slope, were found to be significant predictors (α < 0.05) of urban land use. It is easy to understand why slope is not a significant factor here; the region is located on the flat Atlantic coastal plain. Sewer line is a secondary or tertiary factor compared with other infrastructures and facilities; its spatial extent is largely confined within the scope of the existing urban area; and its effect is reduced due to the use of septic tanks in the rural area. The significant predictors of the regional model include corporate boundary, cost distance, distance to major roads, distance to transportation node, distance to waterfront, distance to waterline, forest land, population density, protected land, road density and wetland. According to the Wald (Table 2) values, distance to existing urban and distance to waterfront, as well as distance to major roads, have greater effects on urban development than any other distance variables used in the model.
It should be pointed out that the effect of each predictor varies geographically from one county to another. All predictors except slope are statistically significant in the model developed for Charleston County, whereas protected land is not a significant factor in either Dorchester or Berkeley counties. This outcome is difficult to understand, particularly in the case of Berkeley as it has two large tracts of protected lands—Francis Marion National Forest and the Naval Weapons Station—located within the county boundary. The relatively low level of urbanization in these two counties could explain the phenomenon, as these protected lands are only smaller portions of the vast undeveloped land and their correlation to urban land use is not strong. In Dorchester County, distance to major roads and distance to waterlines were found to be statistically insignificant. The former may also be related to the relatively low level of urbanization in this county in that most of the major roads in the county run through the rural areas and show little statistical association with urban land use. The latter may be partly due to incompleteness of data or the secondary nature of facilities like sewer lines (Lu 2001).
Table 3 provides a statistical summary of commission and omission errors of the four models. For urban land use, omission error occurs when an urban cell is misclassified into the non-urban category; commission error occurs when a non-urban cell is misclassified into the urban category. With the GIS program, a series of error maps were generated for spatial analysis of error distribution. Unlike prediction success rates, prediction errors increase from the more urbanized county to the more rural county; the errors increase when urban areas are more fragmented, as well as when newly developed land is isolated or far away from the preexisting compact urban core areas (Fig. 3). It appears that urban areas that were omitted (or misclassified as non-urban) are relatively large in size and continuous in distribution, while the majority of non-urban units that were incorrectly committed as urban units are located among the sparsely distributed yet clustered, low density areas. Whether these errors result from the limitation of the logistic framework or the selection of variables and data quality warrants further study.
The regional model was also validated against the historical data collected for each of the 5 years (1975, 1981, 1985, 1989, 1994) to examine the reliability of the logistic model over time. The baseline year was 1975. The urban extent was predicted for each of the testing years and prediction accuracy was assessed against the observed urban use. The results (Table 4) indicate that, with the exception of the period ending in 1989, the accuracy of prediction decreases in all three categories, as the projection period gets longer. In other words, the logistic model becomes less reliable as the projection end year goes further into the future, implying that there is a need for alternative models for longer-term prediction. The exception, that the prediction is better for 1989 than for 1985, is most likely due to the use of the 1990 TIGER road data set for generating the road density variable grid, which was a significant predictor and thus had a stronger effect on the prediction for the closest year. Also, prediction accuracy may change with the magnitude or pace of net change in the urban area, but such a discussion is beyond the scope of this paper.
Focus group evaluation
As there is no developed statistical method to evaluate predictions of future urban growth, the focus group technique was used to make a human intelligence-based assessment on the prediction error of the rule-based suitability model, focus group prediction, and the final integrated prediction. A total of 38 participants were organized into five separate meetings held over two days to assess the overall prediction and select a scenario that they thought the most plausible; to identify the newly developed areas since 1994; and to mark possible growth areas as they projected. Although the purpose of this research is to help understand the overall behaviors of urban growth in the Charleston area, participants were encouraged to comment on the draft maps for the future urban area predicted by the four models (methods). For the first round of meetings, the prediction based on a scenario using a 5:1 ratio was considered the most plausible, and the predictions based on higher growth scenarios were unanimously denied. The prediction based on the integrated GIS model was also considered the best or closest to reality. Figure 3 shows the difference in the predicted urban area between the four models.
Spatially, suburban areas closer to previously developed urban areas were well predicted, with peripheral areas, particularly in Dorchester and Berkeley Counties, slightly under-predicted. Interestingly enough, no substantial urban area was considered over-predicted. Although the assessment was mainly qualitative and spatially vague, the feedback on the perceived error was very useful for model revisions in three ways. First, the identified possible urban areas were incorporated into the map of the focus group prediction to improve the area-based spatial weighting. Second, several key variables, such as distance to corporate areas, major roads, road density, and population density were used to make variable-based weight adjustments so that the core areas of perceived urban growth would be correctly predicted. Third, several variable grids were modified to take into account possible influences from cities, roads, and other features located adjacent to the border but outside of the Charleston region. Edisto Beach, a sea resort town under the jurisdiction of Colleton County but with its hinterland in Charleston County was eventually added to the study area as an integrated part of the Charleston metropolitan system. Later versions of maps were generated with the integrated model based on the 5:1 ratio and were subject to the second and third round of focus group assessments. The weights of variables used in the final rule-based suitability model are shown in Fig. 2.
Predicted urban growthPredicted urban growth in the Charleston region is summarized in Table 5. According to the final prediction, the total population of the region will increase from 532,600 in 1994 to 795,800 in 2030. The net growth is about 263,000 people, or 49.41% within a 36-year period, about 7, 500 people per year. The annual population growth rate is 1.41%. Among the three counties in the region, Charleston ranks first in terms of net population increase, percentage of change, and annual growth rate.
Within the same period, the urban area is predicted to increase by 246.94%, from 250 square miles in 1994 to 868 square miles in 2030. A little over 17 square miles of land will be transformed into urban use each year. As the urban area expands at a rate of about 7% annually, it takes only 16 years to double its size. This means that by 2010, the new urban area will equal and even outsize the old urban area that has existed for several centuries. Charleston County leads all counties in new urban area predicted, even though its growth rate is the lowest. Dorchester County, on the other hand, tops the region in growth rate but has the smallest gain in urban area. Its urban area is most likely to triple. The spatial process of future urban growth is illustrated in Fig. 4. The simulation of urban growth in the region is available on Clemson University's Strom Thurmond Institute website.
Urban area growth will far exceed population growth in terms of percentage of change at a ratio of 5:1 as previously mentioned. As a result, urban population density in the region will drop significantly, from 2130 to 917 persons per square mile, while per capita urban area will increase from 0.3 to 0.7 acres over this period. As predicted, urban area will cover 65% of the total land area in the region by the year 2030. Dorchester will have the highest growth ratio (8:1), while Berkeley will maintain the past regional growth trend (6:1). In either case, an urban sprawl is predicted. Figure 5 compares the predicted urban extents between different growth scenarios.
Figure 6 shows the spatial distribution of the predicted urban extent in the region by the year 2030. Potential urban expansion will follow two patterns: a pattern of lateral growth along the coast on both sides of the City of Charleston and a pattern of landward growth along the major roads. Strongly transportation-oriented in three directions, physically confined by water and wetland, and restricted by the protected land, new urban development will spread in rural areas, along the existing urban fringes, fill in the gaps in old cities, and create a few large urban clusters.
A good land use model should enhance theory and practice (Lee 1994). We believe this research meets these criteria. The model was developed with variables unique to the prediction of urban growth on the Atlantic Coast; it generated quantified spatial information needed for urban planning and impact analysis; it provided visualized, simulated urban growth effective for environmental education; and it has raised urban sprawl issues with the public. Although each of the three sub-models used in this research has been in existence for decades, their integration to predict a complex urban system is a new endeavor. Several issues and implications are worth further discussion.
Modeling issuesThis research has provided a relatively complete test of the logistic model. It validated the model using both geographically differentiated data sets (for the region and the three counties) and temporal series data sets (for five different years). The results are congruent with those of the previous studies (Landis and Zhang 1997, Lu 2001, Allen et al. 2002) in that overall success rates are high but those for urban use are moderate and vary substantially from one geographic unit to another. Although the temporal model validation used the model calibrated with a data set covering a 21-year period and tested against the same baseline year 1973, it is obvious that the prediction becomes less reliable (from 88.15 to 65.31%) as the end year goes further into the future. In other words, the logistic model is appropriate for predictions over a short term (5–10 years) rather than over a long term. Once the prediction horizon exceeds a 10-year span, particularly for a fast-growing region, the reliability of the logistic model is questionable (<75.00%) and alternative methods may be needed. Nevertheless, this does not lessen its value for identifying significant predictors and providing objective statistical assessment. Furthermore, the logistic model has generated better predictions in more urbanized, compact, and continuous areas than in more rural, fragmented, and isolated areas. Whether this resulted from the limitation of the logistic framework, selection of variables, data quality, or complexity of geographic configuration, is worth further study.
The above finding also justified integrating the rule-based suitability model and the focus group technique with the logistic model for long-term prediction. Although the rule-based suitability model is conceptually and structurally similar to the one developed by Pijanowski et al. (1997), it emphasizes the excluding rule (about water, wetlands, and protected lands) and the principle rule (about roads) in a way similar to Clarke’s (1997) study. During the process of model calibration and weight adjustment, we noticed that, as urban area grows through time, only physical environmental factors such as water impose constraints and major roads determine the layout, with protected lands excluded from development. As water bodies and protected lands are easy to identify and are more likely to remain unchanged, proper rating and weighting of roads in relation to existing urban areas are crucial for a reliable long-term prediction. It may be argued that incorporation of focus group “opinions” makes the computer-aided modeling less “scientific.” However, given that the opinions reflect the knowledge and intelligence of these local experts, planners, developers and other professionals that comprise the focus group, we believe the prediction is more realistic. More importantly, with more people involved, the whole modeling process has become a public educational process and the focus group has become a means of information dissemination.
This research faced several limitations and constraints. Even though the computer model is capable of predicting multiple land uses, only two categories were studied here, mainly because the source data set was rich in terms of time series but poor in terms of number of land use classifications. Limited availability and concurrency of spatial data also caused problems in deriving predictor grids for the starting baseline year. The use of interpolation and estimation techniques not only induced errors but also required more skill, effort, and time in data preparation. More importantly, it made the prediction less reliable. Some of these problems can be resolved if change detection and modeling both adopt census years as their baseline years. If 1990 and 2000 are selected as the baseline years, there will be more concurrent (census) data sets available for deriving more socio-demographic variables or interaction variables that could make the model relatively complete. Admittedly, the model was built with consideration of some environmental factors unique to the Atlantic coast. It is an open, operational model that requires only general variables to build and minimal skill to operate. It can be easily applied in other geographical regions to predict land use change at the regional, county, or municipality scale. As parcel data become available for more areas, the model can be refined with finer spatial units. Although the integrated model was used for a long-term prediction, the interpretation of the results should be cautious if the projection period extends beyond two decades. We recommend taking a continuous modeling approach if multi-year data sets are available. Scenario-based simulation is particularly appropriate for long-term prediction. Both statistical results and prediction reliability can be improved if the study area is subdivided into several units in which differentiated rules or relationships can be derived and applied. The focus group’s input can be better documented if interactive mapping or internet mapping techniques are used in a laboratory format. It can also be converted into probabilities based on the fuzzy rule concept.
Environmental implicationsAlthough urban growth has positive economic impacts on the local economy, it has largely negative impacts on the natural environment and coastal ecosystems. Even at a 5:1 growth ratio, which is smaller than the status quo of 6.2:1, urban area in the Charleston region will triple its current size in the next 30 years. In other words, there will be an additional 618 square miles of natural or rural land converted to urban use.
This process inevitably involves altering or destroying natural environments, building barriers to natural processes, and altering natural geo-chemical cycles through pollutant disposal, as well as many other problems. Preliminary overlays of the predicted 2030 urban area over selected resources indicate that 30% of forest land and 50% of cultivated farmland in the region will be lost; 35% of wetlands, 70% of tidal creeks, and 60% of shellfish beds may be impacted; and over 50% of historic landmarks and 30% of archeological sites will be at risk of losing their rural attributes. To prevent these estimates from becoming a reality, we need to change the way we do doing things. To mitigate the negative impacts, critical areas and species should be identified and protected from development; to reduce per capita land consumption, appropriate or higher density of development should be encouraged. To these ends, this modeling project provides quantitative, visual, spatial, and temporal information for planners, environmentalists, and developers.
It is also encouraging that the project has quickly precipitated a number of policy initiatives at the local level, as well as heightened awareness efforts throughout the state of South Carolina. Since the results of the research were reported in the media, a memorandum regarding saving green space through a tax has been proposed to the Charleston County voters. In fact, upon seeing the extent of predicted growth, one local council member stated “I will ensure that this does not happen!” State agencies have established several entities to deal exclusively with smart growth issues at the state level. The research also triggered similar studies in other areas. These include Beaufort-Hilton Head, Myrtle Beach, and the Saluda-Reedy Watershed in South Carolina and the Chesapeake Bay area in Maryland. Regional planners have used time series maps for reevaluation and revision of the comprehensive plan, and the South Carolina Coastal Conservation League relied on the information to launch an educational “Charleston Greenbelt Project.” Both technical solutions and political solutions have their limitations, but educational solutions may be a promising alternative in the long run. It is our hope that this growth prediction model will continue to give the public objective food for thought.
This research took a hybrid approach to modeling and prediction of urban growth in the metropolitan Charleston region. To make the prediction objective, flexible, and realistic, a binary logistic model was integrated with a rule-based suitability model through a participatory process to predict the probabilities of urban transformation. Future urban growth was simulated based on different growth scenarios that related urban area growth with population growth. The logistic model was found useful for identifying significant predictors and has achieved high prediction success rates for all land use categories as a whole, and moderate success rates for the urban use over a 21-year time span. Results of temporal validations indicate that the logistic model is statistically reliable for short-term prediction, but becomes less reliable once the time-span becomes longer. This finding justified the use of a multiple-model approach for long-term prediction. The rule-based suitability model was found to be a complementary alternative in situations wherever physical suitability and major roads are the only determinants for long-term urban growth. The use of a focus group not only made it possible to “operationalize” some intangible variables and evaluate future prediction, but also created an educational opportunity for participants and a means of disseminating information.
Although urban land use is a complex system that imposes a challenge for science and practice, GIS-based urban growth modeling can provide quantified, visualized, spatial information on the future that is otherwise difficult to obtain. Land use modeling is not a computer game; it is an objective prediction. The findings of this research have substantial implications. Even under a conservative scenario, the Charleston region is been predicted to triple its urban area and to face rapid urban sprawl in the next 30 years. The associated land development will inevitably exert tremendous pressure on the natural environment and coastal ecosystems. The model has provided a vision of the future, good or bad, that it is hoped will draw public attention and increase environmental awareness. It is up to the elected officials, community leaders, local planners, landowners, developers, and conservationists to make wise decisions and take appropriate actions.
Responses to this article are invited. If accepted for publication, your response will be hyperlinked to the article. To submit a comment, follow this link. To read comments already accepted, follow this link.
This research was funded by the NOAA Coastal Service Center (NOAA/CSC) through the South Carolina Sea Grant Consortium (SCSGC). The authors greatly appreciate the support of the South Carolina Coastal Conservation League (SCCCL).
Allen, J., K. S. Lu, and T. D. Potts. 2002. A GIS-based analysis and prediction of land-use change in a coastal tourism destination area. In M. I. Miller, J. Auyong, and N. P. Hadley, editors. 2002. Proceedings of the 1999 International Symposium on Coastal and Marine Tourism: Balancing Tourism and Conservation. April 26–29, 1999, Vancouver, British Columbia, Canada. Washington Sea Grant Program and School of Marine Affairs, University of Washington, Seattle, Washington; Oregon Sea Grant College Program, Oregon State University, Corvallis, Oregon; and Oceans Blue Foundation, Vancouver, British Columbia, Canada.
Anderson, J. R., E. E. Hardy, J. T. Roach, and R. E. Witmer. 1976. A land use and land cover classification system for use with remote sensor data. U.S. Geological Survey Professional Paper 964.
Berkeley, Charleston and Dorchester Council of Government (BCD COG). 1997. Twenty year time series analysis of satellite remote sensor data for environmental and developmental change along Coastal Georgia and South Carolina. Final report submitted to NASA via CD ROM.
Brown, D. L., and J. M. Wardwell. 1980. New directions in urban-rural migration: the population turnaround in rural America. Academic Press, Inc. New York, New York, USA.
Casti, J. L. 1994. Complexification: explaining a paradoxical world through the science of surprise. HarperCollins, New York, New York, USA.
Clarke, K. 1997. Long term urban growth prediction using a cellular automation model and GIS: applications in San Francisco and Washington/Baltimore. Paper presented at the International Workshop on GIS in Spatial Population Analysis and Regional Economic Development, March 24–25, 1997. Hong Kong.
Frey, W. H. and A. Speare. 1988. Regional and metropolitan growth and decline in the United States. Russell Sage Foundation, New York, New York, USA.
Kaiser, E. J., D. R. Godschalk, and F. S. Chapin, Jr. 1995. Urban land use planning. 4th edition. University of Illinois Press, Urbana, Illinois, USA.
Hosmer, J. D. W., and S. Lemeshow. 1989. Applied logistic regression. John Wiley, New York, New York, USA.
Landis, J. D. 1995. Imagining land use futures: applying the California urban futures model. Journal of the American Planning Association 61: 438–457.
Landis, J. D., and M. Zhang. 1997. Modeling urban land use change: the next generation of the California urban future model. Paper submitted to the Land Use Modeling Workshop, USGS EROS Data Center, June 5–6, 1997, Sioux Falls, South Dakota, USA. (Online.) URL: http://www.ncgia.ucsb.edu/conf/landuse97.
Lee, D. B. 1973. Requiem for large-scale models. Journal of the American Institute of Planners 39(3): 163–178.
Lee, D. B. 1994. Retrospective on large-scale models. Journal of the American Institute of Planners 60(1): 35–40.
Long, L. 1988. Migration and residential mobility in the United States. Russell Sage Foundation, New York, New York, USA.
Lu, K. S. 2001. A parcel-GIS based multinomial logistic model for destination land use prediction. Dissertation. Clemson University, Clemson, South Carolina, USA.
McFadden, D. 1973. Conditional logit analysis of quantitative choice behavior. In P. Zarembka, editor. Frontiers in econometrics. Academic Press, New York, New York, USA.
Pijanowski, B. C., D. T. Long, S. H. Gage, and W. E. Cooper. 1997. A land transformation model: conceptual elements, spatial object class hierarchies, GIS command syntax and an application for Michigan’s Saginaw Bay watershed. Submitted to the Land Use Modeling Workshop, USGS EROS Data Center, June 5–6, 1997, Sioux Falls, South Dakota, USA. (Online.) URL: http://www.ncgia.ucsb.edu/conf/landuse97.
Rusk, D., J. Blair, and E. D. Kelly. 1997. Debate on theories of David Rusk. Edited transcript of proceedings in The Regionalist 2(3): 11–29.
Southworth, F. 1995. A technical review of urban land use–transportation models as tools for evaluating vehicle travel reduction strategies. ORNL–6881. Oak Ridge National Laboratory, Tennessee, USA.
Sui, D. Z. 1997. The syntax and semantics of urban modeling: versions vs. visions. Paper submitted to the Land Use Modeling Workshop, USGS EROS Data Center, June 5–6, 1997, Sioux Falls, South Dakota, USA. (Online.) URL: http://www.ncgia.ucsb.edu/conf/landuse97.
Wegener, M. 1994. Operational urban models: state of the art. Journal of the American Planning Association 60: 17–29.
Address of Correspondent:
Jeffery Allen
Strom Thurmond Institute,
Clemson University,
Perimeter Road,
Clemson, South Carolina 29634-0125, USA
Phone: (864) 656-0228
Fax: (864) 656-4780
jeff@strom.clemson.edu