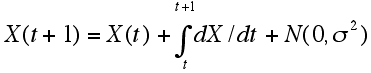
Some readers may find it necessary to download software programs so that they can view the movies below; please keep in mind that not all of these software programs work on all platforms, so some experimentation may be necessary. Possible choices for PCs are Windows Media Player (to download it, click here) and QuickTime (to download it, click here), which is also the best choice for Macs.

Movie 1

Movie 1 shows edge at different scales across a percolation gradient. The density of the sites across the gradient ranges from 100% at each edge for one site state to 0% at each edge for the other state. To view the movie, please click here.

Movie 2

This is a movie of simulated historical change at Eglin Air Force Base (Florida, USA) illustrated using model output. It shows the effects of a policy of fire suppression. The model output is presented in 5-yr time steps for a duration of 50 yr. Each site on the landscape is 60 x 60 m. Light green sites are dominated by longleaf pine, dark blue sites are dominated by hardwoods, and red sites are dominated by sand pine. Dark green sites contain longleaf pine with a hardwood understory. Blue-green sites contain codominant hardwood and longleaf pine. Brown sites contain codominant longleaf pine and sand pine. Lowland forests are represented by light blue and light purple sites that, respectively, do not and do include sand pine. To view the movie, please click here.

Movie 3

This movie shows the dynamics of a stable ball-and-cup model of a simple dynamical system of fire and hardwood dynamics subject to randomly distributed disturbances. To view the movie, please click here.

Movie 4

This movie also shows the dynamics of a stable ball-and-cup model of a simple dynamical system of fire and hardwood dynamics subject to randomly distributed disturbances. In this case, the disturbance history causes the system to switch from a fire-dominated state to a mesic state. To view the movie, please click here.

Model 1

This is an Excel model of the system dynamics model of fire and forest dynamics that includes a variety of graphs illustrating the dynamics of the model. By changing the parameter values of the model, the effects of different parameter values on the dynamics of the model can be assessed. A spreadsheet program such as Microsoft Excel is required to view this model. To view the model, please click here.

The relationship between probabilistic and dynamic systems conceptions can be clarified by considering the behavior of the model described in Appendix 1 with the addition of random noise. Environmental noise can be added to the fire model in Model 1 by shifting the hardwood value by a disturbance that changes the state of the system. I assume that these disturbances are normally distributed, with a mean of zero and a variance of ς ². This addition transforms Eq. A1.3 to

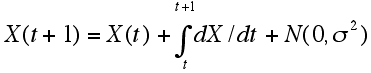(A2.1)

The dynamics of this system are illustrated by envisioning the dynamics of a systems state over a stability landscape, such as the one illustrated in Fig. A2.1. Two examples of the dynamics of this system with ς ² = 0.05 are shown in Movie 3 and Movie 4. The first of these movies shows a case in which the system remains in the state dominated by longleaf pine in spite of disturbance. Despite periodic increases in the density of hardwood, the resilience of the longleaf pine state is not exceeded and it never passes over the peak, i.e., the unstable state discussed in Appendix 1 that separates the stable point for longleaf pine from the stable point for hardwood. The second of these movies (Movie 4) shows a different run of the same model. In this case, a different series of disturbances is enough to push the state of the system out to the longleaf pine attractor, over the peak, and down into the hardwood attractor. These movies illustrate that, as soon as noise is added to the system, the behavior of the system cannot be predicted as easily as with the simple system dynamics model of Appendix 1 was. Although the span of a basin of attraction, i.e., the distance from a stable state to the unstable state, can still be used to measure resilience, a more useful measurement of resilience is the probability that a system state will remain attracted to the same state. This probability must be conditional, because the probability will vary with the length of time that the system is observed and the disturbance regime that the system experiences (in this case, ς ²). To further illustrate the behavior of probabilistic resilience, I estimated the resilience of the longleaf pine state for different fire frequencies and then compared these estimates to the measure of resilience obtained using the system dynamic distance method.

By simulating the behavior of the system shown in the movies 10,000 times, I was able to obtain accurate estimates of the probability that the longleaf state would persist. These results are summarized, along with the standard errors of the estimates, for a range of fire frequencies in Fig. A2.2. The distance measure of resilience is shown for the same system in the absence of noise in Fig. A2.3. Although the measures and the shapes of the graphs are different because of the different methods and definitions they use to measure resilience, the graphs share the same pattern: the decline of resilience as fire frequency increases. This similarity shows the analogy between the distance measure of resilience and the probabilistic measure of resilience while also indicating their differences.