|
|
|
Copyright © 2000 by The Resilience Alliance
The following is the established format for referencing this article:
Riitters, K., J. Wickham, R. O'Neill, B. Jones, and E. Smith. 2000. Global-scale patterns of forest fragmentation. Conservation Ecology 4(2): 3. [online] URL: http://www.consecol.org/vol4/iss2/art3/
A version of this article in which text, figures, tables, and appendices are separate files may be found by following this link.
Report Global-Scale Patterns of Forest Fragmentation Kurt Riitters1, James Wickham2, Robert O'Neill3, Bruce Jones2, and Elizabeth Smith2
1U.S. Geological Survey, Biological Resources Division; 2U.S. Environmental Protection Agency, National Exposure Research Laboratory; 3Oak Ridge National Laboratory
- Abstract
- Introduction
- Methods
- Results
- Discussion
- Responses to this Article
- Acknowledgments
- Literature Cited
- Appendix 1
- Appendix 2
- Appendix 3
- Erratum (Added 3 November 2000)
- Errata (Added 26 January 2001)
We report an analysis of forest fragmentation based on 1-km resolution land-cover maps for the globe. Measurements in analysis windows from 81 km 2 (9 x 9 pixels, “small” scale) to 59,049 km 2 (243 x 243 pixels, “large” scale) were used to characterize the fragmentation around each forested pixel. We identified six categories of fragmentation (interior, perforated, edge, transitional, patch, and undetermined) from the amount of forest and its occurrence as adjacent forest pixels. Interior forest exists only at relatively small scales; at larger scales, forests are dominated by edge and patch conditions. At the smallest scale, there were significant differences in fragmentation among continents; within continents, there were significant differences among individual forest types. Tropical rain forest fragmentation was most severe in North America and least severe in Europe–Asia. Forest types with a high percentage of perforated conditions were mainly in North America (five types) and Europe–Asia (four types), in both temperate and subtropical regions. Transitional and patch conditions were most common in 11 forest types, of which only a few would be considered as “naturally patchy” (e.g., dry woodland). The five forest types with the highest percentage of interior conditions were in North America; in decreasing order, they were cool rain forest, coniferous, conifer boreal, cool mixed, and cool broadleaf.
KEY WORDS: biogeography, edge effect, forest fragmentation, geographic information systems, global patterns, land-cover map, landscape ecology, modeling, perforated forest, remote sensing, satellite imagery, spatial pattern.
Published: September 29, 2000
Humans have dramatically altered the amount, pattern, and composition of global vegetation (Tucker and Richards 1983, Turner et al. 1990, Houghton 1994, Meyer and Turner 1994). Loss of forest and fragmentation of the remainder pose direct threats to biodiversity and endanger the sustainability of ecological goods and services from forestland (e.g., Harris 1984, Lovejoy et al. 1986, Bierregaard et al. 1992, Laurance et al. 1997). The primary concern is direct loss of forest area, and all disturbed forests are subject to “edge effects” of one kind or another. Forest fragmentation is of additional concern, insofar as the “edge effect” is mitigated or exacerbated by the residual spatial pattern (Forman and Godron 1986, Turner 1989, Levin 1992).
Land-cover maps derived from satellite imagery offer outstanding potential for assessing forest fragmentation and its impacts on greenhouse gas emissions, biodiversity, economics, and water quality. Many studies have used satellite imagery to map land cover in remote geographic regions such as boreal forests and tropical rain forests (e.g., Woodwell et al. 1987, Skole and Tucker 1993). Only in the past decade, global maps derived from satellite imagery have made it possible to consistently assess land cover worldwide (Loveland et al. 1999). However, land-cover maps indicate only the location and types of forest, and further processing is needed to quantify and map forest fragmentation (Turner and Gardner 1991, Gustafson 1998).
Most studies focus on the amount of forest, as opposed to its pattern, and forest edge is often visualized as a fixed-width buffer around delineated patches of forest (e.g., Skole and Tucker 1993, Laurance et al. 1998). Our objective was to map and compare global patterns of forest fragmentation by using a model that distinguishes different types of fragmentation. This adds a global perspective to regional studies of forest loss and fragmentation, and thereby helps to evaluate their significance. Knowledge of fragmentation permits some inference about its probable impacts, even without detailed knowledge of all of the ecological processes that might be affected (O’Neill et al. 1997). A global study helps to identify and prioritize regions and organisms for direct measurement of impacts. The risk of future impacts might be related to experience in similar forests elsewhere.
We used 1-km resolution land-cover maps because they were the highest resolution data available for the globe. The Global Land Cover Characteristics database (GLCC; Loveland et al. 1999) includes raster-format land-cover maps derived from satellite (AVHRR) imagery taken from April 1992 to March 1993. We used version 1.2 of the global Interrupted Goode Homolosine equal-area (Goode) map, and the Lambert Azimuthal Equal Area (Lambert) map set for Africa, Australia–Pacific, Europe–Asia (with geographic projection optimized for Asia), North America, and South America. The Europe–Asia map optimized for Europe yielded results that were so similar to the results for the Asia optimization that they are not presented here. The GLCC data are available athttp://edcwww.cr.usgs.gov/landdaac/glcc/glcc.html.
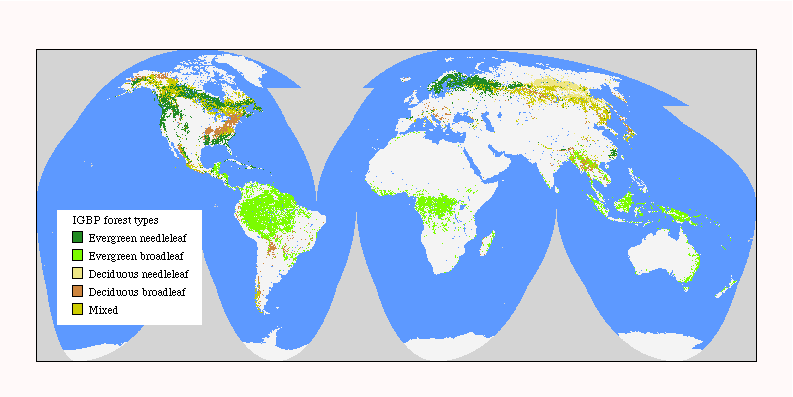
The GLCC database includes several map legends. For calculating fragmentation statistics and for defining the total extent of forest, we combined five of the 17 classes from the International Geophere Biosphere Programme (IGBP) map legend (Loveland and Belward 1997; Fig. 1). We excluded two IGBP classes (woody savanna, savanna) that are considered “forest” by international standards; those classes represent areas with 10–60% tree cover within pixels. For further analysis, we used the Olsen Global Ecosystem (Olsen) map legend (Olsen and Watts 1982, Loveland et al. 1999) to identify 25 types of forest for post-stratification.
Fragmentation model
We measured the amount of forest and its occurrence as adjacent forest pixels within fixed-area “windows” surrounding each forest pixel. That information was used to classify the window by the type of fragmentation. The result was stored at the location of the center pixel. Thus, a pixel value in the derived map refers to “between-pixel” fragmentation around the corresponding forest location. We varied the size of the window, but focused the analysis on the smallest window size.
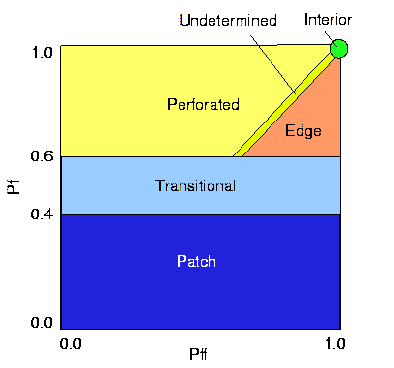
The measurements are illustrated in Fig. 2. Let Pf be the proportion of pixels in the window that are forested. Define Pff (strictly) as the proportion of all adjacent (cardinal directions only) pixel pairs that include at least one forest pixel, for which both pixels are forested. Pff (roughly) estimates the conditional probability that, given a pixel of forest, its neighbor is also forest. Fig. 3 shows the classification model that identifies six fragmentation categories: (1) interior, for which Pf = 1.0; (2) patch, Pf < 0.4; (3) transitional, 0.4 < Pf < 0.6; (4) edge, Pf > 0.6 and Pf - Pff > 0; (5) perforated, Pf > 0.6 and Pf – Pff < 0, and (6) undetermined, Pf > 0.6 and Pf = Pff. [See erratum.]
The rationale for the model is as follows. When Pff is larger than Pf, the implication is that the forest is clumped; the probability that an immediate neighbor is also forest is greater than the average probability of forest within the window. Conversely, when Pff is smaller than Pf, the implication is that whatever is nonforest is clumped. The difference (Pf – Pff) characterizes a gradient from forest clumping (“edge”) to nonforest clumping (“perforated”). When Pff = Pf, the model cannot distinguish forest or nonforest clumping. The case of Pf = 1.0 (“interior”) represents a completely forested window for which Pff must be 1.0.
Forest edges and perforations have less meaning where the amount of forest is low, and percolation theory (Stauffer 1985) identifies two critical values of Pf. Imagine a completely forested landscape represented by a grid of pixels. For completely random forest conversion on an infinite grid (and evaluating adjacency in cardinal directions), the residual forest is guaranteed to occur in identifiable patches when Pf falls below a critical value of about 0.4. Below that value, the nonforest pixels form a continuous path across the window. Conversely, as long as the residual forest is above a critical value of about 0.6, the forest pixels form such a path, and forest edges and perforations have more meaning. These values were used to define the “patch” and “transitional” categories, recognizing that they are approximate because actual land-cover pattern is not random.
ImplementationWe used a “sliding window” algorithm with overlapping windows (e.g., Riitters et al. 1997) to apply the model to about 30 x 106 “forest” pixels on the IGBP map. If the center pixel was not forest, then a null value was assigned to that location. Water pixels were treated as missing values and were ignored in calculations. We used windows of 81 km 2 (9 x 9 pixels, “smallest” scale), 729 km 2 (27 x 27), 6561 km 2 (81 x 81), and 59,049 km 2 (243 x 243, “largest” scale) for the Goode (global) map, and the 81-km 2 window for the Lambert (continental) maps.
No single scale or window size can be correct for all purposes. We focused the analysis on the smallest scale (alternatively, the highest resolution) that was practical, given the data characteristics (O’Neill et al. 1996). The key constraint was the number of pixels needed to reliably estimate a proportion. In comparison to a rule of thumb that 50 observations are needed, a 9 x 9 pixel window could contain up to, say, 40% missing values (water) and still yield a fairly reliable estimate of Pf. This was a useful feature as the sliding window passed near coastlines. The potential number of adjacent pixel pairs for estimating Pff in a 9 x 9 pixel window is 144, but the number of pairs used in the model varies with the amount of forest, and depending on its location, a missing pixel results in one to four missing pixel pairs.
The smallest scale continental maps were post-stratified by Olsen forest types for comparisons. This characterizes pixels of Olsen forest types by the fragmentation of a more coarsely defined forest. The rationale was that fragmentation is a contextual measurement for which differences among forest types are not meaningful. A secondary consideration was that the thematic accuracy of a one-class forest map was expected to be much higher than that of a 25-class forest map. But it is also reasonable to pre-stratify by Olsen forest type prior to applying the fragmentation model; in that case, the fragmentation category would refer to a particular forest type and the analysis would be conducted separately for each forest type. In Appendix 1, we compare pre- and post-stratifying and conclude that the differences were not important at the scale that we used for comparisons of Olsen forest types.
Example
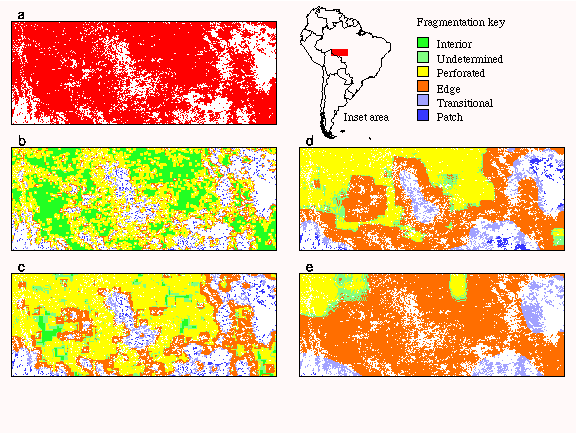
The effects of window size are illustrated (Fig. 4) in the Rondonia region of South America. Fig. 4(a) shows the distribution of forest (red) and nonforest (white) land-cover types. Figs. 4b–e show the results of the fragmentation model with progressively larger window sizes. In this example, interior forest decreases rapidly with increasing window size because the strict criterion (Pf = 1.0) quickly becomes difficult to achieve, even in mostly forested areas such as Rondonia.
Patch areas in the center of the region exist only over a range of scales before being subsumed into edges, whereas patch areas in the southwest part of the region persist at larger scales. Patch areas disappear where it becomes easier to exceed the threshold value (Pf = 0.4) in larger windows. Large regions of perforated forest in the southeast part of the region become transitional forest with increasing window size.
Edge and perforated conditions are dominant for the two largest window sizes, and the undetermined condition generally appears as a boundary between the two. For the largest window size, most of the Rondonia region is edge because only parts of a larger entity that extends outside of the region are perceived at this scale. To help rationalize the differences across scales, consider that larger windows capture lower frequency patterns and smaller windows capture higher frequency patterns.
The digital maps that were produced for this report may be downloaded with metadata from Appendix 3. Six maps portray the fragmentation categories as shown in Fig. 5 and Figs. 9–13 of this report. The other 12 maps portray Pf and Pff for five continents and for the globe; these are not shown in this report, but are included so that others may develop and apply alternatives to the model used here.
Global maps of fragmentation for four window sizes are shown in Figs. 5–
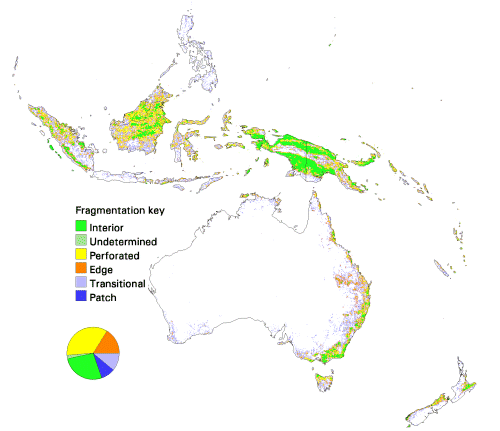
Continental maps of fragmentation at the smallest scale (81 km2) are shown in Figs. 9–
a Areas, measured in thousands of square kilometers, are from the IGBP continental land-cover maps, excluding savanna and woody savanna forest types.
The continental fragmentation maps (Figs. 9–
aForest area (thousands of square kilometers) after intersecting with the IGBP forest map, which recognizes less forest than does the Olsen forest map.
a "Before" refers to pre-stratification of the IGBP forest map prior to calculating fragmentation, and "after" refers to post-stratification.
Forest types with a relatively high percentage (> 40%) of interior area are mostly those at higher latitudes in Europe–Asia and North America, although some tropical and subtropical forest types also have high percentages of interior conditions. The eight forest types with a relatively high amount (> 40%) of perforated area include a variety of tropical, temperate, and boreal types. Only one forest type (conifer in South America) has edge conditions exceeding 40%. There are 11 forest types for which the combined area of transitional and patch conditions exceeds 40%.
Assessment of forest fragmentation clearly depends on the scale of analysis. We examined one aspect of spatial scale (i.e., the window size), and the attribute scale (i.e., the definition of forest). As window size increases, forest areas shift from interior, perforated, and undetermined categories into edge, transitional, and patch categories. As the number of recognized forest types increases, more fragmentation is detected unless the particular forest type dominates the analysis
window (see Appendix 1).
Fragmentation measurements are also sensitive to pixel size. For
example, Nepstad et al. (1999a,b) [See Erratum.] reported higher fragmentation when using finer grain maps over a fixed extent (window size) of tropical rain forest. Finer grain maps identify more nonforest area where forest cover is dominant but not exclusive. Our results for interior forest in the same area indicate that for a fixed grain size, fragmentation is greater when maps of larger extent are used. The strict criterion for interior forest is more difficult to satisfy over larger areas.
The fragmentation model performed well in the mapping exercises, but could be improved. First, although knowledge of the feasible parameter space was not critical, there are geometric constraints (O’Neill et al. 1996; see Appendix 2). For example, it is not possible to obtain a low value of Pff when Pf is large. Second, percolation theory applies strictly to maps resulting from random processes; hence, the critical values of Pf (0.4 and 0.6) are only approximate and may vary with actual pattern. As a practical matter, when Pf > 0.6, nonforest types generally appeared as “islands” on a forest background, and when Pf < 0.4, forests appeared as “islands” on a nonforest
background. Finally, the undetermined category might be combined with another because it contains little area and is not readily interpretable with respect to fragmentation. However, a map of the undetermined category shows the locations where the actual pattern shifts from perforated to edge (e.g., Fig. 4 d,e), and such areas may be worth highlighting in some applications.
Our analysis does not distinguish between natural and anthropogenic fragmentation. For some ecosystem processes, the distinction does not matter, but knowing the causes of fragmentation in different places is essential for developing effective policies related to land use near forests. We were frustrated by a lack of independent, comparable-scale, global maps of potential vegetation (needed to quantify “natural” fragmentation) and human influence (needed to quantify “anthropogenic” fragmentation). For example, available global maps of potential vegetation (e.g., Leemans 1990) are coarser by two orders of magnitude in comparison to the land-cover maps. On such maps, “natural” fragmentation appears only on the margins of large forest masses, where temperature and moisture constrain vegetation to nonforest cover types. This may or may not reflect true patterns of potential vegetation at finer scales. Finer scale maps of potential vegetation and human influence zones are available for some countries and could be used to infer the cause of observed fragmentation in those countries. Comparisons among countries would then have to account for differences in the ancillary maps.
Some of the fragmentation that we detected on the land-cover maps is the result of excluding savanna and woody savanna from the forest class definition. If one chooses to include savanna in the definition of forest, then our fragmentation maps overestimate perforated and edge area and underestimate interior area in forest types such as boreal forests and tropical semideciduous woodland that contain large inclusions of savanna. Forests that are not located near savanna types are not affected. The definition of forest can have a large influence on the types and degree of fragmentation detected in any survey (see also Appendix 1).
When “anthropogenic” causes of fragmentation are considered, forests are more likely to be disturbed and fragmented where climate is hospitable, soil is productive, and access is easy. Boreal forests contain a high percentage of interior forest because the climate is not hospitable and access is poor. In contrast, nearly all of Europe and eastern North America are also naturally forested, but are more hospitable and accessible. Humans not only have converted large areas to nonforest uses, but also have created islands of nonforest cover in the otherwise interior regions of the residual forest.
Tropical rain forests remained relatively intact until access was made easier. In the Rondonia region, for example, the pattern of residual forest is directly related to the road pattern (Dale and Pearson 1997). In the Amazon Basin, there are corridors of fragmented forest that follow major rivers and other access routes into larger regions of interior forest. Because we considered water
pixels to be ‘missing’ data, the corridors are the result of nonforest cover types adjacent to rivers and not the river itself. The opposite pattern (with respect to rivers) is obtained in the southeastern part of North America, where overland access is easier and riparian zones contain more residual forest than upland zones.
The Appalachian Mountains in eastern North America contain the only extensive region of interior forest at middle latitudes. Until recently, this area was relatively undeveloped. Proposed mining operations will convert large forest tracts to grassland and will almost certainly reduce the amount of interior forest estimated from our model and the land-cover map that we used. At the
same time, large portions of the region are public lands where retention of forest cover is probable.
There is abundant evidence of perforated tropical rain forest, but fragmentation seems to have proceeded into patch status in only a small percentage of the overall rain forest area. Tropical rain forest in Europe–Asia has the highest percentage (42.1%) of interior conditions and the lowest percentage (24.1%) of perforated conditions. North America has the lowest percentage (25.1%) of interior and the highest percentage (44.8%) of perforated tropical rain forest area. These statistics are probably affected by the distinction drawn between “tropical rain forest” and “tropical degraded forests” on the Olsen maps.
In comparison to other forest types around the world, tropical rain forest may be at higher risk because of current land-use trends, but our analysis identifies other types that appear to be more heavily fragmented today. The deciduous broadleaf type has very low percentages (5 – 15%) of interior conditions, and occurs mainly in transitional and patch categories in Africa, and in perforated and edge conditions in Europe–Asia and North America. The cool conifer forest type exhibits similar patterns in Europe–Asia, but not in North America. In South America, the evergreen broadleaf forest, montane tropical forest, and cool southern hemisphere mixed forest types are mostly in transitional and patch categories, with very low percentages of interior conditions. In Africa, most dry evergreen woods are in transitional and patch categories.
The greatest impact of our study may be the model, not the particular results, although the results may merit consideration in international policy arenas. The impact will be greater because the model enables policy makers to change the way in which they think, not what they think. If it is important that policy considers spatial pattern in relation to land use or climate change, then policy makers require suitable tools to address the issues. Our model is a simple device to introduce pattern into a discussion that is now dominated by statistics on the amount of forest per unit area. One potentially useful feature of the model is that it can be collapsed into the one dimension of the amount of forest per unit area; most of the information about forest pattern would be lost as a result. Another potentially useful feature is that the model works in the same
way (although results will vary) for any raster of categories at any scale.
If it is practical to manage the large-area spatial arrangement of forests to achieve certain states of fragmentation, then a logical first question is where to do that. Because it is possible to make changes that are of no consequence in a regional setting, any plan has to consider the context of each candidate location and the scales over which pattern can actually be altered for a given
level of investment. Using our model, one strategy to identify large regions for preservation might be based on the persistence of interior conditions as window size increases. The model could also be used to evaluate restoration potential. For example, a strategy to expand the area of interior conditions might fill in the perforated regions. A strategy to reduce vulnerability might be focused on places that are near critical thresholds.
A second question is the purpose of managing fragmentation. Success in managing forest patterns will not necessarily result in successful ecosystem management. Different aspects of an ecosystem may be more or less sensitive to the same type or degree of fragmentation. Multiple-scale approaches are needed because no one scale can possibly apply to all of the ecosystem functions that are affected by fragmentation. Managing fragmentation might be considered a necessary, but not sufficient, condition for the maintenance of specific ecosystem functions that exhibit a response to fragmentation.
Our analysis places “patches” into perspective as one identifiable element along a continuum of forest fragmentation, and suggests that more attention should be given to perforated conditions. The research emphasis on “patches” comes from many sources, ranging from our abilities to visualize and delineate what they represent, to their usage as conceptual units in metapopulation and patch dynamics models, and to societal biases such as land ownership. However, consider the importance of patches in Rondonia, for example (Fig. 4). Here, the places that are the most likely to exhibit qualitative future changes are not in the region of existing patches, but rather are in the surrounding halo of perforated forest. Patches may become smaller and fewer in number, but they are still the same population of patches, and they occupy less than half of the total area. If history elsewhere is a guide, perforations in the halo will grow and coalesce, causing transitions that form entirely new populations of patches.
Responses to this article are invited. If accepted for publication, your response
will be hyperlinked to the article. To submit a comment, follow
this link. To read
comments already accepted, follow this link.
The research in this paper was funded by the U.S. Environmental Protection Agency through an Interagency Agreement with the U.S. Department of the Interior. The authors thank Tom Loveland, Roger Tankersley, and four anonymous reviewers for helpful comments. This work is dedicated to the memory of Vernon Riitters.
Bierregaard, R. O., T. E. Lovejoy, V. Kapos, A. A. dos Santos, and R. W. Hutchings.
1992. The biological dynamics of tropical rainforest fragments. BioScience
42:859-866.
Dale, V. H., and S. M. Pearson. 1997. Quantifying habitat fragmentation due
to land-use change in Amazonia. in W. F. Laurance and R. O. Bierregaard,
editors. Tropical forest remnants: ecology, management, and conservation of
fragmented communities. University of Chicago Press, Chicago, Illinois, USA.
Forman, R. T. T., and M. Godron. 1986. Landscape ecology. John Wiley,
New York, New York, USA.
Gustafson, E. J. 1998. Quantifying landscape spatial pattern: what is the state
of the art? Ecosystems 1:143-156.
Harris, L. D. 1984. The fragmented forest. Island biogeography theory and the preservation of biotic diversity. University of Chicago Press, Chicago, Illinois, USA.
Houghton, R. A. 1994. The worldwide extent of land-use change. BioScience 44:305-313.
Laurance, W. F., S. G. Laurance, and P. Delamonica. 1998. Tropical forest fragmentation
and greenhouse gas emissions. Forest Ecology and Management 110:173-180.
Laurance, W. F., S. G. Laurance, L. V. Ferreira, J. M. Rankin-de Merona, C. Gascon, and T. E. Lovejoy. 1997. Biomass collapse in Amazonian forest fragments. Science 278:1117-1118.
Leemans, R. 1990. Global data sets collected and compiled by the biosphere project. Working Paper, International Institute of Applied Systems Analysis, Laxenburg, Austria.
Levin, S. A. 1992. The problem of pattern and scale in ecology. Ecology 73:1943-1967.
Lovejoy, T. E., R. O. Bierregaard, A. B. Rylands, J. R. Malcolm, C. E. Quintela, L. H. Harper, K. S. Brown, A. H. Powell, G. V. N. Powell, H. O. R. Schubart, and M. B. Hays. 1986. Edge and other effects of isolation on Amazon forest fragments. In M. E. Soulé, editor. Conservation biology: the science of scarcity and diversity. Sinauer Associates, Sunderland, Massachusetts, USA.
Loveland, T. R., and A. S. Belward. 1997. The IGBP-DIS global 1 km land cover
data set, DISCover first results. International Journal of Remote Sensing 18:3289-3295.
Loveland, T. R., B. C. Reed, J. F. Brown, D. O. Ohlen, Z. Zhu, L. Yang, and J. W. Merchant. 1999. Development of a global land cover characteristics database and IGBP DISCover from 1-km AVHRR data. International Journal of Remote Sensing (in press).
Meyer, W. B., and B. L. Turner, II. 1994. Changes in land use and land cover: a global perspective. Cambridge University Press, Cambridge, UK.
Nepstad, D. C., P. Lefebvre, and E. A. Davidson. 1999a. Positive feedbacks in
the fire dynamic of closed canopy tropical forests. Science
284:1832-1835. [See Erratum.]
Nepstad, D. C., A. Verissimo, A. Alencar, C. Nobre, E. Lima,
P. Lefebvre, P. Schlesinger, C. Potter, P. Moutinho, E. Mendoza,
M. Cochrane, and V. Brooks. 1999b. Large-scale
impoverishment of Amazonian forests by logging and fire. Nature
98:505-508. [See Erratum.]
Olsen, J. S., and J. A. Watts. 1982. Major world ecosystems complex map. Oak
Ridge National Laboratory, Oak Ridge, Tennessee, USA.
O’Neill, R. V., C. T. Hunsaker, K. B. Jones, K. H. Riitters, J. D. Wickham, P. M. Schwartz, I. A. Goodman, B. L. Jackson, and W. S. Baillargeon. 1997. Monitoring environmental quality at the landscape scale. BioScience 47:513-519.
O’Neill, R. V., C. T. Hunsaker, S. P. Timmins, B. L. Jackson, K. B. Jones, K. H. Riitters, and J. D. Wickham. 1996. Scale problems in reporting landscape pattern at the regional scale. Landscape Ecology 11:169-180.
Riitters, K. H., R. V. O’Neill, and K. B. Jones. 1997. Assessing habitat
suitability at multiple scales: a landscape-level approach. Biological Conservation 81:191-202.
Skole, D., and C. Tucker. 1993. Tropical deforestation and habitat fragmentation in the Amazon: Satellite data from 1978 to 1988. Science 260:1905-1910.
Stauffer, D. 1985. Introduction to percolation theory. Taylor and Francis,
Philadelphia, Pennsylvania, USA.
Tucker, R. P., and J. F. Richards. 1983. Global deforestation and the nineteenth century world economy. Duke University Press, Durham, North Carolina, USA.
Turner, B. L. II, W. C. Clark, R. W. Kates, J. F. Richards, J. T. Mathews, and W. B. Meyer. 1990. The Earth as transformed by human action. Cambridge University Press, Cambridge, UK.
Turner, M. G. 1989. Landscape ecology: the effect of pattern on process. Annual
Review of Ecology and Systematics 20:171-197.
Turner, M. G., and R. H. Gardner, editors. 1991. Quantitative methods in landscape ecology. Springer-Verlag, New York, New York, USA.
Woodwell, G. M., R. A. Houghton, T. A. Stone, R. F. Nelson, and W. Kovalick. 1987. Deforestation in the tropics: new measurements in the Amazon Basin using Landsat and NOAA Advanced Very High Resolution Radiometer Imagery. Journal of Geophysical Research 92:2157-2163.
A comparison of pre- and post-stratifying land-cover maps for fragmentation analysis.
The feasible and realized parameter space for the analysis of forest fragmentation in South America at the 81-km2 scale.
Fig. 5. Global patterns of forest fragmentation within 81-km 2 windows. The pie chart indicates the percentage of total forest area in each fragmentation category.
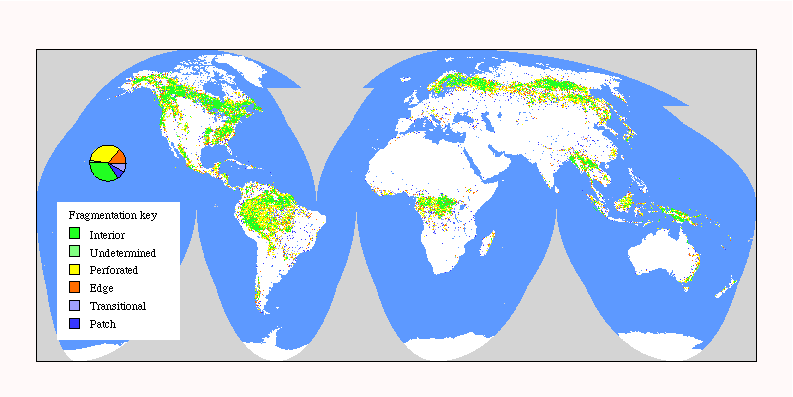
Fig. 6. Global patterns of forest fragmentation within 729-km 2 windows. The pie chart indicates the percentage of total forest area in each fragmentation category.
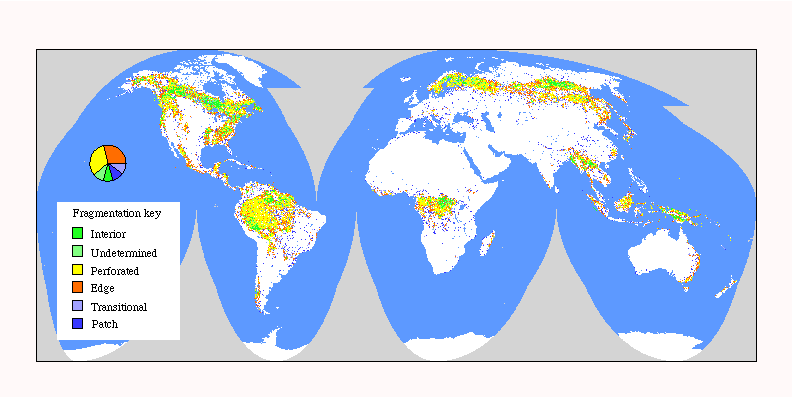
Fig. 7. Global patterns of forest fragmentation within 6561-km 2 windows. The pie chart indicates the percentage of total forest area in each fragmentation category.
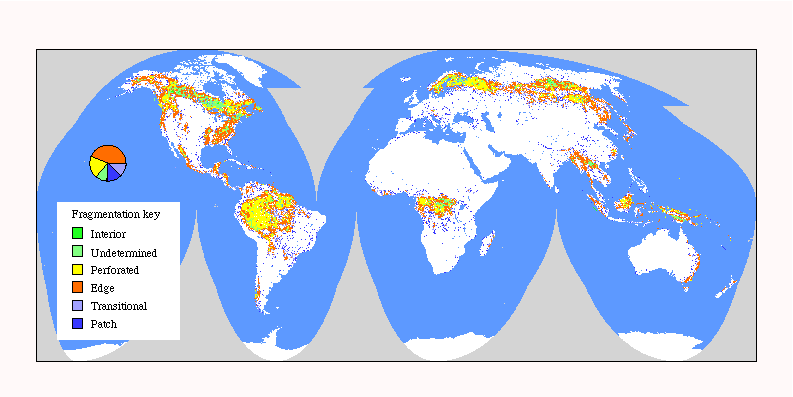
Fig. 8. Global patterns of forest fragmentation within 59049-km 2 windows. The pie chart indicates the percentage of total forest area in each fragmentation category.
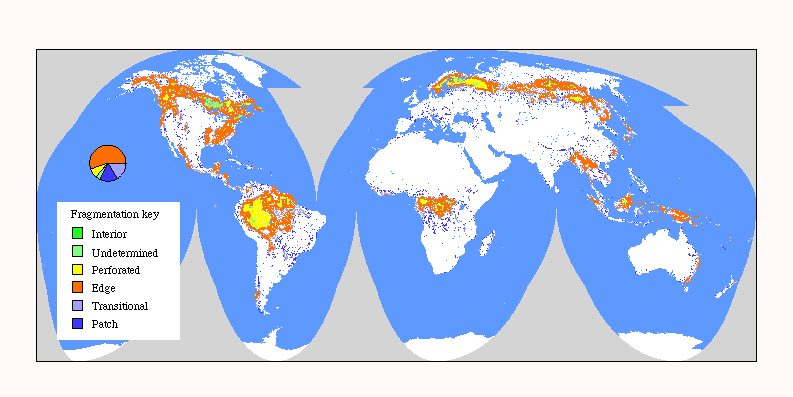
Fig. 9. Patterns of forest fragmentation within 81-km 2 windows for Africa. The pie chart indicates the percentage of continental forest area that is in each fragmentation category.
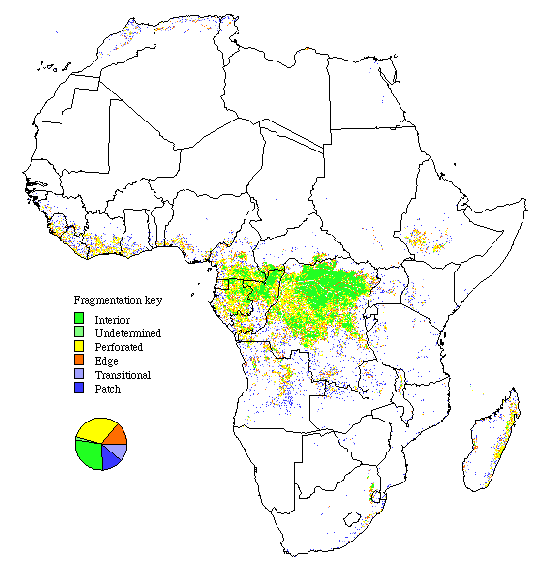
Fig. 11. Patterns of forest fragmentation within 81-km 2 windows for Europe–Asia. The pie chart indicates the percentage of continental forest area that is in each fragmentation category.
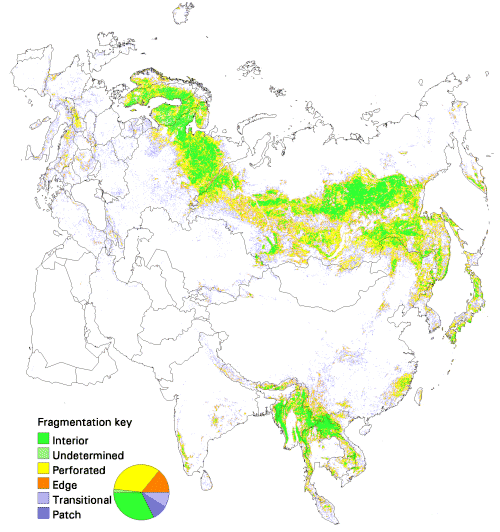
Fig. 12. Patterns of forest fragmentation within 81-km 2 windows for North America. The pie chart indicates the percentage of continental forest area that is in each fragmentation category.
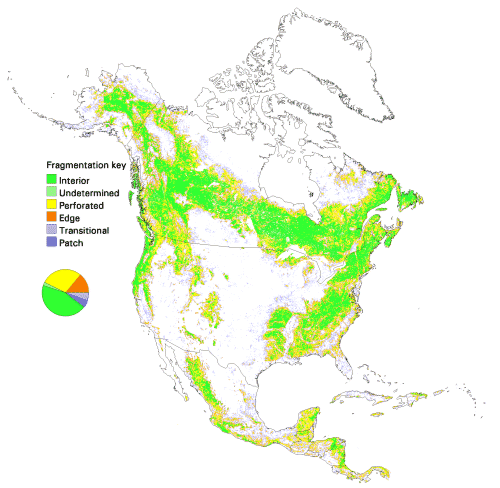
Fig. 13. Patterns of forest fragmentation within 81-km 2 windows for South America. The pie chart indicates the percentage of continental forest area that is in each fragmentation category.
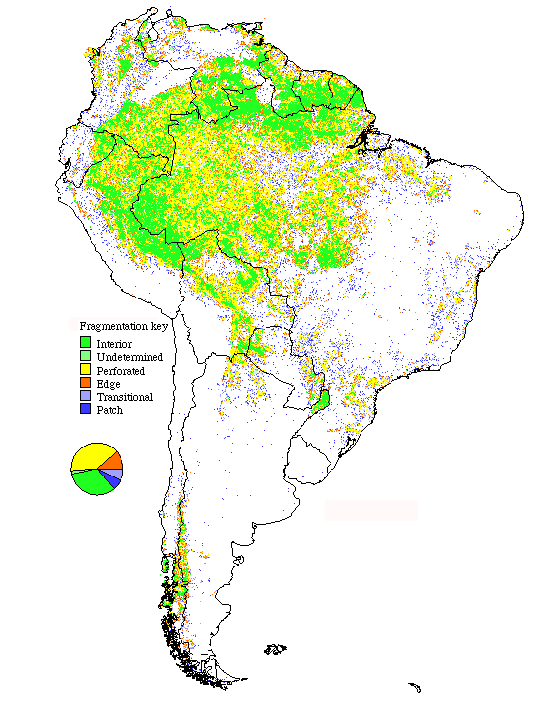
Table 1. Forest area and percentage of forest area in different fragmentation categories, by continent. The percentages in the table also appear in pie charts in Figs. 9–13.
Continent
Forest areaa
(103 km2)Percentage of continent forest area in fragmentation category
Interior
Undetermined
Perforated
Edge
Transitional
Patch
Africa
2732
28.7
1.9
31.8
13.9
11.1
12.7
Australia–Pacific
2135
27.1
2.2
35.1
16.1
10.9
8.7
Europe–Asia
9551
32.0
2.1
34.1
14.1
9.0
8.7
North America
8565
44.9
2.3
28.5
14.0
5.6
4.7
South America
6940
33.0
2.0
39.6
11.6
7.4
6.5
Table 2. Forest area and percentage of forest area in different fragmentation categories, by forest type and continent. Each row in the table has a map of the fragmentation categories for that forest type and continent (Figs. 14–66).
Olsen forest type
Continent
Forest
area a
(103 km2)Percentage of type total
Fig. no. (map)
Percentage of continent forest type total in fragmentation category
Interior
Undetermined
Perforated
Edge
Transitional
Patch
Coniferous
North America
24
100.0
14
66.2
2.2
21.3
9.1
0.7
0.6
Deciduous conifer
Europe–Asia
1961
100.0
15
43.7
1.9
30.8
11.5
6.3
5.8
Deciduous broadleaf
Africa
14
3.0
16
5.6
2.1
13.2
29.7
23.8
25.6
Europe–Asia
363
75.9
17
5.4
1.8
31.6
18.0
18.8
24.4
North America
101
21.1
18
14.9
2.2
39.7
20.3
12.2
10.7
Evergreen broadleaf
Australia–Pacific
64
65.0
19
19.4
2.7
31.4
21.9
11.5
13.1
South America
34
35.0
20
2.1
1.5
32.2
16.9
23.6
23.8
Cool rain
North America
98
100.0
21
67.7
2.2
19.7
7.9
0.5
2.0
Conifer boreal
Europe–Asia
1388
43.2
22
39.3
2.2
36.2
9.5
6.0
7.0
North America
1825
56.8
23
64.2
2.0
21.6
8.5
2.1
1.5
Cool conifer
Europe–Asia
166
12.0
24
4.2
1.3
26.4
14.2
18.7
35.2
North America
1215
88.0
25
37.1
2.3
33.2
15.0
6.4
5.9
Cool mixed
Europe–Asia
1192
58.5
26
20.0
2.6
43.2
18.1
9.6
6.4
North America
846
41.5
27
57.6
2.2
24.2
10.3
2.9
2.8
Mixed
Europe–Asia
627
59.4
28
22.9
1.9
27.4
17.5
14.6
15.7
North America
428
40.6
29
39.8
2.3
26.7
17.0
8.2
6.0
Olsen forest type
Continent
Forest
area a
(103 km2)Percentage of type total
Fig. no. (map)
Percentage of continent forest type total in fragmentation category
Interior
Undetermined
Perforated
Edge
Transitional
Patch
Cool broadleaf
Europe– Asia
266
32.5
30
7.5
1.7
28.1
17.6
20.7
24.5
North America
551
67.5
31
55.3
2.2
23.0
12.3
3.8
3.5
Deciduous broadleaf
North America
444
100.0
32
38.4
2.5
29.5
18.8
6.3
4.5
Conifer
Europe–Asia
125
17.3
33
10.1
2.4
43.0
18.7
14.2
11.6
North America
594
82.4
34
24.9
3.0
34.9
22.1
8.8
6.4
South America
2
0.3
35
6.7
3.2
18.7
46.3
17.4
7.8
Montane tropical
Africa
115
45.3
36
21.6
1.9
29.2
18.9
14.1
14.4
Australia–Pacific
23
8.9
37
35.1
2.1
34.4
15.1
8.5
4.8
South America
116
45.8
38
0.6
0.8
21.2
11.8
29.3
36.4
Seasonal tropical
Africa
867
65.7
39
36.3
1.9
26.4
14.6
9.3
11.5
Australia–Pacific
83
6.3
40
52.3
2.1
28.4
11.9
3.6
1.8
Europe–Asia
76
5.7
41
50.2
2.0
23.0
14.4
5.6
4.7
North America
86
6.5
42
26.7
2.3
45.2
13.6
7.0
5.1
South America
208
15.8
43
14.3
2.2
39.4
19.7
14.4
10.0
Dry tropical woods
North America
131
18.6
44
30.8
3.0
31.0
23.0
7.1
5.1
South America
571
81.4
45
9.3
1.6
30.2
16.1
19.3
23.6
Olsen
forest
typeContinent
Forest
area a
(103 km2)Percentage of type total
Fig. no. (map)
Percentage of continent forest type total in fragmentation category
Interior
Undetermined
Perforated
Edge
Transitional
Patch
Tropical
rainAfrica
1192
12.9
46
34.4
2.0
35.7
11.8
7.9
8.2
Australia–Pacific
1553
16.8
47
29.0
2.2
37.1
14.4
10.0
7.4
Europe–Asia
515
5.6
48
42.1
2.2
24.1
17.4
8.2
6.1
North America
220
2.4
49
25.1
2.7
44.8
16.6
7.4
3.4
South America
5793
62.5
50
37.2
2.1
41.2
10.4
5.3
3.9
Tropical degraded
Africa
1183
48.5
51
7.2
1.6
34.9
15.1
18.2
23.1
Europe–Asia
99
4.1
52
26.5
2.5
28.7
21.4
10.7
10.1
North America
51
2.1
53
7.7
2.2
53.0
18.5
12.2
6.4
South America
1108
45.4
54
5.2
1.8
44.4
15.3
18.3
14.9
Dry
evergreen woodsAfrica
138
44.9
55
0.4
1.3
22.1
20.8
29.8
25.5
Australia–Pacific
170
55.1
56
2.0
1.5
20.1
26.0
24.4
25.9
Cool S. hemi-
sphere mixedSouth America
38
100.0
57
2.1
1.6
24.9
26.9
25.1
19.5
Small-leaf mixed
Europe–Asia
877
48.3
58
15.0
2.3
37.2
20.3
12.9
12.4
North America
939
51.7
59
49.3
2.2
25.1
13.7
5.3
4.4
Deciduous and mixed
borealEurope–Asia
1808
100.0
60
25.9
2.2
40.5
14.2
9.2
8.0
Olsen forest
typeContinent
Forest
area a
(103 km2)Percentage of type total
Fig. no. (map)
Percentage of continent forest type total in fragmentation category
Interior
Undetermined
Perforated
Edge
Transitional
Patch
Narrow conifers
Europe– Asia
895
46.9
61
47.9
1.8
33.2
7.9
4.3
4.9
North America
1013
53.1
62
25.6
2.5
34.9
17.3
9.7
10.1
S. hemi-
sphere mixedAustralia–Pacific
48
27.3
63
7.5
1.8
34.2
16.6
20.6
19.3
South America
129
72.7
64
33.6
3.0
32.4
22.6
5.0
3.4
Moist eucalyptus
Australia–Pacific
195
100.0
65
28.9
3.0
37.1
20.7
7.1
3.3
Rain green tropical
Europe–Asia
414
100.0
66
27.5
2.2
25.6
22.9
12.2
9.6
Table 3. Percentage of the total area of five South American forest types, by fragmentation category, for two stratification rules and four window sizes. The percentages in the table also appear in pie charts in Figs. 67 through 71.
Olsen forest type
Stratificationa
Window size
( km2 )Percentage of continent forest type total in fragmentation category
Interior
Undetermined
Perforated
Edge
Transitional
Patch
Montane tropical
before
81
0.1
0.5
9.9
8.8
24.7
56.0
729
0.0
0.1
0.2
3.3
17.3
79.2
6561
0.0
0.0
0.0
0.0
1.9
98.1
59049
0.0
0.0
0.0
0.0
0.0
100.0
after
81
0.6
0.8
21.2
11.8
29.3
36.4
729
0.0
0.6
5.6
13.1
32.6
48.0
6561
0.0
0.2
0.8
16.7
33.7
48.7
59049
0.0
0.0
0.1
17.6
43.8
38.4
Seasonal tropical
before
81
10.1
1.6
22.8
19.0
19.3
27.1
729
1.7
2.3
5.2
24.3
24.1
42.3
6561
0.0
0.4
0.2
15.0
21.9
62.5
59049
0.0
0.0
0.0
0.6
11.9
87.5
after
81
14.3
2.2
39.4
19.7
14.4
10.0
729
2.2
3.6
20.7
35.4
22.8
15.4
6561
0.0
1.0
5.0
34.0
34.8
25.2
59049
0.0
0.0
0.9
11.6
38.2
49.2
Dry tropical woods
before
81
6.2
1.3
22.0
14.9
20.5
35.2
729
0.5
1.7
7.5
19.0
19.9
51.5
6561
0.0
0.3
0.6
14.2
16.0
68.9
59049
0.0
0.0
0.0
8.1
11.7
80.2
after
81
9.3
1.6
30.2
16.1
19.3
23.6
729
0.7
2.7
14.8
25.0
22.2
34.6
6561
0.0
0.9
2.7
26.8
24.7
44.9
59049
0.0
0.0
0.0
20.3
20.8
58.9
Tropical rain forest
before
81
35.9
2.1
40.6
10.9
5.6
4.9
729
7.3
9.2
47.2
22.9
7.0
6.5
6561
0.1
8.9
37.1
37.4
8.8
7.6
59049
0.0
5.1
22.4
51.7
12.1
8.7
after
81
37.2
2.1
41.2
10.4
5.3
3.9
729
7.7
9.5
49.1
22.0
6.7
5.0
6561
0.1
9.1
39.5
37.1
8.4
5.8
59049
0.0
4.6
24.0
53.8
10.9
6.7
S. hemisphere mixed
before
81
17.7
2.6
30.0
26.9
13.1
9.6
729
0.9
5.4
17.0
45.6
17.1
14.0
6561
0.0
2.3
11.7
40.0
23.9
22.1
59049
0.0
0.4
0.7
31.8
20.2
46.9
after
81
33.6
3.0
32.4
22.6
5.0
3.4
729
2.9
9.7
26.8
49.4
6.6
4.6
6561
0.0
3.0
16.6
64.7
9.6
6.2
59049
0.0
0.9
2.2
56.6
19.5
20.9