A4.1 Introduction

This model is an example of a system dynamics model and has four main components: sheep, hyrax (Procavia capensis Pallus), lynx (Felis caracal Schreber), and pasture. In section A4.2, I discuss traditional methods that have been used to solve and analyze such models. In section A4.3, I give some background and a few technical details needed to use XPPAUT for analyzing the dynamics. Section A4.5 contains the model analysis. I begin by studying the effects of various parameters and density-dependent functions on the behavior of the model. This analysis shows the limitations of a traditional sensitivity analysis and highlights dynamics that are biologically implausible, namely that pasture growth is unlimited when sheep densities are low. A modification to the pasture growth term is discussed in section A4.5.4. The quantity of most interest to farmers is revenue. A two-parameter study of the effects of culling rates on farmers' revenue completes the analysis. This is followed by section A4.6, which interprets the main results from a biological viewpoint.

A4.2 Dynamic models and systems analysis: some background

The systems approach to modeling was made popular by Forrester in the early 1960s (Forrester 1961). This approach involves dividing a system into a large number of very simple unit components (Watt 1966) and then using equations to describe the processes affecting each of these components. The methodology was originally applied to industrial, urban, and world population systems, but its utility has been extended to ecological applications by a number of researchers (e.g., Watt 1966, Jeffers 1978). A variety of aspects, such as age structure, developmental rates, and density-dependent relationships, can be included explicitly, thus increasing the realism of the model. Kowal (1971) notes that an analysis of dynamic models can provide approximations to ecosystem dynamics long before traditional experimental approaches can provide more detailed conclusions. Insights can also be obtained into aspects of the system that may otherwise be obscured by its complexity. However, dynamic models usually involve many equations (generally ordinary differential equations) and parameters, making their behavior difficult to predict (Patten 1971).

Traditionally, numerical routines have been used to obtain solutions over time for a given set of parameter values. Optimization routines are also often employed (Maynard Smith 1974) to determine the "best" possible strategy with respect to a cost or revenue function. These routines are implemented using computers (see Patten 1971, Gerald and Wheatley 1989, Hultquist 1988).

Although these methods are useful, their results depend on the particular parameter set used. Hadamard (1952) notes that since data in nature are never fixed, a mathematical model cannot be considered as corresponding to a physical phenomenon unless small variations in the parameter values lead to small changes in the solution given by the model. Attempts to heed this caveat have been based on the ideas of Tomovic (1963), and are often referred to as sensitivity analyses. These involve changing the values of the input variables and parameter values by a small amount (say 1% or 10%) and seeing whether these changes produce large or small variations in the performance of the model (Brylinsky 1972, Jeffers 1978). A sensitivity analysis does give some idea of the robustness of model predictions, but the information is limited in that only a single, small perturbation of each parameter is considered. (A method for perturbing a combination of parameters in order to find a "worst" case has been proposed by Hearne (1987), but it is not yet commonly used.) The dynamical systems techniques show the effects of a whole range of parameter values on the system.

A4.3 Model equations

Swart and Hearne (1989) developed a dynamic model to study the impact of hyrax (Procavia capensis Pallas) and lynx (Felis caracal Schreber) on sheep farming in a region in South Africa. Two main problems were identified. The first involves competition for pasture between hyrax and sheep; hyrax encroach on farm land when the hyrax population exceeds the carrying capacity of wilderness areas in the region. The second problem is the predation on sheep by lynx. The principal food for lynx is hyrax, but lynx prey on sheep from time to time. The latter problem is of direct concern to farmers; they tend to be more tolerant of the competition with hyrax.

Swart and Hearne (1989) developed their model to increase understanding of problems caused by the spillover of hyrax and lynx from their predator-prey system into the sheep-pasture system, and to determine the effects of different culling strategies for hyrax and lynx. There are 10 state variables in the model. The sheep, hyrax, and lynx populations are each divided into three classes: juveniles, female adults, and male adults. There is one variable representing pasture. The quantity of most interest to farmers is revenue. This auxiliary variable is a function of the state variables and is made up of wool sales, mutton sales, the value of sheep stock, and the cost of culling hyrax and lynx.

Swart and Hearne (1989) used optimization routines to find the hyrax and lynx culling rates that gave maximum profitability in terms of revenue. They also investigated the system's sensitivity to parameter perturbations. They found that lynx culling is essential and that substantial increases in both sheep numbers and revenue are possible by simultaneously culling hyrax and lynx. Optimal culling rates, in terms of revenue, are ~ 30% per annum for both hyrax and lynx. From a policy point of view, the model is robust with respect to small parameter variations.

My purpose is not to redo the work done by Swart and Hearne (1989), whosemodel and analysis have accomplished their aims. Instead, I want to illustrate the usefulness of the dynamical systems software in this setting.

A4.4 Technical details

A few minor modifications to the model are required to facilitate the use of this software. The first involves scaling the state variables so that they all have the same order of magnitude. Combining quantities of very different magnitude may lead to computer round-off errors (Gerald and Wheatley 1989). I chose values close to the initial values in Swart and Hearne (1989) as scaling constants s_i (see A4.7).

Secondly, in order for the computer packages to generate continuous bifurcation diagrams, all functions in the model need to be continuous. The original model uses two step functions to represent farmers' sheep-culling strategies. I replaced these with continuous functions having steep slopes in the region of the step.

In the original model, pasture production and fecundity rates vary seasonally. Since this complicates the dynamics considerably when it comes to parameter studies, and since the present study is more concerned with long-term equilibrium behavior than with day-to-day variations, I did not include the seasonality functions. Solving the system of equations numerically over time is still the best way to study seasonal variation, in most cases.

The various versions of AUTO only allow a state variable, or the L₂-norm of the state variables, to be displayed on the y -axis of the bifurcation diagrams they generate. The L₂-norm of a vector v = (v₁, ... , v_m) is given by

In order to have direct access to revenue values, it would be most convenient if revenue were a state variable. The following suggestion by Bard Ermentrout makes this possible.

Let v be the vector of existing state variables and let h(v) be the revenue function. We can add to the original system the equation

,

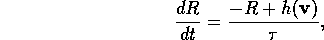where is a small parameter. R is the variable that we want to represent revenue. This ordinary differential equation will not affect system equilibria because, at these points, R = h(v) and, hence, dR/dt = 0 (as required for an equilibrium value). The existence and stability of phenomena such as periodic orbits (limit cycles) are also not affected. Since acts as a delay time, we would like it to be small so that R is a close approximation to revenue. However, care must be taken in the choice of , because very small values can give rise to computer truncation errors. For the current problem, = 0.05 was used.

A4.5 Model analysis

A4.5.1 Reference parameter values

A value of 0.35 for H_CN was optimal (in terms of revenue) for all values of L_CN. I chose this value for H_CN and then used XPPAUT to vary L_CN in order to find the corresponding optimal value for L_CN. The result was L_CN = 0.15.

A4.5.2 The effects of culling sheep

Note that AUTO encounters points beyond which it cannot calculate: S_FCN=0.54 is such a point. Using XPPAUT to solve the system of equations numerically for parameter values on either side of this limiting point, we can determine the causes of the difficulties. Output from a numerical integration is shown in XPPAUT's data window, and from this we see that the sheep population dies out for S_FCN >0.54. Beyond the limiting value, there is no equilibrium at which all three populations are present and, hence, AUTO cannot continue the equilibrium branch any further.

A second observation can be made by looking at the bifurcation diagram for pasture in Fig. 20. As the equilibrium number of sheep declines (as S_FCN increases and approaches the value corresponding to sheep extinction), the equilibrium value for pasture increases rapidly (and AUTO encounters numerical difficulties). Clearly, this is unrealistic and suggests that some modification should be made to the model equations to limit pasture growth. I return to this in section A4.5.4. Before modifying the equations to limit pasture growth, it is informative to study the roles of the existing density-dependent functions. This can be viewed as another form of sensitivity analysis, in which we investigate the system's response to whole functions instead of single parameters.

A4.5.3 The effects of density dependence

dP/dt = pasture production - pasture grazing = A.P_PN - T_SSU.G_N.G_M(P_A),

whereAis the area of the farming region under study; P_PN is the pasture production normal (average pasture growth rate); T_SSU is total small stock units (a representative value for the number of sheep); G_N is the grazing normal (average amount of pasture grazed per unit stock); and G_M is the grazing multiplier, which is a function of P_A, the pasture availability index. P_A is given by 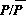, where P is an average pasture density. The grazing multiplier is an increasing function of P_A, which reaches a maximum of 1.5 around P_A = 3 and has a value of 1 at P_A = 1.

To remove a density-dependent function from the model, the simplest approach is to replace it by a constant function. For example, we can set G_M equivalent to 1. This was done for each multiplier function in turn, and bifurcation diagrams obtained from the altered model were compared with those from the original model in each case.

Removing the grazing multiplier, G_M, had the greatest effect on model dynamics. Even after I altered a number of parameter values, the system did not reach equilibrium. The sheep population either increased indefinitely or decreased to extinction for each parameter set that was tried. This is not surprising, since the grazing multiplier affects pasture grazing and sheep fecundity as well as sheep juvenile deaths. Without G_M, the density dependence of pasture grazing and sheep dynamics on pasture availability ( G_M is a function of P_A) is removed. The results show that this density dependence is critical for regulating the sheep-pasture subsystem.

The effects of the other functions in the model were quantitative rather than qualitative. That is, removing them from the model tended to decrease the range of parameter values over which sheep, hyrax, and lynx coexist at equilibrium, but did not alter the qualitative dynamics. This does not imply that these other functions play an insignificant role in the model. They have a regulatory effect and reduce the impact of parameter changes on model behavior. This resilience to disturbances is very desirable (Holling 1973) and is expected of many natural systems. I observed earlier that the model lacks a feedback relationship that would limit pasture growth when sheep densities are very low. Also, pasture availability has a significant influence on pasture grazing and sheep fecundity and, hence, on the predictions of the model. In the next section, Eq. A4.1 is modified to include density-dependent growth.

A4.5.4 Adding density dependence to pasture growth

dP/dt = pasture production - pasture grazing = A.P_PN.P_M(P_A) - T_SSU.G_N.G_M(P_A),

where P_M is a function of pasture availability, P_A. For high values of P_A, we expect pasture growth to slow down and saturate. We also expect a decline in growth when P_A is very low. A function having this general form is the Ricker function (see Fig. 21 ).

To test the effects of this new function, I generated a number of bifurcation diagrams and compared them with those from the original model. Figure 22 shows those diagrams that correspond to Fig. 20.

In Fig. 22a, total revenue declines to zero as S_FCN increases. This is more mathematically satisfactory than Fig. 20a, where the curve stops abruptly at a positive revenue value, because it indicates clearly where a positive sheep population is no longer possible. Figure 22c shows the maximum pasture density that occurs when a positive sheep equilibrium (and hence, a positive value for revenue) is impossible. This density is lower than in Fig. 20c, but depends on the exact nature of the pasture multiplier.

Another observation from Fig. 22 is that, instead of AUTO being unable to converge at very low S_FCN (sheep female culling normal) values, a Hopf bifurcation occurs, and the bifurcation diagrams show that no stable equilibrium at which all three populations coexist is possible for S_FCN < 0.059. For these values, there is insufficient pasture to support the high sheep population. Thus, introducing the pasture multiplier has improved the dynamics at low values of S_FCN as well as high values, and has solved the problem of revenue increasing rapidly as in Fig. 20a.

Using XPPAUT to integrate the system numerically gives insight into the dynamics corresponding to the different regions in the bifurcation diagrams. In particular, the temporal dynamics show that the pasture multiplier slows and limits pasture growth as desired. Comparing the dynamics of the original and modified models at S_FCN = 0.5 shows that limiting pasture growth has a stabilizing influence on the dynamics (see Fig. 23 ). The oscillatory approach to equilibrium by the original model (Fig. 23a) is replaced by a smooth approach in Fig. 23b.

The limiting value for pasture in Fig. 22c is still rather high, but I had no experimental data on which to base the form of the pasture multiplier, and did not think it worthwhile to fiddle with the function to obtain a more plausible value. Effects of introducing the multiplier have been adequately demonstrated already.

A closer look at the behavior of the model may suggest further modifications of the equations. I have shown just one example of how bifurcation diagrams can help in the process of model building. The next section describes how two-parameter studies can be used to obtain useful summaries of model behavior.

A4.5.5 A summary of the effects of culling both hyrax and lynx

Using the modified model, the bifurcation diagrams for the lynx culling normal L_CN have the form shown in Fig. 24 . For L_CN below the limit point, the sheep population dies out under too much predation by lynx. Using AUTO, the limit point can be continued in H_CN, the hyrax culling normal, as well as L_CN. That is, we can see how the position of this limit point varies as a function of both H_CN and L_CN. This gives the two-parameter bifurcation diagram in Fig. 25 . From this figure, it can be seen that sheep become extinct as a result of the combined effect of lynx predation and competition with hyrax for pasture, since both L_CN and H_CNare low in the region where sheep die out.

If Fig. 25 is combined with the observation that the lynx population dies out for L_CN ~> 0.37 for all values of H_CN, the result is Fig. 26 . This observation was made by generating bifurcation diagrams for L_CN for a number of different (fixed) H_CN values. Conversely, varying H_CN for a variety of fixed L_CN values does not produce any parameter ranges where the hyrax population dies out.

Figure 26 shows that all three populations coexist at equilibrium for a large set of culling rates. The diagram would be of even greater use if the revenue value corresponding to each point in this two parameter space were known. This can be done by recording information given by XPPAUT and using some other graphics package to plot a three-dimensional surface.

Using the modified model developed in the previous section, I fixed the value of H_CN, chose L_CN = 0.15 (say), and used XPPAUT to find the equilibrium point numerically. I then used the AUTO interface to vary L_CN in both directions. Using the GRAB feature of XPPAUT to move along the branch of equilibrium points, I recorded the revenue values at regular intervals along the curve. I did this for a number of H_CN values and plotted the results using the public domain graphics package GNUPLOT (Williams and Kelley 1986). A surface plot and corresponding contour plot are shown in Fig. 27 . As can be seen from the figure, there is a large region of parameter space over which revenue does not vary much, indicating that the model is very robust to changes in the culling rates in this region. This is a desirable property when it comes to developing management strategies.

A4.6 Conclusions

The analysis of the previous sections has led to a number of insights into the sheep-pasture-hyrax-lynx system. Figure 22 shows that altering the number of ewes that are culled only affects the sheep-pasture subsystem. However, the effects on this subsystem are considerable. Culling too many ewes will obviously cause sheep numbers to decline. More important is the effect on revenue. Significant increases in revenue are possible if the farmer culls fewer ewes, because there is a greater return if these sheep are allowed to reproduce than if they are taken to market (provided that the sheep stock is not too large for the pasture to support it, i.e., provided S_FCN > 0.059.) However, there is a trade-off: culling fewer ewes results in a lower cash flow. Another trade-off results from the decrease in pasture availability that accompanies a larger sheep stock. This is already reflected in the model by the dependence of sheep fecundity on pasture availability. However, an additional quantity representing the quality of sheep may be useful, as this will affect the returns from wool and mutton sales and, hence, revenue. This presents another opportunity for improving the model.

In section A4.5.3, I showed that density dependence of sheep and pasture dynamics on pasture availability is critical for regulating the sheep-pasture subsystem. In fact, this encouraged me to modify pasture growth to include density dependence. This modification restricts both pasture and revenue values from increasing indefinitely (compare Figs. 20 and 22) and also stabilizes the temporal dynamics (see Fig. 23). Other modifications, such as including the effects of hyrax grazing in the pasture equation, can also be made. In the interests of space, I have not discussed such a modification, but the approach in preceding sections indicates how such a modification can be introduced and studied.

Finally, the effects of culling both hyrax and lynx were summarized using two-parameter diagrams. In particular, Fig. 27 shows that the model is robust to changes in culling rates, provided that these rates are sufficiently high.

A4.7 Mathematical details for the sheep-hyrax-lynx model

A4.7.1 Modelling delays in system dynamics models

To represent this in the model, I use averaged or smoothed versions of certain quantities to calculate growth rates. Three quantities are averaged in this model: hyrax density (H_D), prey abundance (A_P), and the grazing multiplier (G_M). Sheep fecundity and juvenile mortality are functions of the grazing multiplier average, 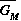_, instead of G_M. I use a first-order distributed delay (May 1973, MacDonald 1978) to calculate the averaged version, e.g.,

d /dt = ( 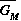) /t_del,

where t_del is the average delay time. Examples of this type of delay equation are found in Forrester (1961). MacDonald (1978) provides a detailed explanation of the mathematics underlying this differential equation. This ordinary differential equation is added to the original system of model equations, thus increasing the dimension of the system to be solved. Fortunately, this increase in dimension does not pose a problem when solving the system numerically.

Further discussions of delays in biological systems and their effects on system behavior are found in May (1973) and MacDonald (1989). For the sheep-hyrax-lynx model, the delays did not affect stability, even for large average delay times.

A4.7.2 Rescaling model equations

dv_i/dt = f_i(v₁, ... , v_i, ... , v_m).

Let v_i = s_i 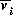, then

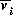= v_i/s_i

and

d 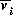/dt = (1/s_i)(dv_i/dt)= (1/s_i)f_i(s₁ 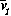, ... ,s_i 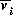, ... , s_m ).

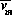Dropping the bars for convenience, we get

dv_i/dt = (1/s_i)f_i(s₁v₁, ... ,s_iv_i, ... , s_mv_m),

as required. The state variables have been replaced by s_iv_i and the differential equation for v_i is divided through by s_i, as stated in section A4.4.