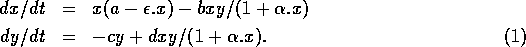
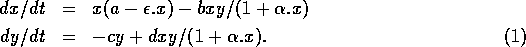
(see Appendix 2) are summarized in the two-parameter bifurcation
diagram in Fig. 16. This figure shows three regions in 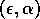 -parameter space, each
corresponding to a different form of qualitative behavior. In region
(i), there is a spiral attractor (say A) at which both x
and y are nonzero, as well as a saddle point (say B) on
the x -axis to the right of A. In region (ii), A is an
unstable source surrounded by a stable limit cycle and B is still a
saddle point on the x -axis. In region (iii), B is now
the attractor and A is a saddle point, but A has moved into the fourth
quadrant.
-parameter space, each
corresponding to a different form of qualitative behavior. In region
(i), there is a spiral attractor (say A) at which both x
and y are nonzero, as well as a saddle point (say B) on
the x -axis to the right of A. In region (ii), A is an
unstable source surrounded by a stable limit cycle and B is still a
saddle point on the x -axis. In region (iii), B is now
the attractor and A is a saddle point, but A has moved into the fourth
quadrant.
Since A and B exchange stability in crossing from regions (i) and (ii) to region (iii), we expect a transcritical bifurcation to occur as the line with negative slope in Fig. 16 is crossed from regions (i) and (ii) into region (iii). In crossing from region (i) to region (ii), point A changes from stable to unstable and a limit cycle is initiated. Thus, we expect a curve of Hopf bifurcations to divide these regions.
I used XPPAUT to reproduce Bazykin's results. (A comprehensive, interactive tutorial on how to use XPPAUT is available on the World Wide Web at the address
ftp://mthbard.math.pitt.edu/pub/bardware/xpptut/start.html.
The tutorial can also be obtained via anonymous ftp from
ftp.math.pitt.edu in the directory pub/bardware). The
required driving program containing the model equations and parameter
values is shown at the end of this appendix A3.1. As can be seen, it
is very straightforward. In order to use AUTO to create a bifurcation
diagram, we need a starting point that must be an equilibrium
point. By choosing values of 0.3 for 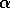 and 0.1 for
and 0.1 for  , we can either determine such a point
analytically (as Bazykin did), or we can use XPPAUT to perform the
task numerically.
, we can either determine such a point
analytically (as Bazykin did), or we can use XPPAUT to perform the
task numerically.
I then used AUTO to vary  . AUTO locates a transcritical
bifurcation (see Appendix 2) at
. AUTO locates a transcritical
bifurcation (see Appendix 2) at 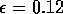 and a Hopf bifurcation at
and a Hopf bifurcation at 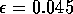 , together with stable
limit cycles (see Fig. 17). Since
, together with stable
limit cycles (see Fig. 17). Since 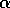 is fixed in Fig. 17, this
one-parameter diagram describes the dynamics along a horizontal line
at, say,
is fixed in Fig. 17, this
one-parameter diagram describes the dynamics along a horizontal line
at, say, 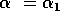 in
Fig. 16.
in
Fig. 16.
In Fig. 17, I have labeled the continuation branches A and B to
indicate which equilibrium point corresponds to which branch (see
Appendix 2 for a description of a continuation branch). Notice that
the x -coordinate of A does not vary with  , but the x
-coordinate of B does. The analytical forms of the equilibrium
points, which are given by
, but the x
-coordinate of B does. The analytical forms of the equilibrium
points, which are given by
These are obtained by setting the right-hand sides in the
predator-prey equations (see Eqs. A2.1) equal to zero and solving for
x and y. As expected,  does not appear in the x
-coordinate for A, but does appear in that for B.
does not appear in the x
-coordinate for A, but does appear in that for B.
In the range 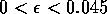 , point
A is unstable and B is a saddle point (see Appendix 2). There is also
a stable limit cycle surrounding A. Hence, these values of
, point
A is unstable and B is a saddle point (see Appendix 2). There is also
a stable limit cycle surrounding A. Hence, these values of  correspond to region
(ii) in Fig. 16. For
correspond to region
(ii) in Fig. 16. For 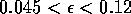 , A is a stable equilibrium point and
B is again a saddle point. This configuration corresponds to region
(i) in Fig. 16. For
, A is a stable equilibrium point and
B is again a saddle point. This configuration corresponds to region
(i) in Fig. 16. For 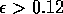 , B is now stable and A is a saddle
point, but the numerical output from AUTO shows that the y
-coordinate for A is negative for these values of
, B is now stable and A is a saddle
point, but the numerical output from AUTO shows that the y
-coordinate for A is negative for these values of  . This corresponds to
region (iii) in Fig. 16.
. This corresponds to
region (iii) in Fig. 16.
AUTO can be used to continue the Hopf bifurcation at
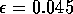 in
in
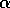 as well as
as well as
 , resulting in a two-parameter bifurcation diagram. This is shown in
Fig. 18
.
, resulting in a two-parameter bifurcation diagram. This is shown in
Fig. 18
.
Note that the curve of Hopf bifurcations is very different from
Bazykin's straight line in Fig. 16. I will return to this point
shortly. A second observation is that, for the given values of
a, b, c, and d , a Hopf bifurcation (and
hence limit cycle behavior) is only possible if 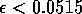 and
and 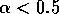 , which is a fairly small region of
parameter space and, hence, probably not of much biological
significance. (AUTO slows down considerably as
, which is a fairly small region of
parameter space and, hence, probably not of much biological
significance. (AUTO slows down considerably as 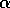 increases toward 0.5 and
increases toward 0.5 and  tends to 0 and never
actually reaches this point, although the curve does get very close if
AUTO is left to run for a sufficiently long time period. It can be
verified analytically that the curve does pass through
(0,0.5). However, complex behavioral changes occur at this point,
which is why AUTO has computational difficulties.)
tends to 0 and never
actually reaches this point, although the curve does get very close if
AUTO is left to run for a sufficiently long time period. It can be
verified analytically that the curve does pass through
(0,0.5). However, complex behavioral changes occur at this point,
which is why AUTO has computational difficulties.)
It is not possible to continue transcritical bifurcations in two
parameters using AUTO, as they are structurally unstable unless the
system possesses intrinsic symmetry. However, if 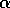 is fixed at a number of different
values and one-parameter bifurcation diagrams similar to Fig. 17 are
created by varying
is fixed at a number of different
values and one-parameter bifurcation diagrams similar to Fig. 17 are
created by varying  in each case, then the values corresponding to transcritical
bifurcations can be recorded. An approximation to the two-parameter
curve can then be drawn through these points. Figure 19
shows the resulting curve, together with the Hopf bifurcation continuation.
in each case, then the values corresponding to transcritical
bifurcations can be recorded. An approximation to the two-parameter
curve can then be drawn through these points. Figure 19
shows the resulting curve, together with the Hopf bifurcation continuation.
Bazykin's model is simple enough that the curves in Fig. 19 can be determined analytically, although the algebraic manipulations are rather tedious. It can be shown that transcritical bifurcations occur along the straight line
 ,
,
and Hopf bifurcations occur along the curve
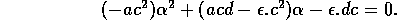
(A description of the methods involved in calculating these curves can be found in Guckenheimer and Holmes (1983) or Wiggins (1990). I used MAPLE (Waterloo Maple Software 1990-1992) for some of the algebraic manipulations. I have only included these expressions here to show the accuracy of AUTO's results. The availability of packages such as AUTO precludes the need for the reader to perform such mathematical manipulations.) These are exactly the curves shown in Fig. 19. Hence, AUTO's results are more accurate than Bazykin's linear approximation (Fig. 16) for the Hopf bifurcation curve. The new regions (i), (ii), and (iii) are shown in Fig. 19. XPPAUT or DSTOOL can be used to obtain phase portraits and time plots corresponding to different parameter combinations in Fig. 19. Due to space considerations, I have not included any such diagrams here. Time plots are useful for indicating the speed with which the stable equilibrium or limit cycle is attained and the period of the limit cycle, if applicable. If a system takes a long time to approach an attractor, then the transient dynamics may be of greater practical importance than the long-term behavior.
This section has shown how to rederive Bazykin's work (1974) on the system of Eqs. A2. more accurately and without having to completely understand the mathematical techniques involved. It has also established some confidence in AUTO's results.