APPENDIX 2
DYNAMICAL SYSTEMS BASICS
A2.1 Glossary of dynamical systems terminology
This appendix lists alphabetically those topics that are required in the main body of the paper and in the appendices. Brief descriptions are given and diagrams are used to explain the concepts as simply and intuitively as possible. A more comprehensive introduction to dynamical systems theory can be found in most introductory dynamical systems texts (e.g., Guckenheimer and Holmes 1983, Seydel 1988). Yodzis (1989) explains the theory using ecological examples, and Strogatz (1994) gives an informal introduction to nonlinear dynamics, with an emphasis on geometric intuition and scientific applications.
A2.1.1 Bifurcation diagram
A one-parameter bifurcation diagram summarizes the qualitative behavior corresponding to different values of a parameter. A state variable, or some function of the state variables, is usually plotted on the y -axis and the parameter on the x -axis. The positions and local stabilities of equilibrium points, as well as periodic orbits, are indicated using different line types. Solid curves are used to represent locally stable equilibria and dotted curves are used for locally unstable equilibria. Maxima and minima of periodic orbits are indicated using circles: solid for stable orbits and open for unstable orbits.
It is important to note that bifurcation diagrams summarize the behavior associated with a range of parameter values. They do not represent the dynamics corresponding to a continually varying parameter (Wiggins 1990). To read a bifurcation diagram, fix the parameter at a particular value and mentally draw a vertical line at that value. Each crossing of this line with a curve in the diagram corresponds to an equilibrium point or a periodic orbit (limit cycle). The local stability properties of a particular phenomenon are given by the type of curve: solid, dotted, or open or closed circles. For example, the phase portraits in Fig. 14b
(i) and (ii) were obtained by mentally drawing vertical lines at the parameter values
µ =
µ1
and
µ =
µ2,
respectively, in Fig. 14a.
A two-parameter bifurcation diagram shows how the positions of bifurcation points change as two parameters are varied. For example, if a bifurcation point is encountered in a one-parameter bifurcation diagram, a second parameter may be varied to see how it affects the position of the bifurcation point. An example is shown in Fig. 19.
A2.1.2 Bifurcation point
A bifurcation point is a point in parameter space at which the qualitative behavior of the system changes. A stable equilibrium may become unstable at this point, or there may be a change from a stable equilibrium to oscillatory behavior. Examples can be found in sections A2.1.6, A2.1.8, A2.1.11, and A2.1.19.
A2.1.3 Continuation branch
A solution branch, or continuation branch, is a curve of equilibrium points (or limit cycles or bifurcation points) that indicates how the position and properties of the equilibrium point (or limit cycle or bifurcation point) change as a parameter (or parameters) is altered. Together, a number of these branches make up a bifurcation diagram.
A2.1.4 Domain of attraction
Suppose the system in which we are interested has a stable equilibrium point (see section A2.1.9). Then the collection of all initial state variable values from which the system tends toward this equilibrium, as time progresses, is the domain (or basin) of attraction of the equilibrium point. The equilibrium point is called an "attractor." Any stable phenomenon, such as a stable limit cycle, also has a domain of attraction and is referred to as an attractor.
A2.1.5 Hard loss of stability
In the case of a Hopf bifurcation, this occurs when there is a rapid change from stable equilibrium behavior to stable limit cycles of large amplitude. This results from a subcritical Hopf bifurcation in which the unstable orbit reaches a limit point and turns around to stabilize. An example is shown in
Fig. 12. When the parameter
µ
is increased beyond the Hopf bifurcation at
µ*,
the system rapidly changes to limit cycles of large amplitude instead of starting off with small limit cycles that grow in size as
µ
increases, as shown in
Fig.15
. Also, as
µ
is decreased,there is a jump from large-amplitude cycles to a zero-amplitude equilibrium point, but this takes place at
µ1,
which is less than
µ*.
For
µ1 <
µ <
µ*,
there are two stable attractors, an equilibrium point and a limit cycle. Examples of hard loss of stability arise in the analysis of the ratio-dependent model.
A2.1.6 Hopf bifurcation
A Hopf bifurcation (also known as a Poincaré-Andronov-Hopf bifurcation; Arnold 1983, Wiggins 1990) is a bifurcation point at which an equilibrium point alters stability and a limit cycle (period orbit) is initiated. The example in Fig. 15 has a stable limit cycle surrounding an unstable equilibrium point. It is also possible to have an unstable limit cycle encircling a locally stable equilibrium point. Unstable periodic orbits are indicated by open rather than solid circles.
A2.1.7 Limit cycle
(See periodic orbit, section A2.12)
A2.1.8 Limit point
A limit point or saddle-node bifurcation occurs when there are two equilibrium points on one side of the bifurcation point, but none on the other side.
Figure 13a
shows an example of a bifurcation diagram of a limit point (LP). For
µ <
µ*,
there are no equilibrium points at which both populations are nonzero.
µ*
is thus the limiting value of
µ
for which equilibrium points exist; hence, the name limit point. A possible phase portrait in two dimensions for
µ >
µ*
is shown in Fig. 13b for the particular value
µ =
µ1.
A is a locally stable equilibrium point and B is a saddle point. The initial values of x1 and x2 determine the subsequent behavior of the system. If the initial point is in the domain of attraction of A (to the right of point B in Fig. 13b), then the system will approach A. However, if the initial point lies on the other side of B, it will be repelled away from B in the opposite direction to A. Notice how the size of the domain of attraction of A, in terms of the state variable x1, decreases as
µ
decreases towards
µ*
(see Fig. 13a).
A2.1.9 Local stability
Suppose the system in which we are interested is disturbed slightly from its equilibrium point. For example, a week of warmer weather may cause an insect's growth rate to increase slightly. If, after the disturbance is removed, the system returns to its original equilibrium, then the equilibrium point is said to be locally stable and is called an "attractor." Otherwise, it is said to be unstable and is a "repeller." Locally stable equilibrium points are called sinks and locally unstable ones are called saddle points or sources.
A2.1.10 Parameter
A parameter is a quantity, e.g., fecundity rate or predation rate, that is used in describing the dynamics of a state variable. Although a state variable evolves with time, a parameter is kept constant as time progresses. In this paper, parameter values are varied across ranges of values to see how they affect the qualitative behavior of the state variables. For example, increasing the fecundity rate of a population that is at equilibrium may cause the population to start oscillating.
A2.1.11 Period-doubling bifurcation
A period-doubling bifurcation occurs when a limit cycle or periodic orbit undergoes a bifurcation and there is an exchange of stability to orbits having double the period. See Seydel (1988) for a detailed explanation.
A2.1.12 Periodic orbit
The terminology periodic orbit is used to describe a state variable (e.g., population density) that is oscillating in a regular, repetitive manner. For continuous models having dimension of at least two, such an orbit is also called a limit cycle, provided that the orbit is isolated (that is, trajectories starting at points near the orbit spiral either toward or away from the cycle; Strogatz 1994).
A2.1.13 Phase portrait
Suppose our system is continuous and has two state variables, say a prey (x1) and a predator (x2). We can represent the behavior over time of both populations in a single diagram called a phase portrait. Examples are shown in Figs. 13b and
14b
. An illustration of the relationship between time plots and phase portraits can be found in Holling (1973: 3).
A2.1.14 Saddle point
A saddle point is an equilibrium point that attracts in certain directions and repels in others. Such an equilibrium point has unstable and stable manifolds. Initial points lying on these manifolds are repelled from, or attracted toward, the equilibrium point, respectively. Other initial points first may be attracted and then repelled (see Edelstein-Keshet 1988).
A2.1.15 Sink
A sink is a locally stable equilibrium point and may be either a stable node or a spiral attractor. In the case of a spiral attractor, the state variables oscillate with decreasing amplitude as they approach the equilibrium point.
A2.1.16 Soft loss of stability
This occurs at a Hopf bifurcation when there is a continuous change from stable equilibrium behavior to limit cycles of small amplitude. The amplitude of these cycles increases gradually for parameter values further from the Hopf bifurcation.
Figure 15
gives an example of soft loss of stability. See also section A2.1.5.
A2.1.17 Source
A source is an equilibrium point that is locally unstable. Any disturbance to the system will cause the state variables to move away from this point. In the case of a spiral repeller, this repulsion may be oscillatory.
A2.1.18 State variable
Suppose we are interested in a system consisting of plants, herbivores, and predators. Then the"state" of the system can be described by the relative biomasses or densities of these populations. The variables that are used in a mathematical model of the system to represent these biomasses or densities are called state variables.
A2.1.19 Transcritical bifurcation
At a transcritical bifurcation point, two equilibrium points coincide and exchange stabilities. An example is shown in Fig. 14. There are two equilibrium points, A and B, at each value of the parameter
µ.
A is stable for
µ <
µ*
and a saddle point for
µ >
µ*.
The situation is reversed for B. Figures 14b(i) and (ii) show possible phase portraits in two dimensions for
µ =
µ1
and
µ =
µ2.
Note that the bifurcation diagram in Fig. 14a only indicates the positions of the equilibrium points in terms of one of the state variables, x1.
A2.2 Introduction to dynamical systems concepts
In this paper, I am more interested in obtaining qualitative than quantitative information about model behavior. That is, I am more interested in finding out how varying a parameter value affects the modes of behavior of a model, rather than finding the exact parameter values at which these changes occur. Berlinski (1976) notes that qualitative insights are at a much greater depth than partially quantitative results. Because of the uncertainty associated with parameter values in nature (Hadamard 1952, Frank 1978, Swart 1987), and because models are necessarily simplifications of reality, the exact quantitative predictions of a model have little significance. It is the type or mode of behavior that is most important.
Qualitative analyses are concerned mainly with long-term rather than transient behavior. Transient dynamics vary with the initial values of variables and the time period over which solutions are calculated, whereas qualitative studies deal with the eventual behavior of the system once the initial transients have died away.
There are many different modes of behavior that characterize the long-term dynamics of a model. Suppose that the modelØs state variables represent interacting populations. In the long term, any given population may become extinct, reach a stable equilibrium, or oscillate in time. Another mathematical possibility is that a population may grow indefinitely, although this is not biologically plausible except for short time periods. As one or more parameters are varied, it is possible to change from one mode of behavior to another.
Consider the following two-dimensional model due to Bazykin (1974):
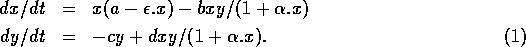
Here, x represents prey density and y predator density. The term ax describes the exponential growth of the prey population in the absence of predators, and
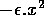 takes into account intraspecific competition among prey. In the absence of the predator, the prey population experiences logistic growth. The term - cy describes the exponential decline in the predator population in the absence of prey. The Holling type-II functions (Holling 1965)
takes into account intraspecific competition among prey. In the absence of the predator, the prey population experiences logistic growth. The term - cy describes the exponential decline in the predator population in the absence of prey. The Holling type-II functions (Holling 1965)
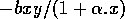 and
and
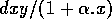 describe the interaction between the two populations.
describe the interaction between the two populations.
If intraspecific competition in the prey population is sufficiently intense (i.e.,
 is sufficiently large), then the prey population reaches a stable equilibrium. However, the equilibrium value is too low to support the predator population and this forces the predator into extinction.
is sufficiently large), then the prey population reaches a stable equilibrium. However, the equilibrium value is too low to support the predator population and this forces the predator into extinction.
If
 is decreased, thus reducing competition among prey, then the predator-prey interaction becomes relatively more important and both populations reach stable equilibria.
is decreased, thus reducing competition among prey, then the predator-prey interaction becomes relatively more important and both populations reach stable equilibria.
If
 is decreased further, the dynamics become more complicated. Instead of reaching a stable equilibrium, the two populations oscillate in time in a sustained manner. This is known as stable limit cycle behavior. For any positive initial values, the predator and prey populations oscillate, with the amplitudes of the oscillations increasing or decreasing until the regular oscillatory pattern corresponding to the limit cycle is reached.
is decreased further, the dynamics become more complicated. Instead of reaching a stable equilibrium, the two populations oscillate in time in a sustained manner. This is known as stable limit cycle behavior. For any positive initial values, the predator and prey populations oscillate, with the amplitudes of the oscillations increasing or decreasing until the regular oscillatory pattern corresponding to the limit cycle is reached.
The exact values of
 at which the previously mentioned changes in qualitative behavior occur are known as bifurcation points. In particular, the transition between equilibrium behavior and limit cycle behavior is known as a Hopf bifurcation (at least in this case; limit cycles can also be generated in other ways).
at which the previously mentioned changes in qualitative behavior occur are known as bifurcation points. In particular, the transition between equilibrium behavior and limit cycle behavior is known as a Hopf bifurcation (at least in this case; limit cycles can also be generated in other ways).
Figure 15
is an example of a one-parameter bifurcation diagram. These diagrams summarize the phase portraits corresponding to different (fixed) values of a parameter, showing how the qualitative behavior of a system of equations changes as a parameter is varied across a range of values. The parameter in question is plotted on the x -axis and one of the state variables (in this case, x) is plotted on the y -axis. Solid lines represent stable equilibria, dotted lines represent unstable equilibria, and solid circles indicate the maxima and minima of stable limit cycles. In order to interpret a bifurcation diagram, imagine the phase portraits corresponding to different values of the parameter. This is done by choosing a particular value of the parameter and mentally drawing a vertical line at that value. The points at which this line crosses the curves in the bifurcation diagram will indicate the points (in terms of the quantity on the y -axis) at which equilibria or limit cycles occur, as well as the stability of these phenomena. This information can be used to construct a possible phase portrait.
From Fig. 15, we can see that for
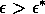 x reaches a stable equilibrium from any initial value, as indicated by the arrows. But for
x reaches a stable equilibrium from any initial value, as indicated by the arrows. But for
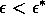 the equilibrium is unstable and the system is attracted instead toward
the stable limit cycle. The maxima and minima of the limit cycle (with
respect to x) are indicated by the solid circles. Notice that the amplitude of the limit cycle oscillations increases as
the equilibrium is unstable and the system is attracted instead toward
the stable limit cycle. The maxima and minima of the limit cycle (with
respect to x) are indicated by the solid circles. Notice that the amplitude of the limit cycle oscillations increases as
 decreases.
decreases.
Whereas phase portraits and time plots represent the dynamics of the system for a fixed set of parameter values, bifurcation diagrams summarize the dynamics for a whole range of parameter values. They show where stable equilibria or limit cycles can be expected, and can also indicate whether multiple stable states are possible at a given parameter value, or whether extinction can be expected. Thus, bifurcation diagrams provide more concise and complete information than other graphical methods (Collings et al. 1990). Each parameter can be varied in turn to see what effect it has on the dynamics. Hence, instead of using trial and error to locate the parameter combinations giving rise to oscillations or other behavior, we now have a more systematic method.
A drawback of the dynamical systems approach is that the mathematics required to obtain a bifurcation diagram can be quite formidable, especially when large models are involved. Fortunately, in recent years, many computer packages have become available to simplify the task. I used XPPAUT (Ermentrout 1994) and DSTOOL (Back et al. 1992) to obtain the results in this paper. XPPAUT has a graphical interface for the continuation and bifurcation package AUTO86 (Doedel 1981). I shall refer to AUTO rather than XPPAUT when making use of this interface. In
Appendix 3, I demonstrate how these packages can be used and illustrate the reliability of AUTO's routines by reproducing and, in fact, improving upon the results that Bazykin obtained by hand for his model (Eq. A2.1).
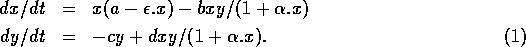
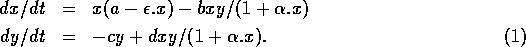
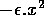 takes into account intraspecific competition among prey. In the absence of the predator, the prey population experiences logistic growth. The term - cy describes the exponential decline in the predator population in the absence of prey. The Holling type-II functions (Holling 1965)
takes into account intraspecific competition among prey. In the absence of the predator, the prey population experiences logistic growth. The term - cy describes the exponential decline in the predator population in the absence of prey. The Holling type-II functions (Holling 1965)
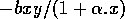 and
and
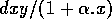 describe the interaction between the two populations.
describe the interaction between the two populations.
 is sufficiently large), then the prey population reaches a stable equilibrium. However, the equilibrium value is too low to support the predator population and this forces the predator into extinction.
is sufficiently large), then the prey population reaches a stable equilibrium. However, the equilibrium value is too low to support the predator population and this forces the predator into extinction.
 is decreased, thus reducing competition among prey, then the predator-prey interaction becomes relatively more important and both populations reach stable equilibria.
is decreased, thus reducing competition among prey, then the predator-prey interaction becomes relatively more important and both populations reach stable equilibria.
 is decreased further, the dynamics become more complicated. Instead of reaching a stable equilibrium, the two populations oscillate in time in a sustained manner. This is known as stable limit cycle behavior. For any positive initial values, the predator and prey populations oscillate, with the amplitudes of the oscillations increasing or decreasing until the regular oscillatory pattern corresponding to the limit cycle is reached.
is decreased further, the dynamics become more complicated. Instead of reaching a stable equilibrium, the two populations oscillate in time in a sustained manner. This is known as stable limit cycle behavior. For any positive initial values, the predator and prey populations oscillate, with the amplitudes of the oscillations increasing or decreasing until the regular oscillatory pattern corresponding to the limit cycle is reached.
 at which the previously mentioned changes in qualitative behavior occur are known as bifurcation points. In particular, the transition between equilibrium behavior and limit cycle behavior is known as a Hopf bifurcation (at least in this case; limit cycles can also be generated in other ways).
at which the previously mentioned changes in qualitative behavior occur are known as bifurcation points. In particular, the transition between equilibrium behavior and limit cycle behavior is known as a Hopf bifurcation (at least in this case; limit cycles can also be generated in other ways).
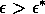 x reaches a stable equilibrium from any initial value, as indicated by the arrows. But for
x reaches a stable equilibrium from any initial value, as indicated by the arrows. But for
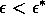 the equilibrium is unstable and the system is attracted instead toward
the stable limit cycle. The maxima and minima of the limit cycle (with
respect to x) are indicated by the solid circles. Notice that the amplitude of the limit cycle oscillations increases as
the equilibrium is unstable and the system is attracted instead toward
the stable limit cycle. The maxima and minima of the limit cycle (with
respect to x) are indicated by the solid circles. Notice that the amplitude of the limit cycle oscillations increases as
 decreases.
decreases.