|
|
|
Copyright © 2004 by the author(s). Published here under license by The Resilience Alliance.
The following is the established format for referencing this article:
Lusseau, D. 2004. The energetic cost of path sinuosity related to road density in the wolf community of Jasper National Park. Ecology and Society 9(2): r1. [online] URL: http://www.ecologyandsociety.org/vol9/iss2/resp1/
Response to Whittington et al. 2004. "Path tortuosity and the permeability of roads and trails to wolf movement" The Energetic Cost of Path Sinuosity Related to Road Density in the Wolf Community of Jasper National Park David Lusseau
University of Aberdeen
- Introduction
- Added Cost of Transport
- Energetic Cost
- Conclusions
- Responses to this Article
- Literature Cited
Published: September 2, 2004
In their recent article, Whittington et al. (2004) show that wolf packs increase their path sinuosity in the vicinity of roads and highly used trails. This path variable is defined as the relationship between the length of the path traveled (L) and the net displacement of the animal (R). The authors present a model that explains path sinuosity using the distance to prey and the density of roads and trails. Such studies demonstrate the potential impact of human developments on wild animals. However, wildlife management often requires assessing whether a proposed human activity presents a significant risk for a species. Assessing long-term risks is difficult in studies that occur over brief ecological time scales. The type of response variables collected by Whittington et al. (2004) can help to relate the short-term effects of anthropogenic activities to their long-term consequences. Path sinuosity can be related to an individual's cost of transport, i.e., the amount of energy the individual needs to travel a given distance. This in turn can be related to road and trail density thanks to Whittington et al.'s model. This forecasting model can then be used to assess the added cost of transport (in kcal • kg-1 • km-1) for each individual wolf in terms of roads and trails. This value can then be extrapolated for the two packs (13 individuals), and the added energetic cost to the ecosystem, i.e., the amount of energy wolves need to consume to meet the added cost of transport, can be balanced with the known amount of energy, i.e., prey, available. This approach greatly simplifies reality, but it can help approximate the cost of road and trail construction at a population level.
Using the linear mixed-effects model for path sinuosity described in Whittington et al. (2004), I calculated the net displacement of wolves travelling 5 km in a location where there were no roads or trails. I then varied trail, road, and prey variables to imitate varying degrees of road impact (trail and road density = 0, 0.5, 5, and 10 km/km 2) and distance to prey (0.5, 5, and 13 km). Finally, I calculated what path length wolves would need to travel to cover the same net distance as in the no-impact situation, given the path sinuosity obtained from the model for various values of road and trail densities. This shows that, for high road and trail densities (10 km/km2), wolves need to double the distance traveled to obtain the same net displacement. The cost of travel is therefore increased substantially in these situations. The availability of prey interacts with these costs; wolves travel in a straighter line as prey is being tracked (Whittington et al. 2004:Fig. 4). Distance to prey therefore decreases the added distance traveled from 32 to 29 km for distances to prey varying from 0.5 to 13 km at high road and trail densities (10km/km2).
Using scaling laws for the cost of transport in quadrupeds, it is possible to derive an approximation of the amount of energy a wolf would need to meet these extra costs. According to Tucker (1975), the cost of transport, C (in kcal • kg-1 • km-1) for a running quadruped is related to the mass, M (in kg), of the animal:
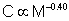 | (1) |
The road and trail impact, calculated as the difference in path length with the no-impact situation for the same net displacement, can then be related to the energetic cost for a typical male, female, and juvenile wolf. Males typically weigh 44 kg, females 37 kg, and juveniles 25 kg (Murray and Lariviére 2002). Their costs of transport are therefore approximately 0.88, 0.95, and 1.1 kcal • kg-1 • km-1 respectively (Tucker 1975). For an animal traveling 30 km/day (Whittington et al. 2004), the total daily added cost of traveling in an area with 10km/km2 of roads and trails and with prey in close proximity, i.e., 500 m, is 1265 kcal for males, 1148 kcal for females, and 898 kcal for juveniles.
Finally, once the size composition of the wolf pack is known, the total energetic demand for the wolf community can be derived (Fig. 1). Assuming that Pack 1 is composed of four females, four males, and two juveniles and that Pack 2 consists of one male, one female, and one juvenile, the total daily added cost of transport for high road and trail densities (10 km/km2) and short distance to prey (0.5 km) is approximately 14,765 kcal. Therefore, the presence of roads and trails decreases the carrying capacity of an area. These added energetic demands can be met by increasing predation in the area. However, road and trail density tends to also affect the presence of prey (Vistnes and Nellemann 2001). Therefore, it is unlikely that the packs will meet substantial added energetic demands by increasing predation. They would have to increase or shift their home range, which can lead to increased intra- and interspecific competition. In addition, this impact may result in social disruption within and between packs because males and females have to meet different costs (Conradt and Roper 2000).
Estimating the energetic cost roughly for individual wolves and packs allows the biological significance of road and trail development to be assessed before they are put in place. In addition, this technique can quantify an energetic cost in calories for various impacts on various species. It therefore allows for interspecific comparisons of the costs of anthropogenic activities and can help manage locations in which various predator species interact.
However, the approach described above would benefit from being refined for several reasons. The main issue is that the path tortuosity model explains only a small proportion of the data's variance (Whittington et al. 2004), and therefore other unmeasured parameters play an important role in defining wolf movement. Furthermore, my estimates of energetic cost are imprecise for two reasons, which could be addressed. First, I estimated the coefficients using the figure provided in the article because the equation of the linear mixed-effect model was not given. Using the equation itself would produce more accurate results. Second, I used only crude measurements for the weight of animals, and the cost of transport will vary seasonally. However, with refinement, this framework could be extended to other studies that track animal movement to allow the energetic cost of anthropogenic activities on various species to be assessed.
Responses to this article are invited. If accepted for publication, your response will be hyperlinked to the article. To submit a comment, follow this link. To read comments already accepted, follow this link.
Conradt, L., and T. J. Roper. 2000. Activity synchrony and social cohesion: a fission-fusion model. Proceedings of the Royal Society of London, Series B 267:2213-2218.
Murray, D. L., and S. Lariviére. 2002. The relationship between foot size of wild canids and regional snow conditions: evidence for selection against a high footload. Journal of Zoology 256:289-299.
Tucker, V. A. 1975. The energetic cost of moving about. American Scientist 63:413-419.
Vistnes, I., and C. Nellemann. 2001. Avoidance of cabins, roads, and power lines by reindeer during calving. Journal of Wildlife Management 65:915-925.
Whittington, J., C. C. St. Clair, and G. Mercer. 2004. Path tortuosity and the permeability of roads and trails to wolf movement. Ecology and Society 9(1): 4 [online] URL: http://www.ecologyandsociety.org/vol9/iss1/art4.
Address of Correspondent:
David Lusseau
University of Aberdeen
School of Biological Sciences
Lighthouse Field Station
George St., Cromarty,
Ross-shire IV11 8YJ, Scotland
Phone: (44) 1381 600 548
Fax: (44) 1381 600 548
d.lusseau@abdn.ac.uk