|
|
|
Copyright © 2002 by the author(s). Published here under license by The Resilience Alliance.
Go to the pdf version of this article.
The following is the established format for referencing this article:
Carlson, M. and F. Schmiegelow. 2002. Cost-effective sampling design applied to large-scale monitoring of boreal birds. Conservation Ecology 6(2): 11. [online] URL: http://www.consecol.org/vol6/iss2/art11/
Report Cost-effective Sampling Design Applied to Large-scale Monitoring of Boreal Birds Matthew Carlson and Fiona Schmiegelow
University of Alberta
- Abstract
- Introduction
- Methods
- Results
- Discussion
- Responses to this Article
- Acknowledgments
- Literature Cited
Despite their important roles in biodiversity conservation, large-scale ecological monitoring programs are scarce, in large part due to the difficulty of achieving an effective design under fiscal constraints. Using long-term avian monitoring in the boreal forest of Alberta, Canada as an example, we present a methodology that uses power analysis, statistical modeling, and partial derivatives to identify cost-effective sampling strategies for ecological monitoring programs. Empirical parameter estimates were used in simulations that estimated the power of sampling designs to detect trend in a variety of species’ populations and community metrics. The ability to detect trend with increased sample effort depended on the monitoring target’s variability and how effort was allocated to sampling parameters. Power estimates were used to develop nonlinear models of the relationship between sample effort and power. A cost model was also developed, and partial derivatives of the power and cost models were evaluated to identify two cost-effective avian sampling strategies. For decreasing sample error, sampling multiple plots at a site is preferable to multiple within-year visits to the site, and many sites should be sampled relatively infrequently rather than sampling few sites frequently, although the importance of frequent sampling increases for variable targets. We end by stressing the need for long-term, spatially extensive data for additional taxa, and by introducing optimal design as an alternative to power analysis for the evaluation of ecological monitoring program designs.
KEY WORDS: allocation of sample effort, boreal birds, community metrics, cost-effective sample design, forest bird populations, long-term monitoring, partial derivatives, power analysis, sample error, temporal and spatial variation, trend detection.
Published: November 25, 2002
Ten years have passed since ratification of the Convention on Biological Diversity, a landmark, international conservation commitment. However, the conservation of biodiversity continues to be constrained by our inability to reliably predict the effects of environmental perturbations on biota (Walters and Holling 1990). Given this uncertainty, an information feedback loop is required to assess the impact of human activities on biodiversity. Ecological monitoring, the repeated measurement of biotic response to disturbance (Hinds 1984), provides this feedback, thereby facilitating adaptive management (Halbert 1993) and the establishment of conservation and research priorities (Burbidge 1991, Stork and Samways 1995). Large-scale monitoring, where detection of long-term trends over broad spatial scales is the goal, improves our ability to distinguish human impacts from natural changes (Spellerberg 1991) and allows inference at scales relevant to policy (Urquhart et al. 1998).
Although large-scale ecological monitoring is required to conserve biodiversity (Johnson 1993, Minister of Supply and Services 1995), examples of such programs remain rare, in large part due to the difficulty of achieving effective monitoring data under cost constraints (Committee on Environment and Natural Resources 1997). The magnitude of this challenge is illustrated by the Environmental Monitoring and Assessment Program (EMAP), designed to monitor the status and trends of ecological resources in the United States (U.S. Environmental Protection Agency 2000). Although the program had a large investment of effort and money, a review deemed it unlikely to succeed, due in part to insufficient sampling intensity (National Research Council 1995).
Sampling design is critical to the effectiveness of a monitoring program (Dixon et al. 1998) because it determines the quality of the resulting parameter estimates (Thompson et al. 1998). In many instances, the parameter of interest is a long-term trend in population size or community structure. The ability of a design to provide reliable trend estimates can be interpreted as the probability that it will detect a trend, should one exist. Statistical power is a suitable measure to gauge the influence of sample effort on data quality (e.g., Peterman 1990, Gibbs et al. 1998). A low-power monitoring program will have little chance of detecting all but catastrophic trends, thereby providing an illusion of stability and preventing remedial action required to conserve biodiversity (Fairweather 1991).
The power to detect a trend of specified magnitude, with a given level of significance, is negatively related to variability and positively related to sample effort. Although increasing sample effort increases power to detect trend, excessive sampling wastes limited monitoring resources (Bernstein and Zalinski 1983). Extensive monitoring requirements that must be met under budgetary constraints have made cost-effective monitoring a research priority (Committee on Environment and Natural Resources 1996, Schneider et al. 1999). Funding limitations impose trade-offs between the allocations of effort to sample effort components, which compete for monitoring resources (Millard and Lettenmaier 1986). It follows that cost-effective monitoring design requires an understanding of the efficiency of allocating effort to sample effort components.
Here we investigate cost-effective sampling strategies for large-scale avian monitoring. As a group, birds are suited to monitoring beause there are well-established (Bibby et al. 1992) and efficient (e.g., Croonquist and Brooks 1991) sampling protocols that achieve informative data due to the diverse responses of bird species to disturbance (Steele et al. 1984). We evaluate monitoring strategies in the context of the forested region of Alberta, Canada, where development of a large-scale forest biodiversity monitoring program is underway (Farr et al. 1999).
The design of a large-scale avian monitoring program can be generalized as follows (Fig. 1). Sampling occurs at multiple sites located randomly or systematically within the region of interest. Sampling spans multiple years, although monitoring may not occur every year. Within a sample year, sites are surveyed one or more times. At each site, birds are counted using one or more point-count stations, the preferred counting method for large-scale monitoring in forested regions (Verner 1988). We focus on the power and cost trade-offs implicit in allocating effort to the number of sites, the frequency with which these sites are sampled, and the number of stations and surveys used to sample the sites.
To identify cost-effective sampling strategies, power and cost analyses were integrated. The power of sampling designs to detect trends in a selection of bird species and community metrics was estimated by simulating monitoring data, using mean and variance parameters estimated from empirical data. Based on the power estimates, a functional relationship between sample effort and power was derived for each monitoring target. A functional relationship between sample effort and cost was also identified. Partial derivatives of the functional relationships were taken to estimate rates of power and cost gain with sample effort. Comparison of these rates across sample effort parameters identified cost-effective sampling strategies.
Estimation of avian mean and variance parametersStochastic variability enters data collected via three components, according to Fig. 1. Data fluctuate at a site across years because of temporal variability in abundance and sample (methodological) error, which are captured by the within-site temporal variance (τ12) component. Sample error, which includes both variation in the proportion of birds present that are detectable, e.g., singing (due to factors such as weather) and variation in the proportion of birds that are detected due to observer ability, is expected to decrease with increased sample effort. This effect was evaluated by estimating τ12 at multiple levels of within-site effort. In addition to temporal variability, data fluctuate spatially in two ways. The distribution of individuals across sites at the start of the monitoring period is not uniform, and is accounted for by between-site initial variance (τ22). Trend magnitude also varies across sites about the regional trend mean, and is accounted for by between-site trend variance (τ32). Because sample error is included in τ12, it was extracted from spatial variance estimates to the extent possible, to avoid double counting. Simulation of data therefore required estimation of τ12, τ22, τ32, as well as mean initial abundance (θ0). Because we were interested in evaluating monitoring program design for the boreal forest of Alberta, data collected from this region were used for parameter estimation. τ12 and θ0 were estimated using data collected at three 100-ha control sites near Calling Lake, in north-central Alberta, over a 6-year period (1993–1998). The sites, part of a long-term experimental fragmentation study (Schmiegelow et al. 1997), occur in boreal mixed-wood forest, an ecotype representative of much of northern Alberta. At each site, 20 stations were sampled four times each year (surveys) during the breeding season (from late May to late June), at 10-d intervals, using 5-min point counts. Control sites (old forest devoid of forestry activity) were used to minimize the effect of non-natural (treatment) variation, which can exaggerate within-site temporal variation (Gibbs et al. 1998). τ22 and τ32 were estimated using Breeding Bird Survey (BBS) data (USGS Patuxent Wildlife Research Center 2000) collected from the closed boreal forest physiographic region of Alberta. The BBS is a volunteer-based long-term monitoring program spanning Canada and the United States. The program consists of routes that are sampled by volunteers each year during the breeding season (May or June). At each route, birds are sampled at 50 point count stations, each 3 min in duration, along 24.5-mile [39.4 km] routes (see Droege [1990] for additional BBS design information). All variance parameters were estimated as coefficients of variation (standard deviation divided by the mean) to make the estimates suitable for use in simulation studies. Details on parameter estimation are available in Appendix 1.
Species and community metric selectionTo include species covering the spectrum of variance characteristics, we selected them using a plot of τ12 and τ22 estimates. As broad community measures, total species richness, species richness of the ground-nesting guild (see Appendix 1), and the Shannon-Weiner diversity index (Margalef 1958) were also included.
Power simulationsPower of 160 sampling designs (Table 1) was estimated for each species and community metric, using mean abundance and variance estimates in a Monte Carlo simulation approach (Appendix 2), following the methodology of Gibbs et al. (1998). Simulated trends were exponential and 20 years in length, with magnitudes of –3% and –1% per year for populations and community metrics, respectively.
Modeling the effect of sample effort on power and cost
Multiple regression was applied to develop models for each target that expressed power as a function of sample effort. A linear model was unsuitable due to the asymptotic nature of power as it approaches the 100% maximum. Instead, power estimates were fit to the following nonlinear model:
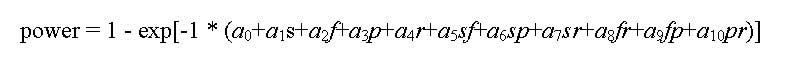 |
[1] |
where a0-10 are model coefficients and s, f, p, and r are number of sites, sample frequency, point-count stations, and surveys, respectively. The model was fit to the power estimates by minimizing the residual sum of squares using procedure NLS in S-Plus (MathSoft 1999). Residual analysis indicated no violations of normality and homogeneity assumptions. A model relating sample effort to program cost is presented in Appendix 3.
Determining efficient sampling strategiesTo evaluate the efficiency of allocating sample effort to each effort parameter, we estimated partial derivatives of the power and cost models for each effort parameter. Partial derivatives were interpreted as the increase in power or cost achieved by increasing the number of sites, sample frequency, point-count stations, or surveys by one, within the range of effort levels simulated (Table 1). Average effort levels of designs achieving between 80% and 90% power for each species/community metric were used to solve partial derivatives, in order to evaluate the efficiency of sampling strategies in close proximity to the 90% power goal. The significance of power partial derivatives, which were estimated from regression models, was tested using z tests. The standard errors of partial derivatives were estimated using the Krinsky-Robb method (Krinsky and Robb 1986). This required generation of 10,000 coefficient vectors by drawing random vectors from a multivariate normal distribution with mean and variance as estimated from nonlinear regression. Using the generated coefficient vectors, we calculated 10000 partial derivatives to approximate the distribution of the partial derivative, from which standard error was calculated. Normally distributed residuals from the regressions validated the required assumption of multivariate normality (Myers 1990).
Because power and cost were expressed in different units, it was necessary to convert partial derivatives to proportions for comparison. For example, partial derivatives of power related to each effort parameter were divided by the sum of power partial derivatives across effort parameters. We calculated 95% confidence intervals of power proportions by estimating 10,000 power proportions using the approximated power partial derivative distributions, and eliminating the top and bottom 2.5% of the distributions. For a given effort parameter, if the power proportion was greater than the cost proportion, the rate at which power increased by allocating effort to that parameter, relative to the other parameters, was greater than the rate at which cost increased, indicating efficiency. If, on the other hand, the cost proportion was greater, the cost of allocating effort to that parameter, relative to the other parameters, was greater than the power gains achieved, indicating inefficiency.
In addition to the three community metrics, eight species were selected for the analysis (Fig. 2), two from each of the following categories: ubiquitous (low spatial and temporal variance), temporally fluctuating (low spatial and high temporal variance), spatially patchy (high spatial and low temporal variance), and irruptive (high spatial and temporal variance). Averaged across selected species and community metrics, τ22 was greatest in magnitude (1.143 for species and 0.203 for community metrics), followed by τ12 (1.083 and 0.0787) and τ32 (0.303 and 0.0507). Full presentation of parameter estimates, including the influence of within-site effort on τ12, is provided in Tables 2–5. Relationships between variability and species abundance were explored by ranking the order of abundance and calculating a correlation coefficient for each variance parameter. There was a strong negative relationship between abundance and τ12 (r = -0.976; P = 0.000). Abundance rank was also negatively correlated with the other two parameters, although the relationships were weaker (r = -0.714; P = 0.047 for τ22 and r = -0.476; P = 0.233 for τ32).
In general, power increased with each sample effort parameter (Figs. 3–6). Power was highly sensitive to τ12, moderately sensitive to τ22, and only minimally sensitive to τ 32 (Table 6). Eq. 1 effectively modeled the relationship between power and sample effort, explaining much of the variability in power estimates (R2 = 0.94 – 0.98). Models were not generated for species or community metrics for which all sampling designs achieved > 90% power. This excluded the Shannon-Weiner diversity index, species richness, and the White-throated Sparrow (Zonotrichia albicollis). Power to detect trend increased as the cost of monitoring programs increased, although the relationship was highly nonlinear (Fig. 7). Power partial derivatives were generally positive and significant (Table 7), as were cost partial derivatives except for point-count stations, reflecting the assumption that increasing the number of stations across the range simulated (4–16) incurred no additional cost (Appendix 3). This assumption, combined with positive rates of increase in power with point-count stations, implied efficiency. Thus point-count stations were excluded from further analysis. Table 8 presents results of the efficiency analysis, evaluated with reference to sampling designs achieving between 80% and 90% power. To evaluate the sensitivity of efficiencies to power level, the analysis was repeated using average effort levels from designs achieving: <60%, 60–70%, 70–80%, and >90% power. Efficiencies were consistent across power intervals, with the exception of the efficiency of surveys for the Yellow Warbler (Dendroica petechia) and for species richness of the ground-nesting guild. Although surveys were marginally efficient for these targets when designs achieved > 80% power, they were marginally inefficient when designs achieved < 80% power.
Recent political support for biodiversity monitoring is providing new opportunities to obtain spatially and temporally extensive data sets. Maximizing these opportunities to achieve exciting new analyses requires efficient use of available funding. We identified cost-effective sampling strategies for forest birds, using existing data, power analysis, and statistical modeling.
Variability of bird species and community metricsBecause of the sensitivity of power to variability, and the wide range in variability across species, variance estimates were used to categorize and select targets for our analysis. Our four variance categories reflect species life-history traits. Species in the ubiquitous category have broad niches that buffer them from both temporal and spatial environmental variation. In comparison, spatially patchy species have narrow niches that allow occupancy of only a subset of available habitat, although occupancy is consistent across years. Species in the temporally fluctuating and irruptive categories may be tied to temporally fluctuating habitat characteristics, such as food availability. Other species may appear to be temporally variable due to sampling issues. For example, the Pileated Woodpecker (Dryocopus pileatus) is not an irruptive species, but its large home range relative to the scale of point-count stations resulted in variable counts, even in the presence of a potentially stable population.
Ubiquitous species will be easiest to monitor, due to the negative relationship between species abundance and the variance parameters. Their broad habitat requirements, however, imply less sensitivity to disturbance, reducing their value for monitoring. Rare species, although of greater monitoring interest, will require increased sampling intensity to mitigate high sample error (Link et al. 1994), as well as high natural variability, perhaps caused by specialized habitat requirements. If the expense associated with monitoring such species is prohibitive, careful selection of target species that are sensitive to disturbance, yet exhibit low variability, is recommended. Temporal variation tends to influence power to a greater extent than does spatial variation. Species in the spatially variable category (i.e., the Black-throated Green Warbler, Dendroica virens), may be examples of efficient targets because of their habitat specificity and relative temporal stability.
Monitoring of community metrics provides an alternative. In this study, all community metrics exhibited less variance than even the most common species, which translated into low sample effort requirements. However, two issues must be resolved. First, the sensitivity of community metrics to disturbance must be determined. We used a smaller magnitude change in community metric power analyses to account for a presumed reduction in sensitivity to disturbance, relative to populations of species. The magnitude of the reduction was subjective, however, and may not have adequately accounted for the relative stability of community metrics. Second, it is not clear which community metric, or combination of metrics, provides meaningful information on the status of the bird community, and interpretation of community metrics is difficult. Nevertheless, the relative low cost of monitoring community metrics is promising and warrants increased research into their use.
Power estimates, and therefore our conclusions regarding cost-effective sampling strategies, were contingent on assumptions made when estimating variance parameters. A discussion of these assumptions is presented at the end of Appendix 1.
Cost-effective sampling strategiesAlthough all effort parameters generally had a positive and significant influence on power, the magnitude of their influence and costs differed. Therefore, to establish efficient sampling design strategies, we compared rates of increase in power to rates of increase in cost across effort parameters. To focus on the response of power and cost to sample effort near the 90% power goal, we used average effort levels across designs achieving between 80% and 90% power. Efficiencies were consistent across power levels, however, indicating that the cost-effective sampling strategies reported here are not restricted to designs achieving between 80% and 90% power. Because optimal effort allocation depends on the relative magnitude of variance parameters (Bernstein and Zalinski 1983), one would expect sampling efficiencies to vary across monitoring targets that exhibit different variance characteristics. The inclusion of multiple species and community metrics allowed comparison of sampling efficiencies across different targets, which identified consistent sampling efficiencies across targets, and efficiencies contingent on the variance characteristics of the monitoring target.
When designing a monitoring program, one must decide whether to monitor more sites infrequently, or fewer sites frequently. Allocation of effort to the number of sites was efficient for all monitoring targets, suggesting that increasing site density is a component of an efficient avian monitoring design (see also Link et al. 1994). Previous evaluation of the power of long-term avian sampling designs has assumed that sampling occurs every year (e.g., Gibbs and Melvin 1997, Gibbs et al. 1998, Lewis and Gould 2000). However, high sampling frequency is costly. We used simulations to estimate power for a range of sampling frequencies to evaluate the efficiency of allocating effort to sampling frequency. In general, the rate at which power increased with sample frequency was greater for temporally variable species. For temporally stable monitoring targets, however, the increase in data quality achieved by increasing sampling frequency was small, and thus inefficient. These results suggest that more sites should be sampled relatively infrequently, although higher sampling frequency will be required for temporally variable targets. The number of sites rises in importance when sampling uncommon species, if sites with zero counts over the study period are eliminated from the analysis, as is the case with the BBS (Thomas 1997). This effectively reduces the sample size, so that the number of sites must be increased to account for the proportion expected to have zero counts. Similarly, more frequent monitoring will be necessary if detection of cyclical or irregular trends is required, rather than the constant trends simulated here (Scott 1998). If counts are expected to vary coherently across sites about a temporal trend (i.e., if they exhibit cyclic tendency), panel designs are an efficient strategy whereby some sites are sampled more frequently than others (Urquhart et al. 1998).
Two strategies for reducing sample error were evaluated: increasing the number of point-count stations and increasing the number of surveys at a station within a year. Sampling the maximum number (16) of point-count stations considered was always efficient because it increased power and incurred no additional cost compared to sampling fewer point count stations. Although sampling of additional stations is not, in reality, free, the associated cost will be minimal compared to the cost of accessing sites, particularly where access is limited. In our case, one crew could visit only a single site on a given day due to logistical constraints, and could sample up to 16 point-count stations. As long as additional within-site sampling (i.e., point-count stations) reduces sample error, high within-site, within-survey sample effort should be a component of a large-scale monitoring program. Repeated surveys within a year, on the other hand, were generally inefficient. Although they are marginally efficient for some temporally stable species and metrics, multiple surveys will usually be unnecessary to detect trends in these targets. Surveys were dramatically inefficient for species requiring high sample effort to detect trends, suggesting that repeated visits to a site within a year are not cost-effective (see also Link et al. 1994). Allocating effort to achieve consistent timing of surveys across years was also inefficient, based on the negligible effect of timing on temporal variance. This result is fortunate, as consistent timing of surveys is difficult to achieve in large-scale monitoring. However, if potential sample dates were to extend beyond the one-month period during which our baseline data were collected (i.e., the peak of breeding activity for many species), the importance of survey timing should increase.
Extending the analysis to additional taxaComprehensive monitoring of biodiversity must include diverse taxa. This ambitious goal might best be achieved through a single, broad-based biodiversity monitoring program, rather than a collection of specialized programs. To facilitate design of such a program, our analysis should be extended to multiple taxa. An extensive search for data sets to facilitate parameter estimation for our study area revealed severe limitations (S. Rangen and W. Schaffer, unpublished report). In shortest supply were data collected across multiple years (necessary to estimate τ12 and τ32); in addition to birds, such data were only available for components of terrestrial vegetation and aquatic macroinvertebrates. This stresses the need for implementation of long-term monitoring programs.
Alternative sample designWe interpreted the problem of designing a cost-effective monitoring program as achieving high power to detect trend at low cost. An alternative framework is an optimal experimental design (Silvey 1980), in which sample design is viewed as a constrained optimization problem. The goal is to select the design that achieves maximum information under design constraints, such as cost. A model is assumed for the phenomenon of interest, and the analysis proceeds through an evaluation of the inverse of the error covariance matrix of the best linear unbiased estimator. This matrix, known as the Fisher information matrix, contains information about measurement errors and parameter sensitivities, allowing the quality of parameter estimates achieved by a design to be quantified (Versyck et al. 1999).
There is a fundamental difference in the monitoring philosophies implicit in power analysis and optimal design. Our power analysis assumed that the monitoring goal is regional detection of long-term trends using fixed sites randomly located within the region of interest. There is no consideration of site attributes, such as disturbance or habitat type. Such a program is not designed to answer a particular question, such as the effect of a disturbance type on biodiversity, but simply to detect broad-scale changes in biodiversity, regardless of the cause. This does not maximize information gain, nor can it link biodiversity trends with causal factors. Thus it restricts the translation of monitoring findings into policy change. Optimal experimental design takes a very different approach. Treatment levels at potential sites are explicitly considered in the design, in order to achieve the best estimate of the parameter of interest. Such a design has greater potential for providing estimates of the effect of specific management policies on biodiversity, thereby facilitating adaptive management. However, the long-term utility of such a monitoring program may be limited. Data from a program optimally designed to answer today’s questions are unlikely to address tomorrow’s environmental dilemmas.
The two design strategies produce different styles of monitoring programs, each with its strengths and weaknesses. Instead of relying solely on either strategy, a hybrid approach would exploit the strengths of both. This would consist of optimal designs that track the effects of specific disturbances, superimposed on a large-scale design that achieves regional trend estimates with high power.
Responses to this article are invited. If accepted for publication, your response will be hyperlinked to the article. To submit a comment, follow this link. To read comments already accepted, follow this link.
This article is the result of graduate research, and benefited greatly from the perspectives of supervisory committee members Brad Stelfox, Vic Adamowicz, and Peter Boxall. Steve Cumming provided statistical and computer programming guidance. Interaction with the Alberta Forest Biodiversity Monitoring Program Technical Committee, especially Dan Farr, was valuable. Without the hard work of those who collected the bird data, the research reported here would not have been possible. Many thanks to Breeding Bird Survey volunteers and to those who have collected data over the years at Calling Lake. Thank you also to those who provided computer code. This research was funded by the Natural Sciences and Engineering Research Council of Canada (NSERC), the Sustainable Forest Management Network, and the Alberta Forest Biodiversity Monitoring Program. The article benefited from the comments of two anonymous reviewers. Finally, thank you to family and friends for your support.
Bernstein, B. B., and J. Zalinski. 1983. An optimum sampling design and power tests for environmental biologists. Journal of Environmental Management 16:35–43.
Bibby, C. J., N. D. Burgess, and D. A. Hill. 1992. Bird census techniques. Academic Press, San Diego, California, USA.
Burbidge, A. A. 1991. Cost constraints on surveys for nature conservation. Pages 3–6 in C. R. Margules and M. P. Austin, editors. Nature conservation: cost effective biological surveys and data analysis. CSIRO, Melbourne, Australia.
Caughley, G., and A. R. E. Sinclair. 1994. Wildlife ecology and management. Blackwell Science, Cambridge, Massachusetts, USA.
Committee on Environment and Natural Resources. 1996. Integrating environmental monitoring and research in the mid-Atlantic Region. Proceedings of a Workshop, College park, maryland, 10–12 April 1996. Committee on Environment and Natural Resources, National Science and Technology Council, Washington, D.C., USA. [Available online http://www.epa.gov/cludygxb/Pubs/marrpt.pdf.]
Committee on Environment and Natural Resources. 1997. Integrating the nation’s environmental monitoring and research networks and programs: a proposed framework. Environmental Monitoring Team, Committee on Environment and Natural Resources, National Science and Technology Council, Washington, D.C., USA. [Available online http://www.epa.gov/cludygxb/Pubs/framewrk.pdf.]
Croonquist, M. J., and R. P. Brooks. 1991. Use of avian and mammalian guilds as indicators of cumulative impacts in riparian-wetland areas. Environmental Management 15:701–714.
Dixon, M., A. R. Olsen, and B. M. Kahn. 1998. Measuring trends in ecological resources. Ecological Applications 8(2):225–227.
Droege, S. 1990. The North American Breeding Bird Survey. Pages 1–4 in J. R. Sauer and S. Droege, editors. Survey designs and statistical methods for the estimation of avian population trends. Biological Report 90(1). U.S. Fish and Wildlife Service, Washington, D.C., USA.
Fairweather, P. G. 1991. Statistical power and design requirements for environmental monitoring. Australian Journal of Marine and Freshwater Research 42:555–567.
Farr, D. R., S. E. Franklin, E. E. Dixon, G. Scrimgeour, S. Kendall, P. Lee, S. Hanus, N. N. Winchester, and C. C. Shank. 1999. Monitoring forest biodiversity in Alberta: program framework. Alberta Forest Biodiversity Monitoring Program Technical Report 3. Draft Report. [Available online http://www.fmf.ab.ca/bm/reports.htm.]
Geissler, P. H., and J. R. Sauer. 1990. Topics in route-regression analysis. Pages 54–57 in J. R. Sauer and S. Droege, editors. Survey designs and statistical methods for the estimation of avian population trends. Biological Report 90(1). U.S. Fish and Wildlife Service, Washington, D.C., USA.
Gibbs, J. P., S. Droege, and P. Eagle. 1998. Monitoring populations of plants and animals. BioScience 48:935–940.
Gibbs, J. P., and S. M. Melvin. 1997. Power to detect trends in waterbird abundance with call–response surveys. Journal of Wildlife Management 61(4):1262–1267.
Halbert, C. L. 1993. How adaptive is adaptive management? Implementing adaptive management in Washington State and British Columbia. Reviews in Fisheries Science 1:261–283.
Hilborn, R., and M. Mangel. 1997. The ecological detective. Princeton University Press, Princeton, New Jersey, USA.
Hinds, W. T. 1984. Towards monitoring of long-term trends in terrestrial ecosystems. Environmental Conservation 11:11–17.
Johnson, S. P. 1993. The Earth Summit: the United Nations Conference on Environment and Development. Graham and Trotman/Martinus Nijhoff, London, UK.
Krinsky, I., and A. L. Robb. 1986. On approximating the statistical properties of elasticities. Review of Economics and Statistics 68:715–719.
Lewis, S. A., and W. R. Gould. 2000. Survey effort effects on power to detect trends in raptor migration counts. Wildlife Society Bulletin 28:317–329.
Link, W. A., R. J. Barker, J. R. Sauer, and S. Droege. 1994. Within-site variability in surveys of wildlife populations. Ecology 75(4):1097–1108.
Link, W. A., and J. S. Hatfield. 1990. Power calculations and model selection for trend analysis: a comment. Ecology 71:1217–1220.
Margalef, R. 1958. Information theory in ecology. General Systems 3:36–71.
MathSoft. 1999. S-Plus 2000. Data Analysis Products Division, MathSoft, Seattle, Washington, D.C., USA.
Millard, S. P., and D. P. Lettenmaier. 1986. Optimal design of biological sampling programs using the analysis of variance. Estuarine, Coastal and Shelf Science 22:637–656.
Minister of Supply and Services Canada. 1995. Canadian biodiversity strategy: Canada’s response to the Convention on Biological Diversity. Catalogue Number En21-134/1995E.
Myers, R. H. 1990. Classical and modern regression with applications. Duxbury Press, Belmont, California, USA.
National Research Council. 1995. Review of EPA’s Environmental Monitoring and Assessment Program: overall evaluation. National Academy Press, Washington, D.C., USA.
Peterman, R. M. 1990. Statistical power analysis can improve fisheries research and management. Canadian Journal of Fisheries and Aquatic Sciences 47:2–15.
Press, W. H., S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery. 1992. Numerical recipes in C: the art of scientific computing. Cambridge University Press, New York, New York, USA.
Schmiegelow, F. K., C. S. Machtans, and S. J. Hannon. 1997. Are boreal birds resilient to forest fragmentation? An experimental study of short-term community responses. Ecology 78:1914–1932.
Schneider, R., P. Lee, C. Shank, D. Farr, and B. Stelfox. 1999. Conceptual framework and rationale for monitoring forest biodiversity in Alberta. Pages 1–45 in D. R. Farr, S. E. Franklin, E. E. Dixon, G. Scrimgeour, S. Kendall, P. Lee, S. Hanus, N. N. Winchester, and C. C. Shank. Monitoring forest biodiversity in Alberta: program framework. Alberta Forest Biodiversity Monitoring Program Technical Report (Draft) 3. [Available online http://www.fmf.ab.ca/bm/reports.htm.]
Scott, C. T. 1998. Sampling methods for estimating change in forest resources. Ecological Applications 8(2):228–233.
Silvey, S. D. 1980. Optimal design: an introduction to the theory for parameter estimation. Chapman and Hall, London, UK.
Spellerberg, I. F. 1991. Monitoring ecological change. Cambridge University Press, Cambridge, UK.
Steele, B. B., R. L. Bayn, Jr., and C. Val Grant. 1984. Environmental monitoring using populations of birds and small mammals: analyses of sampling effort. Biological Conservation 30:157–172.
Stork, N. E., and M. J. Samways. 1995. Inventorying and monitoring: executive summary. Pages 457–458 in V. H. Heywood and R. T. Watson, editors. Global biodiversity assessment. Cambridge University Press, Cambridge, UK.
Thomas, L. 1997. Evaluation of statistical methods for estimating long-term population change from extensive Wildlife Surveys. Dissertation. University of British Columbia, Vancouver, British Columbia, Canada.
Thompson, W. L., G. C. White, and C. Gowan. 1998. Monitoring vertebrate populations. Academic Press, San Diego, California, USA.
U.S. Environmental Protection Agency. 2000. EMAP. [Available online http://www.epa.gov/emap/” Environmental Monitoring and Assessment Program Homepage.]
Urquhart, N. S., S. G. Paulsen, and D. P. Larsen. 1998. Monitoring for policy-relevant regional trends over time. Ecological Applications 8:246–257.
USGS Patuxent Wildlife Research Center. 2000. North American Breeding Bird Survey Internet data set. [Available online http://www.mp2-pwrc.usgs.gov/bbs/retrieval/disclaim.cfm.]
Verner, J. 1988. Optimizing the duration of point counts for monitoring trends in bird populations. Research Note PSW-395. Pacific Southwest Forest and Range Experiment Station, U. S. Department of Agriculture, Forest Service, Berkeley, California, USA.
Versyck, K. J., K. Bernaerts, A. H. Geeraerd, and J. F. van Impe. 1999. Introducing optimal experimental design in predictive modeling: a motivating example. International Journal of Food Microbiology 51:39–51.
Walters, C. J., and C. S. Holling. 1990. Large-scale management experiments and learning by doing. Ecology 71:2060–2068.
Address of Correspondent:
Matthew Carlson
Department of Biological Sciences
CW-405 Biological Sciences Building
University of Alberta
Alberta, Canada, T6G 2E9
Phone: (780) 492-1289
Fax: (780) 492-9234
mjc@ualberta.ca