Home | Archives | About | Login | Submissions | Notify | Contact | Search

 ES Home > Vol. 6, No. 1 > Art. 3

Copyright © 2002 by the author(s). Published here under license by The Resilience Alliance.

The following is the established format for referencing this article:
Cumming, G. S. 2002. Habitat shape, species invasions, and reserve design: insights from simple models. Conservation Ecology 6(1): 3. [online] URL: http://www.consecol.org/vol6/iss1/art3/

A version of this article in which text, figures, tables, and appendices are separate files may be found by following this link.
Report, part of Special Feature on Ralf Yorque Memorial Competition 2001

Habitat Shape, Species Invasions, and Reserve Design: Insights from Simple Models

Graeme S. Cumming

University of Florida

ABSTRACT

Species invasions have become a major threat to global biodiversity. We currently lack a general theory of species invasions that allows us to make useful predictions about when and where invasions will occur, whether they will be successful, and whether they will alter ecosystem function in invaded habitats. One line of enquiry in developing such a theory is to focus on the characteristics of successful invaders. A second, complementary approach is to examine habitats of interest more closely and ask how the properties of the habitat that is being invaded affect the likelihood of invasion success. In this paper, I consider the importance of habitat shape (also termed "habitat topology" or "habitat geometry") as a variable affecting the dispersal and abundance of invasive populations. I use two well-established simulation modeling approaches, namely, a cellular automaton model and a reaction-diffusion model, to mimic species invasions in hypothetical habitats that cover a range of linear, branching, rectangular, and square shapes. The results suggest that invasions in more geometrically complex habitats will occur faster and may ultimately produce a higher abundance of the invasive species. Differences in invasion rates are not a simple consequence of differences in overall connectivity, as shown by a comparison of habitats with identical connectivities but different spatial arrangements of cells. Ultimately, if combined with other modeling approaches, these methods may be useful in generating recommendations for managers about the vulnerability of particular habitats and reserve networks to invasion.

KEY WORDS: cellular automaton model, colonization, connectivity, dispersal, habitat complexity, habitat geometry, habitat shape, landscape ecology, reaction-diffusion model, reserve design, reserve networks, species invasion.

Published: February 13, 2002

INTRODUCTION

Human expansion of the geographical ranges of other species has become a major threat to global biological diversity. Numerous unplanned, uncontrolled experiments have shown how a wide range of invasive species including crayfish, mussels, insects, fish, birds, pathogens, and plants can affect the structure of the indigenous food web, alter key abiotic variables such as groundwater, and cause reductions in local species diversity (Parker and Reichard 1998, Parker et al. 1999). At the same time, many introductions are unsuccessful or have no effect on the structure and function of indigenous communities (Williamson and Fitter 1996). A good deal of effort has been invested in trying to understand how the intrinsic properties of invasive species such as their reproductive rates, dietary requirements, and associations with humans (Bazzaz 1986) contribute to their success or failure. Although these studies have yielded a variety of useful case studies, they have mostly failed to establish general principles to guide managers in novel instances.

Orians (1986) argues that the shift of attention away from the receiving environment to the nature of the colonizing species has contributed to the lack of progress in deriving a more general understanding of invasions. He advocates an approach that combines information about the invading organisms with information about the environments into which they are being introduced and discusses the properties of the receiving environment in terms of disturbance, biotic interactions, and temporal scale. Similarly, Parker et al. (1999) ask to what extent the impact of an invasive species is dependent on the environment into which it is introduced.

Invasions usually come as ecological surprises. Although it may not be possible to make strong predictions about the likelihood of species invasions (May 1976), we can anticipate that invasions will be more likely in some places than in others. In particular, some habitats or habitat configurations are more susceptible to invasion than others. If we can identify the general properties of habitats that make them more or less vulnerable to invasion, we need to take these properties into consideration when designing and managing conservation areas. There are many characteristics of a region that will affect the likelihood of its being successfully invaded, including:

  1. geographic isolation and proximity to potential sources of invaders (MacArthur and Wilson 1967). It should be noted that habitat proximity may be natural or anthropogenic. For example, areas on transport routes or with migratory human populations will be more vulnerable to invasion;
  2. the number of similar habitats in other parts of the world;
  3. the productivity of the habitat and the nature of the biota currently living within it (Pacala and Roughgarden 1982);
  4. the nature and frequency of relevant disturbances (Elton 1958, Hobbs and Huenneke 1992);
  5. the ease with which organisms move through the habitat as determined by relevant features such as vegetation type, wind, or water flow rates;
  6. historical factors affecting the local species pool such as recent extinctions and previous invasions (Allen et al. 1999);
  7. the specific match of invading species to habitat; and
  8. habitat size and shape.

These and other factors, such as the rate of increase and minimum viable population size of the invading species, will also determine how serious the consequences of the invasion are and the likelihood that the invading species can be controlled.

An important correlate of the risk associated with a particular introduction is the rate at which individuals of the invading species can multiply and disperse. In this paper, I examine the question of whether habitat shape can affect rates of colonization. Previous studies of habitat shape that focused primarily on metapopulations and dispersal between habitat fragments (Hamazaki 1996, Dunham et al. 1997) often ignored the relevance of habitat shape at smaller and larger scales. Although Major et al. (1999) found significantly higher robin (Erithacus rubecula) densities in larger habitat fragments and different age structures in the robin populations of large and small fragments, the scale of their analysis was such that the results must necessarily be considered in terms of between-patch rather than within-patch dispersal. As I demonstrate using two different, spatially explicit simulation methods (a cellular automaton model and a reaction-diffusion model), these processes are affected by habitat shape. The models are used to generate hypotheses about the susceptibility of different habitats to invasion. In the future, it may be possible to use this kind of approach to calibrate the relative vulnerabilities of habitat fragments and reserves to invasions.

METHODS

The spread of organisms in hypothetical habitats of different shapes was modeled using two different methods: a stochastic cellular automaton and a reaction-diffusion model. The Matlab routines for each model are provided in Appendix 1. Both methods have been widely used to study invasions (Auld and Coote 1980, Okubo 1980, Roughgarden 1986, Hengeveld 1994, Tilman and Kareiva 1997). In both instances, I kept the design of the model as simple as possible to minimize the number of parameters that might affect the outcome of the modeling exercise. All comparisons were undertaken using identical parameters and habitats of equivalent sizes (i.e., the same number of square cells) that differed only in shape.

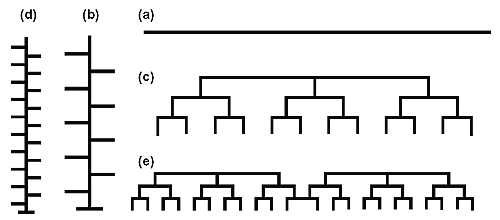
Hypothetical habitats

Each hypothetical habitat consisted of 1600 square cells (the habitat files are available in Appendix 2). Habitat shapes ranged from a straight line 1600 cells long to a 40 x 40 grid. The network habitats (Fig. 1) imitate streams of different complexities with 0, 10, and 20 nodes, respectively. Hypothetical streams of the same length and with the same number of nodes can be constructed at different levels of complexity, depending on how many ramifications their divergences have (i.e., how hierarchical they are); I constructed both a simple and a more complex model for each of the branching streams (10 and 20 nodes). Note that the complex 10-node and 20-node networks have slightly different hierarchical arrangements.

Fig. 1. Different hypothetical streamlike habitats compared in the modeling exercise (these drawings are not to scale). Each habitat consists of 1600 square cells; all parts of each network are the same width. Drawing (a) represents a linear habitat with no nodes; (b), a simple design with 10 nodes; (c), a complex design with 10 nodes; (d), a simple design with 20 nodes; and (e), a complex design with 20 nodes. Note that the complex 10-node habitat (c) has a different form from that of the complex 20-node habitat (e).

GIF Image (8 K)

The regularly shaped habitats imitate square or rectangular terrestrial areas measuring 10 x 160, 20 x 80, and 40 x 40 cells, respectively. I did not attempt to simulate the effects of increasing the number of corners, although corner cells will obviously have a lower connectivity than do perimeter cells.

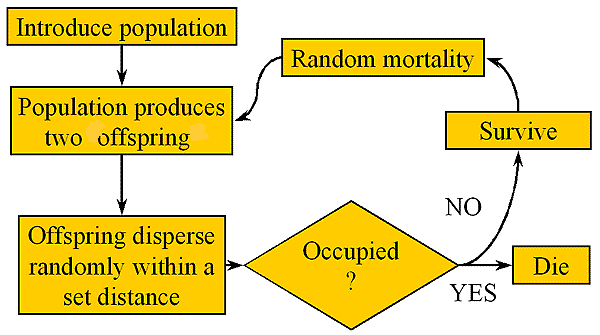
Cellular automaton model

A thorough description of cellular automata in spatial ecology can be found in Tilman and Kareiva (1997). The model follows a simple, iterative form in which, at each time step, occupied cells can produce two offspring (these "propagules" can be thought of as subpopulations or migrating individuals). The offspring are assigned randomly to any one of the cells within a user-defined maximum dispersal distance of the parent cell (Fig. 2); this distance is set at three cell widths for all simulations. If an occupied cell (value = 1) is selected by the random function, no net change occurs; if an unoccupied cell is selected, its value changes from 0 to 1. The multiplication and dispersal processes are offset by a mortality level that ranges from 0 to 1. Mortality is imposed on each cell by selecting a uniformly distributed random number between 0 and 1; at a mortality of 0.3, for example, a cell's value will change from 1 to 0 if the random number is less than or equal to 0.3.

Fig. 2. A flow chart showing the processes that occur within the cellular automaton model. The introduced population produces two propagules or offspring that disperse randomly within a set distance. If they land in an occupied cell, they die; if they land in an unoccupied cell, they survive. All occupied cells then undergo random mortality before the cycle repeats itself.

GIF Image (15 K)

Individual simulations were continued for 5000 iterations, by which time each simulation had reached equilibrium. Because the model is stochastic, it does not produce the same answer every time; although it approaches similar equilibrial densities, these may differ depending on random fluctuations. I used multiple replicates of each set of conditions to establish general trends. The program reports which cells are occupied at each iteration and the total number of cells occupied, which serves as a surrogate for metapopulation density. I initially explored the consequences of varying mortality rates using 20 replicates of each set of conditions. These simulations suggested that shape effects were more likely at higher mortality rates. I then ran 100 replicates in each hypothetical habitat type at a mortality of 0.3. These simulations included five stream habitat types (simple with 0 nodes and simple or complex with 10 or 20 nodes) and three grid habitat types (40 x 40, 20 x 80, and 10 x 160 cells, respectively).

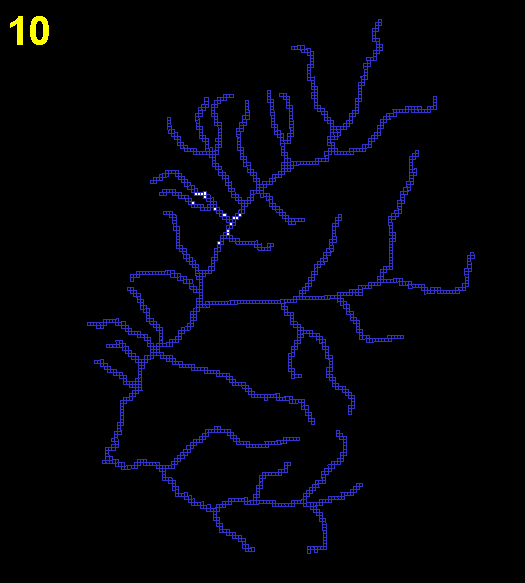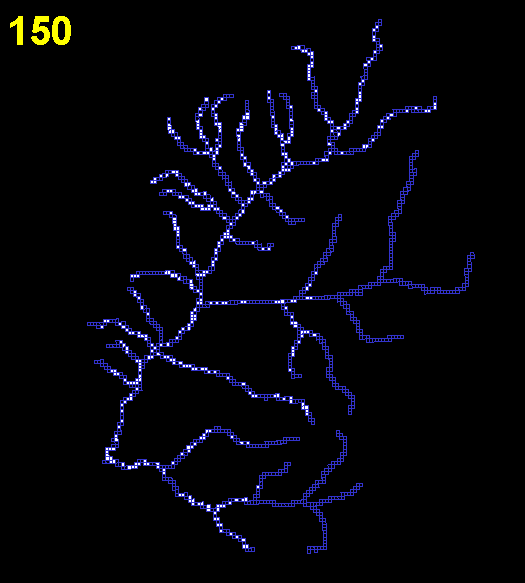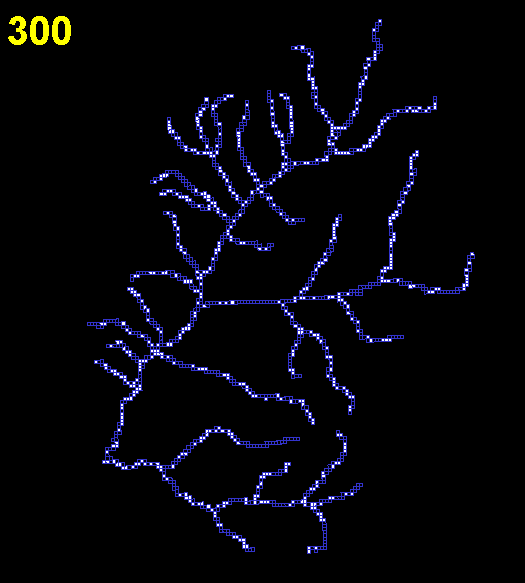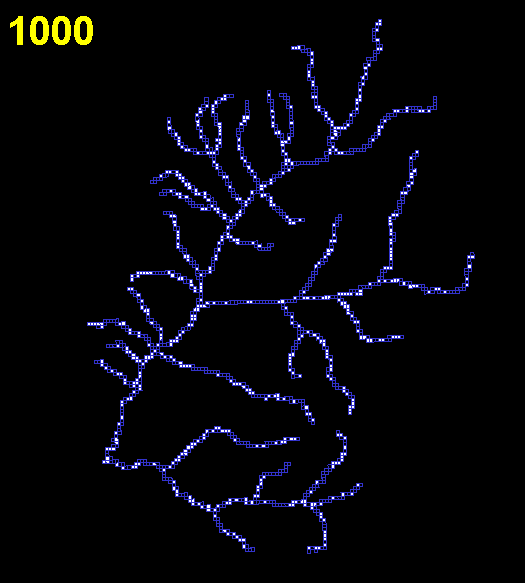
For each hypothetical habitat, I considered the rate at which the simulation reached equilibrium and the total carrying capacity of each cell. The data were summarized using the total number of occupied cells at each time step. To determine an equilibrium value for cellular automaton simulations, I took the mean of the last 500 iterations. Time to equilibrium was defined as the time that elapsed before the total number of occupied cells first exceeded this mean value. A typical sequence of colonization through a real stream network in Wisconsin is shown in Figs. 3 and 4.

Fig. 3. Animated time series simulating colonization of a real stream habitat in Wisconsin by a hypothetical invasive species, as modeled using the cellular automaton model. The number in the upper left corner indicates the number of iterations at which the observation was made. The blue grid outlines habitat cells, and white shading indicates cell occupancy.

GIF Image (73 K)

Fig. 4. Plot showing the total size of the metapopulation of the real stream over time. As can be seen by watching Fig. 3, the species has reached all parts of the stream network by iteration 250; after this there is little net change in abundance, although the occupancies of different cells vary.

GIF Image (13 K)

Reaction-diffusion model

Roughgarden (1986) stated that the theory of the rate of spread of an invasion " ... is quite robust, has been empirically tested, and is about as reliable as theory gets." The theory to which she was referring originated with Fisher's (1937) population-genetic model for the spread of a favorable mutation and was first brought into a specifically ecological context by Skellam (1951). The central prediction, i.e., that the square root of the area occupied by the invading species grows linearly with time, follows from the coupling of a diffusion model with exponential population growth to produce a reaction-diffusion model. Although classical reaction-diffusion models have some shortcomings when applied to real data, because their assumption of a normal rather than a leptokurtic dispersal curve may result in the underestimation of the rate of spread of the invading population (Kot et al. 1996), this inaccuracy is irrelevant to the conclusions of this paper.

I used a simple form of reaction-diffusion model known as Fisher's equation. A full outline of mathematical and programming methods for diffusion models can be found in Press et al. (1992). Reaction-diffusion models have two parts: a diffusion term and a reaction term. Diffusion and reaction occur separately. The reaction term in this instance was a simple logistic population increase:

         Nt+1 = Nt + rNt(1 - (Nt/K)) (1)

where Nt is the population size at time t, r is the intrinsic rate of increase, and K is the carrying capacity (Tilman and Kareiva 1997). I did not include stochastic mortality in the population model. The population parameter r was set at 0.5, and K remained at 500 individuals per cell for all simulations.

The diffusion term used a multidimensional form of the diffusion equation (Press et al. 1992), which in one space dimension is

         u/t = x(Du/x) (2)

where D is the diffusion coefficient, t is time, u is the population size in a given cell, and x is the distance over which diffusion takes place. This equation can be differenced in various ways, the simplest of which (in a single dimension) is

         (ujn+1 - ujn)/t = D(uj+1n - 2ujn + uj-1n)/(x)2 (3)

where D is the diffusion coefficient, uj is the population size at time t, uj+1 and uj-1 indicate population sizes in neighbouring cells, n is the current iteration, t is the time step, and x is the distance over which diffusion takes place. I used this form of the equation because of its computational speed, which is important for simulations this large. Its main drawback is that it is only stable for parameter combinations such that

         2Dt/(x)2 1. (4)

All the simulations used unit habitat cells and a time step of 1, but, because each cell had up to four neighbours, the value of the diffusion coefficient (D) was constrained to less than 0.25.

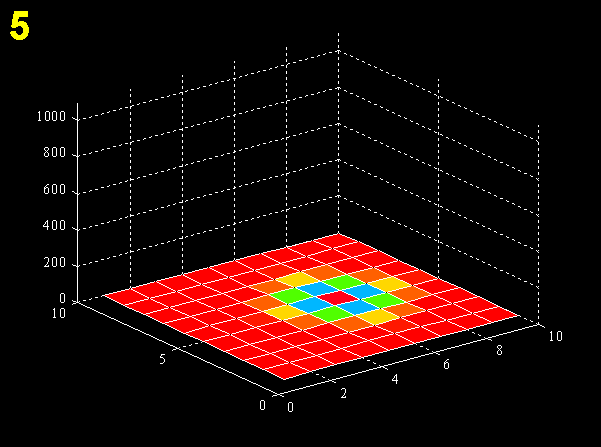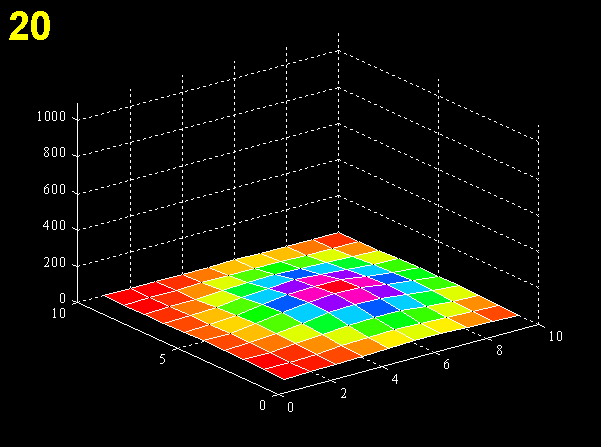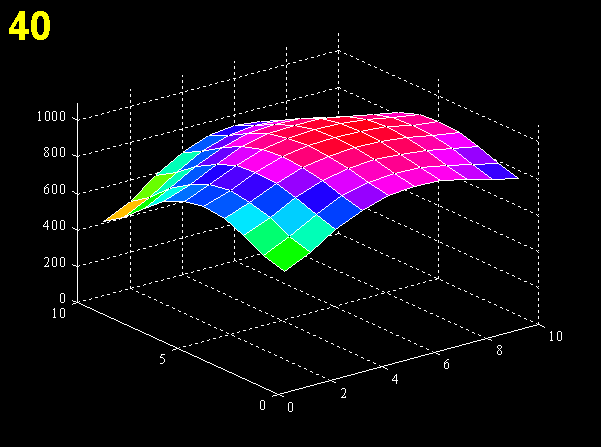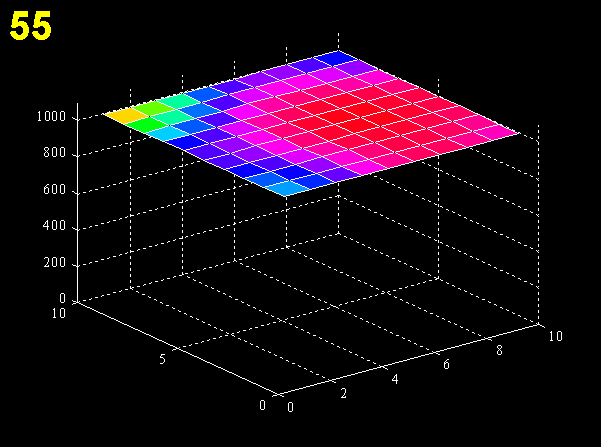
For each cell, the model considers how many neighbors it has and uses the appropriate diffusion term (i.e., for one, two, three, or four neighbors). Neighboring cells in the reaction-diffusion model are defined as those that share two corners; dispersal was permitted only between immediate neighbors. If run to equilibrium, the model will fill all available habitat to carrying capacity (Fig. 5).

Fig. 5. Animated time series simulating colonization of a 10 x 10-degree grid by a hypothetical invasive species, as modeled using a reaction-diffusion process. A population of 100 individuals is introduced at the centre of the grid, and logistic population increase, coupled with diffusion, occurs until the population reaches carrying capacity. The number in the upper left corner indicates the iteration number. The colors correspond to the values of individual cells along a gradient from red through blue and green to yellow and back to red; cells are reshaded at each iteration.

GIF Image (99 K)

The reaction-diffusion model was run in the same hypothetical habitats as the cellular automaton model. In each instance, 100 individuals were introduced into a single cell, and the simulation continued until all the cells in the habitat had reached carrying capacity. The change in total abundance over time was then plotted to give the rate at which the invasive metapopulation increased. Because this model has no stochastic terms, multiple simulations under the same conditions were not necessary. Because there was no mortality term, the final carrying capacity of each habitat was identical.

RESULTS

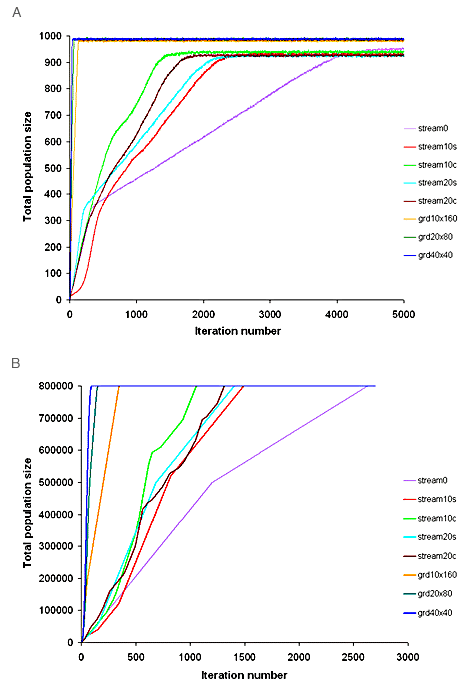
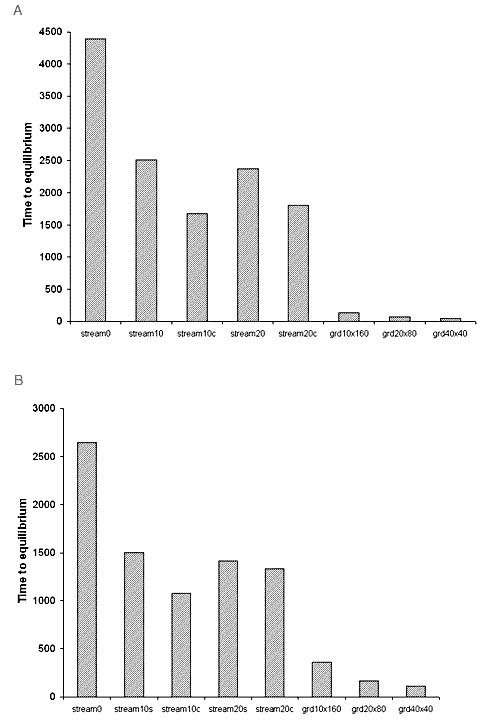
For both the cellular automaton and the reaction-diffusion models, different hypothetical habitats (Fig. 1) were colonized at different rates (Figs. 6 and 7). The populations in the two-dimensional grids were the first to reach equilibrium, followed by those in the branching networks; the linear system was the slowest to be invaded in each instance. The more hierarchically arranged networks were colonized more quickly than the networks with a less nested form but the same number of nodes.

Fig. 6. Rates of occupancy of different hypothetical habitats under the cellular automaton model (A) and the reaction-diffusion model (B). In each graph, streamN denotes a branching habitat with N nodes that can be either simple (s) or complex (c), and grdxxy denotes a square or rectangular habitat with sides of length x and y.

GIF Image (27 K)

Fig. 7. Bar charts showing the differences in time to equilibrium for different hypothetical habitats under each model. Chart A results from the cellular automaton model at a mortality of 0.3; B, from the reaction-diffusion model with a population parameter of 0.5 and a carrying capacity of 500. Please see Fig. 6 for an explanation of the captions on the x axes.

GIF Image (29 K)

The influence of habitat shape on population processes will clearly be less pronounced for populations that have shorter generation times, move farther or faster, or have higher fecundity. As one might expect, the lower mortality rates in the cellular automaton model resulted in more similar colonization rates (Fig. 8).

Fig. 8. Equilibrium abundances attained in hypothetical habitats by the cellular automaton model. The error bars indicate ± one standard deviation in the values of the last 500 iterations (each of these values is an average of 100 simulations). Please see Fig. 6 for an explanation of the captions on the x axis.

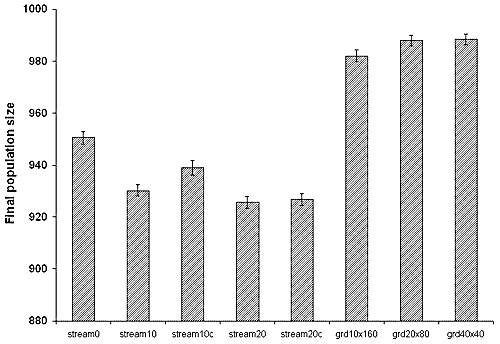
GIF Image (16 K)

Interestingly, the final abundance of metapopulations from the cellular automaton model (as measured by the mean and standard deviation of the last 500 iterations) was significantly different between habitats (Fig. 9). In general, habitats that were colonized more quickly achieved higher eventual abundances of invaders. A test for correlation between time to equilibrium and eventual abundance yielded Kendall's Tau = -0.571 with a significance of p = 0.048 (n = 8). This result was influenced by the unexpectedly high abundance of individuals in the linear system; with this observation removed from the analysis, the value of Kendall's Tau increased to -0.81 (p = 0.007, n = 7).

Fig. 9. Times to equilibrium, expressed as number of time steps, in the 10-node stream network under different mortality conditions. When the random mortality term is set to 0.05, the population occupies its habitat more quickly and reaches a higher carrying capacity than at a mortality of 0.3.

GIF Image (8 K)

DISCUSSION

The results suggest unequivocally that habitat shape is an important determinant of the rate at which an invading population can fill available space. Although these models ignore many real-world factors, they serve as a useful heuristic from which to generate hypotheses. Both modeling methods have been applied successfully in real-world situations (Okubo 1980, Levin 1992, Tilman and Kareiva 1997) and yielded the same intuitively obvious conclusion. Habitats that have a more complex topology allow organisms to move through them at a faster rate, colonize unoccupied spaces more rapidly, and reach carrying capacity more quickly. Consequently, they are more likely than identical habitats of different topologies to be successfully invaded by an introduced species that is well suited to local conditions. The differences in the rates at which organisms can move within and between habitats may in turn create differences in the age structure of populations, depending on which life stages disperse more (Major et al. 1999), and the ultimate size of the population, depending on the local disturbance regime and how quickly empty habitats are recolonized.

The variations in colonization rates among different hypothetical habitats are not a simple consequence of differing degrees of connectivity. Although connectivity is undoubtedly important, the difference in colonization rates between hypothetical networks with identical connectivities but different spatial arrangements (such as the simple and complex networks with 10 nodes) shows that the precise arrangement of cells relative to one another is also important for processes related to dispersal. A more important metric, but one that is harder to quantify, is how branching or hierarchical the system is. Once an increasing population has split into two subpopulations at a node, it then increases at twice the previous rate. Faster colonization is facilitated by habitat configurations that split the population more frequently per unit area. Arrangements with more nodes are colonized more rapidly, but the position of these nodes relative to one another is also important. In real aquatic systems, this implies that more complex river networks will be more vulnerable to invasion than simpler ones; in the terrestrial context, reserve arrangements or the manner in which habitats are fragmented will be a correlate of their susceptibility to invasion.

The current focus in the design of reserves and reserve networks is primarily on proximity and connectivity. The connection of protected areas by corridors (Simberloff et al. 1992, Collinge 2000, Mortberg and Wallentinus 2000) needs to be carefully thought out, particularly in regions where species invasions are common. Increasing the connectivity of reserves will not necessarily be beneficial to the cause of conservation. Habitats that are more complex may be more vulnerable to the spread of invaders, parasites, and pathogens. On the positive side, they may also be more resilient to external perturbations because areas from which organisms are eliminated will be filled more quickly. The results of this study suggest that dispersal and population abundance will be influenced not only by the number of corridors but also by how hierarchical the resulting system is. In aquatic systems, where branching is more obvious, control of invasive species may be made more efficient by taking habitat complexity and topology into account; managers will need to move more rapidly to contain invasive species in habitats with complex topologies, where they will spread more quickly and attain higher abundances, than in simpler catchments where the spread of the species is likely to be slower and the final impact smaller. Similarly, it may be easier to fragment complex habitats deliberately without loss of functionality by breaking key connections, thus limiting the spread of invaders through the system.

Adequate tests of these predictions are likely be difficult in real situations, where differences in the local environment between habitat fragments may obscure shape effects. The model world differs from the real world in many ways, most importantly in the simplifying assumptions that the models make about habitat homogeneity and constant rates of movement. Stream environments will probably be less homogeneous within highly branching networks than within relatively linear systems because of differences in the rates of change in stream size. In addition, the number of tributaries feeding into a stream is affected by superficial geomorphology, which also affects biotic communities. Large differences in tributary ramifications are unlikely to occur in highly similar habitats. Real-world populations typically show considerable variation in mortality rates; abiotic disturbances, human interventions, and biotic factors such as competition and predation are seldom constant in time or space. Similarly, animals typically disperse more at certain times of the year than at others. The best test systems will probably be those involving hardy, ubiquitous invaders that move along stream networks or riparian corridors; possible study species include crayfish and rabbits.

SPECULATION

As with other explicitly spatial phenomena, the relative differences generated by shape effects are likely to depend on scale. In real-world situations where there is a choice between different reserve designs, this kind of simulation approach may provide some valuable insights into the likely success of invasions and reintroductions. Dispersal and reproduction models that more closely imitate the spread of real animals in real habitats need to be developed and tested in real and hypothetical reserves of different designs. We can envisage that most reserve designs will be a compromise between risk and security, with smaller reserves being more vulnerable to disruption and larger reserves more robust. Conversely, control of invasive species will be more difficult in larger areas. Given more information on the vulnerability of habitats to invasion, it may be possible at some point to calculate an optimal or minimum reserve size, shape, and connectivity for individual species to balance internally and externally driven processes. In the meantime, the most secure long-term strategy is probably to maintain reserves of different sizes and shapes (including some very isolated areas) and monitor them closely.

The shape-dependency of dispersal and reproduction processes over large areas and long time scales may also have important consequences for evolutionary processes such as speciation and extinction. Speciation is more likely in habitats where genetic isolation is more readily achieved. It stands to reason that the likelihood of an isolating event would be higher in longer, thinner habitats with fewer connections. Extinctions may also be more likely in less complex habitats; for example, the effects of global warming on cold-water fish species may be more evident in high-altitude streams that have fewer branches.

RESPONSES TO THIS ARTICLE

Responses to this article are invited. If accepted for publication, your response will be hyperlinked to the article. To submit a comment, follow this link. To read comments already accepted, follow this link.

Acknowledgments:

I am grateful to Steve Carpenter and two anonymous referees for comments on an earlier draft of this manuscript. This work was funded by a David H. Smith postdoctoral fellowship from The Nature Conservancy. This is publication DHS2001-1 of the David H. Smith Conservation Research Fellowship Program.

APPENDIX 1

Append1.zip contains Matlab version 5.3 routines for both of the models that are presented in this paper. The files are in ASCII text format. Use the links below to view the files online.

The cellular automaton model
Cellaut.m contains matlab code for the cellular automaton model. It is currently set to run 20 iterations, each of 5000 steps, under the given conditions.

The reaction-diffusion model
This program consists of six separate .m files. Diffuse.m is the master routine. Diffuse1.m to Diffuse4.m are diffusion routines that are called by Diffuse.m for cells with one to four neighbours. Reproduce.m contains the logistic population increase term. This model provides a framework into which any set of coordinates can be read. It requires that parameter restrictions are observed (as outlined in the methods section) and that the distance between cells is unity. Grids based on real coordinates can easily be reformatted to give unit coordinate spacing; simply subtract the minimum x and y coordinates and divide by the inter-cell distance. If this is done in a spreadsheet, keeping the key of matching coordinate pairs, the results can readily be matched to the original coordinates and plotted in ‘real’ space. Note that dispersal can only occur between adjacent cells; there is no long-distance dispersal to unconnected habitat patches. In both cases you will need to change the working directory (from which input files are read, and to which the results file is sent) by altering the line ‘cd d:\myfolder’ to ‘cd yourworkingdiskdrive:\yourfolderofchoice’. (e.g. change ‘d:\myfolder’ to d:\models\diffusion’). You may also need to add your folder to Matlab’s directory using the ‘set path’ option in the Matlab command window.

cellaut.m
% Cellular automaton model - stochastic dispersal, reproduction and mortality
% Written by Graeme Cumming, November 2000

% set the working directory for your own machine
cd e:\cellaut2

% these commands read in x,y coords from file myfile.txt
fid = fopen ('stream0.txt','r');
[xcoord,ycoord] = textread ('stream0.txt','%f %f');
status = fclose (fid);
count = size (xcoord);

% initialise the variables for the program
cell = zeros (count);
cell2 = zeros (count);
cell (500) = 1; %starting value
dispdist = 3; %dispersal distance in m
inc = 2; %number of 'offspring' per iteration
mortality = 300; %death rate / 1000
area = ceil (3.141592654*(dispdist^2)); %max possible number of neighbours
neighbour = zeros (count,area);

reps = 5000;

%first we write a matrix containing identifiers of all cells in dispersal range
for x = 1:count
   match = 1;
      for i = 1:count
          distance = sqrt(((xcoord(x)-xcoord(i))^2)+((ycoord(x)-ycoord(i))^2));
            if distance <= dispdist
              match = match + 1;
              neighbour(x,1) = neighbour(x,1)+1;
              neighbour(x,match) = i;
      end;
        end;
end;

%now begins the main loop of the program

for z = 1:100

cell = zeros (count);
cell2 = zeros (count);
cell (500) = 1;
results = zeros (10000,1);

for r = 1:reps

%disperse
for j = 1:count
   if cell(j) == 1
     cell2(j) = 1;
     for m = 1:inc
             rnum = rand * neighbour(j,1);
             p = ceil(rnum);
                     if p==1
                     p = 2;
                     end;
             plusone_id = neighbour(j,p);
             cell2(plusone_id) = 1;
     end;
       end;
end;

cell = cell2;
cell2 = zeros (count);

for k = 1:count
    if round(rand*1000) < mortality
       cell(k) = 0;
       end;
end;

%results
tally = sum(cell);
results(r,1) = tally;

if tally==0
    break
end;

disp (r);

end;
%^ ends the main loop

if z == 1
   final = results;
end;
if z > 1
   final = cat(2,final,results);
end;

end;

save ('results1.txt','final','-ascii');

diffuse.m
% Program Diffuse
% Written by Graeme Cumming, October 2000

% Program aim is to provide a general reaction-diffusion modelling framework
% Coordinates of study system are read in from a text file 'coords'
% A matrix 'proxim' is then written that holds the number of adjacent cells
% and which cells are adjacent, for each cell

% Diffusion occurs in one of three ways depending on # adjacent cells
%                1 adjacent cell: simple exchange
%                2 adjacent cells: reaction-diffusion in one plane
%                3 adjacent cells: r-d between 3 peripheral and one central cells
%                4 adjacent cells: two dimensional r-d

% After diffusion is completed for each cell, populations increase
% Population increase is determined by a logistic growth equation

% start by setting the home directory
cd e:\diffusn\streams\

% these commands read in x,y coords from columns in file tlake1.txt
fid = fopen ('stream0.txt','r');
[xcoord,ycoord] = textread ('stream0.txt','%f %f');
status = fclose (fid);
count = size (xcoord);
% the coordinate data are now in two vectors, 'xcoord' and 'ycoord'
% 'count' holds the number of coordinates

global adjacent
         adjacent = zeros (count,5);
% reserve space for number of and identifiers of adjacent cells
global current;
         current = zeros (count);
% the vector 'current' holds current n for each cell at time t
global cplus1;
         cplus1 = zeros (count);
% 'cplus1' holds n for each cell at time step t+1
global D;
         D = 0.1;
% D is the diffusion coefficient
% for the current diffuse2 it must be <= .5
global cellwidth;
cellwidth = 1;
% the real-world width of the cells, which are presumed to be squares

% now to calculate the proximity key
for j = 1:count
   adjacent(j,1) = 0;
   for i = 1:count
      distance = sqrt(((xcoord(i)-xcoord(j))^2)+((ycoord(i)-ycoord(j))^2));
      if distance == cellwidth
         adjacent(j,1) = adjacent(j,1) + 1;
         celltofill = adjacent(j,1) + 1;
         adjacent(j,celltofill) = i;
      end;
   end;
end;
% the 5 x count matrix has number of neighbours and up to 4 cell identifiers
% for each cell in the analysis


% seed the 500th cell with 100 individuals
current(500) = 100;

% next, the main diffusion loop

iterations = 3000;
step = 1;
%results = current;
num = 1;
results = zeros (count);

for k = 1:iterations
% number of diffusion iterations

% the following calls different diffusion routines
for j = 1:count
   switch (adjacent(j,1))
        case (1)
              diffuse1 (j);
        case (2)
              diffuse2 (j);
        case (3)
              diffuse3 (j);
        case (4)
              diffuse4 (j);
        otherwise
             disp ('ERROR - not finding neighbours');
   end;
reproduce (j);
end;

current = cplus1;

% save the results every n steps
if k/step == floor(k/step)
   % results = cat(2,results,cplus1);
   results(num) = sum(cplus1);
   num = num+1;
end;

disp (k)

if k/3000 == floor(k/3000)
     save ('results1.txt','results','-ascii');
end;

end;

diffuse1.m to diffuse4.m

diffuse1.m
function [diff1] = diffuse1(j)

% diffusion into the end-cell

global cplus1;
global adjacent;
global current;
global D;
global cellwidth;

neighbour = adjacent(j,2);
unj = current(neighbour);
% unj is the current value of the cell next to the end-point

endcell = current(j);

if endcell <= unj
   cplus1(j) = endcell + (unj-endcell)/2;
end;

if endcell > unj
   cplus1(j) = endcell - (endcell-unj)/2;
end;

diffuse2.m
function [diff2] = diffuse2(j)

global cplus1;
global current;
global adjacent;
global D;
global cellwidth;

unj = current(j);
currnt1 = adjacent(j,2);
unjplus1 = current (currnt1);
currnt2 = adjacent (j,3);
unjminus1 = current (currnt2);

RHS = (((unjplus1 - (2*unj) + unjminus1))/(cellwidth^2))*D;
% cellwidth = delta x

cplus1(j) = RHS + unj;

diffuse3.m
function [diff3] = diffuse3(j)

global cplus1;
global current;
global adjacent;
global D;
global cellwidth;

unj = current(j);

c1 = adjacent(j,2);
c2 = adjacent(j,3);
c3 = adjacent(j,4);

% c1-c3 are the identifiers of the 3 neighbouring cells

currnt1 = current(c1);
currnt2 = current(c2);
currnt3 = current(c3);

% currnt1-currnt3 are the values of the 3 neighbouring cells

RHS = (((currnt1 - (3*unj) + currnt2 + currnt3))/(cellwidth^2))*D;

% cellwidth = delta x = 1; delta t is 1
% the flow is now three-way

cplus1(j) = RHS + unj;

diffuse4.m
function [diff4] = diffuse4(j)

global cplus1;
global current;
global adjacent;
global D;
global cellwidth;

unj = current(j);

c1 = adjacent(j,2);
c2 = adjacent(j,3);
c3 = adjacent(j,4);
c4 = adjacent(j,5);

% c1-c4 are the identifiers of the 4 neighbouring cells

currnt1 = current(c1);
currnt2 = current(c2);
currnt3 = current(c3);
currnt4 = current(c4);

% currnt1-currnt4 are the values of the 4 neighbouring cells

RHS = (((currnt1 - (4*unj) + currnt2 + currnt3 + currnt4))/(cellwidth^2))*D;

% cellwidth = delta x = 1; delta t is also 1
% the flow is now four-way

cplus1(j) = RHS + unj;

reproduce.m
function [shithappens] = reproduce (j)

% exponential population increase

global cplus1;

N = cplus1(j);
r = .5;
K = 500;

babies = r*N*(1-(N/K));

%fate = rand;
% fate is a random number between 0 and 1
% corpses = ((fate/1)*N)/2;
% a random proportion of the population, not exceeding 50%, dies at every iteration

corpses = 0;

cplus1(j) = cplus1(j) + babies - corpses;

 

 

APPENDIX 2

Append2.zip contains the hypothetical habitat files used in the analysis. Each pair of (x,y) coordinates specifies the centre of a habitat cell. The files are in ASCII text format; PC users can open them through Excel or view them directly in Notepad. 

grd10x160
1	1
2	1
3	1
4	1
5	1
6	1
7	1
8	1
9	1
10	1
11	1
12	1
13	1
14	1
15	1
16	1
17	1
18	1
19	1
20	1
21	1
22	1
23	1
24	1
25	1
26	1
27	1
28	1
29	1
30	1
31	1
32	1
33	1
34	1
35	1
36	1
37	1
38	1
39	1
40	1
41	1
42	1
43	1
44	1
45	1
46	1
47	1
48	1
49	1
50	1
51	1
52	1
53	1
54	1
55	1
56	1
57	1
58	1
59	1
60	1
61	1
62	1
63	1
64	1
65	1
66	1
67	1
68	1
69	1
70	1
71	1
72	1
73	1
74	1
75	1
76	1
77	1
78	1
79	1
80	1
81	1
82	1
83	1
84	1
85	1
86	1
87	1
88	1
89	1
90	1
91	1
92	1
93	1
94	1
95	1
96	1
97	1
98	1
99	1
100	1
101	1
102	1
103	1
104	1
105	1
106	1
107	1
108	1
109	1
110	1
111	1
112	1
113	1
114	1
115	1
116	1
117	1
118	1
119	1
120	1
121	1
122	1
123	1
124	1
125	1
126	1
127	1
128	1
129	1
130	1
131	1
132	1
133	1
134	1
135	1
136	1
137	1
138	1
139	1
140	1
141	1
142	1
143	1
144	1
145	1
146	1
147	1
148	1
149	1
150	1
151	1
152	1
153	1
154	1
155	1
156	1
157	1
158	1
159	1
160	1
1	2
2	2
3	2
4	2
5	2
6	2
7	2
8	2
9	2
10	2
11	2
12	2
13	2
14	2
15	2
16	2
17	2
18	2
19	2
20	2
21	2
22	2
23	2
24	2
25	2
26	2
27	2
28	2
29	2
30	2
31	2
32	2
33	2
34	2
35	2
36	2
37	2
38	2
39	2
40	2
41	2
42	2
43	2
44	2
45	2
46	2
47	2
48	2
49	2
50	2
51	2
52	2
53	2
54	2
55	2
56	2
57	2
58	2
59	2
60	2
61	2
62	2
63	2
64	2
65	2
66	2
67	2
68	2
69	2
70	2
71	2
72	2
73	2
74	2
75	2
76	2
77	2
78	2
79	2
80	2
81	2
82	2
83	2
84	2
85	2
86	2
87	2
88	2
89	2
90	2
91	2
92	2
93	2
94	2
95	2
96	2
97	2
98	2
99	2
100	2
101	2
102	2
103	2
104	2
105	2
106	2
107	2
108	2
109	2
110	2
111	2
112	2
113	2
114	2
115	2
116	2
117	2
118	2
119	2
120	2
121	2
122	2
123	2
124	2
125	2
126	2
127	2
128	2
129	2
130	2
131	2
132	2
133	2
134	2
135	2
136	2
137	2
138	2
139	2
140	2
141	2
142	2
143	2
144	2
145	2
146	2
147	2
148	2
149	2
150	2
151	2
152	2
153	2
154	2
155	2
156	2
157	2
158	2
159	2
160	2
1	3
2	3
3	3
4	3
5	3
6	3
7	3
8	3
9	3
10	3
11	3
12	3
13	3
14	3
15	3
16	3
17	3
18	3
19	3
20	3
21	3
22	3
23	3
24	3
25	3
26	3
27	3
28	3
29	3
30	3
31	3
32	3
33	3
34	3
35	3
36	3
37	3
38	3
39	3
40	3
41	3
42	3
43	3
44	3
45	3
46	3
47	3
48	3
49	3
50	3
51	3
52	3
53	3
54	3
55	3
56	3
57	3
58	3
59	3
60	3
61	3
62	3
63	3
64	3
65	3
66	3
67	3
68	3
69	3
70	3
71	3
72	3
73	3
74	3
75	3
76	3
77	3
78	3
79	3
80	3
81	3
82	3
83	3
84	3
85	3
86	3
87	3
88	3
89	3
90	3
91	3
92	3
93	3
94	3
95	3
96	3
97	3
98	3
99	3
100	3
101	3
102	3
103	3
104	3
105	3
106	3
107	3
108	3
109	3
110	3
111	3
112	3
113	3
114	3
115	3
116	3
117	3
118	3
119	3
120	3
121	3
122	3
123	3
124	3
125	3
126	3
127	3
128	3
129	3
130	3
131	3
132	3
133	3
134	3
135	3
136	3
137	3
138	3
139	3
140	3
141	3
142	3
143	3
144	3
145	3
146	3
147	3
148	3
149	3
150	3
151	3
152	3
153	3
154	3
155	3
156	3
157	3
158	3
159	3
160	3
1	4
2	4
3	4
4	4
5	4
6	4
7	4
8	4
9	4
10	4
11	4
12	4
13	4
14	4
15	4
16	4
17	4
18	4
19	4
20	4
21	4
22	4
23	4
24	4
25	4
26	4
27	4
28	4
29	4
30	4
31	4
32	4
33	4
34	4
35	4
36	4
37	4
38	4
39	4
40	4
41	4
42	4
43	4
44	4
45	4
46	4
47	4
48	4
49	4
50	4
51	4
52	4
53	4
54	4
55	4
56	4
57	4
58	4
59	4
60	4
61	4
62	4
63	4
64	4
65	4
66	4
67	4
68	4
69	4
70	4
71	4
72	4
73	4
74	4
75	4
76	4
77	4
78	4
79	4
80	4
81	4
82	4
83	4
84	4
85	4
86	4
87	4
88	4
89	4
90	4
91	4
92	4
93	4
94	4
95	4
96	4
97	4
98	4
99	4
100	4
101	4
102	4
103	4
104	4
105	4
106	4
107	4
108	4
109	4
110	4
111	4
112	4
113	4
114	4
115	4
116	4
117	4
118	4
119	4
120	4
121	4
122	4
123	4
124	4
125	4
126	4
127	4
128	4
129	4
130	4
131	4
132	4
133	4
134	4
135	4
136	4
137	4
138	4
139	4
140	4
141	4
142	4
143	4
144	4
145	4
146	4
147	4
148	4
149	4
150	4
151	4
152	4
153	4
154	4
155	4
156	4
157	4
158	4
159	4
160	4
1	5
2	5
3	5
4	5
5	5
6	5
7	5
8	5
9	5
10	5
11	5
12	5
13	5
14	5
15	5
16	5
17	5
18	5
19	5
20	5
21	5
22	5
23	5
24	5
25	5
26	5
27	5
28	5
29	5
30	5
31	5
32	5
33	5
34	5
35	5
36	5
37	5
38	5
39	5
40	5
41	5
42	5
43	5
44	5
45	5
46	5
47	5
48	5
49	5
50	5
51	5
52	5
53	5
54	5
55	5
56	5
57	5
58	5
59	5
60	5
61	5
62	5
63	5
64	5
65	5
66	5
67	5
68	5
69	5
70	5
71	5
72	5
73	5
74	5
75	5
76	5
77	5
78	5
79	5
80	5
81	5
82	5
83	5
84	5
85	5
86	5
87	5
88	5
89	5
90	5
91	5
92	5
93	5
94	5
95	5
96	5
97	5
98	5
99	5
100	5
101	5
102	5
103	5
104	5
105	5
106	5
107	5
108	5
109	5
110	5
111	5
112	5
113	5
114	5
115	5
116	5
117	5
118	5
119	5
120	5
121	5
122	5
123	5
124	5
125	5
126	5
127	5
128	5
129	5
130	5
131	5
132	5
133	5
134	5
135	5
136	5
137	5
138	5
139	5
140	5
141	5
142	5
143	5
144	5
145	5
146	5
147	5
148	5
149	5
150	5
151	5
152	5
153	5
154	5
155	5
156	5
157	5
158	5
159	5
160	5
1	6
2	6
3	6
4	6
5	6
6	6
7	6
8	6
9	6
10	6
11	6
12	6
13	6
14	6
15	6
16	6
17	6
18	6
19	6
20	6
21	6
22	6
23	6
24	6
25	6
26	6
27	6
28	6
29	6
30	6
31	6
32	6
33	6
34	6
35	6
36	6
37	6
38	6
39	6
40	6
41	6
42	6
43	6
44	6
45	6
46	6
47	6
48	6
49	6
50	6
51	6
52	6
53	6
54	6
55	6
56	6
57	6
58	6
59	6
60	6
61	6
62	6
63	6
64	6
65	6
66	6
67	6
68	6
69	6
70	6
71	6
72	6
73	6
74	6
75	6
76	6
77	6
78	6
79	6
80	6
81	6
82	6
83	6
84	6
85	6
86	6
87	6
88	6
89	6
90	6
91	6
92	6
93	6
94	6
95	6
96	6
97	6
98	6
99	6
100	6
101	6
102	6
103	6
104	6
105	6
106	6
107	6
108	6
109	6
110	6
111	6
112	6
113	6
114	6
115	6
116	6
117	6
118	6
119	6
120	6
121	6
122	6
123	6
124	6
125	6
126	6
127	6
128	6
129	6
130	6
131	6
132	6
133	6
134	6
135	6
136	6
137	6
138	6
139	6
140	6
141	6
142	6
143	6
144	6
145	6
146	6
147	6
148	6
149	6
150	6
151	6
152	6
153	6
154	6
155	6
156	6
157	6
158	6
159	6
160	6
1	7
2	7
3	7
4	7
5	7
6	7
7	7
8	7
9	7
10	7
11	7
12	7
13	7
14	7
15	7
16	7
17	7
18	7
19	7
20	7
21	7
22	7
23	7
24	7
25	7
26	7
27	7
28	7
29	7
30	7
31	7
32	7
33	7
34	7
35	7
36	7
37	7
38	7
39	7
40	7
41	7
42	7
43	7
44	7
45	7
46	7
47	7
48	7
49	7
50	7
51	7
52	7
53	7
54	7
55	7
56	7
57	7
58	7
59	7
60	7
61	7
62	7
63	7
64	7
65	7
66	7
67	7
68	7
69	7
70	7
71	7
72	7
73	7
74	7
75	7
76	7
77	7
78	7
79	7
80	7
81	7
82	7
83	7
84	7
85	7
86	7
87	7
88	7
89	7
90	7
91	7
92	7
93	7
94	7
95	7
96	7
97	7
98	7
99	7
100	7
101	7
102	7
103	7
104	7
105	7
106	7
107	7
108	7
109	7
110	7
111	7
112	7
113	7
114	7
115	7
116	7
117	7
118	7
119	7
120	7
121	7
122	7
123	7
124	7
125	7
126	7
127	7
128	7
129	7
130	7
131	7
132	7
133	7
134	7
135	7
136	7
137	7
138	7
139	7
140	7
141	7
142	7
143	7
144	7
145	7
146	7
147	7
148	7
149	7
150	7
151	7
152	7
153	7
154	7
155	7
156	7
157	7
158	7
159	7
160	7
1	8
2	8
3	8
4	8
5	8
6	8
7	8
8	8
9	8
10	8
11	8
12	8
13	8
14	8
15	8
16	8
17	8
18	8
19	8
20	8
21	8
22	8
23	8
24	8
25	8
26	8
27	8
28	8
29	8
30	8
31	8
32	8
33	8
34	8
35	8
36	8
37	8
38	8
39	8
40	8
41	8
42	8
43	8
44	8
45	8
46	8
47	8
48	8
49	8
50	8
51	8
52	8
53	8
54	8
55	8
56	8
57	8
58	8
59	8
60	8
61	8
62	8
63	8
64	8
65	8
66	8
67	8
68	8
69	8
70	8
71	8
72	8
73	8
74	8
75	8
76	8
77	8
78	8
79	8
80	8
81	8
82	8
83	8
84	8
85	8
86	8
87	8
88	8
89	8
90	8
91	8
92	8
93	8
94	8
95	8
96	8
97	8
98	8
99	8
100	8
101	8
102	8
103	8
104	8
105	8
106	8
107	8
108	8
109	8
110	8
111	8
112	8
113	8
114	8
115	8
116	8
117	8
118	8
119	8
120	8
121	8
122	8
123	8
124	8
125	8
126	8
127	8
128	8
129	8
130	8
131	8
132	8
133	8
134	8
135	8
136	8
137	8
138	8
139	8
140	8
141	8
142	8
143	8
144	8
145	8
146	8
147	8
148	8
149	8
150	8
151	8
152	8
153	8
154	8
155	8
156	8
157	8
158	8
159	8
160	8
1	9
2	9
3	9
4	9
5	9
6	9
7	9
8	9
9	9
10	9
11	9
12	9
13	9
14	9
15	9
16	9
17	9
18	9
19	9
20	9
21	9
22	9
23	9
24	9
25	9
26	9
27	9
28	9
29	9
30	9
31	9
32	9
33	9
34	9
35	9
36	9
37	9
38	9
39	9
40	9
41	9
42	9
43	9
44	9
45	9
46	9
47	9
48	9
49	9
50	9
51	9
52	9
53	9
54	9
55	9
56	9
57	9
58	9
59	9
60	9
61	9
62	9
63	9
64	9
65	9
66	9
67	9
68	9
69	9
70	9
71	9
72	9
73	9
74	9
75	9
76	9
77	9
78	9
79	9
80	9
81	9
82	9
83	9
84	9
85	9
86	9
87	9
88	9
89	9
90	9
91	9
92	9
93	9
94	9
95	9
96	9
97	9
98	9
99	9
100	9
101	9
102	9
103	9
104	9
105	9
106	9
107	9
108	9
109	9
110	9
111	9
112	9
113	9
114	9
115	9
116	9
117	9
118	9
119	9
120	9
121	9
122	9
123	9
124	9
125	9
126	9
127	9
128	9
129	9
130	9
131	9
132	9
133	9
134	9
135	9
136	9
137	9
138	9
139	9
140	9
141	9
142	9
143	9
144	9
145	9
146	9
147	9
148	9
149	9
150	9
151	9
152	9
153	9
154	9
155	9
156	9
157	9
158	9
159	9
160	9
1	10
2	10
3	10
4	10
5	10
6	10
7	10
8	10
9	10
10	10
11	10
12	10
13	10
14	10
15	10
16	10
17	10
18	10
19	10
20	10
21	10
22	10
23	10
24	10
25	10
26	10
27	10
28	10
29	10
30	10
31	10
32	10
33	10
34	10
35	10
36	10
37	10
38	10
39	10
40	10
41	10
42	10
43	10
44	10
45	10
46	10
47	10
48	10
49	10
50	10
51	10
52	10
53	10
54	10
55	10
56	10
57	10
58	10
59	10
60	10
61	10
62	10
63	10
64	10
65	10
66	10
67	10
68	10
69	10
70	10
71	10
72	10
73	10
74	10
75	10
76	10
77	10
78	10
79	10
80	10
81	10
82	10
83	10
84	10
85	10
86	10
87	10
88	10
89	10
90	10
91	10
92	10
93	10
94	10
95	10
96	10
97	10
98	10
99	10
100	10
101	10
102	10
103	10
104	10
105	10
106	10
107	10
108	10
109	10
110	10
111	10
112	10
113	10
114	10
115	10
116	10
117	10
118	10
119	10
120	10
121	10
122	10
123	10
124	10
125	10
126	10
127	10
128	10
129	10
130	10
131	10
132	10
133	10
134	10
135	10
136	10
137	10
138	10
139	10
140	10
141	10
142	10
143	10
144	10
145	10
146	10
147	10
148	10
149	10
150	10
151	10
152	10
153	10
154	10
155	10
156	10
157	10
158	10
159	10
160	10


grd20x80
1	1
2	1
3	1
4	1
5	1
6	1
7	1
8	1
9	1
10	1
11	1
12	1
13	1
14	1
15	1
16	1
17	1
18	1
19	1
20	1
1	2
2	2
3	2
4	2
5	2
6	2
7	2
8	2
9	2
10	2
11	2
12	2
13	2
14	2
15	2
16	2
17	2
18	2
19	2
20	2
1	3
2	3
3	3
4	3
5	3
6	3
7	3
8	3
9	3
10	3
11	3
12	3
13	3
14	3
15	3
16	3
17	3
18	3
19	3
20	3
1	4
2	4
3	4
4	4
5	4
6	4
7	4
8	4
9	4
10	4
11	4
12	4
13	4
14	4
15	4
16	4
17	4
18	4
19	4
20	4
1	5
2	5
3	5
4	5
5	5
6	5
7	5
8	5
9	5
10	5
11	5
12	5
13	5
14	5
15	5
16	5
17	5
18	5
19	5
20	5
1	6
2	6
3	6
4	6
5	6
6	6
7	6
8	6
9	6
10	6
11	6
12	6
13	6
14	6
15	6
16	6
17	6
18	6
19	6
20	6
1	7
2	7
3	7
4	7
5	7
6	7
7	7
8	7
9	7
10	7
11	7
12	7
13	7
14	7
15	7
16	7
17	7
18	7
19	7
20	7
1	8
2	8
3	8
4	8
5	8
6	8
7	8
8	8
9	8
10	8
11	8
12	8
13	8
14	8
15	8
16	8
17	8
18	8
19	8
20	8
1	9
2	9
3	9
4	9
5	9
6	9
7	9
8	9
9	9
10	9
11	9
12	9
13	9
14	9
15	9
16	9
17	9
18	9
19	9
20	9
1	10
2	10
3	10
4	10
5	10
6	10
7	10
8	10
9	10
10	10
11	10
12	10
13	10
14	10
15	10
16	10
17	10
18	10
19	10
20	10
1	11
2	11
3	11
4	11
5	11
6	11
7	11
8	11
9	11
10	11
11	11
12	11
13	11
14	11
15	11
16	11
17	11
18	11
19	11
20	11
1	12
2	12
3	12
4	12
5	12
6	12
7	12
8	12
9	12
10	12
11	12
12	12
13	12
14	12
15	12
16	12
17	12
18	12
19	12
20	12
1	13
2	13
3	13
4	13
5	13
6	13
7	13
8	13
9	13
10	13
11	13
12	13
13	13
14	13
15	13
16	13
17	13
18	13
19	13
20	13
1	14
2	14
3	14
4	14
5	14
6	14
7	14
8	14
9	14
10	14
11	14
12	14
13	14
14	14
15	14
16	14
17	14
18	14
19	14
20	14
1	15
2	15
3	15
4	15
5	15
6	15
7	15
8	15
9	15
10	15
11	15
12	15
13	15
14	15
15	15
16	15
17	15
18	15
19	15
20	15
1	16
2	16
3	16
4	16
5	16
6	16
7	16
8	16
9	16
10	16
11	16
12	16
13	16
14	16
15	16
16	16
17	16
18	16
19	16
20	16
1	17
2	17
3	17
4	17
5	17
6	17
7	17
8	17
9	17
10	17
11	17
12	17
13	17
14	17
15	17
16	17
17	17
18	17
19	17
20	17
1	18
2	18
3	18
4	18
5	18
6	18
7	18
8	18
9	18
10	18
11	18
12	18
13	18
14	18
15	18
16	18
17	18
18	18
19	18
20	18
1	19
2	19
3	19
4	19
5	19
6	19
7	19
8	19
9	19
10	19
11	19
12	19
13	19
14	19
15	19
16	19
17	19
18	19
19	19
20	19
1	20
2	20
3	20
4	20
5	20
6	20
7	20
8	20
9	20
10	20
11	20
12	20
13	20
14	20
15	20
16	20
17	20
18	20
19	20
20	20
1	21
2	21
3	21
4	21
5	21
6	21
7	21
8	21
9	21
10	21
11	21
12	21
13	21
14	21
15	21
16	21
17	21
18	21
19	21
20	21
1	22
2	22
3	22
4	22
5	22
6	22
7	22
8	22
9	22
10	22
11	22
12	22
13	22
14	22
15	22
16	22
17	22
18	22
19	22
20	22
1	23
2	23
3	23
4	23
5	23
6	23
7	23
8	23
9	23
10	23
11	23
12	23
13	23
14	23
15	23
16	23
17	23
18	23
19	23
20	23
1	24
2	24
3	24
4	24
5	24
6	24
7	24
8	24
9	24
10	24
11	24
12	24
13	24
14	24
15	24
16	24
17	24
18	24
19	24
20	24
1	25
2	25
3	25
4	25
5	25
6	25
7	25
8	25
9	25
10	25
11	25
12	25
13	25
14	25
15	25
16	25
17	25
18	25
19	25
20	25
1	26
2	26
3	26
4	26
5	26
6	26
7	26
8	26
9	26
10	26
11	26
12	26
13	26
14	26
15	26
16	26
17	26
18	26
19	26
20	26
1	27
2	27
3	27
4	27
5	27
6	27
7	27
8	27
9	27
10	27
11	27
12	27
13	27
14	27
15	27
16	27
17	27
18	27
19	27
20	27
1	28
2	28
3	28
4	28
5	28
6	28
7	28
8	28
9	28
10	28
11	28
12	28
13	28
14	28
15	28
16	28
17	28
18	28
19	28
20	28
1	29
2	29
3	29
4	29
5	29
6	29
7	29
8	29
9	29
10	29
11	29
12	29
13	29
14	29
15	29
16	29
17	29
18	29
19	29
20	29
1	30
2	30
3	30
4	30
5	30
6	30
7	30
8	30
9	30
10	30
11	30
12	30
13	30
14	30
15	30
16	30
17	30
18	30
19	30
20	30
1	31
2	31
3	31
4	31
5	31
6	31
7	31
8	31
9	31
10	31
11	31
12	31
13	31
14	31
15	31
16	31
17	31
18	31
19	31
20	31
1	32
2	32
3	32
4	32
5	32
6	32
7	32
8	32
9	32
10	32
11	32
12	32
13	32
14	32
15	32
16	32
17	32
18	32
19	32
20	32
1	33
2	33
3	33
4	33
5	33
6	33
7	33
8	33
9	33
10	33
11	33
12	33
13	33
14	33
15	33
16	33
17	33
18	33
19	33
20	33
1	34
2	34
3	34
4	34
5	34
6	34
7	34
8	34
9	34
10	34
11	34
12	34
13	34
14	34
15	34
16	34
17	34
18	34
19	34
20	34
1	35
2	35
3	35
4	35
5	35
6	35
7	35
8	35
9	35
10	35
11	35
12	35
13	35
14	35
15	35
16	35
17	35
18	35
19	35
20	35
1	36
2	36
3	36
4	36
5	36
6	36
7	36
8	36
9	36
10	36
11	36
12	36
13	36
14	36
15	36
16	36
17	36
18	36
19	36
20	36
1	37
2	37
3	37
4	37
5	37
6	37
7	37
8	37
9	37
10	37
11	37
12	37
13	37
14	37
15	37
16	37
17	37
18	37
19	37
20	37
1	38
2	38
3	38
4	38
5	38
6	38
7	38
8	38
9	38
10	38
11	38
12	38
13	38
14	38
15	38
16	38
17	38
18	38
19	38
20	38
1	39
2	39
3	39
4	39
5	39
6	39
7	39
8	39
9	39
10	39
11	39
12	39
13	39
14	39
15	39
16	39
17	39
18	39
19	39
20	39
1	40
2	40
3	40
4	40
5	40
6	40
7	40
8	40
9	40
10	40
11	40
12	40
13	40
14	40
15	40
16	40
17	40
18	40
19	40
20	40
1	41
2	41
3	41
4	41
5	41
6	41
7	41
8	41
9	41
10	41
11	41
12	41
13	41
14	41
15	41
16	41
17	41
18	41
19	41
20	41
1	42
2	42
3	42
4	42
5	42
6	42
7	42
8	42
9	42
10	42
11	42
12	42
13	42
14	42
15	42
16	42
17	42
18	42
19	42
20	42
1	43
2	43
3	43
4	43
5	43
6	43
7	43
8	43
9	43
10	43
11	43
12	43
13	43
14	43
15	43
16	43
17	43
18	43
19	43
20	43
1	44
2	44
3	44
4	44
5	44
6	44
7	44
8	44
9	44
10	44
11	44
12	44
13	44
14	44
15	44
16	44
17	44
18	44
19	44
20	44
1	45
2	45
3	45
4	45
5	45
6	45
7	45
8	45
9	45
10	45
11	45
12	45
13	45
14	45
15	45
16	45
17	45
18	45
19	45
20	45
1	46
2	46
3	46
4	46
5	46
6	46
7	46
8	46
9	46
10	46
11	46
12	46
13	46
14	46
15	46
16	46
17	46
18	46
19	46
20	46
1	47
2	47
3	47
4	47
5	47
6	47
7	47
8	47
9	47
10	47
11	47
12	47
13	47
14	47
15	47
16	47
17	47
18	47
19	47
20	47
1	48
2	48
3	48
4	48
5	48
6	48
7	48
8	48
9	48
10	48
11	48
12	48
13	48
14	48
15	48
16	48
17	48
18	48
19	48
20	48
1	49
2	49
3	49
4	49
5	49
6	49
7	49
8	49
9	49
10	49
11	49
12	49
13	49
14	49
15	49
16	49
17	49
18	49
19	49
20	49
1	50
2	50
3	50
4	50
5	50
6	50
7	50
8	50
9	50
10	50
11	50
12	50
13	50
14	50
15	50
16	50
17	50
18	50
19	50
20	50
1	51
2	51
3	51
4	51
5	51
6	51
7	51
8	51
9	51
10	51
11	51
12	51
13	51
14	51
15	51
16	51
17	51
18	51
19	51
20	51
1	52
2	52
3	52
4	52
5	52
6	52
7	52
8	52
9	52
10	52
11	52
12	52
13	52
14	52
15	52
16	52
17	52
18	52
19	52
20	52
1	53
2	53
3	53
4	53
5	53
6	53
7	53
8	53
9	53
10	53
11	53
12	53
13	53
14	53
15	53
16	53
17	53
18	53
19	53
20	53
1	54
2	54
3	54
4	54
5	54
6	54
7	54
8	54
9	54
10	54
11	54
12	54
13	54
14	54
15	54
16	54
17	54
18	54
19	54
20	54
1	55
2	55
3	55
4	55
5	55
6	55
7	55
8	55
9	55
10	55
11	55
12	55
13	55
14	55
15	55
16	55
17	55
18	55
19	55
20	55
1	56
2	56
3	56
4	56
5	56
6	56
7	56
8	56
9	56
10	56
11	56
12	56
13	56
14	56
15	56
16	56
17	56
18	56
19	56
20	56
1	57
2	57
3	57
4	57
5	57
6	57
7	57
8	57
9	57
10	57
11	57
12	57
13	57
14	57
15	57
16	57
17	57
18	57
19	57
20	57
1	58
2	58
3	58
4	58
5	58
6	58
7	58
8	58
9	58
10	58
11	58
12	58
13	58
14	58
15	58
16	58
17	58
18	58
19	58
20	58
1	59
2	59
3	59
4	59
5	59
6	59
7	59
8	59
9	59
10	59
11	59
12	59
13	59
14	59
15	59
16	59
17	59
18	59
19	59
20	59
1	60
2	60
3	60
4	60
5	60
6	60
7	60
8	60
9	60
10	60
11	60
12	60
13	60
14	60
15	60
16	60
17	60
18	60
19	60
20	60
1	61
2	61
3	61
4	61
5	61
6	61
7	61
8	61
9	61
10	61
11	61
12	61
13	61
14	61
15	61
16	61
17	61
18	61
19	61
20	61
1	62
2	62
3	62
4	62
5	62
6	62
7	62
8	62
9	62
10	62
11	62
12	62
13	62
14	62
15	62
16	62
17	62
18	62
19	62
20	62
1	63
2	63
3	63
4	63
5	63
6	63
7	63
8	63
9	63
10	63
11	63
12	63
13	63
14	63
15	63
16	63
17	63
18	63
19	63
20	63
1	64
2	64
3	64
4	64
5	64
6	64
7	64
8	64
9	64
10	64
11	64
12	64
13	64
14	64
15	64
16	64
17	64
18	64
19	64
20	64
1	65
2	65
3	65
4	65
5	65
6	65
7	65
8	65
9	65
10	65
11	65
12	65
13	65
14	65
15	65
16	65
17	65
18	65
19	65
20	65
1	66
2	66
3	66
4	66
5	66
6	66
7	66
8	66
9	66
10	66
11	66
12	66
13	66
14	66
15	66
16	66
17	66
18	66
19	66
20	66
1	67
2	67
3	67
4	67
5	67
6	67
7	67
8	67
9	67
10	67
11	67
12	67
13	67
14	67
15	67
16	67
17	67
18	67
19	67
20	67
1	68
2	68
3	68
4	68
5	68
6	68
7	68
8	68
9	68
10	68
11	68
12	68
13	68
14	68
15	68
16	68
17	68
18	68
19	68
20	68
1	69
2	69
3	69
4	69
5	69
6	69
7	69
8	69
9	69
10	69
11	69
12	69
13	69
14	69
15	69
16	69
17	69
18	69
19	69
20	69
1	70
2	70
3	70
4	70
5	70
6	70
7	70
8	70
9	70
10	70
11	70
12	70
13	70
14	70
15	70
16	70
17	70
18	70
19	70
20	70
1	71
2	71
3	71
4	71
5	71
6	71
7	71
8	71
9	71
10	71
11	71
12	71
13	71
14	71
15	71
16	71
17	71
18	71
19	71
20	71
1	72
2	72
3	72
4	72
5	72
6	72
7	72
8	72
9	72
10	72
11	72
12	72
13	72
14	72
15	72
16	72
17	72
18	72
19	72
20	72
1	73
2	73
3	73
4	73
5	73
6	73
7	73
8	73
9	73
10	73
11	73
12	73
13	73
14	73
15	73
16	73
17	73
18	73
19	73
20	73
1	74
2	74
3	74
4	74
5	74
6	74
7	74
8	74
9	74
10	74
11	74
12	74
13	74
14	74
15	74
16	74
17	74
18	74
19	74
20	74
1	75
2	75
3	75
4	75
5	75
6	75
7	75
8	75
9	75
10	75
11	75
12	75
13	75
14	75
15	75
16	75
17	75
18	75
19	75
20	75
1	76
2	76
3	76
4	76
5	76
6	76
7	76
8	76
9	76
10	76
11	76
12	76
13	76
14	76
15	76
16	76
17	76
18	76
19	76
20	76
1	77
2	77
3	77
4	77
5	77
6	77
7	77
8	77
9	77
10	77
11	77
12	77
13	77
14	77
15	77
16	77
17	77
18	77
19	77
20	77
1	78
2	78
3	78
4	78
5	78
6	78
7	78
8	78
9	78
10	78
11	78
12	78
13	78
14	78
15	78
16	78
17	78
18	78
19	78
20	78
1	79
2	79
3	79
4	79
5	79
6	79
7	79
8	79
9	79
10	79
11	79
12	79
13	79
14	79
15	79
16	79
17	79
18	79
19	79
20	79
1	80
2	80
3	80
4	80
5	80
6	80
7	80
8	80
9	80
10	80
11	80
12	80
13	80
14	80
15	80
16	80
17	80
18	80
19	80
20	80


grd40x40
1	1
2	1
3	1
4	1
5	1
6	1
7	1
8	1
9	1
10	1
11	1
12	1
13	1
14	1
15	1
16	1
17	1
18	1
19	1
20	1
21	1
22	1
23	1
24	1
25	1
26	1
27	1
28	1
29	1
30	1
31	1
32	1
33	1
34	1
35	1
36	1
37	1
38	1
39	1
40	1
1	2
2	2
3	2
4	2
5	2
6	2
7	2
8	2
9	2
10	2
11	2
12	2
13	2
14	2
15	2
16	2
17	2
18	2
19	2
20	2
21	2
22	2
23	2
24	2
25	2
26	2
27	2
28	2
29	2
30	2
31	2
32	2
33	2
34	2
35	2
36	2
37	2
38	2
39	2
40	2
1	3
2	3
3	3
4	3
5	3
6	3
7	3
8	3
9	3
10	3
11	3
12	3
13	3
14	3
15	3
16	3
17	3
18	3
19	3
20	3
21	3
22	3
23	3
24	3
25	3
26	3
27	3
28	3
29	3
30	3
31	3
32	3
33	3
34	3
35	3
36	3
37	3
38	3
39	3
40	3
1	4
2	4
3	4
4	4
5	4
6	4
7	4
8	4
9	4
10	4
11	4
12	4
13	4
14	4
15	4
16	4
17	4
18	4
19	4
20	4
21	4
22	4
23	4
24	4
25	4
26	4
27	4
28	4
29	4
30	4
31	4
32	4
33	4
34	4
35	4
36	4
37	4
38	4
39	4
40	4
1	5
2	5
3	5
4	5
5	5
6	5
7	5
8	5
9	5
10	5
11	5
12	5
13	5
14	5
15	5
16	5
17	5
18	5
19	5
20	5
21	5
22	5
23	5
24	5
25	5
26	5
27	5
28	5
29	5
30	5
31	5
32	5
33	5
34	5
35	5
36	5
37	5
38	5
39	5
40	5
1	6
2	6
3	6
4	6
5	6
6	6
7	6
8	6
9	6
10	6
11	6
12	6
13	6
14	6
15	6
16	6
17	6
18	6
19	6
20	6
21	6
22	6
23	6
24	6
25	6
26	6
27	6
28	6
29	6
30	6
31	6
32	6
33	6
34	6
35	6
36	6
37	6
38	6
39	6
40	6
1	7
2	7
3	7
4	7
5	7
6	7
7	7
8	7
9	7
10	7
11	7
12	7
13	7
14	7
15	7
16	7
17	7
18	7
19	7
20	7
21	7
22	7
23	7
24	7
25	7
26	7
27	7
28	7
29	7
30	7
31	7
32	7
33	7
34	7
35	7
36	7
37	7
38	7
39	7
40	7
1	8
2	8
3	8
4	8
5	8
6	8
7	8
8	8
9	8
10	8
11	8
12	8
13	8
14	8
15	8
16	8
17	8
18	8
19	8
20	8
21	8
22	8
23	8
24	8
25	8
26	8
27	8
28	8
29	8
30	8
31	8
32	8
33	8
34	8
35	8
36	8
37	8
38	8
39	8
40	8
1	9
2	9
3	9
4	9
5	9
6	9
7	9
8	9
9	9
10	9
11	9
12	9
13	9
14	9
15	9
16	9
17	9
18	9
19	9
20	9
21	9
22	9
23	9
24	9
25	9
26	9
27	9
28	9
29	9
30	9
31	9
32	9
33	9
34	9
35	9
36	9
37	9
38	9
39	9
40	9
1	10
2	10
3	10
4	10
5	10
6	10
7	10
8	10
9	10
10	10
11	10
12	10
13	10
14	10
15	10
16	10
17	10
18	10
19	10
20	10
21	10
22	10
23	10
24	10
25	10
26	10
27	10
28	10
29	10
30	10
31	10
32	10
33	10
34	10
35	10
36	10
37	10
38	10
39	10
40	10
1	11
2	11
3	11
4	11
5	11
6	11
7	11
8	11
9	11
10	11
11	11
12	11
13	11
14	11
15	11
16	11
17	11
18	11
19	11
20	11
21	11
22	11
23	11
24	11
25	11
26	11
27	11
28	11
29	11
30	11
31	11
32	11
33	11
34	11
35	11
36	11
37	11
38	11
39	11
40	11
1	12
2	12
3	12
4	12
5	12
6	12
7	12
8	12
9	12
10	12
11	12
12	12
13	12
14	12
15	12
16	12
17	12
18	12
19	12
20	12
21	12
22	12
23	12
24	12
25	12
26	12
27	12
28	12
29	12
30	12
31	12
32	12
33	12
34	12
35	12
36	12
37	12
38	12
39	12
40	12
1	13
2	13
3	13
4	13
5	13
6	13
7	13
8	13
9	13
10	13
11	13
12	13
13	13
14	13
15	13
16	13
17	13
18	13
19	13
20	13
21	13
22	13
23	13
24	13
25	13
26	13
27	13
28	13
29	13
30	13
31	13
32	13
33	13
34	13
35	13
36	13
37	13
38	13
39	13
40	13
1	14
2	14
3	14
4	14
5	14
6	14
7	14
8	14
9	14
10	14
11	14
12	14
13	14
14	14
15	14
16	14
17	14
18	14
19	14
20	14
21	14
22	14
23	14
24	14
25	14
26	14
27	14
28	14
29	14
30	14
31	14
32	14
33	14
34	14
35	14
36	14
37	14
38	14
39	14
40	14
1	15
2	15
3	15
4	15
5	15
6	15
7	15
8	15
9	15
10	15
11	15
12	15
13	15
14	15
15	15
16	15
17	15
18	15
19	15
20	15
21	15
22	15
23	15
24	15
25	15
26	15
27	15
28	15
29	15
30	15
31	15
32	15
33	15
34	15
35	15
36	15
37	15
38	15
39	15
40	15
1	16
2	16
3	16
4	16
5	16
6	16
7	16
8	16
9	16
10	16
11	16
12	16
13	16
14	16
15	16
16	16
17	16
18	16
19	16
20	16
21	16
22	16
23	16
24	16
25	16
26	16
27	16
28	16
29	16
30	16
31	16
32	16
33	16
34	16
35	16
36	16
37	16
38	16
39	16
40	16
1	17
2	17
3	17
4	17
5	17
6	17
7	17
8	17
9	17
10	17
11	17
12	17
13	17
14	17
15	17
16	17
17	17
18	17
19	17
20	17
21	17
22	17
23	17
24	17
25	17
26	17
27	17
28	17
29	17
30	17
31	17
32	17
33	17
34	17
35	17
36	17
37	17
38	17
39	17
40	17
1	18
2	18
3	18
4	18
5	18
6	18
7	18
8	18
9	18
10	18
11	18
12	18
13	18
14	18
15	18
16	18
17	18
18	18
19	18
20	18
21	18
22	18
23	18
24	18
25	18
26	18
27	18
28	18
29	18
30	18
31	18
32	18
33	18
34	18
35	18
36	18
37	18
38	18
39	18
40	18
1	19
2	19
3	19
4	19
5	19
6	19
7	19
8	19
9	19
10	19
11	19
12	19
13	19
14	19
15	19
16	19
17	19
18	19
19	19
20	19
21	19
22	19
23	19
24	19
25	19
26	19
27	19
28	19
29	19
30	19
31	19
32	19
33	19
34	19
35	19
36	19
37	19
38	19
39	19
40	19
1	20
2	20
3	20
4	20
5	20
6	20
7	20
8	20
9	20
10	20
11	20
12	20
13	20
14	20
15	20
16	20
17	20
18	20
19	20
20	20
21	20
22	20
23	20
24	20
25	20
26	20
27	20
28	20
29	20
30	20
31	20
32	20
33	20
34	20
35	20
36	20
37	20
38	20
39	20
40	20
1	21
2	21
3	21
4	21
5	21
6	21
7	21
8	21
9	21
10	21
11	21
12	21
13	21
14	21
15	21
16	21
17	21
18	21
19	21
20	21
21	21
22	21
23	21
24	21
25	21
26	21
27	21
28	21
29	21
30	21
31	21
32	21
33	21
34	21
35	21
36	21
37	21
38	21
39	21
40	21
1	22
2	22
3	22
4	22
5	22
6	22
7	22
8	22
9	22
10	22
11	22
12	22
13	22
14	22
15	22
16	22
17	22
18	22
19	22
20	22
21	22
22	22
23	22
24	22
25	22
26	22
27	22
28	22
29	22
30	22
31	22
32	22
33	22
34	22
35	22
36	22
37	22
38	22
39	22
40	22
1	23
2	23
3	23
4	23
5	23
6	23
7	23
8	23
9	23
10	23
11	23
12	23
13	23
14	23
15	23
16	23
17	23
18	23
19	23
20	23
21	23
22	23
23	23
24	23
25	23
26	23
27	23
28	23
29	23
30	23
31	23
32	23
33	23
34	23
35	23
36	23
37	23
38	23
39	23
40	23
1	24
2	24
3	24
4	24
5	24
6	24
7	24
8	24
9	24
10	24
11	24
12	24
13	24
14	24
15	24
16	24
17	24
18	24
19	24
20	24
21	24
22	24
23	24
24	24
25	24
26	24
27	24
28	24
29	24
30	24
31	24
32	24
33	24
34	24
35	24
36	24
37	24
38	24
39	24
40	24
1	25
2	25
3	25
4	25
5	25
6	25
7	25
8	25
9	25
10	25
11	25
12	25
13	25
14	25
15	25
16	25
17	25
18	25
19	25
20	25
21	25
22	25
23	25
24	25
25	25
26	25
27	25
28	25
29	25
30	25
31	25
32	25
33	25
34	25
35	25
36	25
37	25
38	25
39	25
40	25
1	26
2	26
3	26
4	26
5	26
6	26
7	26
8	26
9	26
10	26
11	26
12	26
13	26
14	26
15	26
16	26
17	26
18	26
19	26
20	26
21	26
22	26
23	26
24	26
25	26
26	26
27	26
28	26
29	26
30	26
31	26
32	26
33	26
34	26
35	26
36	26
37	26
38	26
39	26
40	26
1	27
2	27
3	27
4	27
5	27
6	27
7	27
8	27
9	27
10	27
11	27
12	27
13	27
14	27
15	27
16	27
17	27
18	27
19	27
20	27
21	27
22	27
23	27
24	27
25	27
26	27
27	27
28	27
29	27
30	27
31	27
32	27
33	27
34	27
35	27
36	27
37	27
38	27
39	27
40	27
1	28
2	28
3	28
4	28
5	28
6	28
7	28
8	28
9	28
10	28
11	28
12	28
13	28
14	28
15	28
16	28
17	28
18	28
19	28
20	28
21	28
22	28
23	28
24	28
25	28
26	28
27	28
28	28
29	28
30	28
31	28
32	28
33	28
34	28
35	28
36	28
37	28
38	28
39	28
40	28
1	29
2	29
3	29
4	29
5	29
6	29
7	29
8	29
9	29
10	29
11	29
12	29
13	29
14	29
15	29
16	29
17	29
18	29
19	29
20	29
21	29
22	29
23	29
24	29
25	29
26	29
27	29
28	29
29	29
30	29
31	29
32	29
33	29
34	29
35	29
36	29
37	29
38	29
39	29
40	29
1	30
2	30
3	30
4	30
5	30
6	30
7	30
8	30
9	30
10	30
11	30
12	30
13	30
14	30
15	30
16	30
17	30
18	30
19	30
20	30
21	30
22	30
23	30
24	30
25	30
26	30
27	30
28	30
29	30
30	30
31	30
32	30
33	30
34	30
35	30
36	30
37	30
38	30
39	30
40	30
1	31
2	31
3	31
4	31
5	31
6	31
7	31
8	31
9	31
10	31
11	31
12	31
13	31
14	31
15	31
16	31
17	31
18	31
19	31
20	31
21	31
22	31
23	31
24	31
25	31
26	31
27	31
28	31
29	31
30	31
31	31
32	31
33	31
34	31
35	31
36	31
37	31
38	31
39	31
40	31
1	32
2	32
3	32
4	32
5	32
6	32
7	32
8	32
9	32
10	32
11	32
12	32
13	32
14	32
15	32
16	32
17	32
18	32
19	32
20	32
21	32
22	32
23	32
24	32
25	32
26	32
27	32
28	32
29	32
30	32
31	32
32	32
33	32
34	32
35	32
36	32
37	32
38	32
39	32
40	32
1	33
2	33
3	33
4	33
5	33
6	33
7	33
8	33
9	33
10	33
11	33
12	33
13	33
14	33
15	33
16	33
17	33
18	33
19	33
20	33
21	33
22	33
23	33
24	33
25	33
26	33
27	33
28	33
29	33
30	33
31	33
32	33
33	33
34	33
35	33
36	33
37	33
38	33
39	33
40	33
1	34
2	34
3	34
4	34
5	34
6	34
7	34
8	34
9	34
10	34
11	34
12	34
13	34
14	34
15	34
16	34
17	34
18	34
19	34
20	34
21	34
22	34
23	34
24	34
25	34
26	34
27	34
28	34
29	34
30	34
31	34
32	34
33	34
34	34
35	34
36	34
37	34
38	34
39	34
40	34
1	35
2	35
3	35
4	35
5	35
6	35
7	35
8	35
9	35
10	35
11	35
12	35
13	35
14	35
15	35
16	35
17	35
18	35
19	35
20	35
21	35
22	35
23	35
24	35
25	35
26	35
27	35
28	35
29	35
30	35
31	35
32	35
33	35
34	35
35	35
36	35
37	35
38	35
39	35
40	35
1	36
2	36
3	36
4	36
5	36
6	36
7	36
8	36
9	36
10	36
11	36
12	36
13	36
14	36
15	36
16	36
17	36
18	36
19	36
20	36
21	36
22	36
23	36
24	36
25	36
26	36
27	36
28	36
29	36
30	36
31	36
32	36
33	36
34	36
35	36
36	36
37	36
38	36
39	36
40	36
1	37
2	37
3	37
4	37
5	37
6	37
7	37
8	37
9	37
10	37
11	37
12	37
13	37
14	37
15	37
16	37
17	37
18	37
19	37
20	37
21	37
22	37
23	37
24	37
25	37
26	37
27	37
28	37
29	37
30	37
31	37
32	37
33	37
34	37
35	37
36	37
37	37
38	37
39	37
40	37
1	38
2	38
3	38
4	38
5	38
6	38
7	38
8	38
9	38
10	38
11	38
12	38
13	38
14	38
15	38
16	38
17	38
18	38
19	38
20	38
21	38
22	38
23	38
24	38
25	38
26	38
27	38
28	38
29	38
30	38
31	38
32	38
33	38
34	38
35	38
36	38
37	38
38	38
39	38
40	38
1	39
2	39
3	39
4	39
5	39
6	39
7	39
8	39
9	39
10	39
11	39
12	39
13	39
14	39
15	39
16	39
17	39
18	39
19	39
20	39
21	39
22	39
23	39
24	39
25	39
26	39
27	39
28	39
29	39
30	39
31	39
32	39
33	39
34	39
35	39
36	39
37	39
38	39
39	39
40	39
1	40
2	40
3	40
4	40
5	40
6	40
7	40
8	40
9	40
10	40
11	40
12	40
13	40
14	40
15	40
16	40
17	40
18	40
19	40
20	40
21	40
22	40
23	40
24	40
25	40
26	40
27	40
28	40
29	40
30	40
31	40
32	40
33	40
34	40
35	40
36	40
37	40
38	40
39	40
40	40


stream0
1	1
2	1
3	1
4	1
5	1
6	1
7	1
8	1
9	1
10	1
11	1
12	1
13	1
14	1
15	1
16	1
17	1
18	1
19	1
20	1
21	1
22	1
23	1
24	1
25	1
26	1
27	1
28	1
29	1
30	1
31	1
32	1
33	1
34	1
35	1
36	1
37	1
38	1
39	1
40	1
41	1
42	1
43	1
44	1
45	1
46	1
47	1
48	1
49	1
50	1
51	1
52	1
53	1
54	1
55	1
56	1
57	1
58	1
59	1
60	1
61	1
62	1
63	1
64	1
65	1
66	1
67	1
68	1
69	1
70	1
71	1
72	1
73	1
74	1
75	1
76	1
77	1
78	1
79	1
80	1
81	1
82	1
83	1
84	1
85	1
86	1
87	1
88	1
89	1
90	1
91	1
92	1
93	1
94	1
95	1
96	1
97	1
98	1
99	1
100	1
101	1
102	1
103	1
104	1
105	1
106	1
107	1
108	1
109	1
110	1
111	1
112	1
113	1
114	1
115	1
116	1
117	1
118	1
119	1
120	1
121	1
122	1
123	1
124	1
125	1
126	1
127	1
128	1
129	1
130	1
131	1
132	1
133	1
134	1
135	1
136	1
137	1
138	1
139	1
140	1
141	1
142	1
143	1
144	1
145	1
146	1
147	1
148	1
149	1
150	1
151	1
152	1
153	1
154	1
155	1
156	1
157	1
158	1
159	1
160	1
161	1
162	1
163	1
164	1
165	1
166	1
167	1
168	1
169	1
170	1
171	1
172	1
173	1
174	1
175	1
176	1
177	1
178	1
179	1
180	1
181	1
182	1
183	1
184	1
185	1
186	1
187	1
188	1
189	1
190	1
191	1
192	1
193	1
194	1
195	1
196	1
197	1
198	1
199	1
200	1
201	1
202	1
203	1
204	1
205	1
206	1
207	1
208	1
209	1
210	1
211	1
212	1
213	1
214	1
215	1
216	1
217	1
218	1
219	1
220	1
221	1
222	1
223	1
224	1
225	1
226	1
227	1
228	1
229	1
230	1
231	1
232	1
233	1
234	1
235	1
236	1
237	1
238	1
239	1
240	1
241	1
242	1
243	1
244	1
245	1
246	1
247	1
248	1
249	1
250	1
251	1
252	1
253	1
254	1
255	1
256	1
257	1
258	1
259	1
260	1
261	1
262	1
263	1
264	1
265	1
266	1
267	1
268	1
269	1
270	1
271	1
272	1
273	1
274	1
275	1
276	1
277	1
278	1
279	1
280	1
281	1
282	1
283	1
284	1
285	1
286	1
287	1
288	1
289	1
290	1
291	1
292	1
293	1
294	1
295	1
296	1
297	1
298	1
299	1
300	1
301	1
302	1
303	1
304	1
305	1
306	1
307	1
308	1
309	1
310	1
311	1
312	1
313	1
314	1
315	1
316	1
317	1
318	1
319	1
320	1
321	1
322	1
323	1
324	1
325	1
326	1
327	1
328	1
329	1
330	1
331	1
332	1
333	1
334	1
335	1
336	1
337	1
338	1
339	1
340	1
341	1
342	1
343	1
344	1
345	1
346	1
347	1
348	1
349	1
350	1
351	1
352	1
353	1
354	1
355	1
356	1
357	1
358	1
359	1
360	1
361	1
362	1
363	1
364	1
365	1
366	1
367	1
368	1
369	1
370	1
371	1
372	1
373	1
374	1
375	1
376	1
377	1
378	1
379	1
380	1
381	1
382	1
383	1
384	1
385	1
386	1
387	1
388	1
389	1
390	1
391	1
392	1
393	1
394	1
395	1
396	1
397	1
398	1
399	1
400	1
401	1
402	1
403	1
404	1
405	1
406	1
407	1
408	1
409	1
410	1
411	1
412	1
413	1
414	1
415	1
416	1
417	1
418	1
419	1
420	1
421	1
422	1
423	1
424	1
425	1
426	1
427	1
428	1
429	1
430	1
431	1
432	1
433	1
434	1
435	1
436	1
437	1
438	1
439	1
440	1
441	1
442	1
443	1
444	1
445	1
446	1
447	1
448	1
449	1
450	1
451	1
452	1
453	1
454	1
455	1
456	1
457	1
458	1
459	1
460	1
461	1
462	1
463	1
464	1
465	1
466	1
467	1
468	1
469	1
470	1
471	1
472	1
473	1
474	1
475	1
476	1
477	1
478	1
479	1
480	1
481	1
482	1
483	1
484	1
485	1
486	1
487	1
488	1
489	1
490	1
491	1
492	1
493	1
494	1
495	1
496	1
497	1
498	1
499	1
500	1
501	1
502	1
503	1
504	1
505	1
506	1
507	1
508	1
509	1
510	1
511	1
512	1
513	1
514	1
515	1
516	1
517	1
518	1
519	1
520	1
521	1
522	1
523	1
524	1
525	1
526	1
527	1
528	1
529	1
530	1
531	1
532	1
533	1
534	1
535	1
536	1
537	1
538	1
539	1
540	1
541	1
542	1
543	1
544	1
545	1
546	1
547	1
548	1
549	1
550	1
551	1
552	1
553	1
554	1
555	1
556	1
557	1
558	1
559	1
560	1
561	1
562	1
563	1
564	1
565	1
566	1
567	1
568	1
569	1
570	1
571	1
572	1
573	1
574	1
575	1
576	1
577	1
578	1
579	1
580	1
581	1
582	1
583	1
584	1
585	1
586	1
587	1
588	1
589	1
590	1
591	1
592	1
593	1
594	1
595	1
596	1
597	1
598	1
599	1
600	1
601	1
602	1
603	1
604	1
605	1
606	1
607	1
608	1
609	1
610	1
611	1
612	1
613	1
614	1
615	1
616	1
617	1
618	1
619	1
620	1
621	1
622	1
623	1
624	1
625	1
626	1
627	1
628	1
629	1
630	1
631	1
632	1
633	1
634	1
635	1
636	1
637	1
638	1
639	1
640	1
641	1
642	1
643	1
644	1
645	1
646	1
647	1
648	1
649	1
650	1
651	1
652	1
653	1
654	1
655	1
656	1
657	1
658	1
659	1
660	1
661	1
662	1
663	1
664	1
665	1
666	1
667	1
668	1
669	1
670	1
671	1
672	1
673	1
674	1
675	1
676	1
677	1
678	1
679	1
680	1
681	1
682	1
683	1
684	1
685	1
686	1
687	1
688	1
689	1
690	1
691	1
692	1
693	1
694	1
695	1
696	1
697	1
698	1
699	1
700	1
701	1
702	1
703	1
704	1
705	1
706	1
707	1
708	1
709	1
710	1
711	1
712	1
713	1
714	1
715	1
716	1
717	1
718	1
719	1
720	1
721	1
722	1
723	1
724	1
725	1
726	1
727	1
728	1
729	1
730	1
731	1
732	1
733	1
734	1
735	1
736	1
737	1
738	1
739	1
740	1
741	1
742	1
743	1
744	1
745	1
746	1
747	1
748	1
749	1
750	1
751	1
752	1
753	1
754	1
755	1
756	1
757	1
758	1
759	1
760	1
761	1
762	1
763	1
764	1
765	1
766	1
767	1
768	1
769	1
770	1
771	1
772	1
773	1
774	1
775	1
776	1
777	1
778	1
779	1
780	1
781	1
782	1
783	1
784	1
785	1
786	1
787	1
788	1
789	1
790	1
791	1
792	1
793	1
794	1
795	1
796	1
797	1
798	1
799	1
800	1
801	1
802	1
803	1
804	1
805	1
806	1
807	1
808	1
809	1
810	1
811	1
812	1
813	1
814	1
815	1
816	1
817	1
818	1
819	1
820	1
821	1
822	1
823	1
824	1
825	1
826	1
827	1
828	1
829	1
830	1
831	1
832	1
833	1
834	1
835	1
836	1
837	1
838	1
839	1
840	1
841	1
842	1
843	1
844	1
845	1
846	1
847	1
848	1
849	1
850	1
851	1
852	1
853	1
854	1
855	1
856	1
857	1
858	1
859	1
860	1
861	1
862	1
863	1
864	1
865	1
866	1
867	1
868	1
869	1
870	1
871	1
872	1
873	1
874	1
875	1
876	1
877	1
878	1
879	1
880	1
881	1
882	1
883	1
884	1
885	1
886	1
887	1
888	1
889	1
890	1
891	1
892	1
893	1
894	1
895	1
896	1
897	1
898	1
899	1
900	1
901	1
902	1
903	1
904	1
905	1
906	1
907	1
908	1
909	1
910	1
911	1
912	1
913	1
914	1
915	1
916	1
917	1
918	1
919	1
920	1
921	1
922	1
923	1
924	1
925	1
926	1
927	1
928	1
929	1
930	1
931	1
932	1
933	1
934	1
935	1
936	1
937	1
938	1
939	1
940	1
941	1
942	1
943	1
944	1
945	1
946	1
947	1
948	1
949	1
950	1
951	1
952	1
953	1
954	1
955	1
956	1
957	1
958	1
959	1
960	1
961	1
962	1
963	1
964	1
965	1
966	1
967	1
968	1
969	1
970	1
971	1
972	1
973	1
974	1
975	1
976	1
977	1
978	1
979	1
980	1
981	1
982	1
983	1
984	1
985	1
986	1
987	1
988	1
989	1
990	1
991	1
992	1
993	1
994	1
995	1
996	1
997	1
998	1
999	1
1000	1
1001	1
1002	1
1003	1
1004	1
1005	1
1006	1
1007	1
1008	1
1009	1
1010	1
1011	1
1012	1
1013	1
1014	1
1015	1
1016	1
1017	1
1018	1
1019	1
1020	1
1021	1
1022	1
1023	1
1024	1
1025	1
1026	1
1027	1
1028	1
1029	1
1030	1
1031	1
1032	1
1033	1
1034	1
1035	1
1036	1
1037	1
1038	1
1039	1
1040	1
1041	1
1042	1
1043	1
1044	1
1045	1
1046	1
1047	1
1048	1
1049	1
1050	1
1051	1
1052	1
1053	1
1054	1
1055	1
1056	1
1057	1
1058	1
1059	1
1060	1
1061	1
1062	1
1063	1
1064	1
1065	1
1066	1
1067	1
1068	1
1069	1
1070	1
1071	1
1072	1
1073	1
1074	1
1075	1
1076	1
1077	1
1078	1
1079	1
1080	1
1081	1
1082	1
1083	1
1084	1
1085	1
1086	1
1087	1
1088	1
1089	1
1090	1
1091	1
1092	1
1093	1
1094	1
1095	1
1096	1
1097	1
1098	1
1099	1
1100	1
1101	1
1102	1
1103	1
1104	1
1105	1
1106	1
1107	1
1108	1
1109	1
1110	1
1111	1
1112	1
1113	1
1114	1
1115	1
1116	1
1117	1
1118	1
1119	1
1120	1
1121	1
1122	1
1123	1
1124	1
1125	1
1126	1
1127	1
1128	1
1129	1
1130	1
1131	1
1132	1
1133	1
1134	1
1135	1
1136	1
1137	1
1138	1
1139	1
1140	1
1141	1
1142	1
1143	1
1144	1
1145	1
1146	1
1147	1
1148	1
1149	1
1150	1
1151	1
1152	1
1153	1
1154	1
1155	1
1156	1
1157	1
1158	1
1159	1
1160	1
1161	1
1162	1
1163	1
1164	1
1165	1
1166	1
1167	1
1168	1
1169	1
1170	1
1171	1
1172	1
1173	1
1174	1
1175	1
1176	1
1177	1
1178	1
1179	1
1180	1
1181	1
1182	1
1183	1
1184	1
1185	1
1186	1
1187	1
1188	1
1189	1
1190	1
1191	1
1192	1
1193	1
1194	1
1195	1
1196	1
1197	1
1198	1
1199	1
1200	1
1201	1
1202	1
1203	1
1204	1
1205	1
1206	1
1207	1
1208	1
1209	1
1210	1
1211	1
1212	1
1213	1
1214	1
1215	1
1216	1
1217	1
1218	1
1219	1
1220	1
1221	1
1222	1
1223	1
1224	1
1225	1
1226	1
1227	1
1228	1
1229	1
1230	1
1231	1
1232	1
1233	1
1234	1
1235	1
1236	1
1237	1
1238	1
1239	1
1240	1
1241	1
1242	1
1243	1
1244	1
1245	1
1246	1
1247	1
1248	1
1249	1
1250	1
1251	1
1252	1
1253	1
1254	1
1255	1
1256	1
1257	1
1258	1
1259	1
1260	1
1261	1
1262	1
1263	1
1264	1
1265	1
1266	1
1267	1
1268	1
1269	1
1270	1
1271	1
1272	1
1273	1
1274	1
1275	1
1276	1
1277	1
1278	1
1279	1
1280	1
1281	1
1282	1
1283	1
1284	1
1285	1
1286	1
1287	1
1288	1
1289	1
1290	1
1291	1
1292	1
1293	1
1294	1
1295	1
1296	1
1297	1
1298	1
1299	1
1300	1
1301	1
1302	1
1303	1
1304	1
1305	1
1306	1
1307	1
1308	1
1309	1
1310	1
1311	1
1312	1
1313	1
1314	1
1315	1
1316	1
1317	1
1318	1
1319	1
1320	1
1321	1
1322	1
1323	1
1324	1
1325	1
1326	1
1327	1
1328	1
1329	1
1330	1
1331	1
1332	1
1333	1
1334	1
1335	1
1336	1
1337	1
1338	1
1339	1
1340	1
1341	1
1342	1
1343	1
1344	1
1345	1
1346	1
1347	1
1348	1
1349	1
1350	1
1351	1
1352	1
1353	1
1354	1
1355	1
1356	1
1357	1
1358	1
1359	1
1360	1
1361	1
1362	1
1363	1
1364	1
1365	1
1366	1
1367	1
1368	1
1369	1
1370	1
1371	1
1372	1
1373	1
1374	1
1375	1
1376	1
1377	1
1378	1
1379	1
1380	1
1381	1
1382	1
1383	1
1384	1
1385	1
1386	1
1387	1
1388	1
1389	1
1390	1
1391	1
1392	1
1393	1
1394	1
1395	1
1396	1
1397	1
1398	1
1399	1
1400	1
1401	1
1402	1
1403	1
1404	1
1405	1
1406	1
1407	1
1408	1
1409	1
1410	1
1411	1
1412	1
1413	1
1414	1
1415	1
1416	1
1417	1
1418	1
1419	1
1420	1
1421	1
1422	1
1423	1
1424	1
1425	1
1426	1
1427	1
1428	1
1429	1
1430	1
1431	1
1432	1
1433	1
1434	1
1435	1
1436	1
1437	1
1438	1
1439	1
1440	1
1441	1
1442	1
1443	1
1444	1
1445	1
1446	1
1447	1
1448	1
1449	1
1450	1
1451	1
1452	1
1453	1
1454	1
1455	1
1456	1
1457	1
1458	1
1459	1
1460	1
1461	1
1462	1
1463	1
1464	1
1465	1
1466	1
1467	1
1468	1
1469	1
1470	1
1471	1
1472	1
1473	1
1474	1
1475	1
1476	1
1477	1
1478	1
1479	1
1480	1
1481	1
1482	1
1483	1
1484	1
1485	1
1486	1
1487	1
1488	1
1489	1
1490	1
1491	1
1492	1
1493	1
1494	1
1495	1
1496	1
1497	1
1498	1
1499	1
1500	1
1501	1
1502	1
1503	1
1504	1
1505	1
1506	1
1507	1
1508	1
1509	1
1510	1
1511	1
1512	1
1513	1
1514	1
1515	1
1516	1
1517	1
1518	1
1519	1
1520	1
1521	1
1522	1
1523	1
1524	1
1525	1
1526	1
1527	1
1528	1
1529	1
1530	1
1531	1
1532	1
1533	1
1534	1
1535	1
1536	1
1537	1
1538	1
1539	1
1540	1
1541	1
1542	1
1543	1
1544	1
1545	1
1546	1
1547	1
1548	1
1549	1
1550	1
1551	1
1552	1
1553	1
1554	1
1555	1
1556	1
1557	1
1558	1
1559	1
1560	1
1561	1
1562	1
1563	1
1564	1
1565	1
1566	1
1567	1
1568	1
1569	1
1570	1
1571	1
1572	1
1573	1
1574	1
1575	1
1576	1
1577	1
1578	1
1579	1
1580	1
1581	1
1582	1
1583	1
1584	1
1585	1
1586	1
1587	1
1588	1
1589	1
1590	1
1591	1
1592	1
1593	1
1594	1
1595	1
1596	1
1597	1
1598	1
1599	1
1600	1


stream10
60	1
61	1
62	1
63	1
64	1
65	1
66	1
67	1
68	1
69	1
70	1
71	1
72	1
73	1
74	1
75	1
76	1
77	1
78	1
79	1
80	1
81	1
82	1
83	1
84	1
85	1
86	1
87	1
88	1
89	1
90	1
91	1
92	1
93	1
94	1
95	1
96	1
97	1
98	1
99	1
100	1
101	1
102	1
103	1
104	1
105	1
106	1
107	1
108	1
109	1
110	1
111	1
112	1
113	1
114	1
115	1
116	1
117	1
118	1
119	1
120	1
121	1
122	1
123	1
124	1
125	1
126	1
127	1
128	1
129	1
130	1
131	1
132	1
133	1
134	1
135	1
136	1
137	1
138	1
139	1
140	1
100	2
100	3
100	4
100	5
100	6
100	7
100	8
100	9
100	10
100	11
100	12
100	13
100	14
100	15
100	16
100	17
100	18
100	19
100	20
100	21
100	22
100	23
100	24
100	25
100	26
100	27
100	28
100	29
100	30
100	31
100	32
100	33
100	34
100	35
100	36
100	37
100	38
100	39
100	40
100	41
100	42
100	43
100	44
100	45
100	46
100	47
100	48
100	49
100	50
100	51
100	52
100	53
100	54
100	55
100	56
100	57
100	58
100	59
100	60
100	61
100	62
100	63
100	64
100	65
100	66
100	67
100	68
100	69
100	70
100	71
100	72
100	73
100	74
100	75
100	76
100	77
100	78
100	79
20	80
21	80
22	80
23	80
24	80
25	80
26	80
27	80
28	80
29	80
30	80
31	80
32	80
33	80
34	80
35	80
36	80
37	80
38	80
39	80
40	80
41	80
42	80
43	80
44	80
45	80
46	80
47	80
48	80
49	80
50	80
51	80
52	80
53	80
54	80
55	80
56	80
57	80
58	80
59	80
60	80
61	80
62	80
63	80
64	80
65	80
66	80
67	80
68	80
69	80
70	80
71	80
72	80
73	80
74	80
75	80
76	80
77	80
78	80
79	80
80	80
81	80
82	80
83	80
84	80
85	80
86	80
87	80
88	80
89	80
90	80
91	80
92	80
93	80
94	80
95	80
96	80
97	80
98	80
99	80
100	80
100	81
100	82
100	83
100	84
100	85
100	86
100	87
100	88
100	89
100	90
100	91
100	92
100	93
100	94
100	95
100	96
100	97
100	98
100	99
100	100
100	101
100	102
100	103
100	104
100	105
100	106
100	107
100	108
100	109
100	110
100	111
100	112
100	113
100	114
100	115
100	116
100	117
100	118
100	119
100	120
100	121
100	122
100	123
100	124
100	125
100	126
100	127
100	128
100	129
100	130
100	131
100	132
100	133
100	134
100	135
100	136
100	137
100	138
100	139
100	140
100	141
100	142
100	143
100	144
100	145
100	146
100	147
100	148
100	149
100	150
100	151
100	152
100	153
100	154
100	155
100	156
100	157
100	158
100	159
100	160
101	160
102	160
103	160
104	160
105	160
106	160
107	160
108	160
109	160
110	160
111	160
112	160
113	160
114	160
115	160
116	160
117	160
118	160
119	160
120	160
121	160
122	160
123	160
124	160
125	160
126	160
127	160
128	160
129	160
130	160
131	160
132	160
133	160
134	160
135	160
136	160
137	160
138	160
139	160
140	160
141	160
142	160
143	160
144	160
145	160
146	160
147	160
148	160
149	160
150	160
151	160
152	160
153	160
154	160
155	160
156	160
157	160
158	160
159	160
160	160
161	160
162	160
163	160
164	160
165	160
166	160
167	160
168	160
169	160
170	160
171	160
172	160
173	160
174	160
175	160
176	160
177	160
178	160
179	160
180	160
100	161
100	162
100	163
100	164
100	165
100	166
100	167
100	168
100	169
100	170
100	171
100	172
100	173
100	174
100	175
100	176
100	177
100	178
100	179
100	180
100	181
100	182
100	183
100	184
100	185
100	186
100	187
100	188
100	189
100	190
100	191
100	192
100	193
100	194
100	195
100	196
100	197
100	198
100	199
100	200
100	201
100	202
100	203
100	204
100	205
100	206
100	207
100	208
100	209
100	210
100	211
100	212
100	213
100	214
100	215
100	216
100	217
100	218
100	219
100	220
100	221
100	222
100	223
100	224
100	225
100	226
100	227
100	228
100	229
100	230
100	231
100	232
100	233
100	234
100	235
100	236
100	237
100	238
100	239
20	240
21	240
22	240
23	240
24	240
25	240
26	240
27	240
28	240
29	240
30	240
31	240
32	240
33	240
34	240
35	240
36	240
37	240
38	240
39	240
40	240
41	240
42	240
43	240
44	240
45	240
46	240
47	240
48	240
49	240
50	240
51	240
52	240
53	240
54	240
55	240
56	240
57	240
58	240
59	240
60	240
61	240
62	240
63	240
64	240
65	240
66	240
67	240
68	240
69	240
70	240
71	240
72	240
73	240
74	240
75	240
76	240
77	240
78	240
79	240
80	240
81	240
82	240
83	240
84	240
85	240
86	240
87	240
88	240
89	240
90	240
91	240
92	240
93	240
94	240
95	240
96	240
97	240
98	240
99	240
100	240
100	241
100	242
100	243
100	244
100	245
100	246
100	247
100	248
100	249
100	250
100	251
100	252
100	253
100	254
100	255
100	256
100	257
100	258
100	259
100	260
100	261
100	262
100	263
100	264
100	265
100	266
100	267
100	268
100	269
100	270
100	271
100	272
100	273
100	274
100	275
100	276
100	277
100	278
100	279
100	280
100	281
100	282
100	283
100	284
100	285
100	286
100	287
100	288
100	289
100	290
100	291
100	292
100	293
100	294
100	295
100	296
100	297
100	298
100	299
100	300
100	301
100	302
100	303
100	304
100	305
100	306
100	307
100	308
100	309
100	310
100	311
100	312
100	313
100	314
100	315
100	316
100	317
100	318
100	319
100	320
101	320
102	320
103	320
104	320
105	320
106	320
107	320
108	320
109	320
110	320
111	320
112	320
113	320
114	320
115	320
116	320
117	320
118	320
119	320
120	320
121	320
122	320
123	320
124	320
125	320
126	320
127	320
128	320
129	320
130	320
131	320
132	320
133	320
134	320
135	320
136	320
137	320
138	320
139	320
140	320
141	320
142	320
143	320
144	320
145	320
146	320
147	320
148	320
149	320
150	320
151	320
152	320
153	320
154	320
155	320
156	320
157	320
158	320
159	320
160	320
161	320
162	320
163	320
164	320
165	320
166	320
167	320
168	320
169	320
170	320
171	320
172	320
173	320
174	320
175	320
176	320
177	320
178	320
179	320
180	320
100	321
100	322
100	323
100	324
100	325
100	326
100	327
100	328
100	329
100	330
100	331
100	332
100	333
100	334
100	335
100	336
100	337
100	338
100	339
100	340
100	341
100	342
100	343
100	344
100	345
100	346
100	347
100	348
100	349
100	350
100	351
100	352
100	353
100	354
100	355
100	356
100	357
100	358
100	359
100	360
100	361
100	362
100	363
100	364
100	365
100	366
100	367
100	368
100	369
100	370
100	371
100	372
100	373
100	374
100	375
100	376
100	377
100	378
100	379
100	380
100	381
100	382
100	383
100	384
100	385
100	386
100	387
100	388
100	389
100	390
100	391
100	392
100	393
100	394
100	395
100	396
100	397
100	398
100	399
20	400
21	400
22	400
23	400
24	400
25	400
26	400
27	400
28	400
29	400
30	400
31	400
32	400
33	400
34	400
35	400
36	400
37	400
38	400
39	400
40	400
41	400
42	400
43	400
44	400
45	400
46	400
47	400
48	400
49	400
50	400
51	400
52	400
53	400
54	400
55	400
56	400
57	400
58	400
59	400
60	400
61	400
62	400
63	400
64	400
65	400
66	400
67	400
68	400
69	400
70	400
71	400
72	400
73	400
74	400
75	400
76	400
77	400
78	400
79	400
80	400
81	400
82	400
83	400
84	400
85	400
86	400
87	400
88	400
89	400
90	400
91	400
92	400
93	400
94	400
95	400
96	400
97	400
98	400
99	400
100	400
100	401
100	402
100	403
100	404
100	405
100	406
100	407
100	408
100	409
100	410
100	411
100	412
100	413
100	414
100	415
100	416
100	417
100	418
100	419
100	420
100	421
100	422
100	423
100	424
100	425
100	426
100	427
100	428
100	429
100	430
100	431
100	432
100	433
100	434
100	435
100	436
100	437
100	438
100	439
100	440
100	441
100	442
100	443
100	444
100	445
100	446
100	447
100	448
100	449
100	450
100	451
100	452
100	453
100	454
100	455
100	456
100	457
100	458
100	459
100	460
100	461
100	462
100	463
100	464
100	465
100	466
100	467
100	468
100	469
100	470
100	471
100	472
100	473
100	474
100	475
100	476
100	477
100	478
100	479
100	480
101	480
102	480
103	480
104	480
105	480
106	480
107	480
108	480
109	480
110	480
111	480
112	480
113	480
114	480
115	480
116	480
117	480
118	480
119	480
120	480
121	480
122	480
123	480
124	480
125	480
126	480
127	480
128	480
129	480
130	480
131	480
132	480
133	480
134	480
135	480
136	480
137	480
138	480
139	480
140	480
141	480
142	480
143	480
144	480
145	480
146	480
147	480
148	480
149	480
150	480
151	480
152	480
153	480
154	480
155	480
156	480
157	480
158	480
159	480
160	480
161	480
162	480
163	480
164	480
165	480
166	480
167	480
168	480
169	480
170	480
171	480
172	480
173	480
174	480
175	480
176	480
177	480
178	480
179	480
180	480
100	481
100	482
100	483
100	484
100	485
100	486
100	487
100	488
100	489
100	490
100	491
100	492
100	493
100	494
100	495
100	496
100	497
100	498
100	499
100	500
100	501
100	502
100	503
100	504
100	505
100	506
100	507
100	508
100	509
100	510
100	511
100	512
100	513
100	514
100	515
100	516
100	517
100	518
100	519
100	520
100	521
100	522
100	523
100	524
100	525
100	526
100	527
100	528
100	529
100	530
100	531
100	532
100	533
100	534
100	535
100	536
100	537
100	538
100	539
100	540
100	541
100	542
100	543
100	544
100	545
100	546
100	547
100	548
100	549
100	550
100	551
100	552
100	553
100	554
100	555
100	556
100	557
100	558
100	559
20	560
21	560
22	560
23	560
24	560
25	560
26	560
27	560
28	560
29	560
30	560
31	560
32	560
33	560
34	560
35	560
36	560
37	560
38	560
39	560
40	560
41	560
42	560
43	560
44	560
45	560
46	560
47	560
48	560
49	560
50	560
51	560
52	560
53	560
54	560
55	560
56	560
57	560
58	560
59	560
60	560
61	560
62	560
63	560
64	560
65	560
66	560
67	560
68	560
69	560
70	560
71	560
72	560
73	560
74	560
75	560
76	560
77	560
78	560
79	560
80	560
81	560
82	560
83	560
84	560
85	560
86	560
87	560
88	560
89	560
90	560
91	560
92	560
93	560
94	560
95	560
96	560
97	560
98	560
99	560
100	560
100	561
100	562
100	563
100	564
100	565
100	566
100	567
100	568
100	569
100	570
100	571
100	572
100	573
100	574
100	575
100	576
100	577
100	578
100	579
100	580
100	581
100	582
100	583
100	584
100	585
100	586
100	587
100	588
100	589
100	590
100	591
100	592
100	593
100	594
100	595
100	596
100	597
100	598
100	599
100	600
100	601
100	602
100	603
100	604
100	605
100	606
100	607
100	608
100	609
100	610
100	611
100	612
100	613
100	614
100	615
100	616
100	617
100	618
100	619
100	620
100	621
100	622
100	623
100	624
100	625
100	626
100	627
100	628
100	629
100	630
100	631
100	632
100	633
100	634
100	635
100	636
100	637
100	638
100	639
100	640
101	640
102	640
103	640
104	640
105	640
106	640
107	640
108	640
109	640
110	640
111	640
112	640
113	640
114	640
115	640
116	640
117	640
118	640
119	640
120	640
121	640
122	640
123	640
124	640
125	640
126	640
127	640
128	640
129	640
130	640
131	640
132	640
133	640
134	640
135	640
136	640
137	640
138	640
139	640
140	640
141	640
142	640
143	640
144	640
145	640
146	640
147	640
148	640
149	640
150	640
151	640
152	640
153	640
154	640
155	640
156	640
157	640
158	640
159	640
160	640
161	640
162	640
163	640
164	640
165	640
166	640
167	640
168	640
169	640
170	640
171	640
172	640
173	640
174	640
175	640
176	640
177	640
178	640
179	640
180	640
100	641
100	642
100	643
100	644
100	645
100	646
100	647
100	648
100	649
100	650
100	651
100	652
100	653
100	654
100	655
100	656
100	657
100	658
100	659
100	660
100	661
100	662
100	663
100	664
100	665
100	666
100	667
100	668
100	669
100	670
100	671
100	672
100	673
100	674
100	675
100	676
100	677
100	678
100	679
100	680
100	681
100	682
100	683
100	684
100	685
100	686
100	687
100	688
100	689
100	690
100	691
100	692
100	693
100	694
100	695
100	696
100	697
100	698
100	699
100	700
100	701
100	702
100	703
100	704
100	705
100	706
100	707
100	708
100	709
100	710
100	711
100	712
100	713
100	714
100	715
100	716
100	717
100	718
100	719
20	720
21	720
22	720
23	720
24	720
25	720
26	720
27	720
28	720
29	720
30	720
31	720
32	720
33	720
34	720
35	720
36	720
37	720
38	720
39	720
40	720
41	720
42	720
43	720
44	720
45	720
46	720
47	720
48	720
49	720
50	720
51	720
52	720
53	720
54	720
55	720
56	720
57	720
58	720
59	720
60	720
61	720
62	720
63	720
64	720
65	720
66	720
67	720
68	720
69	720
70	720
71	720
72	720
73	720
74	720
75	720
76	720
77	720
78	720
79	720
80	720
81	720
82	720
83	720
84	720
85	720
86	720
87	720
88	720
89	720
90	720
91	720
92	720
93	720
94	720
95	720
96	720
97	720
98	720
99	720
100	720
100	721
100	722
100	723
100	724
100	725
100	726
100	727
100	728
100	729
100	730
100	731
100	732
100	733
100	734
100	735
100	736
100	737
100	738
100	739
100	740
100	741
100	742
100	743
100	744
100	745
100	746
100	747
100	748
100	749
100	750
100	751
100	752
100	753
100	754
100	755
100	756
100	757
100	758
100	759
100	760
100	761
100	762
100	763
100	764
100	765
100	766
100	767
100	768
100	769
100	770
100	771
100	772
100	773
100	774
100	775
100	776
100	777
100	778
100	779
100	780
100	781
100	782
100	783
100	784
100	785
100	786
100	787
100	788
100	789
100	790
100	791
100	792
100	793
100	794
100	795
100	796
100	797
100	798
100	799
100	800


stream20
20	1
21	1
22	1
23	1
24	1
25	1
26	1
27	1
28	1
29	1
30	1
31	1
32	1
33	1
34	1
35	1
36	1
37	1
38	1
39	1
40	1
41	1
42	1
43	1
44	1
45	1
46	1
47	1
48	1
49	1
50	1
51	1
52	1
53	1
54	1
55	1
56	1
57	1
58	1
59	1
60	1
40	2
40	3
40	4
40	5
40	6
40	7
40	8
40	9
40	10
40	11
40	12
40	13
40	14
40	15
40	16
40	17
40	18
40	19
40	20
40	21
40	22
40	23
40	24
40	25
40	26
40	27
40	28
40	29
40	30
40	31
40	32
40	33
40	34
40	35
40	36
40	37
40	38
40	39
1	40
2	40
3	40
4	40
5	40
6	40
7	40
8	40
9	40
10	40
11	40
12	40
13	40
14	40
15	40
16	40
17	40
18	40
19	40
20	40
21	40
22	40
23	40
24	40
25	40
26	40
27	40
28	40
29	40
30	40
31	40
32	40
33	40
34	40
35	40
36	40
37	40
38	40
39	40
40	40
40	41
40	42
40	43
40	44
40	45
40	46
40	47
40	48
40	49
40	50
40	51
40	52
40	53
40	54
40	55
40	56
40	57
40	58
40	59
40	60
40	61
40	62
40	63
40	64
40	65
40	66
40	67
40	68
40	69
40	70
40	71
40	72
40	73
40	74
40	75
40	76
40	77
40	78
40	79
40	80
41	80
42	80
43	80
44	80
45	80
46	80
47	80
48	80
49	80
50	80
51	80
52	80
53	80
54	80
55	80
56	80
57	80
58	80
59	80
60	80
61	80
62	80
63	80
64	80
65	80
66	80
67	80
68	80
69	80
70	80
71	80
72	80
73	80
74	80
75	80
76	80
77	80
78	80
79	80
80	80
40	81
40	82
40	83
40	84
40	85
40	86
40	87
40	88
40	89
40	90
40	91
40	92
40	93
40	94
40	95
40	96
40	97
40	98
40	99
40	100
40	101
40	102
40	103
40	104
40	105
40	106
40	107
40	108
40	109
40	110
40	111
40	112
40	113
40	114
40	115
40	116
40	117
40	118
40	119
1	120
2	120
3	120
4	120
5	120
6	120
7	120
8	120
9	120
10	120
11	120
12	120
13	120
14	120
15	120
16	120
17	120
18	120
19	120
20	120
21	120
22	120
23	120
24	120
25	120
26	120
27	120
28	120
29	120
30	120
31	120
32	120
33	120
34	120
35	120
36	120
37	120
38	120
39	120
40	120
40	121
40	122
40	123
40	124
40	125
40	126
40	127
40	128
40	129
40	130
40	131
40	132
40	133
40	134
40	135
40	136
40	137
40	138
40	139
40	140
40	141
40	142
40	143
40	144
40	145
40	146
40	147
40	148
40	149
40	150
40	151
40	152
40	153
40	154
40	155
40	156
40	157
40	158
40	159
40	160
41	160
42	160
43	160
44	160
45	160
46	160
47	160
48	160
49	160
50	160
51	160
52	160
53	160
54	160
55	160
56	160
57	160
58	160
59	160
60	160
61	160
62	160
63	160
64	160
65	160
66	160
67	160
68	160
69	160
70	160
71	160
72	160
73	160
74	160
75	160
76	160
77	160
78	160
79	160
80	160
40	161
40	162
40	163
40	164
40	165
40	166
40	167
40	168
40	169
40	170
40	171
40	172
40	173
40	174
40	175
40	176
40	177
40	178
40	179
40	180
40	181
40	182
40	183
40	184
40	185
40	186
40	187
40	188
40	189
40	190
40	191
40	192
40	193
40	194
40	195
40	196
40	197
40	198
40	199
1	200
2	200
3	200
4	200
5	200
6	200
7	200
8	200
9	200
10	200
11	200
12	200
13	200
14	200
15	200
16	200
17	200
18	200
19	200
20	200
21	200
22	200
23	200
24	200
25	200
26	200
27	200
28	200
29	200
30	200
31	200
32	200
33	200
34	200
35	200
36	200
37	200
38	200
39	200
40	200
40	201
40	202
40	203
40	204
40	205
40	206
40	207
40	208
40	209
40	210
40	211
40	212
40	213
40	214
40	215
40	216
40	217
40	218
40	219
40	220
40	221
40	222
40	223
40	224
40	225
40	226
40	227
40	228
40	229
40	230
40	231
40	232
40	233
40	234
40	235
40	236
40	237
40	238
40	239
40	240
41	240
42	240
43	240
44	240
45	240
46	240
47	240
48	240
49	240
50	240
51	240
52	240
53	240
54	240
55	240
56	240
57	240
58	240
59	240
60	240
61	240
62	240
63	240
64	240
65	240
66	240
67	240
68	240
69	240
70	240
71	240
72	240
73	240
74	240
75	240
76	240
77	240
78	240
79	240
80	240
40	241
40	242
40	243
40	244
40	245
40	246
40	247
40	248
40	249
40	250
40	251
40	252
40	253
40	254
40	255
40	256
40	257
40	258
40	259
40	260
40	261
40	262
40	263
40	264
40	265
40	266
40	267
40	268
40	269
40	270
40	271
40	272
40	273
40	274
40	275
40	276
40	277
40	278
40	279
1	280
2	280
3	280
4	280
5	280
6	280
7	280
8	280
9	280
10	280
11	280
12	280
13	280
14	280
15	280
16	280
17	280
18	280
19	280
20	280
21	280
22	280
23	280
24	280
25	280
26	280
27	280
28	280
29	280
30	280
31	280
32	280
33	280
34	280
35	280
36	280
37	280
38	280
39	280
40	280
40	281
40	282
40	283
40	284
40	285
40	286
40	287
40	288
40	289
40	290
40	291
40	292
40	293
40	294
40	295
40	296
40	297
40	298
40	299
40	300
40	301
40	302
40	303
40	304
40	305
40	306
40	307
40	308
40	309
40	310
40	311
40	312
40	313
40	314
40	315
40	316
40	317
40	318
40	319
40	320
41	320
42	320
43	320
44	320
45	320
46	320
47	320
48	320
49	320
50	320
51	320
52	320
53	320
54	320
55	320
56	320
57	320
58	320
59	320
60	320
61	320
62	320
63	320
64	320
65	320
66	320
67	320
68	320
69	320
70	320
71	320
72	320
73	320
74	320
75	320
76	320
77	320
78	320
79	320
80	320
40	321
40	322
40	323
40	324
40	325
40	326
40	327
40	328
40	329
40	330
40	331
40	332
40	333
40	334
40	335
40	336
40	337
40	338
40	339
40	340
40	341
40	342
40	343
40	344
40	345
40	346
40	347
40	348
40	349
40	350
40	351
40	352
40	353
40	354
40	355
40	356
40	357
40	358
40	359
1	360
2	360
3	360
4	360
5	360
6	360
7	360
8	360
9	360
10	360
11	360
12	360
13	360
14	360
15	360
16	360
17	360
18	360
19	360
20	360
21	360
22	360
23	360
24	360
25	360
26	360
27	360
28	360
29	360
30	360
31	360
32	360
33	360
34	360
35	360
36	360
37	360
38	360
39	360
40	360
40	361
40	362
40	363
40	364
40	365
40	366
40	367
40	368
40	369
40	370
40	371
40	372
40	373
40	374
40	375
40	376
40	377
40	378
40	379
40	380
40	381
40	382
40	383
40	384
40	385
40	386
40	387
40	388
40	389
40	390
40	391
40	392
40	393
40	394
40	395
40	396
40	397
40	398
40	399
40	400
41	400
42	400
43	400
44	400
45	400
46	400
47	400
48	400
49	400
50	400
51	400
52	400
53	400
54	400
55	400
56	400
57	400
58	400
59	400
60	400
61	400
62	400
63	400
64	400
65	400
66	400
67	400
68	400
69	400
70	400
71	400
72	400
73	400
74	400
75	400
76	400
77	400
78	400
79	400
80	400
40	401
40	402
40	403
40	404
40	405
40	406
40	407
40	408
40	409
40	410
40	411
40	412
40	413
40	414
40	415
40	416
40	417
40	418
40	419
40	420
40	421
40	422
40	423
40	424
40	425
40	426
40	427
40	428
40	429
40	430
40	431
40	432
40	433
40	434
40	435
40	436
40	437
40	438
40	439
1	440
2	440
3	440
4	440
5	440
6	440
7	440
8	440
9	440
10	440
11	440
12	440
13	440
14	440
15	440
16	440
17	440
18	440
19	440
20	440
21	440
22	440
23	440
24	440
25	440
26	440
27	440
28	440
29	440
30	440
31	440
32	440
33	440
34	440
35	440
36	440
37	440
38	440
39	440
40	440
40	441
40	442
40	443
40	444
40	445
40	446
40	447
40	448
40	449
40	450
40	451
40	452
40	453
40	454
40	455
40	456
40	457
40	458
40	459
40	460
40	461
40	462
40	463
40	464
40	465
40	466
40	467
40	468
40	469
40	470
40	471
40	472
40	473
40	474
40	475
40	476
40	477
40	478
40	479
40	480
41	480
42	480
43	480
44	480
45	480
46	480
47	480
48	480
49	480
50	480
51	480
52	480
53	480
54	480
55	480
56	480
57	480
58	480
59	480
60	480
61	480
62	480
63	480
64	480
65	480
66	480
67	480
68	480
69	480
70	480
71	480
72	480
73	480
74	480
75	480
76	480
77	480
78	480
79	480
80	480
40	481
40	482
40	483
40	484
40	485
40	486
40	487
40	488
40	489
40	490
40	491
40	492
40	493
40	494
40	495
40	496
40	497
40	498
40	499
40	500
40	501
40	502
40	503
40	504
40	505
40	506
40	507
40	508
40	509
40	510
40	511
40	512
40	513
40	514
40	515
40	516
40	517
40	518
40	519
1	520
2	520
3	520
4	520
5	520
6	520
7	520
8	520
9	520
10	520
11	520
12	520
13	520
14	520
15	520
16	520
17	520
18	520
19	520
20	520
21	520
22	520
23	520
24	520
25	520
26	520
27	520
28	520
29	520
30	520
31	520
32	520
33	520
34	520
35	520
36	520
37	520
38	520
39	520
40	520
40	521
40	522
40	523
40	524
40	525
40	526
40	527
40	528
40	529
40	530
40	531
40	532
40	533
40	534
40	535
40	536
40	537
40	538
40	539
40	540
40	541
40	542
40	543
40	544
40	545
40	546
40	547
40	548
40	549
40	550
40	551
40	552
40	553
40	554
40	555
40	556
40	557
40	558
40	559
40	560
41	560
42	560
43	560
44	560
45	560
46	560
47	560
48	560
49	560
50	560
51	560
52	560
53	560
54	560
55	560
56	560
57	560
58	560
59	560
60	560
61	560
62	560
63	560
64	560
65	560
66	560
67	560
68	560
69	560
70	560
71	560
72	560
73	560
74	560
75	560
76	560
77	560
78	560
79	560
80	560
40	561
40	562
40	563
40	564
40	565
40	566
40	567
40	568
40	569
40	570
40	571
40	572
40	573
40	574
40	575
40	576
40	577
40	578
40	579
40	580
40	581
40	582
40	583
40	584
40	585
40	586
40	587
40	588
40	589
40	590
40	591
40	592
40	593
40	594
40	595
40	596
40	597
40	598
40	599
1	600
2	600
3	600
4	600
5	600
6	600
7	600
8	600
9	600
10	600
11	600
12	600
13	600
14	600
15	600
16	600
17	600
18	600
19	600
20	600
21	600
22	600
23	600
24	600
25	600
26	600
27	600
28	600
29	600
30	600
31	600
32	600
33	600
34	600
35	600
36	600
37	600
38	600
39	600
40	600
40	601
40	602
40	603
40	604
40	605
40	606
40	607
40	608
40	609
40	610
40	611
40	612
40	613
40	614
40	615
40	616
40	617
40	618
40	619
40	620
40	621
40	622
40	623
40	624
40	625
40	626
40	627
40	628
40	629
40	630
40	631
40	632
40	633
40	634
40	635
40	636
40	637
40	638
40	639
40	640
41	640
42	640
43	640
44	640
45	640
46	640
47	640
48	640
49	640
50	640
51	640
52	640
53	640
54	640
55	640
56	640
57	640
58	640
59	640
60	640
61	640
62	640
63	640
64	640
65	640
66	640
67	640
68	640
69	640
70	640
71	640
72	640
73	640
74	640
75	640
76	640
77	640
78	640
79	640
80	640
40	641
40	642
40	643
40	644
40	645
40	646
40	647
40	648
40	649
40	650
40	651
40	652
40	653
40	654
40	655
40	656
40	657
40	658
40	659
40	660
40	661
40	662
40	663
40	664
40	665
40	666
40	667
40	668
40	669
40	670
40	671
40	672
40	673
40	674
40	675
40	676
40	677
40	678
40	679
1	680
2	680
3	680
4	680
5	680
6	680
7	680
8	680
9	680
10	680
11	680
12	680
13	680
14	680
15	680
16	680
17	680
18	680
19	680
20	680
21	680
22	680
23	680
24	680
25	680
26	680
27	680
28	680
29	680
30	680
31	680
32	680
33	680
34	680
35	680
36	680
37	680
38	680
39	680
40	680
40	681
40	682
40	683
40	684
40	685
40	686
40	687
40	688
40	689
40	690
40	691
40	692
40	693
40	694
40	695
40	696
40	697
40	698
40	699
40	700
40	701
40	702
40	703
40	704
40	705
40	706
40	707
40	708
40	709
40	710
40	711
40	712
40	713
40	714
40	715
40	716
40	717
40	718
40	719
40	720
41	720
42	720
43	720
44	720
45	720
46	720
47	720
48	720
49	720
50	720
51	720
52	720
53	720
54	720
55	720
56	720
57	720
58	720
59	720
60	720
61	720
62	720
63	720
64	720
65	720
66	720
67	720
68	720
69	720
70	720
71	720
72	720
73	720
74	720
75	720
76	720
77	720
78	720
79	720
80	720
40	721
40	722
40	723
40	724
40	725
40	726
40	727
40	728
40	729
40	730
40	731
40	732
40	733
40	734
40	735
40	736
40	737
40	738
40	739
40	740
40	741
40	742
40	743
40	744
40	745
40	746
40	747
40	748
40	749
40	750
40	751
40	752
40	753
40	754
40	755
40	756
40	757
40	758
40	759
1	760
2	760
3	760
4	760
5	760
6	760
7	760
8	760
9	760
10	760
11	760
12	760
13	760
14	760
15	760
16	760
17	760
18	760
19	760
20	760
21	760
22	760
23	760
24	760
25	760
26	760
27	760
28	760
29	760
30	760
31	760
32	760
33	760
34	760
35	760
36	760
37	760
38	760
39	760
40	760
40	761
40	762
40	763
40	764
40	765
40	766
40	767
40	768
40	769
40	770
40	771
40	772
40	773
40	774
40	775
40	776
40	777
40	778
40	779
40	780
40	781
40	782
40	783
40	784
40	785
40	786
40	787
40	788
40	789
40	790
40	791
40	792
40	793
40	794
40	795
40	796
40	797
40	798
40	799
40	800
0	40
0	120
0	200
0	280
0	360
0	440
0	520
0	600
0	680
0	760


stream10c
0	7
0	8
0	9
0	10
0	11
0	12
0	13
0	14
0	15
0	16
0	17
0	18
0	19
0	20
0	21
0	22
0	23
0	24
0	25
0	26
0	27
0	28
0	29
0	30
0	31
0	32
0	33
0	34
0	35
0	36
0	37
0	38
0	39
0	40
0	41
0	42
1	42
2	42
3	42
4	42
5	42
6	42
7	42
8	42
9	42
10	42
11	42
12	42
13	42
14	42
15	42
16	42
17	42
18	42
19	42
20	42
21	42
21	43
21	44
21	45
21	46
21	47
21	48
21	49
21	50
21	51
21	52
21	53
21	54
21	55
21	56
21	57
21	58
21	59
21	60
21	61
21	62
21	63
21	64
21	65
21	66
21	67
21	68
21	69
21	70
21	71
21	72
21	73
21	74
21	75
21	76
21	77
21	78
21	79
21	80
21	81
21	82
21	83
21	84
22	42
22	84
23	42
23	84
24	42
24	84
25	42
25	84
26	42
26	84
27	42
27	84
28	42
28	84
29	42
29	84
30	42
30	84
31	42
31	84
32	42
32	84
33	42
33	84
34	42
34	84
35	42
35	84
36	42
36	84
37	42
37	84
38	42
38	84
39	42
39	84
40	42
40	84
41	42
41	84
42	11
42	12
42	13
42	14
42	15
42	16
42	17
42	18
42	19
42	20
42	21
42	22
42	23
42	24
42	25
42	26
42	27
42	28
42	29
42	30
42	31
42	32
42	33
42	34
42	35
42	36
42	37
42	38
42	39
42	40
42	41
42	42
42	84
43	84
44	84
45	84
46	84
47	84
48	84
49	84
50	84
51	84
52	84
53	84
54	84
55	84
56	84
57	84
58	84
59	84
60	84
61	84
62	84
63	84
63	85
63	86
63	87
63	88
63	89
63	90
63	91
63	92
63	93
63	94
63	95
63	96
63	97
63	98
63	99
63	100
63	101
63	102
63	103
63	104
63	105
63	106
63	107
63	108
63	109
63	110
63	111
63	112
63	113
63	114
63	115
63	116
63	117
63	118
63	119
63	120
63	121
63	122
63	123
63	124
63	125
63	126
64	84
64	126
65	84
65	126
66	84
66	126
67	84
67	126
68	84
68	126
69	84
69	126
70	84
70	126
71	84
71	126
72	84
72	126
73	84
73	126
74	84
74	126
75	84
75	126
76	84
76	126
77	84
77	126
78	84
78	126
79	84
79	126
80	84
80	126
81	84
81	126
82	84
82	126
83	84
83	126
84	11
84	12
84	13
84	14
84	15
84	16
84	17
84	18
84	19
84	20
84	21
84	22
84	23
84	24
84	25
84	26
84	27
84	28
84	29
84	30
84	31
84	32
84	33
84	34
84	35
84	36
84	37
84	38
84	39
84	40
84	41
84	42
84	84
84	126
85	42
85	84
85	126
86	42
86	84
86	126
87	42
87	84
87	126
88	42
88	84
88	126
89	42
89	84
89	126
90	42
90	84
90	126
91	42
91	84
91	126
92	42
92	84
92	126
93	42
93	84
93	126
94	42
94	84
94	126
95	42
95	84
95	126
96	42
96	84
96	126
97	42
97	84
97	126
98	42
98	84
98	126
99	42
99	84
99	126
100	42
100	84
100	126
101	42
101	84
101	126
102	42
102	84
102	126
103	42
103	84
103	126
104	42
104	84
104	126
105	42
105	43
105	44
105	45
105	46
105	47
105	48
105	49
105	50
105	51
105	52
105	53
105	54
105	55
105	56
105	57
105	58
105	59
105	60
105	61
105	62
105	63
105	64
105	65
105	66
105	67
105	68
105	69
105	70
105	71
105	72
105	73
105	74
105	75
105	76
105	77
105	78
105	79
105	80
105	81
105	82
105	83
105	84
105	126
106	42
106	126
107	42
107	126
108	42
108	126
109	42
109	126
110	42
110	126
111	42
111	126
112	42
112	126
113	42
113	126
114	42
114	126
115	42
115	126
116	42
116	126
117	42
117	126
118	42
118	126
119	42
119	126
120	42
120	126
121	42
121	126
122	42
122	126
123	42
123	126
124	42
124	126
125	42
125	126
126	11
126	12
126	13
126	14
126	15
126	16
126	17
126	18
126	19
126	20
126	21
126	22
126	23
126	24
126	25
126	26
126	27
126	28
126	29
126	30
126	31
126	32
126	33
126	34
126	35
126	36
126	37
126	38
126	39
126	40
126	41
126	42
126	126
127	126
128	126
129	126
130	126
131	126
132	126
133	126
134	126
135	126
136	126
137	126
138	126
139	126
140	126
141	126
142	126
143	126
144	126
145	126
146	126
147	126
148	126
149	126
150	126
151	126
152	126
153	126
154	126
155	126
156	126
157	126
158	126
159	126
160	126
161	126
162	126
163	126
164	126
165	126
166	126
167	126
168	11
168	12
168	13
168	14
168	15
168	16
168	17
168	18
168	19
168	20
168	21
168	22
168	23
168	24
168	25
168	26
168	27
168	28
168	29
168	30
168	31
168	32
168	33
168	34
168	35
168	36
168	37
168	38
168	39
168	40
168	41
168	42
168	126
169	42
169	126
170	42
170	126
171	42
171	126
172	42
172	126
173	42
173	126
174	42
174	126
175	42
175	126
176	42
176	126
177	42
177	126
178	42
178	126
179	42
179	126
180	42
180	126
181	42
181	126
182	42
182	126
183	42
183	126
184	42
184	126
185	42
185	126
186	42
186	126
187	42
187	126
188	42
188	126
189	42
189	43
189	44
189	45
189	46
189	47
189	48
189	49
189	50
189	51
189	52
189	53
189	54
189	55
189	56
189	57
189	58
189	59
189	60
189	61
189	62
189	63
189	64
189	65
189	66
189	67
189	68
189	69
189	70
189	71
189	72
189	73
189	74
189	75
189	76
189	77
189	78
189	79
189	80
189	81
189	82
189	83
189	84
189	126
190	42
190	84
190	126
191	42
191	84
191	126
192	42
192	84
192	126
193	42
193	84
193	126
194	42
194	84
194	126
195	42
195	84
195	126
196	42
196	84
196	126
197	42
197	84
197	126
198	42
198	84
198	126
199	42
199	84
199	126
200	42
200	84
200	126
201	42
201	84
201	126
202	42
202	84
202	126
203	42
203	84
203	126
204	42
204	84
204	126
205	42
205	84
205	126
206	42
206	84
206	126
207	42
207	84
207	126
208	42
208	84
208	126
209	42
209	84
209	126
210	11
210	12
210	13
210	14
210	15
210	16
210	17
210	18
210	19
210	20
210	21
210	22
210	23
210	24
210	25
210	26
210	27
210	28
210	29
210	30
210	31
210	32
210	33
210	34
210	35
210	36
210	37
210	38
210	39
210	40
210	41
210	42
210	84
210	126
211	84
211	126
212	84
212	126
213	84
213	126
214	84
214	126
215	84
215	126
216	84
216	126
217	84
217	126
218	84
218	126
219	84
219	126
220	84
220	126
221	84
221	126
222	84
222	126
223	84
223	126
224	84
224	126
225	84
225	126
226	84
226	126
227	84
227	126
228	84
228	126
229	84
229	126
230	84
230	126
231	84
231	85
231	86
231	87
231	88
231	89
231	90
231	91
231	92
231	93
231	94
231	95
231	96
231	97
231	98
231	99
231	100
231	101
231	102
231	103
231	104
231	105
231	106
231	107
231	108
231	109
231	110
231	111
231	112
231	113
231	114
231	115
231	116
231	117
231	118
231	119
231	120
231	121
231	122
231	123
231	124
231	125
231	126
232	84
232	126
233	84
233	126
234	84
234	126
235	84
235	126
236	84
236	126
237	84
237	126
238	84
238	126
239	84
239	126
240	84
240	126
241	84
241	126
242	84
242	126
243	84
243	126
244	84
244	126
245	84
245	126
246	84
246	126
247	84
247	126
248	84
248	126
249	84
249	126
250	84
250	126
251	84
251	126
252	11
252	12
252	13
252	14
252	15
252	16
252	17
252	18
252	19
252	20
252	21
252	22
252	23
252	24
252	25
252	26
252	27
252	28
252	29
252	30
252	31
252	32
252	33
252	34
252	35
252	36
252	37
252	38
252	39
252	40
252	41
252	42
252	84
252	126
253	42
253	84
253	126
254	42
254	84
254	126
255	42
255	84
255	126
256	42
256	84
256	126
257	42
257	84
257	126
258	42
258	84
258	126
259	42
259	84
259	126
260	42
260	84
260	126
261	42
261	84
261	126
262	42
262	84
262	126
263	42
263	84
263	126
264	42
264	84
264	126
265	42
265	84
265	126
266	42
266	84
266	126
267	42
267	84
267	126
268	42
268	84
268	126
269	42
269	84
269	126
270	42
270	84
270	126
271	42
271	84
271	126
272	42
272	84
272	126
273	42
273	43
273	44
273	45
273	46
273	47
273	48
273	49
273	50
273	51
273	52
273	53
273	54
273	55
273	56
273	57
273	58
273	59
273	60
273	61
273	62
273	63
273	64
273	65
273	66
273	67
273	68
273	69
273	70
273	71
273	72
273	73
273	74
273	75
273	76
273	77
273	78
273	79
273	80
273	81
273	82
273	83
273	84
273	126
274	42
274	126
275	42
275	126
276	42
276	126
277	42
277	126
278	42
278	126
279	42
279	126
280	42
280	126
281	42
281	126
282	42
282	126
283	42
283	126
284	42
284	126
285	42
285	126
286	42
286	126
287	42
287	126
288	42
288	126
289	42
289	126
290	42
290	126
291	42
291	126
292	42
292	126
293	42
293	126
294	11
294	12
294	13
294	14
294	15
294	16
294	17
294	18
294	19
294	20
294	21
294	22
294	23
294	24
294	25
294	26
294	27
294	28
294	29
294	30
294	31
294	32
294	33
294	34
294	35
294	36
294	37
294	38
294	39
294	40
294	41
294	42
294	126
295	126
296	126
297	126
298	126
299	126
300	126
301	126
302	126
303	126
304	126
305	126
306	126
307	126
308	126
309	126
310	126
311	126
312	126
313	126
314	126
315	126
316	126
317	126
318	126
319	126
320	126
321	126
322	126
323	126
324	126
325	126
326	126
327	126
328	126
329	126
330	126
331	126
332	126
333	126
334	126
335	126
336	11
336	12
336	13
336	14
336	15
336	16
336	17
336	18
336	19
336	20
336	21
336	22
336	23
336	24