|
|
|
Copyright © 2002 by the author(s). Published here under license by The Resilience Alliance.
Go to the pdf version of this article.
The following is the established format for referencing this article:
Casagrandi, R. and S. Rinaldi. 2002. A theoretical approach to tourism sustainability. Conservation Ecology 6(1): 13. [online] URL: http://www.consecol.org/vol6/iss1/art13/
A version of this article in which text, figures, tables, and appendices are separate files may be found by following this link.
Report A Theoretical Approach to Tourism Sustainability Renato Casagrandi1 and Sergio Rinaldi2
1Dipartimento di Elettronica e Informazione, Politecnico di Milano; 2CIRITA, Politecnico di Milano
- Abstract
- Introduction
- A Minimal Model
- The Tourists
- The Environment
- The Capital
- The Tourist Destination Life Cycle
- Analysis of the Model
- Profitable, Compatible, and Sustainable Policies
- Conclusions
- Responses to this Article
- Acknowledgments
- Literature Cited
This paper shows that it is difficult, if not impossible, to formulate policies that guarantee that tourism can be maintained for a long time without severely impacting on the environment. The analysis is purely theoretical and is based on very simple and general assumptions about the interactions between the three main components of the system: the tourists, the environment, and the capital. These assumptions are encapsulated in a so-called minimal model, used to predict the economic and environmental impact of any given policy. This paper is of value for three reasons. First, it introduces the approach of minimal descriptive models in the context of tourism, which has traditionally been dominated by the use of black-box econometric models. Second, the specific results are quite interesting. We show, in fact, that tourism sustainability can be achieved, provided agents are prudent about reinvesting their profits and are willing to protect the environment, but that sustainability is very often at risk, because unforeseen shocks can easily trigger a switch from a profitable and compatible behavior to an unprofitable or incompatible one. These results are in line with conventional wisdom and observations, but the interesting fact is that here they are theoretically derived from a few very simple and abstract premises. Third, although not directly related to the problem of tourism but rather to the general topic of sustainability, this is one of the first times that the notion of sustainability, which is more and more pervasive in the field of resource management, is interpreted strictly in terms of the structural properties of the attractors of a dynamic system. This creates an important and promising bridge between sustainability and bifurcation theory, one of the most important areas of systems analysis.
KEY WORDS: bifurcation analysis, environment, model, nonlinear dynamics, sustainability, tourism.
Published: June 4, 2002
The tourism industry has increased considerably in recent decades and has become one of the main sources of income in many countries (Williams and Shaw 1988, Coccossis and Nijkamp 1995). For many tourist sites, the reward phase of development is characterized by a long and intense growth in infrastructure, superstructure, and facilities which, sooner or later, seriously impact on the environment, thus creating a critical situation. In fact, some destinations, after flourishing for a long time, have been abandoned by tourists in favor of more attractive sites newly available on the market (Butler 1991). In order to compensate for this instability, local agents may seek increased investment and develop special facilities to attract tourists. Sometimes they are successful, but at the expense of the environment, which may be severely degraded.
This paper shows why it is difficult, if not impossible, to formulate policies that guarantee that tourism can be maintained for a long time without severely impacting on the environment. The analysis is very abstract. It is not based on data of one or more specific cases, but on very simple and general assumptions about the interactions between three important components of the system: the tourists, the natural environment, and the capital. These assumptions are contained in a so-called minimal (or stylized) model which is used to predict the economic and environmental impact of any given policy. The approach we use here is similar to that used by Anderies (1998, 2000) to analyze agro-ecosystem dynamics. It is new within the context of tourism studies. As some extensive reviews on the topic clearly demonstrate (Witt and Witt 1995, Kulendran and King 1997), the classical models for tourism are black-box econometric models (aimed mainly at forecasting demand for travel services or the number of tourist arrivals as a function of income, transportation costs, relative prices, currency exchange rates, or some other “qualitative factors”) that do not, at least in the 100 papers reviewed by Lim (1997), take into account the environment. These econometric models have been employed with different techniques, either cointegration or least squares (Kulendran and Witt 2001), on data referring to various target places, ranging from the northeast of England (Seddighi and Shearing 1997) to Australia (Morley 1998) and from Barbados (Dharmaratne 1995) to Turkey (Akis 1998). The study we present, however, is carried out by varying some abstract but meaningful parameters that interpret the attitude of agents toward the two main conflicting objectives: economic development and environmental protection (Lindberg 1991, Smith and Eadington 1992). The results are in agreement with conventional wisdom and, more generally, confirm the impression that human short-sightedness and greed can make sustainability an unattainable goal (Ludwig et al.1993, Ludwig 1993, Arrow et al. 1995, Roe 1996, Brown et al. 1996).
The minimal model on which the analysis is based is so crude and abstract that it cannot represent any specific system in detail. Nevertheless, it incorporates the core features of many systems. The model refers to a generic site and has only three variables: the tourists T(t) present in the area at time t, the quality of the natural environment E(t) and the capital C(t) intended as structures for tourist activities. Note that C(t) refers to tangible assets and should not be confused with the flow of services provided to tourists. Although the choice of these three components is rather obvious, their description using a single variable definitely poses some problems. In fact, one might be reluctant to aggregate into a single variable tourists of different incomes, lifestyles, and socio-cultural backgrounds, or infrastructure ranging from hotels to parks and from sport facilities to transportation systems. The same holds true for the quality of the environment, which is very often a mix of such diverse indicators as air quality, water quality, biodiversity, and wildlife and landscape conservation. But this aggregation process is necessary, because we must keep the number of variables and parameters reasonably low in order to obtain a workable problem. Seasonal effects are not taken into account here, as we are interested only in the long-term behavior of the system.
For all these reasons, our minimal model cannot be considered an operational tool for managers, even if it will be used to predict the ultimate consequences of different development policies. The nature of the model is so abstract that these consequences will not point out new and intriguing suggestions of practical interest to managers, but, instead, will allow a theoretical derivation of a rich catalogue of development scenarios confirming empirically observed patterns (see below). The fact that the results we will derive are already known from history, confirms that general theories can sometimes be as powerful as empirical observations.
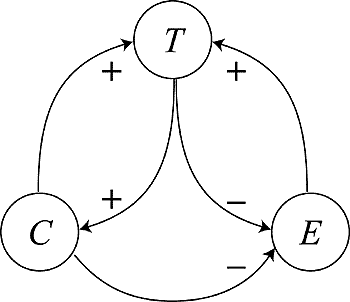
The interactions among the three components of our minimal model are sketched in Figure 1. Tourists (T) and tourist facilities (C) impact negatively on environmental quality (E), but environmental quality and infrastructure are attractive to tourists. The positive arrow from T to C represents the investment of part of the profits associated with tourism into new facilities for visitors. Below, we detail the functional forms of the influences depicted in Figure 1's graph.
|
Fig. 1. The interactions between the three components of our minimal model.
|
Imagine that tourists are asked to report on the attractiveness, A, of the sites they have visited and let us assume that these reports influence the decisions of potential new visitors (the “word-of-mouth” spread of information, Morley 1998). Measuring A in suitable units, we can then write that the rate of change of tourists at a given site is equal to the product TA, i.e.,
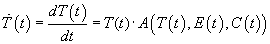 . . |
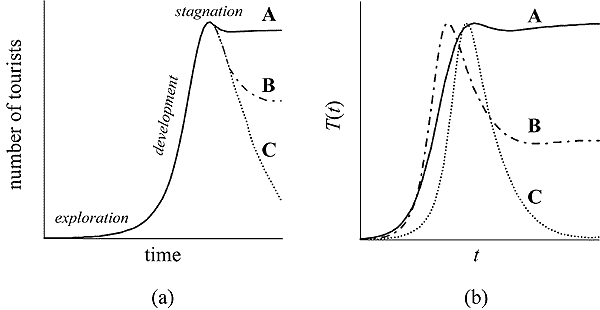
Of course, A must be a relative attractiveness, namely the difference between the absolute attractiveness, â, of the specific site (for which information on T, E, and C is available) and a reference value, a, which may be thought of as the expected attractiveness of a generic site (i.e., the average value of the attractiveness of all potential tourist sites). Thus
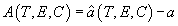 |
where a is influenced by a number of factors, including the price of alternative sites. In an abstract sense, a is a measure of the competition exerted by alternative tourist sites on the site under study. The attractiveness, â, being that perceived by the tourists, depends upon the culture of the tourists and, in particular, upon their sensitivity to the quality of the natural environment and their ability to detect it. It is the algebraic sum of three terms, because tourists can be sensitive to environmental quality, availability of facilities, and congestion. The attractiveness of the environment can be modeled as an increasing and saturating function of E. In the following, it will be described as a Monod function
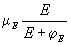 |
where μ E is the attractiveness associated with high environmental quality,
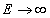 and
and 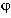 E is the half saturation constant, namely the environmental quality at which tourist satisfaction is half maximum. Thus, tourists characterized by low values of
E is the half saturation constant, namely the environmental quality at which tourist satisfaction is half maximum. Thus, tourists characterized by low values of 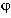 E
are satisfied by low environmental quality because they are unable to perceive environmental quality. For example, a tourist who is unable to perceive whether a river is polluted or not, will associate a constant attractiveness μE with the river regardless of its water quality, because
E
are satisfied by low environmental quality because they are unable to perceive environmental quality. For example, a tourist who is unable to perceive whether a river is polluted or not, will associate a constant attractiveness μE with the river regardless of its water quality, because
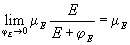 |
The second component of the attractiveness, namely that associated with infrastructure, can also be modeled through a Monod function of the estimated available facilities per capita
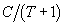 |
(1) |
i.e.,
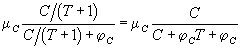 |
Notice that the attractiveness associated with the natural environment is a function of E and not of
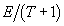 as prescribed by the theory of public goods and non-consumptive use (Herfindahl and Kneese 1974). In contrast, facilities are used by tourists and, therefore, the attractiveness associated with them, is a function of Eq. 1 above.
as prescribed by the theory of public goods and non-consumptive use (Herfindahl and Kneese 1974). In contrast, facilities are used by tourists and, therefore, the attractiveness associated with them, is a function of Eq. 1 above.
Finally, if we assume that congestion is proportional to T and that attractiveness is linearly decreasing with congestion, we end up with the following formula for â
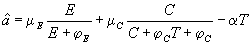 |
where the five parameters (μ E, 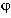 E,
μ C,
E,
μ C, 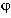 C, α) identify the culture of the tourist population. It is worth noting that the absolute attractiveness, â, of a site unexploited by tourism (C = T = 0) is positive and can be greater than the reference attractiveness, a. This means that the relative attractiveness, A, can be positive even when C = T = 0. This explains the initial phase of the well-known phenomenon that Butler (1980) called the “tourist-area cycle of evolution.”
C, α) identify the culture of the tourist population. It is worth noting that the absolute attractiveness, â, of a site unexploited by tourism (C = T = 0) is positive and can be greater than the reference attractiveness, a. This means that the relative attractiveness, A, can be positive even when C = T = 0. This explains the initial phase of the well-known phenomenon that Butler (1980) called the “tourist-area cycle of evolution.”
The quality of the environment E(t), in the absence of tourists and capital, is described by a classical logistic equation
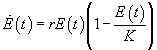 |
where the net growth rate, r, and the carrying capacity, K, are influenced by all activities except those related to the tourism industry. In other words, K is not the quality of the environment in unrealistic (i.e., pristine) condition, but, rather, the quality of the environment in the presence, in equilibrium, of all civil and industrial activities (except tourism) that characterize the site under study. If tourists and facilities impact negatively on the environment, the complete dynamics of E(t) are
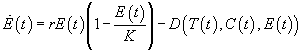 |
and
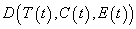 represents the flow of damages induced by tourism. Generally, this flow is positively correlated with tourists and capital. Moreover, the damage is greater when the environment is previously unexploited. The simplest functional form consistent with these properties is the following
represents the flow of damages induced by tourism. Generally, this flow is positively correlated with tourists and capital. Moreover, the damage is greater when the environment is previously unexploited. The simplest functional form consistent with these properties is the following
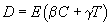 | (2) |
where the two parameters β and γ are positive. For example, hotel heating, which impacts on air pollution, has a first component that is basically independent of the number of tourists (heating the hall, the cafeteria, the rest-rooms, etc.) and a second component that is proportional to the number of visitors (heating the occupied guestrooms). This is perfectly consistent with Eq. 2. The same holds true for many other tourist facilities, such as ski lifts and discothèques (noise pollution), bus services (air pollution), artificial snow facilities (downstream water pollution), etc. In rare instances, β and γ may be negative; for example, when greater reclamation efforts are associated with tourism development. As a consequence of Eq. 2, if T and C were kept constant, the environment would still be described by a logistic equation
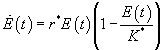 |
with
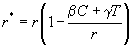 |
and
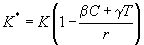 . . |
In other words, if β and γ are positive, tourism activities ( C and T) reduce the carrying capacity and the net growth rate of the environment in the same proportion.
Finally, the rate of change of capital is the difference between the investment flow, I, and a depreciation flow, which is proportional to C, i.e.,
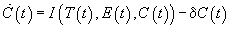 . . |
The parameter δ
must be very small because the degradation of tourist structures is very slow. The fact that the time constants of the socio-economic component are longer than those of the environmental component has been emphasized in Carpenter et al. (1999b). In our simulations, δ is one order of magnitude smaller than r, the net growth rate of the environment. The function I could be specified in many different ways to interpret different investment policies. Indeed, special constraints could be imposed on the function in order to avoid degenerate dynamics, as was done in Rinaldi et al. (1996) for a study on pollution control. Alternatively, the structure of the function 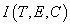 could be derived using optimization arguments, as in Gatto et al. (1991), Shah (1995) or Carpenter et al. (1999a). Here, we will assume that investments are a fixed proportion of total revenues generated by tourism activities and that such revenues are proportional to the number of tourists, i.e.,
could be derived using optimization arguments, as in Gatto et al. (1991), Shah (1995) or Carpenter et al. (1999a). Here, we will assume that investments are a fixed proportion of total revenues generated by tourism activities and that such revenues are proportional to the number of tourists, i.e.,
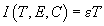 . . |
Thus, the parameter ε, or investment rate, increases along with local prices.
In conclusion, our minimal model turns out to be
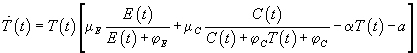 |
(3) |
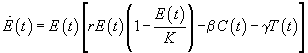 |
(4) |
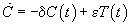 . . |
(5) |
This model is new, because it cannot be interpreted as a consumer-resource model. In fact, tourists and capital, which could be thought of as predators, do not increase in relation to the damages (predation) they cause to the environment.
The model has twelve parameters, of which the rate of investment ε is the one that local agents and decision makers can most easily control. Price control is also feasible in some cases but influences two parameters, namely ε and a. Reclamation of the environment gives rise to lower values of β and/or γ, which can become negative in extreme cases, while increased competition from alternative tourist sites can be viewed as an increase in a.
Because model 3-5 has been proposed on the basis of purely theoretical arguments, before proceeding any further, we should check if the model compares favorably with known data concerning development of a few representative tourist sites. This could be done by adjusting the parameters of the minimal model to a good fit with time series of tourist arrivals at different destination areas. But this might somehow suggest that the minimal model could be used by decision makers as an operational tool. In order to avoid this misleading impression, we have not performed any validation testing based on specific data sets. Instead, we show that the minimal model is capable of mimicking all the qualitatively different development scenarios discussed by Butler in his work on life cycle (Butler 1980), which has been widely accepted in a variety of empirical contexts. From the south coast of Britain (Agarwal 1997) to Indonesia (Dahles and Bras 1999), from Peru (O'Hare and Barrett 1997) to Swaziland (Harrison 1995), from Melanesia (Douglas 1997) to Cyprus (Akis et al. 1996), the curve of tourist arrivals over the years in every place seems to follow the pattern described by Butler. In order to study the initial phases of tourism in Europe, we should of course refer to works that date back at least to the beginning of the last century. In a paper that appeared in 1939 in the Scottish Geographical Magazine, Gilbert tried to understand why and how many seaside resorts in England were growing so fast. The development of infrastructure was indeed crucial to transform ancient ports or fishing harbors into seaside resorts. To give a vivid description of how tourism changes the nature of a place, Gilbert (1939) quoted part of an article published by The Times in 1860 (August 30 th):
Our seaport towns have been turned inside out. So infallible and unchanging are the attractions of the ocean that it is enough for any place to stand on the shore. That one recommendation is sufficient. Down comes the Excursion Train with its thousands–some with a month’s range, others tethered to a six hours’ limit, but all rushing with one impulse to the water’s edge. Where are they to lodge? The old ‘town’ is perhaps half a mile inland, and turned as far away from sea as possible, for the fishermen who built it were by no means desirous of always looking at the sea or having the salt spray blowing in at their windows. They got as far back as they could, and nestled in the cliffs or behind the hill for the sake of shelter and repose. But this does not suit visitors whose eyes are always on the waves, and so a new town arises on the beach. Marine Terraces, Sea Villas, ‘Prospect Lodges’, ‘Bellevues’, hotels, baths, libraries and churches soon accumulate, till at length of the old borough is completely hidden and perhaps to be reached by an omnibus.
The story of this hypothetical village summarizes very well the core of Butler’s theory, according to which there are basically three different scenarios, as sketched in Figure 2a. In an unexploited area, the tourists are initially only a few people and their number grows very slowly (exploration). Following this discovery period, there is a phase of rapid growth, in general accompanied by a concomitant capital development, and, finally, a stagnation phase. After these phases, which are present in all cases, there are three main possible long-term scenarios:
- A.
- the tourists remain roughly constant at their maximum;
- B.
- after a decline, the tourism activities settle down to a plateau; or
- C.
- tourism activities dramatically decline.
Butler (1980) also envisioned two types of rejuvenation stage (i.e., the number of tourists increasing again following the stagnation phase): the first requires the addition of man-made attractions (such as Atlantic City’s gambling casinos), the second requires taking advantage of previously untapped natural resources (Butler cites some summer holiday villages that also cater to winter sports). In any case, as Butler clearly states, “it is almost certain that this [rejuvenation] stage will never be reached without a complete change in the attractions on which tourism is based.” Figure 2b shows that the model 3-5 can simulate the three scenarios, provided the parameters are suitably adjusted. This means that the model 3-5 is sufficiently flexible to adapt qualitatively to all relevant cases.
Butler's diagram is only a partial view of tourism dynamics, as it does not say anything about environmental quality and infrastructure. A full description of the tourism dynamics of a given site would require plotting either three time series, one for each component, or, alternatively, the line (trajectory) along which T, E, and C evolve in their three-dimensional space (state space). Figure 3 shows the trajectories corresponding to the three scenarios of Figure 2b: they all start close to point K on the E axis, because the initial conditions are characterized by an almost total absence of tourists and capital.
|
Fig. 3. Trajectories in state space corresponding to scenarios A, B, and C of Figure 2b.

|
The trajectories develop over time (as shown by the arrow) and tend for 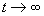 toward a point (equilibrium) in cases A and B, and toward a closed line (limit cycle) in case C. In the latter case, tourism activities periodically recover after long and dramatic declines. Situations where tourism activities recover after a severe decline have been observed and discussed by various authors (Christaller 1963, Plog 1973, Butler 1991). The fact that humans and their cultural practices can impact periodically on an ecosystem has also been remarked on in other contexts (Anderies 1998).
toward a point (equilibrium) in cases A and B, and toward a closed line (limit cycle) in case C. In the latter case, tourism activities periodically recover after long and dramatic declines. Situations where tourism activities recover after a severe decline have been observed and discussed by various authors (Christaller 1963, Plog 1973, Butler 1991). The fact that humans and their cultural practices can impact periodically on an ecosystem has also been remarked on in other contexts (Anderies 1998).
Equilibria and limit cycles are called attractors and represent the long-term behavior of the system. As such, they are the appropriate tool for discussing sustainability, which is, indeed, a long-term property of the system. In contrast, Butler's diagrams are not appropriate for discussing sustainable tourism, because they point out only the initial parts of the transition toward the attractors.
The aim of this section is to identify all long-term modes of behavior (i.e., the attractors) of the model 3-5 for different values of two parameters, namely investment rate, ε, and competition, a. Our analysis shows that the attractors of model 3-5 are either equilibria or limit cycles. Nevertheless, for parameter values in suitable ranges, the model can have two or three attractors. In such cases, each attractor has its own basin of attraction, which is the set of all initial states giving rise to trajectories tending toward the attractor. Thus, when there are multiple attractors, the initial conditions of the system play a crucial role because they determine the long-term behavior of the system.
Each point of the two-dimensional parameter space (ε,
a)
corresponds to a particular model of our family of models 3-5 and, therefore, to one specific set of attractors. If at least one of the two parameters is slightly perturbed, according to continuity, the position and form of the attractors will vary smoothly in state space (e.g., a limit cycle might become slightly bigger and faster), but all trajectories will remain qualitatively the same (e.g., an attracting cycle will remain an attracting cycle). Only at particular points in the parameter space will the above continuity argument fail. At these points, called bifurcation points (Kuznetsov 1995), small variations in the parameters entail significant changes in the model behavior. For example, an equilibrium
(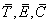 ) that is strictly positive, i.e.,
) that is strictly positive, i.e.,
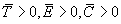 |
can be stable (i.e., attract all nearby trajectories) for a given parameter setting, but lose its stability if competition, a, is increased even by an infinitesimal amount. If this is the case, after variation in the parameter, the state of the system will not tend toward the equilibrium (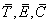 ) but toward another attractor. If this new attractor is infinitely close to the old one, the bifurcation is said to be non catastrophic. However, it is said to be catastrophic if a microscopic variation of the parameter gives rise to a macroscopic transition from one attractor to another. For example, this would be the case if a small increase in competition forced the system to switch from a strictly positive equilibrium
(
) but toward another attractor. If this new attractor is infinitely close to the old one, the bifurcation is said to be non catastrophic. However, it is said to be catastrophic if a microscopic variation of the parameter gives rise to a macroscopic transition from one attractor to another. For example, this would be the case if a small increase in competition forced the system to switch from a strictly positive equilibrium
(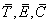 ) to an equilibrium
(
) to an equilibrium
(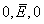 ) characterized by the absence of tourists and capital.
) characterized by the absence of tourists and capital.
Unions of bifurcation points are bifurcation curves that partition the parameter space (ε, a) into subregions. All models corresponding to the same subregion have qualitatively the same long-term behavior, because they have the same attractors. All bifurcation curves can be determined numerically using specialized software such as AUTO (Doedel and Kernévez 1986), LOCBIF (Khibnik et al. 1993), or CONTENT (Kuznetsov and Levitin 1997). Once a single bifurcation point in the parameter space is found, these packages automatically produce the entire bifurcation curve passing through that point. Readers interested in performing numerical bifurcation analysis of model (1-3) for various parameter settings can visit the AUTO site or download CONTENT.
Without going into further detail, we show the results of our analysis in Figure 4, for the parameter setting indicated in the caption. There are five bifurcation curves, denoted I, II, ..., V, that identify ten different regions, denoted 1, 2, ..., 10. The attractors of each region are also sketched in Figure 4 (readers skilled in bifurcation analysis will recognize that curves I, II, III, IV, and V are, respectively, a transcritical of equilibria, a fold of equilibria, a planar fold of equilibria, a Hopf, and a homoclinic bifurcation curve). In regions 1, 4, 8, and 10 the attractor is unique, but in the other regions, there are two or even three (region 7) alternative attractors. In these cases, the system is “fragile” because an accidental shock can suddenly perturb the state of the system and move it from being an attractor Ai into the basin of attraction of another attractor Aj. Thus, after the perturbation has ceased, the state of the system will tend toward the new attractor Aj and remain there until a new shock occurs. Another important point is that the strictly positive attractor is unique (when it exists). Moreover, in regions 3, 4, 6, and 7, the strictly positive attractor is a limit cycle. This means that, in these regions, the long-term behavior of the system can be characterized by recurrent ups and downs of the three state variables.
|
Fig. 4. Bifurcation diagram of model 3-5 in the parameter space (ε, a). Other parameter values are as in Figure 2b.

|
The parameters of the model can be subdivided into policy parameters and system parameters. Policy parameters identify the behavioral characteristics of agents and decision makers, and system parameters describe the other actors involved in the game, namely the environment, the tourists, and the alternative tourist sites. Therefore, a particular parameter setting can be viewed as a particular policy applied to a particular system. In order to judge the economic impact of a policy on a given destination area, we should be able to associate a value judgment concerning the tourism industry to each parameter setting. The wisest choice is to associate a zero-one value judgment (i.e., “bad” or “good”) to each parameter setting. This is what has been done during the last decade, with the introduction of various notions of sustainability (Ludwig et al. 1993, Bramwell and Lane 1993). Many of these notions refer to extreme compromise solutions between economic development and environmental protection. For many economists, sustainability means guaranteed economic growth under the weak constraint of no irreversible damage to the environment (Goodland and Ledec 1987, Solow 1991, Turner 1993, Beltratti 1997). Conversely, for environmentalists, sustainability is simply viewed as no further deterioration of the environment resulting from the use of natural resources (Rubenstein 1993). Our definition of sustainability (see below), however, gives equal emphasis to economic and environmental aspects, as supported by various authors (Bender et al. 1994, Gatto 1995, Wall 1997).
Let us qualify the economic impact of a policy applied to a given site by saying that the policy is profitable if it can sustain the tourism industry indefinitely. In the economic literature, this aspect is usually dealt with through maximization of discounted utility (Beltratti 1997, Cheve 2000). Here we follow a simpler approach: we say that a policy is profitable if at least one of the associated attractors is characterized by T(t) > 0 for all t (notice that this implies C(t) > 0 for all t). The property T(t) > 0 is a structural property of the attractors, as can be verified from Figure 4. From the same figure, it follows that only region 8 corresponds to non-profitable policies. Indeed, in all other regions, at least one attractor is characterized by a permanent tourist activity. There is, nevertheless, an important difference between these regions. In fact, in some of them, there are also attractors characterized by the absence of the tourism industry (i.e., T(t) = 0). In such cases, we say that the policy is profitable but risky, because an unexpected accidental shock, like a war, an epidemic, or an episode of xenophobia, can perturb the state of the system and cause a transient ending to an attractor characterized by no tourism industry. Regions 2, 3, 7, and 9 of Figure 4 correspond to profitable but risky policies, while all regions below curve I are profitable and safe. Thus, if competition is sufficiently low, all policies are profitable and safe, but if competition is sufficiently high, all policies are non-profitable, a quite reasonable result.
Following a similar line of reasoning for judging the environmental impact of a policy in a given area, we can say that a policy is compatible when it avoids complete degradation of the environment. In purely mathematical terms, this means that at least one of the associated attractors has E(t) > 0 for all t. From this definition, it follows that only region 10 in Figure 4 is not compatible. Again, we can distinguish between safe and risky policies and we find that all regions above curve III correspond to safe, compatible policies.
Finally, in line with the theory of conflict resolution in multiobjective analysis (Keeney and Raiffa 1976) and in accordance with some of the most recent ideas on sustainability (Ecological Society of America 1993), we say that a policy is sustainable if it offers a chance of maintaining the tourism industry indefinitely without jeopardizing the environment. Thus, a policy is sustainable when one of its associated attractors is characterized by E(t) > 0 and T(t) > 0 (and hence C(t) > 0 ) for all t, i.e., when one of its attractors is strictly positive. As already stated, this definition is not as partisan as those proposed by economists, who pretend that
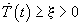 or environmentalists, who pretend that
or environmentalists, who pretend that
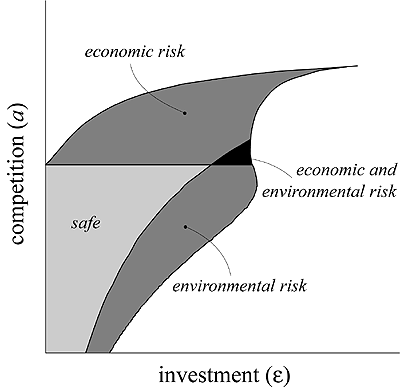
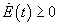 . Obviously, a sustainable policy is profitable and compatible, but the converse is not true, as can easily be seen by looking at the attractors in region 9 of Figure 4. Of course, a sustainable policy can be safe (and is certainly such if the attractor is unique). But it can also be risky for the environment and/or for the economy. Following these definitions, we can easily derive the region of sustainable policies from Figure 4 and subdivide it, as shown in Figure 5, into a region of safe policies and various regions of risky policies. Such a diagram, hereafter called a sustainability diagram, shows that the region of sustainable policies is bounded. Moreover, it can be shown that the two bifurcation curves delimiting the sustainability region are catastrophic. This means that any parameter variation implying the loss of sustainability will be accompanied by a catastrophic collapse of the environment and/or the tourism industry. In contrast, the subregion of sustainable and safe policies is delimited by two bifurcation curves that are non-catastrophic for the strictly positive attractor. Such a region is rather small and is characterized by low competition and investment rate. As soon as competition becomes too strong, the policy becomes risky for the economy, and if local agents are too greedy, the policy is risky for the environment.
. Obviously, a sustainable policy is profitable and compatible, but the converse is not true, as can easily be seen by looking at the attractors in region 9 of Figure 4. Of course, a sustainable policy can be safe (and is certainly such if the attractor is unique). But it can also be risky for the environment and/or for the economy. Following these definitions, we can easily derive the region of sustainable policies from Figure 4 and subdivide it, as shown in Figure 5, into a region of safe policies and various regions of risky policies. Such a diagram, hereafter called a sustainability diagram, shows that the region of sustainable policies is bounded. Moreover, it can be shown that the two bifurcation curves delimiting the sustainability region are catastrophic. This means that any parameter variation implying the loss of sustainability will be accompanied by a catastrophic collapse of the environment and/or the tourism industry. In contrast, the subregion of sustainable and safe policies is delimited by two bifurcation curves that are non-catastrophic for the strictly positive attractor. Such a region is rather small and is characterized by low competition and investment rate. As soon as competition becomes too strong, the policy becomes risky for the economy, and if local agents are too greedy, the policy is risky for the environment.
|
Fig. 5. Sustainability diagram of model 3-5 with respect to investment and competition. Parameter values as in Figure 2b.
|
The analysis described in Figs. 3 and 4 concerning the effects of competition and investment, has been repeated for other pairs of parameters in order to obtain a better understanding of the problem. The results are shown in Figure 6, where four different sustainability diagrams are reported. In all diagrams, on the horizontal axis we have a policy parameter, like price, environmental reclamation, or investment, and on the vertical axis, there is a system parameter describing the attractiveness of alternative sites (competition) or some behavioral characteristics of the tourists, such as their appreciation of the facilities (μ
C in Eq. 1) and their ability to perceive the quality of the environment (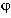 E in Eq. 1). In all cases, the boundary of the sustainable region is composed of two catastrophic bifurcation curves.
E in Eq. 1). In all cases, the boundary of the sustainable region is composed of two catastrophic bifurcation curves.
Safe policies are “surrounded” by risky policies, and a continuous increase in the system parameter transforms a safe sustainable policy first into a risky sustainable policy and then into an unsustainable policy. In general, sustainability requires low prices, low investments, and high environmental reclamation.
Another property that is often mentioned in the context of sustainability is adaptivity (Holling 1986, Walters 1986, Holling 1993). It corresponds to the possibility of changing policy parameters, on the basis of perceived variations in system parameters, in such a way that sustainability can still be guaranteed. A typical question that agents must be able to answer is, for example, the following: if competition increases slowly but continuously, should the policy also be varied in order to avoid, or at least delay, negative consequences? A question like this can be answered qualitatively by looking once more at our sustainability diagrams. In this specific case, we should look at Figs. 4, 5a, and 5b which have, on the vertical axis, the system parameter “competition” and, on the horizontal axis, a policy parameter. Thus, if competition increases and the policy remains unchanged, the consequences can be detected by looking at what happens by moving up vertically in each diagram. The three figures show that a safe sustainable policy will first become economically risky and finally unsustainable, so that the problem of avoiding these consequences through adaptation is a well posed one. Figure 5 indicates that varying the investment rate will not avoid or delay the time at which the policy becomes risky, because the upper boundary of the safe region is horizontal. The same is true in Figure 6b, but Figure 6a shows that the policy can adapt to increasing competition and remain safe, at least for a longer time, if prices are slowly decreased. Thus, in conclusion, if the aim is to avoid economically risky situations, price control seems to be the proper action to take to cope with increasing competition. In contrast, if risk is accepted and the target is to avoid or delay the time at which the policy becomes unsustainable, all three policy parameters are good control candidates for achieving the task, and the diagrams suggest increasing investment rate and environmental reclamation, and decreasing prices. In practice, it might be rather hard to find the right mix of control actions; we can see from the diagrams that exaggerated reactions could actually generate an environmental crash rather than simply avoid an economic crash. Moreover, when many system parameters vary at the same time, it becomes more difficult to adapt the policy, because some of the sustainability diagrams may suggest conflicting actions. For example, if appreciation for facilities also increases (as it does nowadays), Figure 6c suggests increasing prices to maintain safe conditions, but Figure 6a suggests just the opposite for coping with increasing competition.
The problem of sustainable tourism has been dealt with theoretically in this paper using a minimal model with three state variables: tourists, environment, and capital. Although simplistic, this paper is of value for three reasons.
First, it introduces the approach of minimal descriptive models in the context of tourism, which has been traditionally dominated by the use of detailed simulation models. In other science fields, such as epidemiology (Ross 1909), plant and animal ecology (Volterra 1926), renewable resources management (Clark 1976), and economics (Forrester 1961, Brock and Malliaris 1989), this happened long ago and the approach is now appreciated and well established. Indeed, minimal (stylized) models have recently been used to discuss the role of human actors in ecological–economic systems (Anderies 2000).
Second, the specific results are quite interesting. We have, in fact, shown that sustainable tourism can be achieved, provided agents are prudent about reinvesting their profits and are inclined to protect the environment. We have also seen that sustainability is very often at risk, because accidental shocks can easily trigger a switch from a profitable and compatible behavior to an unprofitable or incompatible one. Moreover, adaptation of sustainable policies is also possible, but is very difficult to achieve in practice, and can at best delay the occurrence of a catastrophe but not avoid it, if competition among tourist sites continues to grow. All these results agree with conventional wisdom and observations, but the interesting thing here is that they are theoretically derived from a few very simple, abstract premises.
Finally, the third reason does not relate strictly to the problem of tourism, but rather to the general topic of sustainability. Here, we base the notions of profitability, compatibility, and sustainability, which are more and more pervasive in the field of resource management, on structural properties of the attractors of a dynamic system. In a similar fashion to what has been done for resilience by Ludwig et al. (1997), this creates an important and promising bridge between sustainability and bifurcation theory, one of the most important areas in systems theory.
The weaknesses of the paper are the typical weaknesses of minimal models. First of all, the three components used in the model cannot cover the social, cultural, and political aspects involved in tourism development. This means that our conclusions should not be applied to those cases in which such aspects are dominant. For example, a fourth variable, namely local labor population, should be added to the model if the social implications of tourism development are to be discussed. Moreover, the three components are too aggregated. For example, a more detailed description of the tourist population is needed. Indeed, different tourists have different cultures and can be described by Eq. 3 with different parameter values. Our analysis shows (see for example Figs. 5c and 5d) that the behavior of the system can be radically different if tourists are different, to the point that, in some cases, tourism cannot persist. On the other hand, we know that a tourist site is rarely abandoned by tourists but is more likely visited by tourists of lower and lower classes (Butler 1980). This fact can be studied through a slightly extended minimal model with two or three different classes of tourists acting as competing exploiters of the same resource, thus obeying the principle of competitive exclusion (Hardin 1960). In a similar way, we can substitute Eq. 5, describing capital, with two similar equations having different parameter values in order to study the case of diversified investments for infrastructure and facilities. But even without modifying the present aggregation level, some of the assumptions encapsulated in the minimal model can be relaxed in order to study other cases of interest. For example, we could try to see if the introduction of suitable investment constraints, based on environmental quality and/or services, has the power to amplify the class of sustainable policies.
Responses to this article are invited. If accepted for publication, your response will be hyperlinked to the article. To submit a comment, follow this link. To read comments already accepted, follow this link.
This work is dedicated to Gin Racheli who devoted so much of her energy to studying the culture of minor Italian islands and to understanding and living with the “people of sea.” The paper was written at the International Institute for Applied Systems Analysis, Laxenburg, Austria. The study was financially supported by the Fondazione Eni Enrico Mattei, (FEEM), by the Consiglio Nazionale delle Ricerche, Project ST/74, “Mathematical methods and models for the study of biological phenomena” and by a prize from Italgas to R.C. The authors are grateful to Dr. Alessandro Lanza, who first suggested the problem and gave important advice and to Dr. David Munro (Director of the Royal Scottish Geographical Society for making available to us a reprint of Gilbert's paper. Dr. Stephen Carpenter and a series of anonymous reviewers are also acknowledged for helping the authors clarify a number of important points.
Agarwal, S. 1997. The resort cycle and seaside tourism: an assessment of its applicability and validity. Tourism Management 18:65-73.
Akis, S. 1998. A compact econometric model of tourism demand for Turkey. Tourism Management 19:99-102.
Akis, S., N. Peristianis, and J. Warner. 1996. Residents' attitudes to tourism development: the case of Cyprus. Tourism Management 17:481-494.
Anderies, J. M. 1998. Culture and human agro-ecosystem dynamics: the Tsembaga of New Guinea. Journal of Theoretical Biology 192:515-530.
Anderies, J. M. 2000. On modelling human behavior and institutions in simple ecological economic systems. Ecological Economics 35:393-412.
Arrow, K., B. Bolin, R. Costanza, P. Dasgupta, C. Folke, C. S. Holling, B. Jansson, S. Levin, K. Mäler, C. Perrings, and D. Pimental. 1995. Economic growth, carrying capacity and the environment. Science 268:520-521.
Beltratti, A. 1997. Growth with natural and environmental resources. Pages 7-42 in C. Carraro and D. Siniscalco, editors. New directions in the economic theory of the environment. Cambridge University Press, Cambridge, UK.
Bender, M. J., G. V. Johnson, and S. P. Simonovic. 1994. Sustainable management of renewable resources: a comparison of alternative decision approach. International Journal of Sustainable Development 1:77-88.
Brock, W. A., and A. G. Malliaris. 1989. Differential equations, stability and chaos in dynamic economics. North-Holland, Amsterdam, The Netherlands.
Brown, K., R. K. Turner, H. Hameed, and I. Bateman. 1996. Tourism and sustainability in environmentally fragile areas: case studies from the development and cultural theory. The International Journal of Sustainable Development and World Ecology 3:1-14.
Bramwell, B., and B. Lane. 1993. Sustainable tourism: an evolving global approach. Journal of Sustainable Tourism 1:6-16.
Butler, R. W. 1980. The concept of a tourist area cycle of evolution: implications for management of resources. Canadian Geographer 24:5-12.
Butler, R. W. 1991. Tourism, environment, and sustainable development. Environmental Conservation 18:201-209.
Carpenter, S., W. Brock, and P. Hanson. 1999a. Ecological and social dynamics in simple models of ecosystem management. Conservation Ecology 3(2):4. [Online, URL: http://www.consecol.org/vol3/iss2/art4].
Carpenter, S. R., D. Ludwig, and W. A. Brock. 1999b. Management of eutrophication irreversible change. Ecological Applications 9:751-771.
Cheve, M. 2000. Irreversibility of pollution accumulation. Environmental and Resource Economics 16:93-104.
Christaller, W. 1963. Some considerations of tourism location in Europe: the peripheral regions—underdeveloped countries—recreation areas. Papers of the Regional Science Associations 12:95-105.
Clark, C. W. 1976. Mathematical bioeconomics: the optimal management of renewable resources. John Wiley & Sons, New York, New York, USA.
Coccossis, H., and P. Nijkamp, editors. 1995. Sustainable Tourism Development. Avebury, Aldershot, UK.
Dahles, H., and K. Bras. 1999. Entrepreneurs in romance—Tourism in Indonesia. Annals of Tourism Research 26:267-293.
Dharmaratne, G. S. 1995. Forecasting tourist arrivals in Barbados. Annals of Tourism Research 22:804-818.
Doedel, E. J., and J. P. Kernévez. 1986. AUTO: Software for continuation and bifurcation problems in ordinary differential equations. Applied Mathematics Report. California Institute of Technology, Reading, Massachusetts, USA.
Douglas, N. 1997. Applying the life cycle model to Melanesia. Annals of Tourism Research 24:1-22.
Ecological Society of America. 1993. Forum on “Science and Sustainability,”. Ecological Applications 3:545-589.
Forrester, J. W. 1961. Industrial Dynamics. MIT Press, Cambridge, Massachusetts, USA.
Gatto, M. 1995. Sustainability: is it a well defined concept? Ecological Applications 5:1181-1183.
Gatto, M., L. Ghezzi, and S. Rinaldi. 1991. Optimal investment in the reclamation of eutrophic water bodies. Journal of Optimization Theory and Applications 71:389-398.
Gilbert, E. W. 1939. The growth of inland and seaside health resorts in England. Scottish Geographical Magazine 55:16-35.
Goodland, R., and G. Ledec. 1987. Neoclassical economics and principles of sustainable development. Ecological Modelling 38:19-46.
Hardin, G. 1960. The competitive exclusion principle. Science 131:1292-1298.
Harrison, D. 1995. Development of tourism in Swaziland. Annals of Tourism Research 22:135-156.
Herfindahl, O. C., and A. V. Kneese. 1974. Economic Theory of Natural Resources. Merrill Publishing Company, Columbus, Ohio, USA.
Holling, C. S. 1986. The resilience of terrestrial ecosystems: local surprise and global change. Pages 292-317 in W. C. Clark and R. E. Munn, editors. Sustainable development of the biosphere. Cambridge University Press, Cambridge, UK.
Holling, C. S. 1993. Investing in research for sustainability. Ecological Applications 3:552-555.
Keeney, R. L., and H. Raiffa. 1976. Decisions with Multiple Objectives: Preferences and Value Tradeoffs. Wiley, New York, New York, USA.
Khibnik, A. I., Y. A. Kuznetsov, V. V. Levitin, and E. V. Nikolaev. 1993. Continuation techniques and interactive software for bifurcation analysis of ODEs and iterated maps. Physica D 62:360-371.
Kulendran, N., and M. L. King. 1997. Forecasting international quarterly tourist flows using error-correction and time-series models. International Journal of Forecasting 13:319-327.
Kulendran, N., and Witt, S. F. 2001. Cointegration versus least squares regression. Annals of Tourism Research 28:291-311.
Kuznetsov, Y. A. 1995. Elements of Applied Bifurcation Theory. Springer Verlag, New York, New York, USA.
Kuznetsov, Y. A., and V. V. Levitin. 1997. CONTENT: A Multiplatform Environment for Continuation and Bifurcation Analysis of Dynamical Systems. Centrum voor Wiskunde en Informatica, Kruislaan 413, 1098 SJ Amsterdam, The Netherlands.
Lim, C. 1997. Review of international tourism demand models. Annals of Tourism Research. 24:835-849.
Lindberg, K., editor. 1991. Policies for Maximizing Nature Tourism's Ecological and Economic Benefits. World Resources Institute, Washington, DC, USA.
Ludwig, D. 1993. Environmental sustainability: magic, science, and religion in natural resource management. Ecological Applications 3:555-558.
Ludwig, D., R. Hilborn, and C. Walters. 1993. Uncertainty, resource exploitation, and conservation: lessons from history. Science 260:17-36.
Morley, C. L. 1998. A dynamic international demand model. Annals of Tourism Research 25:70-84.
O'Hare, G., and H. Barrett. 1997. The destination life cycle: international tourism in Peru. Scottish Geographical Magazine 113:66-73.
Plog, S. C. 1973. Why destination areas rise and fall in popularity. Cornell Hotel and Restaurant Association Quarterly 13:6-13.
Rinaldi, S., W. C. Sanderson, and A. Gragnani. 1996. Pollution control policies and natural resources dynamics: a theoretical analysis. Journal of Environmental Management 48:357-373.
Roe, E. M. 1996. Sustainable development Journal of Sustainable Development and World Ecology 3:1-14.
Ross, R. 1909. The Prevention of Malaria. Murray, London, UK.
Rubenstein, D. I. 1993. Science and the pursuit of a sustainable world. Ecological Applications 3:585-587.
Seddighi, H. R., and D. F. Shearing. 1997. The demand for tourism in North East England with special reference to Northumbria: an empirical analysis. Tourism Management 18:499-511.
Shah, A. 1995. The Economics of Third World National Parks. Edward Elgar Publishing, Aldershot, UK.
Smith, V. L., and W. R. Eadington, editors. 1992. Tourism Alternatives: Potential and Problems in the Development of Tourism. University of Pennsylvania Press, Philadelphia, Pennsylvania, USA.
Solow, R. M. 1991. Sustainability: an Economist's Perspective. Marine Policy Center, Woods Hole Oceanogravarphic Institution, Massachusetts, USA.
Turner, R. K. 1993. Sustainability: principles and practice. Pages 3-36 in R. K. Turner, editor. Sustainable environmental economics and management. Belhaven, London, UK.
Volterra, V. 1926. Variazioni e fluttuazioni del numero d'individui in specie animali conviventi. Memorie dell'Accademia dei Lincei 6:31-113.
Wall, G. 1997. Is ecotourism sustainable? Environmental Management 21:83-491.
Walker, P. A., R. Reiner, D. McDonald, and V. Lyne. 1998. The Tourism Futures Simulator: a systems thinking approach. Environmental Modelling & Software 14:59-67.
Walters, C. J. 1986. Adaptive Management of Renewable Resources. McGraw Hill, New York, New York, USA.
Williams, A. M., and G. Shaw, editors. 1988. Tourism and Economic Development: Western European Experiences. Belhaven, London, UK.
Witt, S. F., and C. A. Witt. 1995. Forecasting tourism demand: A review of empirical research. International Journal of Forecasting 11:447-475.
Address of Correspondent:
Renato Casagrandi
Dipartimento di Elettronica e Informazione
Politecnico di Milano,
Via Ponzio, 34/5
20133, Milano, Italy.
http://www.elet.polimi.it/people/casagran
Phone: +39-02-23993471
Fax: +39-02-23993412
casagran@elet.polimi.it
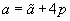 and
and  . The darkest regions correspond to sustainable policies that are both risky for the economy and for the environment. In (a) the component ã is on the vertical axis. In (b) ε=0.6. In (c) ã =2. In (d) a=6. All other parameters are as in Figure 2b.
. The darkest regions correspond to sustainable policies that are both risky for the economy and for the environment. In (a) the component ã is on the vertical axis. In (b) ε=0.6. In (c) ã =2. In (d) a=6. All other parameters are as in Figure 2b.
