Spatial Modeling of Risk in Natural Resource Management

Peter G. Jones¹ and Philip K. Thornton²

• Abstract
• Introduction
• Methods
  • CERES-Maize
  • MarkSim and weather data
  • Soils data
  • Genetic coefficient data and management data
  • Climate change models
  • Coherence clustering and modification of MarkSim
  • Simulations
• Results
  • Weather coherence
  • Maize and pasture performance
• Conclusions
• Responses to this Article
• Acknowledgments
• Literature Cited

Making decisions in natural resource management involves an understanding of the risk and uncertainty of the outcomes, such as crop failure or cattle starvation, and of the normal spread of the expected production. Hedging against poor outcomes often means lack of investment and slow adoption of new methods. At the household level, production instability can have serious effects on income and food security. At the national level, it can have social and economic impacts that may affect all sectors of society. Crop models such as CERES-Maize are excellent tools for assessing weather-related production variability. WATBAL is a water balance model that can provide robust estimates of the potential growing days for a pasture. These models require large quantities of daily weather data that are rarely available. MarkSim is an application for generating synthetic daily weather files by estimating the third-order Markov model parameters from interpolated climate surfaces. The models can then be run for each distinct point on the map. This paper examines the growth of maize and pasture in dryland agriculture in southern Africa. Weather simulators produce independent estimates for each point on the map; however, we know that a spatial coherence of weather exists. We investigated a method of incorporating spatial coherence into MarkSim and show that it increases the variance of production. This means that all of the farmers in a coherent area share poor yields, with important consequences for food security, markets, transport, and shared grazing lands. The long-term aspects of risk are associated with global climate change. We used the results of a Global Circulation Model to extrapolate to the year 2055. We found that low maize yields would become more likely in the marginal areas, whereas they may actually increase in some areas. The same trend was found with pasture growth. We outline areas where further work is required before these tools and methods can address natural resource management problems in a comprehensive manner at local community and policy levels.

KEY WORDS: crop modeling, dryland agriculture, global change, Global Circulation Model, maize, Markov models, MarkSim, natural resource management, risk, southern Africa, spatial modeling, weather simulation.

Published: January 10, 2002

Agriculture is full of risk and uncertainty. Risk has been cited as contributing to slowed technology diffusion, fragmentation of landholdings, and price instability (Walker and Ryan 1990). It has a profound influence on decisions because it may strongly modify choices from among a set of alternatives. At the household level, risk and uncertainty can lead to substantial production instability with flow-on effects on income levels and food security. At the national level, agricultural production instability can have enormous social and economic impacts affecting all sectors of society. These factors influence decisions taken in agricultural production that directly affect the economic feasibility of resource management options.

Many methods and tools have been developed to try to deal with or minimize risk. Crop simulation models, for example, are excellent tools for assessing the weather-related production variability associated with particular strategies for the management of agricultural enterprises and natural resources. Simulation results can be used in a wide variety of other analytical frameworks, such as economic surplus and mathematical programming models, to provide information to a range of decision makers (Thornton and Wilkens 1998, Thornton and Herrero 2001).

Traditionally, point models such as CERES-Maize have been run on long data sets of daily weather available from existing or historical meteorological stations. Stochastic weather simulation is often used to augment the data where historical runs are not long enough (Richardson 1985, Jones and Thornton 1993, 1997). The results from runs on such data may be used to interpolate and map characteristics of the model output. However, the modeled processes are intrinsically nonlinear and this approach is fraught with difficulties. It would be better to map the modeled response by running the model for each point on the map. This is now feasible using MarkSim (Jones and Thornton 1999, 2000). MarkSim is an application available on CD-ROM that will generate synthetic daily weather files for use with models such as CERES-Maize. The model can be run for each distinct point on the map by estimating the third-order Markov model parameters from interpolated climate surfaces. The relevant characteristics can be extracted from each model run and can be readily mapped in the study area.

A characteristic of this approach is that each point is evaluated in isolation. However, the realism of a general crop failure is never simulated. Off-site effects of the stochasticity of climate are largely underestimated; in the real world when you have a shortage of domestic food or cattle feed, your neighbors are usually similarly affected. When a harvest is good, the market price plummets. This has real implications for national and regional infrastructure, communications, and resource management on a broad scale.

For the study, we chose a window in southern Africa extending from 22º E to 42º E and from 23º S to 5º S, covering an area of about 38,000 km². This window covers the southern part of Tanzania, Malawi, much of Mozambique, and all of Zimbabwe, and extends west from the Indian Ocean to include Zambia, the southeastern part of the Democratic Republic of Congo (DRC), and small portions of Angola (Fig. 1). We chose this area because of its overall single, well-defined growing season and the considerable spatial variability in total annual rainfall. The following subsections briefly describe the models, databases, and methods that enable us to generate various maize and pasture risk scenarios for this region.

Fig. 1. The study area in southern Africa, 22° E to 42° E, 3° S to 23° S (the southern part of Tanzania, Malawi, much of Mozambique, and all of Zimbabwe, extending west from the Indian Ocean to include Zambia, southeastern Democratic Republic of Congo (DRC), and small portions of Angola). Letters in yellow denote sample points, as in Fig. 3.

CERES-Maize

CERES-Maize is a model that simulates the growth, development, and yield of the maize crop. It was designed to use a minimum set of soil, weather, genetic, and management information. The model is run with a daily time step and requires daily weather data (maximum and minimum temperature, solar radiation, and rainfall). It calculates crop phasic and morphological development using temperature, day length, and genetic characteristics. Leaf area index, plant population, and row width provide information for determining the amount of light interception, which is assumed to be proportional to biomass production. A water and nitrogen balance submodel provides feedback that influences the development of growth processes (Ritchie et al. 1998). CERES-Maize has been widely used in North America and in the tropics and subtropics (Tsuji et al. 1998). The model has also been successfully validated and applied at many sites in our study window (see, e.g., Muchena and Iglesias [1995] for Zimbabwe, Thornton et al. [1995] for Malawi, and Schulze [2000] and Durand and du Toit [2000] for southern Africa). To run CERES-Maize, we need data on daily weather, the soil profile, genetic coefficients for the variety simulated, and information on the crop management.

MarkSim and weather data

Over the last few years, we have developed and extensively tested a third-order Markov rainfall model (Jones and Thornton 1993). Being able to model outlying rainfall years satisfactorily is particularly important in studies aimed at quantifying production system risk. A Markov model works by randomly sampling a series of events where the probability of observing an event depends on the occurrence of previous events. A third-order Markov model takes into account events occurring over the previous three days. We have found that, whereas a lower order model is often sufficient for temperate climates, the third order is necessary for many tropical climates. This simple model should be able to simulate the variance of monthly and annual rainfall for sites in the tropics and subtropics, but even the third-order model falls short of reality. The MarkSim rainfall generator makes good this deficit by means of annual random resampling of certain of the model’s own parameters.

Jones and Thornton (1997) showed that patterns could be discerned in the parameter values that were typical for certain types of climate. The model can thus be used to interpolate rainfall data for places where they do not exist. Regression models were developed that predict the Markov model parameters within certain restricted climate sets (Jones and Thornton 1999). The MarkSim system identifies the climate set relevant to any required point on the globe, using interpolated climate surfaces, and evaluates the model parameters for that point. The climate surfaces used are the 10 minutes-of-arc surfaces fitted at Centro Internacional de Agricultura Tropical (CIAT), based on the National Oceanographic and Atmospheric Administration (NOAA) dataset TGOP006 (NOAA 1984), using inverse square distance weights for spatial interpolation, and a standard lapse rate model to correct temperature for elevation effects. These surfaces are based on historical data from stations having more than 10 years of record taken from the period 1920–1990. Therefore, they are not standard climate normals, but compensate for the lack of time standardization by including more stations. Jones and Thornton (2000) describe the program in detail. Hartkamp et al. (1999) have shown that inverse distance weighting methods perform as well as thin-plate smoothing and co-kriging. A wide range of statistical validation tests of the MarkSim simulated data has been presented in Jones and Thornton (1993, 1997, 1999, 2000).

Soils data

We used the Food and Agriculture Organization digital soil map of the world (FAO 1974, 1995) and cut out the appropriate window (see Fig. 1). For all of the soil types in the window, we made a qualitative assessment (based on the soil unit ratings in FAO [1978]) as to their agricultural suitability for maize production: class 1, unsuitable; class 2, moderately suitable; and class 3, highly suitable. We then assembled representative profiles from the International Soils Reference and Information Center’s World Inventory of Soil Emission Potentials (WISE) database (Batjes and Bridges 1994, Batjes 1995) for each of the soils in the FAO soil map units that fell into classes 2 and 3. We used a combination of the pedotransfer functions in the decision support system for agricultural technology transfer, implemented in a VisualBasic program by Ravic Nijbroek at International Livestock Research Institute (ILRI), and a database at CIAT, assembled by Jamie Fairbairn (unpublished data) to estimate water-holding capacities.

Genetic coefficient data and management data

We used Katumani Composite B (KCB), a Kenyan, open-pollinated maize variety developed >25 years ago as a fairly short-season variety (about 120 days) for the dry mid-altitude conditions of Kenya (Hassan 1998). It was planted at a density of 3.7 plants/m², with 50 kg/ha of mineral N distributed through the soil profile. For all soils, 10 kg/ha of inorganic N was applied to the crop at planting. Planting was carried out automatically, when the first 30 cm of the soil profile first reaches 40% field moisture capacity each season. The genetic coefficients for KCB were determined in growth experiments carried out in the Republic of South Africa (A. S. du Toit, personal communication 1999).

Climate change models

To derive a set of climate surfaces for Africa for the middle of 2041–2070, we accessed the Intergovernmental Panel on Climate Change (IPCC) Data Distribution Centre on the worldwide web (URL: http://ipcc-ddc.cru.uea.ac.uk/). We decided to use a recent experiment conducted at the Hadley Centre, East Anglia, using the new Unified Model (Cullen 1993). The model, HadCM2, has a spatial resolution of 2.5° x 3.75° (latitude by longitude). This produces a surface spatial resolution of about 417 km x 278 km at the equator. In order to undertake a “warm-start” experiment, the model must be perturbed with a forcing from an early historical era when the radiative forcing was relatively small compared with the present. The experiment performed with HadCM2 started with forcing from the middle industrial era, around1860 (Mitchell et al. 1995, Johns et al. 1997). We used the monthly mean values of maximum and minimum temperature and precipitation for the period 2041–2070. In the following analyses, we refer to these as the 2055 data. We used the standard CIAT technique of inverse square distance weighted interpolation on the GCM model results to interpolate to the same grid as MarkSim (Jones and Thornton 2000)

Coherence clustering and modification of MarkSim

The spatial coherence and variability of weather are manifest at a wide range of scales. On a daily basis, it is not unusual to have rain on one farm while the neighbors’ fields are dry. A county, watershed, or market hinterland may be subject to water restrictions, while another area of the country experiences good rains. Events such as ENSO (El Niño-Southern Oscillation) may produce widespread drought in large areas, whereas other areas are subject to flooding.

The pixel-by-pixel simulation of MarkSim produces realistic results in the first case. Local variation in weather is built into the basic stochastic process. We conjecture that the mid-scale regional coherence may be approached via the resampling of the Markov probability parameters, but this remains to be tested thoroughly. If these change in lock step across a region, the resultant weather patterns will show a marked regional coherence imposed on the basic Markov process. Global forcing events, such as ENSO, are not yet incorporated in MarkSim, but we will be looking at this possibility soon.

In this study, we have concentrated on the mid-range spatial coherence of climate. We used the MarkSim cluster algorithm to group the climates of the study window (23,760 pixels). This was a leader cluster algorithm with a second pass to reallocate pixels to the closest cluster seed using the normalized monthly rainfall, temperature, and diurnal temperature range as the 36 cluster variates. Rainfall was transformed to the square root before normalization. We made one run from cluster to a few large climate regions, and a second to produce more, but smaller, areas. After cleaning to eliminate areas with less than six pixels, we obtained 21 areas in the first case and 51 in the second.

We modified MarkSim to separate the random number series for the parameter resampling from the basic Markov process and the gamma distribution sampling of rainfall event size. In each case, we constructed a common set of random normal deviates that were used to coordinate the random resampling throughout each climate zone.

Simulations

Figure 2 shows the links between the various databases and tools that were previously described. We ran six experiments or scenarios. These involved 3975 treatments (unique combinations of soil and weather inputs for the 1042 sample points; note that there may be 1–6 soil types per pixel) of CERES-Maize. Each treatment was replicated 29 times (making use of 30 years of simulated weather, because the maize growing season usually crossed years). The six experiments were:

Fig. 2. Schema of steps and methods in the analysis.

1. Markov weather parameters using current long-term climate (“present weather”) assuming complete independence between weather grid cells (“random weather”).
2. Weather parameters using current long-term climate, but with weather dependence across 21 zones as described earlier.
3. Weather parameters using current long-term climate, but with weather dependence across 51 zones.
4. Weather parameters using estimated long-term climate for the period 2041–2070 (“2055 weather”), assuming complete independence between weather grid cells.
5. Weather parameters using 2055 long-term climate, but with weather dependence across 21 zones.
6. Weather parameters using 2055 long-term climate, but with weather dependence across 51 zones.

The 115,275 runs for each scenario took about 6 h on a Pentium III processor. The model WATBAL was run for the same set of scenarios to give an indication of pasture growth for the same sample points. As a proxy for this, we used the number of growing days, defined as the number of days when the ratio of actual to potential evapotranspiration exceeded 0.5. Because it is a much simpler model than CERES, it ran more quickly. Input and analysis programs were custom-written in FORTRAN, and maps were generated using IDRISI (Eastman 1993).

Our discussion of the results is limited to considering the impact of rainfall coherence and to comparing maize and pasture yields using current weather patterns and the 2055 scenario patterns.

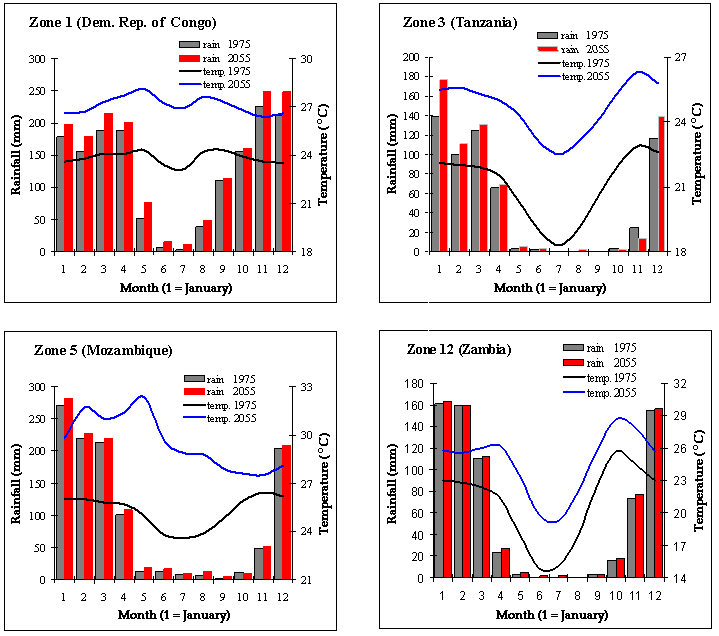
To give an idea of the types of climate in the study window, Fig. 3 shows monthly rainfall and temperatures for four sites in four of the 21 zones, for current conditions and those simulated (using the Hadley GCM) to occur using in 2055. The four sites are:

Fig. 3. Monthly rainfall and temperatures representative of present and simulated 2055 climates for a random site in: zone 1 in the Democratic Republic of the Congo; zone 5 in Mozambique; zone 3 in Tanzania; and zone 12 in Zambia. See Fig. 1 for locations.

    DRC: 6.58 º S, 23.50 º E, elevation 761 m

    Tanzania: 6.25 º S, 34.33 º E, elevation 1356 m

    Mozambique: 12.91 º S, 39.50 º E, elevation 426 m

    Zambia: 16.91 º S, 24.33 º E, elevation 1066 m

Even for these four sites (see Fig. 3), although temperature increases in all months, the amounts and patterns of increase simulated to occur with the GCM show distinct differences. For most months in this sample, rainfall would appear to increase slightly, but this is offset by the increasing temperature.

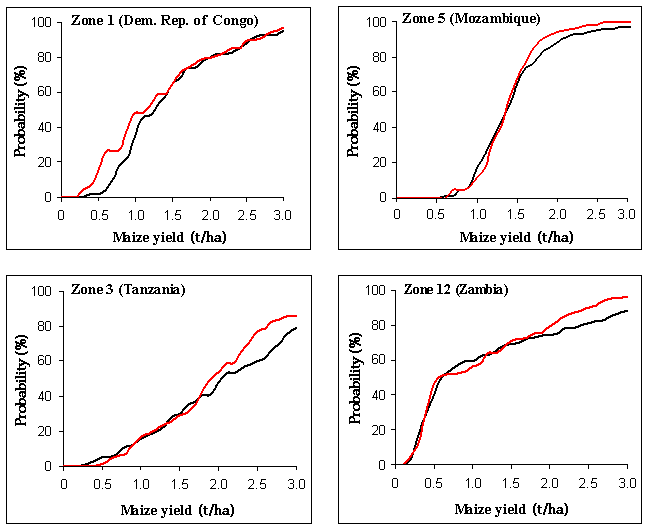
Thus, the way in which changing rainfall patterns may interact with generally increased temperatures to affect agricultural production depends on location. Fig. 4 shows cumulative probability functions for simulated maize yield for these same four sites, using present and 2055 weather. The 2055 weather appears to reduce the probability of high maize yields at the Mozambique, Tanzania, and Zambia sites. Maize yields at the DRC site are predicted to be badly affected by the 2055 weather regime at the lower end of the yield spectrum, although the probabilities of obtaining yield above about 1.7 t /ha (conversion: 1 metric ton (t) = 1 Mg) are almost the same as at present. Conversely, the lower yield probabilities are strongly conserved at the Zambia site, but higher yields become far less probable. Yields at the Mozambique site are uniformly low and almost always in the 1–2 t/ha range, although the probability of achieving 2 t/ha is lower in the 2055 scenario.

Fig. 4. Cumulative maize yield probabilities [conversion: 1 t (metric ton) = 1 Mg] for present and simulated 2055 climates in the four sample zones.

Resource management must take these differences into account. At the Mozambique site, a low but constant source of domestic food supply may free resources for other enterprises, whereas, for the other three sites, domestic and regional food stocks might have to be stored to cover shortfalls arising from maize crop failure.

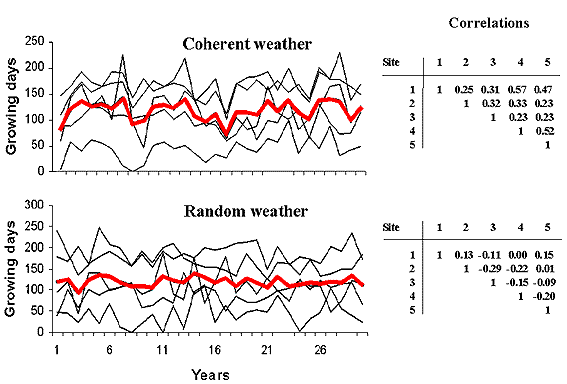
Weather coherence

Weather coherence, that is, the fact that weather conditions in a region or area are generally spatially correlated, might be expected to be of considerable importance. Fig. 5 (at left) shows an example, with the number of growing days (our proxy for pasture production) for five randomly selected sites in Zone 8 (one of the 51 weather zones located mostly in central Zimbabwe). The bottom graph shows the situation in which weather in Zone 8 is assumed to be independent, i.e., what occurs at any site in Zone 8 has no impact at all on the weather experienced at any other site. The heavy red line shows the mean number of growing days. The pattern of growing days by season appears to be random; the correlation matrix for the random weather also bears this out. The top graph shows the number of growing days for the same five sites in Zone 8, this time with coherent weather. To simulate coherent rainfall at each site, the same set of normal deviates was used each year to resample the baseline rainfall probits, as outlined previously. A stronger pattern in the number of growing days is seen. Year 17 provides a good illustration of a “poor” year when, for at least four of the five sites, the number of growing days is close to the lowest number experienced in the 29 replicates. The correlation matrix in Fig 5 (at right) indicates the “interdependence” of the weather experienced at these five sites.

Fig. 5. An example of the effect of weather coherence on five sites within a coherence zone. The zone average (red line) is much more stable in random climates. The correlation matrices show the degree of dependence in the coherent samples.

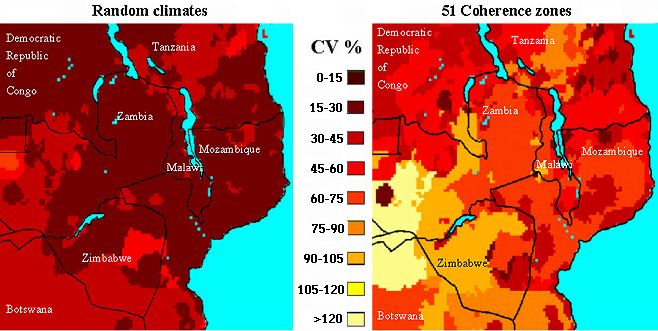
Figures 6 and 7 further illustrate the importance of coherence (and of being able to account for it). Fig. 6 shows the coefficients of variation in time (CVs) of the average rainfall per zone during the maize-growing season, using random and coherent present-day weather over the 51 zones for the study window. (The higher the CV, the lighter the map shade.) For these maps, the average was calculated across the sample points in each zone and the standard error of the time series was computed for each zone. For the area to the south of Lake Kariba, for example, the CV of rain increases from 22% to 107%, simply by imposing coherence on the zonal rainfall. The same effect appears in Fig. 7, which shows the CV of maize yield on soils of class 2 (moderately suitable for maize production). A general lightening of the map indicates substantial increases in the CV of simulated yield in response to imposing weather coherence within the 51 zones.

Fig. 6. The coefficient of variation of rainfall during the maize growing season, with random climates (left) and 51 coherence zones (right).

Fig. 7. The coefficient of variation of zonal maize yields on poor soils in random climates (left) and 51 coherence zones (right).

The implication is clear: in a region with a coherent weather system, if one site experiences bad conditions, then the chances are that other sites in the same region will also. Agricultural production will thus suffer both locally and regionally and, if coherence extends over a large area, continentally. In such cases, there may be profound implications for government policy (and marketing and transport) in attempting to ensure adequate food supply for many people over a potentially vast area.

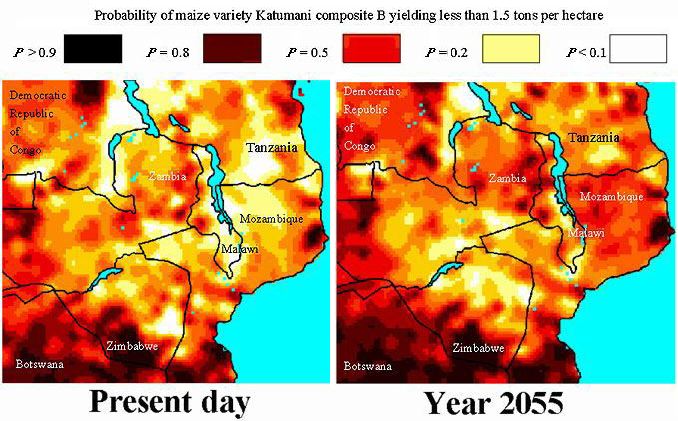
Maize and pasture performance

Figure 8 maps the overall simulated performance of maize as the probability of not achieving a yield of 1.5 t/ha using present and 2055-based weather (this figure was chosen arbitrarily, but is similar to current average maize yields on smallholder farms in the region). These values were calculated by computing the cumulative probabilities for the sample points in each zone. As an example, consider sample point number 104; located at 15.67 º S and 30.50 º E; it has the following Class 2 and 3 soil units:

Fig. 8. The probability that maize yields will fall below 1.5 t/ha (1t = 1 Mg) in (left) the present climate regime (left) and the simulated 2055 climate regime (right).

    Fh (humic Ferralsol): 10% area

    Fo (orthic Ferralsol): 20%

    Fx (xanthic Ferralsol): 10%

    Ge (eutric Gleysol): 20%

    Je (eutric Fluvisol): 10%

The rest of the pixel is taken up with a Class 1 soil. Five simulations were made using the characteristics of each soil unit. For display purposes, we assigned the eutric Gleysol and the eutric Fluvisol to Class 3, and the three Ferralsols to Class 2. Thus, for the map in Fig. 8, the simulated maize yields on the three Ferralsols were weighted by their relative occurrence to calculate the probabilities shown on the map.

Although an overall reduction in mean yields is apparent between the simulations carried out using the present-day and 2055 weather, in a few small zones, mean yields are actually simulated to increase between now and 2055. CERES-Maize accurately simulates the C₄ nature of the maize crop. Yields are predicted to increase in highland areas where the crop responds to rising temperatures. It should be borne in mind that these changes are also occurring along with a general increase in the standard deviation of maize yields, although these results are not shown here.

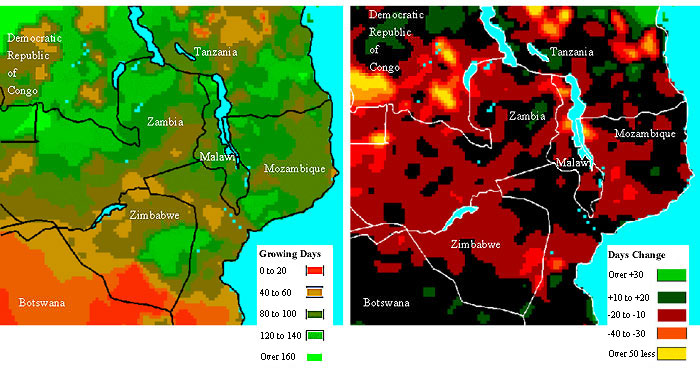
Figure 9 (at left) shows the average lower quartile of potential pasture-growing days in the 51 zones simulated using present and 2055-based weather. The actual number of growing season days is expected to fall below this in only one year out of four. As for the maize yields in Fig. 8, the change in this statistic (Fig. 9, at right) shows a general decline brought about by increased evaporation owing to increased temperatures being inadequately compensated by the small increase in monthly rainfall. In some areas, rainfall increases sufficiently to outweigh this effect.

Fig. 9. Lower quartile of the number of pasture-growing days: the average of present and 2055-based climate regimes (left), and the change from the present to 2055 (right).

The effects of global warming, in general, will lead to a reduction of maize yield and pasture, and to a greater risk. Small areas may actually benefit from the change, although they are not the same areas in each case. This may have serious implications for resource management, agricultural intensification, and population growth and movement.

Natural resource modeling is a highly scale-specific process; methods change with scale as wider spatial linkages are incorporated. We have demonstrated a method by which plot-level models can be run over large land areas and the results can be aggregated to provide information at the regional level. We have shown how the output from much lower resolution global models (in this case, a GCM) can be broken down using a higher resolution weather grid and an interpolation technique (for other methods, see Schulze 2000). The study has achieved an integration from process-level, plant-growth models to global climate models, the full gamut of the scaling problem.

Results of our study indicate that there may be substantial spatial shifts in maize cultivation in the region. Despite numerous uncertainties in the analysis, climate will clearly change by about 2055, with concomitant impacts on crop and livestock production. The highlands may become more suitable for maize (higher night temperatures and more rain, in places), whereas the marginal areas in the lowlands may become even more marginal and risky. Spatial shifts in maize production may arise as a result of climate change. These could be expected to have significant implications for regional maize-related agricultural research in the future and for the way in which technologies (such as different varieties, modified management practices, and improved water conservation practices) might be targeted. We will return to this issue.

Results of the study have also illustrated the importance of taking into account weather coherence in regional analyses. Using random weather patterns over a wide range of soil types can result in highly misleading simulations, because aggregation tends to lead to a general smoothing of the inherent weather variability in a region. This can markedly underestimate the variance of regional food supply and fodder availability.

Africa has been identified as the continent most vulnerable to the impacts of projected climate change on (among other things) agriculture and human health, largely because widespread poverty is expected to limit adaptation capabilities (IPCC 2001a). At the same time, human populations in Africa continue to grow, driving the intensification of agricultural production so that food production and income levels can be maintained (Staal et al. 2001). Agricultural systems in the region are thus highly dynamic, and climate change effects will surely contribute greatly to this dynamism in the coming decades.

We believe that methods such as the one we have outlined are potentially valuable in studying the impacts of climate change. At best, however, these are tentative first steps only. How can such tools and methods be converted into something much more comprehensive that can genuinely inform natural resource management issues at both community and policy levels? We will highlight three areas in which considerably more work is required.

First, the agricultural impacts of climate change have to be assessed at the level of the agricultural system. Smallholder mixed systems involving many different mixes of livestock and crops are very important in the region and in Africa in general. Interactions between crops and livestock are critical in maintaining soil fertility and providing dry-season feed for animals (Staal et al. 2001). In any meaningful assessment of possible system evolution in response to climate change, and to identify possible adaptation and mitigation strategies, clearly we need to be able to represent the major biological processes operating at the household level, as well as the objectives and attitudes of smallholders. There is a wide variety of crop and livestock models, but substantial work remains in combining these into robust systems models that can account for the major interactions between crops and livestock at the systems level (Thornton and Herrero 2001). In addition, although maize-based mixed systems are of particular importance to the rural poor in many areas of southern and eastern Africa, climate change impacts need to be studied in other systems such as mixed systems not based on maize, commercial crop–livestock systems, and pastoral systems. Further, climate change will induce changes in habitat suitability for important disease vectors such as mosquitoes, tsetse flies, and ticks (Hulme 1996). Studies are being undertaken on some of these (e.g., Rogers and Randolph 2000, McDermott et al. 2001). However, a great deal of work remains to be done before we have integrated models that can be used in concert with global circulation models (GCMs) to study the system impacts of climate change in a comprehensive fashion.

Second, a wide variety of different GCMs and GCM scenarios are available. There are inherent uncertainties in the outputs from all of these different models, arising from the way they have been constructed and parameterized. Even for the relatively simple analysis presented here, which involves only one crop and one variety, other GCMs and climate change scenarios could be used to assess the variation in GCM projections in terms of possible future maize and pasture production in the region. If this variation were to be relatively small, this would help to build confidence in the results of such scenario assessments. Convergence of results from widely differing impact assessment analyses would also assist greatly in clarifying and unifying the messages that could be distilled from them.

Third, we believe that a much better understanding is required of the information needs of decision makers with respect to natural resource management and the possible impacts of climate change. Policy decisions concerning natural resource management are taken at many levels, from the local community to national government. Information needs will thus vary widely, in terms of format, content, timing, and delivery mechanism, and probably in ways that are as yet imperfectly understood. An improved understanding of community and governmental decision-making processes could ultimately bring about much better matching of the demand for information of particular types with information supply from assessments of climate change impact. This applies to setting priorities for helping national agricultural research and extensions systems to make resource allocation decisions (e.g., is it worth investing in a breeding program for shorter duration bean varieties?). It applies equally to assisting in the identification of longer term adaptation options for rural communities that may be particularly vulnerable to climate change (e.g., are there other varieties and crops that can be grown to help diversify agricultural income, given likely changes in temperature regimes and rainfall patterns?).

The initial investigation reported here shows that plot-level process models could be integrated into large-scale, land use models that attempt to simulate agricultural production and use of resources at a landscape level. Evaluation of natural resource management options is a highly complex problem, and a great deal of work is still needed to produce systems models that are truly adequate for the task. Recent evidence shows clearly that the implications of climate change for rural poor people in Africa, in particular, may be enormous (IPCC 2001b). Despite their limitations, existing crop and livestock models, coupled with improved methods of downscaling GCM outputs, offer potentially fruitful pathways to the provision of climate change impact assessments that can help highly vulnerable rural poor people to adapt and cope.

Responses to this article are invited. If accepted for publication, your response will be hyperlinked to the article. To submit a comment, follow this link. To read comments already accepted, follow this link.

We thank two anonymous referees for very helpful comments on an earlier draft of this paper.

Batjes, N. H., editor. 1995. A homogenized soil data file for global environmental research: a subset of FAO, ISRIC, and NRCS profiles (Version 1.0). Working Paper 95/10, International Soil Reference and Information Centre (ISRIC), Wageningen, The Netherlands.

Batjes, N. H., and E. M. Bridges. 1994. Potential emissions of radiatively active trace gases from soil to atmosphere with special reference to methane: development of a global database (WISE). Journal of Geophysical Research 99(D8):16, 479-489.

Cullen, M. J. P. 1993. The unified forecast/climate model. The Meteorological Magazine 122:81-95.

Durand, W., and A. S. du Toit. 2000. Using crop growth models and GIS to address issues influencing sustainability in the short, medium and long term. Pages 101-105 in W. Durand and A. S. du Toit, editors. Proceedings of the Highveld Ecoregion Workshop on Methodology and Strategy Development Using Systems Analysis for Sustainability in the South African Highveld Ecoregion. ARC-Grain Crops Institute, Potchefstroom, South Africa.

Eastman, J. R. 1993. IDRISI Version 4.1 Technical Reference Manual. Clark University, Worcester, Massachusetts, USA.

FAO (Food and Agriculture Organization). 1974 . FAO-UNESCO soil map of the world 1:5 000 000. Volume 1, Legend. UNESCO, Paris, France, and FAO, Rome, Italy.

FAO (Food and Agriculture Organization). 1978. Report on the AgroEcological Zones project. Volume 1. Methodology and results for Africa. World Soil Resources Report 48. UNESCO, Paris, France, and FAO, Rome, Italy.

FAO (Food and Agriculture Organization). 1995. Digital soil map of the world and derived soil properties. Version 3.5. Land and Water Digital Media Series 1, FAO, Rome, Italy.

Hartkamp, A. D., K. de Beurs, A. Stein, and J. W. White. 1999. Interpolation techniques for climate variables. NRG-GIS Series 99-01. International Maize and Wheat Improvement Center (CIMMYT), Mexico City, Mexico.

Hassan, R. M., editor. 1998. Maize technology development and transfer. A GIS application for research planning in Kenya. CAB International, Wallingford, UK.

Hulme, M., editor. 1996. Climate change and southern Africa: An exploration of some potential impacts and implications in the SADC region. Report commissioned by WWF International and co-ordinated by the Climatic Research Unit, University of East Anglia, Norwich, UK.

IPCC (Intergovernmental Panel on Climate Change). 2001a. The regional impacts of climate change: an assessment of vulnerability. [Online] URL: http://www.ipcc.ch

IPCC (Intergovernmental Panel on Climate Change). 2001b. Climate change 2001: the scientific basis. Working Group 1 contribution to the IPCC Third Assessment Report. [Online] URL: http://www.ipcc.ch

Johns, T. C., R. E. Carnell, J. F. Crossley, J. M. Gregory, J. F. B. Mitchell, C. A. Senior, S. F. B. Tett, and R. A. Wood. 1997. The second Hadley Centre coupled ocean–atmosphere GCM: model description, spinup and validation. Climate Dynamics 13:103-134.

Jones, P. G., and P. K. Thornton. 1993. A rainfall generator for agricultural applications in the tropics. Agricultural and Forest Meteorology 63:1-19.

Jones, P. G., and P. K. Thornton. 1997. Spatial and temporal variability of rainfall related to a third-order Markov model. Agricultural and Forest Meteorology 86:127-138.

Jones, P. G., and P. K. Thornton. 1999. Fitting a third-order Markov rainfall model to interpolated climate surfaces. Agricultural and Forest Meteorology 97:213-231.

Jones, P. G., and P. K. Thornton. 2000. MarkSim: Software to generate daily weather data for Latin America and Africa. Agronomy Journal 92(3):445-453.

McDermott, J. J., P. M. Kristjanson, R. L. Kruska, R. S. Reid, T. P. Robinson, P. G. Coleman, P. G. Jones, and P. K. Thornton. 2001. Effects of climate, human population and socio-economic changes on tsetse-transmitted trypanosomosis to 2050. In S. J. Black and J. R. Seed, editors. World class parasites. Volume 1. The African Trypanosomes. Kluwer Academic Press, Dordrecht, The Netherlands. In press.

Mitchell, J. F. B., T. C. Johns, J. M. Gregory, and S. Tett. 1995. Climate response to increasing levels of greenhouse gases and sulphate aerosols. Nature 376:501-504.

Muchena, P., and A. Iglesias. 1995. Vulnerability of maize yields to climate change in different farming sectors in Zimbabwe. Pages 229-239 in C. Rosenzweig, L. H. Allen Jr., L. A. Harper, S. E. Hollinger, and J. W. Jones, editors. Climate change and agriculture: analysis of potential international impacts. American Society of Agronomy. Special Publication Number 59. Madison, Wisconsin, USA.

NOAA (National Oceanographic and Atmospheric Administration). 1984. TGP-OO6 D. Computer-compatible tape. NOAA, Boulder, Colorado, USA.

Richardson, C. W. 1985. Weather simulation for crop management models. Transactions of the American Society of Agricultural Engineers 28(5):1602-1606.

Ritchie, J. T., U. Singh, D. C. Godwin, and W. T. Bowen. 1998. Cereal growth, development and yield. Pages 79-98 in G. Y. Tsuji, G. Hoogenboom, and P. K. Thornton, editors. Understanding options for agricultural production. Kluwer Academic, Dordrecht, The Netherlands.

Rogers, D. J., and S. E. Randolph. 2000. The global spread of malaria in a future, warmer world. Science 289:1763-1766.

Schulze, R. 2000. Transcending scales of space and time in impact studies of climate and climate change on agrohydrological responses. Agriculture, Ecosystems and Environment 82:185-212.

Staal, S. J., S. Ehui, and J. C. Tanner. 2001. Livestock–environment interactions under intensifying production. Pages 345-364 in D. R. Lee and C. B. Barrett, editors. Tradeoffs or synergies? Agricultural intensification, economic development and the environment. CAB International, Wallingford, UK.

Thornton, P. K., and M. Herrero. 2001. Integrated crop-livestock simulation models for scenario analysis and impact assessment. Agricultural Systems 70(2-3):581-602.

Thornton, P. K., and P. W. Wilkens. 1998. Risk assessment and food security. Pages 329-346 in G. Y. Tsuji, G. Hoogenboom, and P. K. Thornton, editors. Understanding options for agricultural production. Kluwer Academic, Dordrecht, The Netherlands.

Thornton, P. K., A. R. Saka, U. Singh, J. D. T. Kumwenda, J. E. Brink, and J. B. Dent. 1995. Application of a maize crop simulation model in the central region of Malawi. Experimental Agriculture 31:213-226.

Tsuji, G. Y., G. Hoogenboom, and P. K. Thornton, editors. 1998. Understanding options for agricultural production. Kluwer Academic, Dordrecht, The Netherlands.

Walker, T. S., and J. G. Ryan. 1990. Village and household economics in India’s semi-arid tropics. Johns Hopkins University Press, Baltimore, Maryland, USA.