|
|
|
Copyright © 2001 by The Resilience Alliance
The following is the established format for referencing this article:
Packer, L. and R. Owen. 2001. Population genetic aspects of pollinator decline. Conservation Ecology 5(1): 4. [online] URL: http://www.consecol.org/vol5/iss1/art4/
A version of this article in which text, figures, tables, and appendices are separate files may be found by following this link.
Synthesis, part of Special Feature on Pollinator Decline Population Genetic Aspects of Pollinator Decline Laurence Packer1 and Robin Owen2
1York University; 2Mount Royal College and University of Calgary
- Abstract
- Introduction
- Methods
- Results
- Discussion
- Recommendations
- Responses to this Article
- Literature Cited
We reviewed the theory of conservation genetics, with special emphasis on the influence of haplodiploidy and other aspects of bee biology upon conservation genetic parameters. We then investigated the possibility that pollinator decline can be addressed in this way, using two meta-analytical approaches on genetic data from the Hymenoptera and the Lepidoptera. First, we compared levels of heterozygosity between the orders. As has been found previously, the haplodiploid Hymenoptera had markedly lower levels of genetic variation than the Lepidoptera. Bees had even lower levels, and bumble bees, in particular, often seemed almost monomorphic genetically. However, the statistically confounding effects of phylogeny render detailed interpretation of such data difficult. Second, we investigated patterns of gene flow among populations of these insects. Hymenoptera were far more likely to show genetic effects of population fragmentation than are Lepidoptera, even at similar geographic distances between populations. The reduced effective population sizes resulting from haplodiploidy probably contributed to this result. The proportion of species with low levels of gene flow did not vary among the different taxonomic groups within the Hymenoptera.
KEY WORDS: bumble bees, effective population size, gene flow, haplodiploidy, heterozygosity, Hymenoptera, Lepidoptera, meta-analysis, pollinator decline, population fragmentation, population genetics.
Published: April 5, 2001
Many environmental variables influence the long- and short-term survival of pollinator populations (Cane 2001, Marlin and LaBerge 2001, Roubik 2001), and thereby also the plants that they pollinate (e.g., Neff and Simpson 1993, Kevan and Phillips 2001), although this is not necessarily always the case (Thomson 2001). However, even if ecological factors are conducive to the long-term stability of a moderate-sized or small population, intrinsic genetic processes may lead to its eventual demise (Lande 1999). Despite the fact that the study of conservation genetics has been around for over 20 years (Frankel and Soulé 1980, Soulé 1980), very little attention has been given to potential genetic influences in pollinator decline. For example, the index of a recent book on butterfly conservation (Pullin 1995) refers to genetics only once, and a book entitled The conservation of bees (Matheson et al. 1996) does not refer to it at all. In this paper, we explore the possibility of genetic causes for pollinator decline.
Although evidence for the role of genetic factors in extinction is denied, or at least underplayed, by some (Caro and Laurenson 1994, Caughley 1994), there are authors at the other extreme who believe that many extinction events ascribed to demographic or stochastic causes actually have a largely genetic basis (Frankham 1995a), or that genetic effects may be more important than demographic ones even at reasonable population sizes (Lande 1994). Genetic causes of population decline come from a variety of influences, including the accumulation and expression of deleterious or lethal alleles or loss of fitness through lack of heterozygosity (Allendorf and Leary 1986, Mitton 1993). Such influences may arise quickly, as in the case of inbreeding depression, or they may have longer term effects, such as impeding adaptation to environmental change (Fisher 1930, Lande and Shannon 1996). Although much of the evidence for the most extreme example of genetic imperilment, the cheetah (O'Brien et al. 1983), has been cast into doubt (Caro and Laurenson 1994, Caughley 1994, Merola 1994), there remain many good examples that inbreeding depression has played a role in the demise of some populations (reviewed by Ralls and Balou 1986, Quattro and Vrijenhoek 1989, Frankham 1995a, Landweber and Dobson 1999), including those of potential pollinators (Saccheri et al. 1998). Of particular concern in a rapidly changing environment is the reduced potential for evolutionary response as a result of diminished genetic variation in fragmented populations (Fisher 1930, Frankel and Soulé 1981, McCauley 1993).
In this paper, we first outline the principles of conservation genetics as they relate to levels of genetic variation and gene flow. We do this in some detail for two reasons. First, treatments of pollinator conservation have generally ignored genetic aspects. Second, we hope that by outlining the principles of conservation genetics, this approach to pollinator biology will begin to receive the attention it deserves. In the second section, we discuss the particular biological attributes of the major group of pollinators, the bees, that might influence conservation genetic parameters. Bee biology differs from that of most other pollinators in several ways that are likely to be important for conservation genetics. The most important of these are (1) haplodiploidy, (2) nest construction combined with central place foraging, and (3) social evolution. Third, we summarize findings of preliminary analyses of surveys of genetic variation and gene flow in Lepidoptera and Hymenoptera, the details of which will be presented elsewhere. We do not restrict our analysis of the Hymenoptera data from just bees for several reasons. First, for many variables of interest, there are few data for this group. Second, we wanted to investigate whether the patterns in important conservation-genetic parameters in bees are a result of features specific to them, or whether they are shared by other subgroups of Hymenoptera or the order as a whole. Finally, we make some recommendations regarding pollinator conservation genetics and we note future research needs.
Population Genetics Principles1. Heterozygosity and effective population size
Reduced levels of genetic variation can result in inbreeding depression, lead to extinction through the extinction vortex (Gilpin and Soulé 1986, Lacy 1993), reduce a population's ability to withstand short-term environmental perturbation (Allendorf and Leary 1986), and make it more difficult for adaption to long-term environmental change (Fisher 1930, Soulé 1980). That levels of genetic variation are correlated with population size was first clearly demonstrated by Soulé (1976), and this conclusion has been more recently verified by Frankham (1996). Thus, populations of small size, presumably already facing demographic and other difficulties, are also at risk of extirpation for genetic reasons.
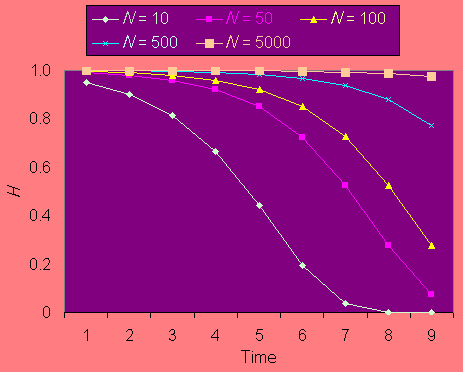
Heterozygosity is expected to decline over time in small populations according to the equation Ht = (1 - 1/2Ne)tH0, where Ht is heterozygosity in generation t, H0 is initial heterozygosity, and Ne is the effective population size. Fig. 1 shows the predicted decline of heterozygosity in populations of different sizes for up to 256 generations. For most pollinators with one generation per year, anthropogenically determined habitat loss and fragmentation in North America may be expected to have lasted between 30 and 150 years. Thus, populations of 100 and below will have suffered substantial loss of genetic variation since agricultural settlement.
|
Fig. 1. Reduction in heterozygosity Hexp over time for different mean population sizes.
|
The population size we need to consider in assessing heterozygosity loss is not the actual number of adults, but rather the harmonic mean of the effective population size over many generations. At any one point in time, the effective population size is expected to be substantially less than the actual number of individuals as a result of sterility, reduced fecundity, variance in fecundity, and sex-ratio effects, among other variables. In populations of animals in general, it is thought that Ne varies between one-half and one-tenth of the actual number of adults censused (Frankham 1995a, b). The harmonic mean of the effective population size over time is the important variable for determining expected levels of genetic variation. Thus, occasional decreases to small population size, such as population bottlenecks, will have a disproportionately large negative effect on Ne and any variance in population size over time will diminish long-term average Ne and consequently Hexp (Barrett and Charlesworth 1991, Leberg 1992, Hartl and Pucek 1994).
Fig. 2 demonstrates the effect of considering the harmonic, rather than the arithmetic, mean upon the effective population size for bottlenecks of 50% and 90% of the "stable" population size and occurring with different frequency. If population reductions occur half of the time, the effective population size, as measured using the harmonic mean, is considerably reduced in comparison to its arithmetic mean. There are well-known examples of precisely such intergenerational fluctuations in numbers. For example, the Karner blue butterfly Lycaeides melissa samuelis has two generations per year, with the spring generation approximately one-third as large as the summer one (Packer et al. 1998). The harmonic mean size of a population that alternates between 250 and 750 individuals (these numbers were estimated for some years for the Ontario population of this species; Packer 1994) is 375 in comparison to an arithmetic mean of 500. It should be noted that these numbers are total population sizes, and that effective population sizes would, in all cases, be substantially less than those quoted here. Other organisms that have biennial population fluctuations include those influenced by ENSO events (Roubik 2001) and some social wasps (Archer 1985). Other participants in this volume have ably documented considerable annual fluctuations in population size of various groups of pollinators, and have shown their populations to be highly unstable (Gilbert and Owen 1990, Cane 2001). We must realize that the actual population size to consider in assessing reduction in heterozygosity over time (as in Fig. 1), will always be less than we might expect based on the observed numbers of individuals in the field. Often it will be considerably less.
|
Fig. 2. Reduction in Ne resulting from population bottlenecks.

|
Lynch et al. (1995) have demonstrated that mutation accumulation in populations with effective sizes of 100 renders them highly vulnerable to extinction within 100 generations as a result of mutational meltdown. This result was obtained using explicit population genetic modeling and computer simulation with realistic estimates of the mutation rate. They note that increases in the mutation rate (which may occur, for example, with increased UV exposure or release of mutagenic pollutants) can greatly accelerate this process. Given that N e is often an order of magnitude less than the number of individuals censused, the results of Lynch et al. (1995) suggest that organisms with populations below 1000 may not be able to persist in the long term. Further reduction in effective population size is expected with metapopulation structure (Maruyama and Kimura 1980, Frankel and Soulé 1981, Gilpin 1991, McCauley 1991). This is because extinction and recolonization events will result in severe population bottlenecks. Especially in situations in which the number of founders per population is small, the effective population size of a metapopulation may be extremely small indeed. This effect is magnified by variance in the number of colonists because it is the harmonic mean of the number of colonists that influences their effective number (Whitlock and McCauley 1990). Thus, occasional colonization by small numbers of migrants when larger numbers are more commonly found will have a disproportionate and negative effect upon the effective population size of a metapopulation.
Frequent local extinction and recolonization can reduce the effective population size by several orders of magnitude (Wright 1931, Maruyama and Kimura 1980, McCauley 1993, Hedrick 1996). Gilpin (1991) has modeled the effects of metapopulation structure on heterozygosity, and has shown that all variation may be lost comparatively quickly. Similarly, the probability of two alleles being identical by descent in a population generally increases as the number of subpopulations increases (for a constant total population size), as the extinction and recolonization rates increase, and under propagule-pool recolonization rather than migrant-pool recolonization (McCauley 1991). These two recolonization schemes differ in that with the latter, all populations contribute migrants, whereas in the former, only one population produces the colonizers for any one recolonization event.
Empirical investigations of pollinator metapopulations have rarely been able to address the precise nature of metapopulation structure using direct methods. Seufert and Grosser (1996) found that migrants were more likely, per capita, to come from smaller subpopulations in the butterfly Chazara briseis. Hill et al. (1996) found the same pattern for a metapopulation of silver-spotted skipper butterflies, Hesperia comma, but they concluded that the population structure of H. comma, and probably that of most other organisms, is unlikely to provide a close fit to any of the theoretical metapopulation types.
Based upon these considerations, one can predict that organisms particularly prone to extinction for genetic reasons would have a metapopulation structure of one stronghold that serves as a source for the remaining populations, which have a high extinction rate. It is probable that many organisms living in early successional environments often exhibit a population structure similar to this. Harrison et al. (1988) have suggested that butterflies commonly persist in just this kind of metapopulation.
2. Gene flow among populations
Gene flow among populations can be estimated using direct or indirect methods. Direct methods require detailed fieldwork because movements of individuals between populations must be observed. Indirect methods use allele frequencies for polymorphic genetic loci to estimate the amount of interpopulation migration required to generate the observed genetic data. The number of migrants per generation among populations can be estimated from F statistics according to the equation Nm = (1 - FST)/4FST (Wright 1951), where Nm is the product of population size and the proportion of migrants per generation (i.e., the mean number of individuals exchanged between populations per generation); and FST is the fixation index (Wright 1951). This method has been shown to be superior to those based on rare or private alleles (Slatkin and Barton 1989). However, it assumes that the loci are selectively neutral (or at least are not under strong selection), and more importantly, that the populations have been stable long enough to have achieved equilibrium for migration rates (Slatkin 1994, Hutchison and Templeton 1999). For a good recent summary of these methods and others with special reference to tree populations, see Sork et al. (1998).
Comparisons of direct and indirect methods have rarely been made (for a discussion of the relative merits of direct and indirect estimates see Peterson and Denno 1998b). However, there is one excellent study in which both variables were estimated with considerable rigor. Brookes et al. (1997) compared allozyme-based estimates of Nm with those obtained from an extensive mark-release-recapture program for the sedentary lycaenid butterfly Plebejus argus. The Nm values obtained were reasonably similar: 6.2 for allozymes and 10.2 by mark-release-recapture. That the indirect estimate is lower than the direct one may be expected because migrants may well not have been demographically equivalent to residents. Thus, the migrating individuals may have lower harmonic mean fecundities in their new location than the residents, as would certainly be the case if, for example, some of the migrant females had oviposited prior to dispersing. However, it should be noted that at least two other studies of insect dispersal have found indirect methods to underestimate observed dispersal (Coyne et al. 1982, Slatkin 1985).
A wide variety of molecular markers can be used to assess gene flow (for a review of the molecular and population genetic methods, see Roderick 1996). Ross et al. (1999) have shown for fire ants, Solenopsis invicta, that different types of neutral molecular marker provide reasonably similar estimates of gene flow, although values from different microsatellite loci are more consistent than those obtained with other types of markers (codominant and dominant RAPDs, neutral allozymes, and mt DNA). Conversely, loci known to be under strong selection give widely divergent estimates of migration rate. However, good agreement among different types of genetic markers is far from routine (e.g., see Haag et al. 1993). It must be acknowledged that the kind of detailed analysis of the biasing role of selection on measured gene flow estimates, as considered by Ross et al. (1999), is very rarely undertaken, Most of the estimates that we have found did not investigate whether selection was acting upon any of the loci.
Indirect methods of estimating Nm assume that the metapopulation has achieved equilibrium for migration rates among subpopulations. Thus, organisms that had extensive ranges in pre-agricultural times (with minor interruptions, at most), but that are now scarce and in fragmented remnant populations among which gene flow is impossible, will often give high estimates of Nm, even though they may currently be exchanging no migrants at all. It is probable that marked changes in distribution and continuity among populations have affected most organisms in North America in this way. When assessing estimates of Nm, one must remember that these values estimated using indirect methods are probably much higher than the actual number of migrants exchanged, as a result of such historical effects.
By plotting the pairwise estimates of Nm against interpopulation geographic distance, it is possible to investigate whether there is isolation by distance (IBD) among the populations (Slatkin 1993, Peterson and Denno 1998a). Although statistical testing of this relationship is complicated by the non-independence of data points, there should be a clear negative relationship in the data at equilibrium. Careful inspection of the resulting scatterplot can reveal different patterns among subsets of data (Slatkin 1993).
Porter and Geiger (1995) have commented that indirect estimates may not be useful at large interpopulation distances because equilibrium over large scales will only be reached very slowly. Given the climatic variation that has occurred throughout the Quarternary period, few temperate taxa will have reached equilibrium. This, however, is a testable hypothesis. If plots of gene flow estimates against distance become more noisy at large distances, this would support Porter and Geiger's argument. Conversely, if a negative trend of log(Nm) vs. log(distance) continues at larger distances, this would be evidence that equilibrium has been reached even over great distances.
Peterson and Denno (1998a) have shown that it is more important to include a large number of populations in an analysis than it is to use multiple variable loci to estimate Nm. They found no significant effect of the number of loci on the probability of detecting IBD, and concluded that even single-locus estimates are useful. In contrast, even though they limited their survey to studies incorporating data from at least seven populations, they found that the use of fewer than 15 populations appeared to influence the detection of IBD. Another useful result from IBD analysis is that one can estimate neighborhood population size from the point where the regression line crosses the y-axis, i.e., at a distance between populations of zero (Slatkin 1993). This is the mean effective population size of the populations.
Application of population-genetic principles to conservation practice has led to the development of the one-migrant-per-generation "rule" (Frankel and Soulé 1981, Mills and Allendorf 1996). This states that one immigrant per population per generation is sufficient to prevent the disruptive effects of genetic drift upon populations, while permitting sufficient local adaptation. Although population genetic theory states that drift will exceed the effects of gene flow only for Nm < 0.25, the higher figure has been considered necessary simply because fractions of individuals cannot be transported among sites. Much higher levels of gene flow are considered disadvantageous because they lead to resident populations becoming swamped by genes from elsewhere that are often adapted to different conditions. One migrant between populations per generation has been thought sufficient, irrespective of the population sizes, even though the immigration of one individual to a large population would seem to have less effect than its immigration into a small one. This apparent paradox is readily solved: drift is slower in larger populations; therefore, fewer immigrants per resident are required to counterbalance its effects.
The one-migrant-per-generation model (reviewed by Mills and Allendorf 1996) has many assumptions: (1) there is no geographic pattern to gene flow (an island model of migration); (2) there is selective neutrality and no mutation; (3) the census population size is the same as the effective population size; (4) immigrants are demographically equivalent to residents; and (5) subpopulations persist long enough to attain equilibrium. Of these, perhaps (3) through (5) are the most serious. The effective population size is commonly thought to approximate one order of magnitude less than the number of individuals observed; hence, more migrants per generation than may be expected based on census population sizes are required to reduce the effects of drift. Lack of demographic equivalence of migrants to residents can dilute the effect of the actual migrant numbers detected by direct methods. Thus, it is not surprising that, in the most detailed analysis of this for any potential pollinator, Brookes et al. (1997) found that the effective number of individuals of the silver studded blue butterfly, Plebejus argus, introduced to two localities (estimated by indirect genetic methods) was approximately half the number actually released. Lack of equilibrium in a metapopulation may increase or decrease the number of migrants required to prevent divergence (McCauley 1993). Divergence will be less likely if emigrants colonize a previously unoccupied site. Conversely, an increased number of migrants is required to prevent divergence if emigrants tend to settle in already occupied patches. This will happen if signals from conspecifics are received by dispersing individuals and attract them to occupied patches. Little is known of this in pollinators. Although attraction to occupied sites has been reported for the solitary mining bee Andrena flavipes (Butler 1965), similar studies of other taxa would be worth pursuing.
Based on these considerations, but recognizing the problems inherent in "cookbook prescriptions," Mills and Allendorf (1996) suggested that one is the absolute minimum number of migrants per generation required to prevent populations from drifting apart genetically, and that higher migration rates will often be required in practice (as was apparently evident to Wright [1931]). However, these authors considered that an Nm >10 would prevent local adaptation; they indicated that an Nm for managed populations of endangered species should generally be between 1 and 10.
Gene flow estimates, per se, do not allow us to conclude that any one species or group of species is endangered. This is because different population processes associated with endangerment may lead to both high and low estimated levels of Nm. Low levels of Nm may indicate insufficient cohesion among sampled populations to prevent genetic drift from leading to speciation, or even the likelihood that speciation has already occurred. Low estimates of gene flow may also indicate dangerous levels of population isolation such that extirpation of any of them is likely to be permanent, i.e., local extinction is unlikely to be followed by natural recolonization (although it is likely that simple field observation would be sufficient to conclude this without genetic analysis).
Conversely, high levels of Nm may result from factors other than high contemporary rates of gene flow. For example, they may be the result of historically high levels of gene flow that are no longer in operation. Alternatively, they may indicate ephemeral metapopulation structure with high extinction rates in which all but one, or a few, subpopulations have recently been extirpated, with subsequent recolonization from one, or a few, subpopulations. Especially when combined with low heterozygosity values, high estimates of Nm may indicate frequent local extinction and recolonization (Waller et al. 1987). This kind of metapopulation structure is unlikely to give a high probability of survival for the species as a whole unless the source population(s) is extremely large or the number of subpopulations is very high. Consequently, Nm values alone do not necessarily tell us much about the potential genetic problems that species may be experiencing. Interpretation of such data has should account for the particular details of the organism's ecology and, if possible, its history.
Attributes of bee biology relevant to conservation genetics1. The influence of haplodiploidy
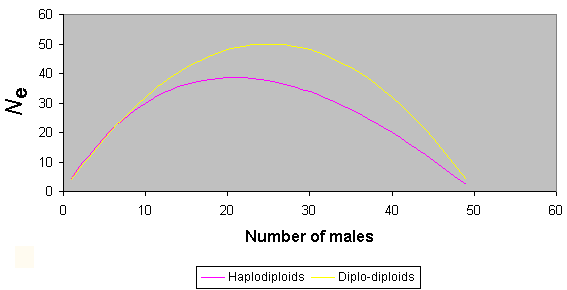
Because in any one generation (assuming an even sex ratio) there are only ¾ as many gene copies in haplodiploid organisms as in diplo-diploids ones, haplodiploids, such as bees, will generally have lower effective population sizes and, consequently, reduced heterozygosity. However, calculation of the effective population size is more complex in haplodiploids as a result of unusual sex ratio effects. It has been shown that if the sex ratio is less than 1:7 (males to females), the effective population size can be larger in haplodiploids than in diplodiploids with the same number of individuals of each sex (Crozier 1976). Fig. 3 shows variation in effective population size as a result of sex ratio biases in haplodiploids in comparison to those obtained in diplo-diploid organisms. Sex ratios sufficiently extreme to provide an increase of Ne in haplodiploids over that in diplo-diploids are commonly found in gregarious parasitoids (King 1987) and in other situations where sib mating is likely, as in fig wasps (Herre 1985) and some solitary vespids (Chapman and Stewart 1996). However, in the bees, female-biased sex ratios among reproductive individuals (i.e., omitting sterile workers from sex ratio calculations in social species) generally do not reach such extreme values. Thus, it is safe to assume that effective population sizes are smaller for bees and other haplodiploids than for diplo-diploid organisms with similar sex ratios and apparent population sizes, simply as a result of haplodiploidy.
|
Fig. 3. The influence of sex ratio upon effective population size for haplodiploids and diplo-diploids (for total population size of 50).
|
Two other biological attributes may interact with haplodiploidy to influence Ne: variance in family structure and inbreeding. Effective population size depends on the variance in progeny number per parent, which is assumed to follow a Poisson distribution (Hedrick and Parker 1997). Hedrick and Parker (1997) summarize recent arguments showing that variation in the number of female offspring per family will have a greater effect on Ne than variation in the number of male offspring. If the variance in offspring number is nil (i.e., all families have the same number of offspring), then Ne = 9N/4, where N is the number of parents. Now, if the number of females is constant across families but male production varies (according to a Poisson distribution), then Ne = 3N/2. Conversely, if male production is constant but the number of females varies, then Ne = 9N/10, which is considerably lower (Hedrick and Parker 1997). This latter production pattern may occur in some gregarious parasitoids in which a male is produced first, followed by one or more females before a second haploid egg is laid (King 1987). Haplodiploidy also influences the effect of inbreeding on the effective population size (Werren 1993). With highly female-biased sex ratios, inbreeding does not alter the effective population size of haplodiploids; with highly male-biased sex ratios, inbreeding reduces the effective population size by up to one-half with brother-sister mating. Highly male-biased numerical sex ratios are rare in Hymenoptera, but are known in honey bees (Page 1981) and bumble bees (Owen et al. 1980). However, multiple mating and other aspects of the mating system in Apis probably function as effective inbreeding avoidance mechanisms.
The question of whether haplodiploids have more, less, or the same amount of genetic load as do diplo-diploid organisms has been debated, and depends to a great extent on what assumptions are made. In simplest terms, genetic load arguments compare the mutation-selection balance equilibrium found at haplodiploid loci with that at diplo-diploid loci. It is a standard result that the equilibrium frequency of individuals with the lowest fitness is 25% less in haplodiploids (Hedrick and Parker 1997). However, Crozier (1985) pointed out that if genetic load is calculated in terms of loss of genetic material, then it is simply equal to the mutation rate and is the same for both haplodiploids and diplo-diploids. Werren (1993) relaxed some of the standard assumptions (such as allele frequencies being equal in both sexes, the deleterious allele being recessive, and selection being the same in both sexes), and showed that the genetic load in female haplodiploids is less, and in males is similar to that at autosomal loci in diplo-diploid organisms. He concluded that this will lead to reduced inbreeding depression resulting from genetic load in haplodiploids, and that inbreeding might arise more readily in organisms with this sex-determining mechanism, a point supported by Hamilton (1993). However, Werren's arguments did not include the influence of male diploidy. Further theoretical and empirical work clearly would be worthwhile in this area.
Levels of genetic variation are expected to be lower in haplodiploids than in diplo-diploids as a result of two factors in addition to reduced effective population size (Nagylaki 1981, Avery 1984, Owen 1993). (1) In each generation, deleterious alleles are directly exposed to selection in the haploid males, where there is no masking effect of dominance. Therefore, through purging selection, deleterious alleles will decrease in frequency more rapidly at haplodiploid loci than at comparable loci in diplo-diploids. Similarly, genes having a selective advantage will increase in frequency more quickly in haplodiploids than in diplodiploids. As a result, haplodiploids will show less transient genetic variation than diplo-diploids. (2) It is well known that conditions for a balanced polymorphism at a diallelic locus undergoing selection are more stringent for X-linked or haplodiploid loci than for auosomal or diplodiploid loci. In haplodiploids, heterozygous advantage is neither necessary nor sufficient to maintain a stable polymorphic equilibrium (Avery 1984). This is because five viabilities (three female and two male) must be balanced in haplodiploids, as opposed to three in diplo-diploids. The situation is more complicated for polymorphisms not maintained by heterozygous advantage because this requires differential selection between the sexes in diplo-diploids as well as in haplodiploids (Avery 1984, Owen 1985a). However, the probability of a polymorphism, and thus the resulting gene diversity, is still lower in haplodiploids than in diplodiploids (Pamilo and Crozier 1981). The three factors combined probably explain the observed lower levels of genetic variation in haplodiploid Hymenoptera and Thysanoptera (Crespi 1991) in comparison to other insects, although this interpretation is difficult to test statistically.
2. Diploid males
The haplodiploid sex-determining mechanism of the Hymenoptera provides an additional means whereby populations may decline as a result of genetic impoverishment. In these organisms (and presumably in other haplodiploids such as thrips, whitefly, certain beetles, etc.), sex is determined by genotypes at one or more hypervariable sex-determining loci (Whiting 1943, Crozier 1971, Camargo 1979). Heterozygotes are female and the hemizygous individuals (i.e., the haploids) are male. Diploid males arise with homozygosity at the sex-determining locus or loci. These males are often inviable (Petters and Mettus 1980) or highly infertile (Smith and Wallace 1971), or, if fertile, give rise to triploid female offspring (Smith and Wallace 1971, Garofalo and Kerr 1975). Hence, in all instances, they can be regarded as effectively sterile, and represent an inevitable genetic cost as a consequence of the system of sex determination. Although diploid males are expected in any finite population, clearly their numbers will increase if the effective population size is small or the inbreeding coefficient is high (Owen and Packer 1994). Thus, diploid males may be indicators of inbreeding and population fragmentation in Hymenoptera. Moreover, as already pointed out, diploid males are a drain on a population’s long-term chances of persistence because foraging effort aimed at female production yields a sterile male instead. Therefore, high levels of diploid male production will have an immediate negative effect upon the population.
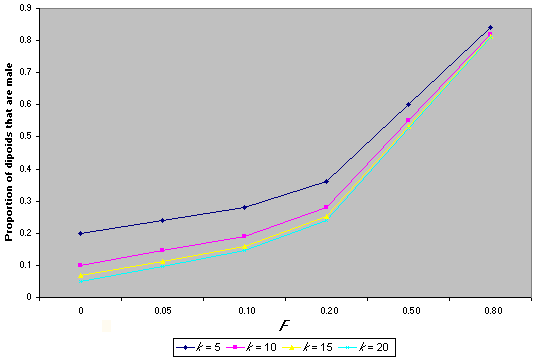
Diploid males have been detected in at least 33 species, and evidence suggests that single-locus sex determination is likely to prevail (Cook 1993). In this system, diploid males result from matings between a female and a male that have one sex-determining allele in common. These are called matched matings, and in a panmictic population at equilibrium (i.e., where all sex determining alleles are at equal frequency), they occur at a frequency phi = 2/k, where k is the number of sex-determining alleles (Adams et al. 1977). In natural populations, k is likely to range from 9 to19 (Adams et al. 1977). The proportion of diploid males in a population can be viewed in two ways, either as the proportion of diploids that are male, PHI, or as the proportion of males that are diploid, phi (Packer and Owen 1994). Operationally, the latter quantity is the most natural to estimate. However, it is the first quantity (PHI) that is directly related to the number of sex-determining alleles, k, whereas the proportion of males that are diploid, phi, also depends on the primary sex ratio (fertilized: unfertilized eggs). It is easy to show that, with inbreeding, PHI = (1/k) + FST (1- (1/k)). If the diploid: haploid ratio is 1:1, then phi = PHI/(1 + PHI). Fig. 4 shows how k and FST affect the proportion of diploid males in a hymenopteran population. Increase in the proportion of diploid males can occur if there is a reduction in k or an increase in FST, both of which could result from population fragmentation and isolation. These derivations are based on the assumption that diploid males are completely viable. If they have reduced viability, however, although they will still be produced as zygotes, the proportion in the adult population will decrease, leading to a change in the observed sex ratio (discussed in detail in Owen 1993).
|
Fig. 4. The effect of the number of sex determing alleles (k) and the inbreeding coefficient (F) on the proportion of diploids that are male in the Hymenoptera.
|
There are relatively few studies of diploid males in natural populations of hymenopteran pollinators (Packer and Owen 1990). Woyke (1976) studied brood mortality in honey bee hives in the Kangaroo Island bee sanctuary, South Australia, which has been in existence for more than a century. He estimated that only six sex-determining alleles were present in bees on the island, much less than the average of 18.9 in larger, non-isolated populations (Adams et al. 1977). Woyke (1976) attributed the low number of alleles to a combination of factors: the population was established from a small number of queens, so it is unlikely that all alleles would have been present in the founding population; commercial rearing practices may have led to some inbreeding; and in 1957 and earlier, intensive forest fires probably destroyed a high proportion of wild colonies.
Kukuk and May (1990) found diploid males in three out of four populations of the halictine bee Lasioglossum zephyrum. The frequency of diploid males was significantly greater (0.135) in one small, isolated population (Robinson) than in a large population (Salmon Creek A) where no diploid males were detected. The proportion of polymorphic loci was also lower in the Robinson population. Kukuk and May (1990) suggest that this implies that a bottleneck or small population size led to a reduction in the number of sex-determining alleles. When combined with the expectations of metapopulation structure in ground-nesting bees, diploid males may be a very sensitive measure of loss of genetic variation in bee populations.
Roubik et al. (1996) have found surprisingly high levels of diploid males in euglossine bees. Whether this is the result of chronically small effective populations of these bees (which certainly do not seem rare in comparison to other tropical bees) or indicates that they have evolved a mechanism preventing sterility in diploid males remains to be investigated.
3. Influence of nest, nest sites, and central-place foraging
Dense nest aggregations have been documented for many bee species. In some instances, these may persist for tens of years (as, for example, an aggregation of Lasioglossum malachurus on the Isle of Wight, which appears to have persisted at least since the 1920s; see also Knerer and Atwood [1967]). It is quite possible that nest aggregations start out from just one or a few mated females. Although this would be extremely difficult to observe, Michener (1966) noted that nests in a tiny, isolated aggregation of Lasioglossum versatum commonly exchanged nest mates, a situation that is unlikely in the absence of close genealogical relationship among individuals in different nests (Greenberg 1979). Strong philopatry has been observed in some bee species, and even in a situation in which females overwinter away from the nest site, they have been found to return and nest in very close proximity to their natal nest (Yanega 1990). Male behavior is relevant here in that even if females are strongly philopatric, more widely dispersing males may provide more extensive gene flow. There is almost no detailed information on this, although it is known for several aggregating species that males patrol territories of comparatively small area (Kukuk 1989). Whether this area includes their natal nest is not known. Long-duration philopatry and persistence of nest aggregations are likely to result in a metapopulation structure of the propagule-pool type, and thus may more likely to cause genetic impoverishment than if migration-pool population structure were in operation (McCauley 1993; see Introduction).
Some bee species have been recorded in dense aggregations in one year, but have been completely absent at the same location in the next year, although this kind of information is generally only anecdotal. Still other species exist in aggregations that build up over time and then crash (Knerer 1973). The causes of population decline are various, but have been attributed to three general classes. First, for ground-nesting bees, vegetation succession makes the nest site no longer suitable. This has been observed, e.g., in the aggregation of H. ligatus studied by Packer (1986), where the site became completely overgrown by legumes (L. Packer, unpublished observations). Second, succession may detrimentally affect some plant species that serve as pollen sources for particular bee species. This will result in extremely long-duration foraging trips and dramatically reduced productivity, even though the nest site may remain suitable. This has been observed in a Nova Scotian population of Lasioglossum comagenense that was extirpated after the bees could scarcely manage more than two pollen-foraging trips per day (L. Packer, unpublished observations). Third, populations may crash as a result of a build-up of natural enemies attracted to the large amounts of resources that build up in dense aggregations. These natural enemies may attack stored food supplies (cleptoparasites such as Sphecodes bees or mutillid wasps) or adult bees themselves, as do some robber flies (Asilidae; Knerer 1973). In no instance has the decline of an aggregation been ascribed to genetic causes. However, no studies have even attempted to assess this possibility.
Dispersal from temporarily suitable sites may lead to metapopulation structures more similar to the propagule-pool model, as large aggregations may build up over time and then crash, presumably with large number of adults emigrating. Analysis of genetic variation of Lasioglossum zephyrum along riverbanks in northern Pennsylvania and central New York revealed little differentiation among nest aggregations (Kukuk et al. 1987): 37 nest aggregations along nine creeks in three drainage areas were sampled, and data from eight polymorphic allozyme loci were collected. Using the method of Weir and Cockerham (1984) to determine the extent of macrogeographic subdivision of these populations, Kukuk et al. (1987) found that the coancestries (analogous to FST) were small, implying little differentiation among these nest aggregations. There was, however, a significant average inbreeding coefficient in these populations. Kukuk et al. (1987) inferred a dispersal pattern wherein some individuals migrate, but most mate and then remain in the area of their natal nest. Nonetheless, the precise metapopulation structure of any bee species remains to be investigated. For detailed examples of this kind of study in Lepidoptera, Brookes et al. (1997), Lewis et al. (1997), and Saccheri et al. (1998) provide excellent examples. Unfortunately, few bees are as easy to mark for fieldwork as are butterflies.
The central-place foraging of most bees also yields conservation-genetics consequences because all brood produced by a single female (or in a single nest for social species) arise in exactly the same location. This is likely to result in a more viscous population structure and, thereby, reduced gene flow. Few insect females deposit all of their eggs in one place, and most of them fly between oviposition events. The sibling larvae, which are variously mobile themselves, then develop sprinkled through the habitat and emerge as adults at various distances from one another. In contrast, the offspring of a female bee are usually produced within a single nest (for exceptions, see Packer 1993, Schmidt and Schmidt 1986). Emerging adults then arise from one precise location, and may or may not exhibit philopatry. When colony sizes are very large, as in honey bees, special mating behaviors seem to have evolved to prevent inbreeding (Seeley 1985). Even in primitively eusocial species with much smaller colony sizes, there is some evidence for inbreeding avoidance in that males habituate to familiar odors (Wcislo 1987).
4. The influence of sociality
The vast majority of bees are solitary (Michener 1974). Furthermore, eusocial species have to provision both worker and reproductive broods; with extremely few exceptions, this necessitates foraging at different times of the year. As a result, their likelihood of becoming oligolectic is reduced (for an exception, see Loken 1961). Thus, few oligolectic bees are eusocial.
Several complexities concerning effective population sizes result from eusociality. This type of social organization is common to many of the better known pollinators such as honey, stingless, and bumble bees, as well as many species of the less known sweat bees (Halictidae). As defined by Michener (1974), it involves a reproductive division of labour between queens and workers in which workers are the offspring of the queen (for a discussion of recent terminological controversies, see Wcislo [1997]). In eusocial societies, workers may produce a few haploid eggs; this worker production of males influences the effective population size and, consequently, the expected levels of heterozygosity. However, results are complex as the direction of the effect depends upon dominance relationships among the alleles and the selection regime (Owen 1985a). Unfortunately, there are very few data on the proportion of males that are produced by workers in social bees. For this, direct estimates using genetic markers are required, as estimates obtained from ovarian development indices appear to considerably overestimate worker male production (Packer and Owen 1994). Female production by mated workers is also known (Richards et al. 1995), but its effects on population genetic parameters remain uninvestigated.
Another aspect of sociality that will reduce the effective population size is the increased variance in family size to which it leads. Here, family size refers to the number of reproductive individuals only. Because colony reproductive productivity depends on both the number of workers produced by the foundress and the productivity and mortality rates of the workers, it may be expected that eusocial species will have a higher variance in family size than solitary insects. Some eusocial insects have varying proportions of semisocial colonies in spring (in semisocial colonies, nests are founded by more than one individual of the same generation, which then form a society with a reproductive division of labor among individuals of the same generation (Michener 1974). The number of workers produced by semisocial societies will tend to be higher than that produced by a solitary foundress, thereby further increasing variance in family size in the population as a whole (for productivity data for semisocial societies, see Packer [1993]). High variance in intercolony productivity is known for primitively eusocial bumble bees (Owen et al. 1980, Muller and Schmid-Hempel 1992) and halictines (Packer 1992). However, few comparable data are available for solitary species.
Whether social Hymenoptera actually do have lower levels of heterozygosity was the focus of some debate in the mid 1980s (Berkelhamer 1983, Graur 1985, Owen 1985b, Reeve et al. 1985). Although bumble bees and the more highly eusocial honey bees have unusually low levels of genetic variation, even for Hymenoptera, it is difficult to analyze these data statistically because of phylogenetic non-independence of the data points. What is needed is a set of comparisons for multiple independent origins of eusociality in the Hymenoptera, each paired with a solitary sister group. This remains to be done.
In this analysis, we restrict ourselves to studies using allozyme electrophoresis, simply because of the paucity of information using microsatellite or other more directly DNA-based methods. Additionally, it appears that microsatellite variation in Lepidopteran species is surprisingly low (e.g., Meglecz et al. 1998).
It is well known that Hymenoptera generally have lower levels of genetic variation than other insects (Metcalf et al. 1975, Pamilo et al. 1978, Lester and Selander 1979, Graur 1985, Crespi 1991, Owen 1993, Hedrick and Parker 1997). For haplodiploids, we have augmented the data presented by Crespi (1991) with more recent papers on this topic. For both orders under investigation, we obtained estimates of heterozygosity and gene flow from the literature by using recent reviews of the subject (Packer and Owen 1992, Packer et al. 1998, Peterson and Denno 1998b,) and additional literature searches using the key words genetic variation, heterozygosity, allozymes, electophoresis, gene flow, and population structure, associated with either of the taxon descriptors Lepidoptera or Hymenoptera.
Because estimates of Hexp may be influenced by the number of loci studied (Nei and Roychoudhury 1974, Singh and Rhomberg 1987; but see Shoemaker et al. 1993 and Packer et al. 1998), we followed Graur (1985) by including data only if they were based upon an unbiased sample of 15 or more loci. Papers in which data from variable loci only were reported, without reference to the number of invariant loci, were not included. Where heterozygosity estimates were presented for several different populations, we averaged the estimates. If the same species were investigated by more than one research group, we included each separate estimate because there are well-known "laboratory effects" on Hexp (Graur 1985; see also Kukuk and May 1985). We use heterozygosity rather than the number of alleles (a more sensitive measure of loss of genetic variation) because of the obvious problems associated with sample sizes, both for numbers of loci and numbers of individuals, with the latter. These problems may be overcome, but the analyses required to take such variation into consideration are beyond the scope of this paper (see Brookes et al. 1997).
Because our focus here is to see whether genetic data may be useful in assessing endangerment of pollinator species, we do not greatly concern ourselves with testing determinants of differences in levels of heterozygosity. Rather, we simply observe the patterns and see if low levels may be associated with endangerment.
Gene flow
Comparatively few estimates of Nm are available from the literature, especially for Hymenoptera. For this order, none of the data available come from endangered species or populations. We often calculated Nm from published tables of allele frequencies, using the program BIOSYS (Swofford and Selander 1989). Because gene flow levels are expected to decline with distance, comparisons of Nm estimates that do not take geographic distances between sample sites into consideration are not meaningful (Peterson and Denno 1998b). Mean distances among populations sampled were even less commonly provided in the literature. If maps with scales showing the sample locations were presented, we estimated the mean interlocality distance from them. Otherwise, we located the sample sites on maps as accurately as possible, estimated interlocality distances, and averaged them for each study. Following Peterson and Denno (1998b), for herbivorous species that exhibit host plant races or strains, we included only within-host plant gene flow estimates. Similarly, in the case of missing data for particular allozyme loci/population combinations, we removed loci or populations from the calculation in a manner that minimized data loss (Peterson and Denno 1998b).
We do not make any claims concerning the reality of taxonomies below the level of species, but simply follow the usage employed by the various authors. However, we would like to note that many apparently "good" species become two or more species when subjected to genetic analysis (Packer and Taylor 1997. Even in the absence of discrete genetic differentiation, it is clear that many populations deserve treatment as evolutionarily significant units (Moritz 1994, Legge et al. 1996, Packer et al. 1998).
We have presented our data graphically, plotting log(Nm) vs. log(average interlocality distance). This is equivalent to the approach taken to detect isolation by distance. However, we are using each study/species as an independent point and are using the resulting patterns as an exploratory tool only. This approach was taken by Veith et al. (1996) in their study of eight insect species of the semiarid porphyry landscapes of Germany. These authors obtained a clear negative relationship between the two variables.
We use data from allozyme, rather than microsatellite and other DNA-based, data simply because of the comparative paucity of data from the latter methods. It has been noted that the comparative rarity of highly variable microsatellite loci in Lepidoptera often renders this class of molecular markers less useful than allozymes for estimating gene flow (e.g., Meglecz et al. 1998).
Again, we are not overly concerned with explaining observed patterns in gene flow; rather, we wish to use this approach to decide whether it is possible to detect conservation genetic problems using this method.
Statistical AnalysisMany of the statistical analyses that one might wish to perform on data such as ours are rendered inappropriate because the data points are not phylogenetically independent (Ridley 1983). However, as previously noted, our focus is not explanatory. We wish to ask two related questions. First, do endangered species (or subspecies) have reduced levels of genetic variation in comparison to their non-endangered relatives? Second, do endangered species (or subspecies) have reduced levels of gene flow among populations in comparison to non-endangered related taxa? Consequently, we perform simple statistical analyses that do not correct for the confounding effects of phylogeny.
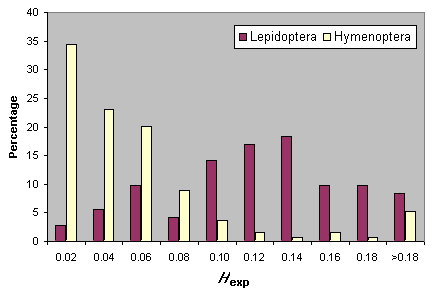
Heterozygosity estimates for Hymenoptera and Lepidoptera are summarized in Fig. 5. For neither taxon are there significant relationships between Hexp and either the number of loci sampled or the mean number of individuals surveyed. It is clear that Lepidoptera, as a group, have higher heterozygosity levels than the Hymenoptera (Fig. 5).
|
Fig. 5. Heterozygosity in Lepidoptera and Hymenoptera.
|
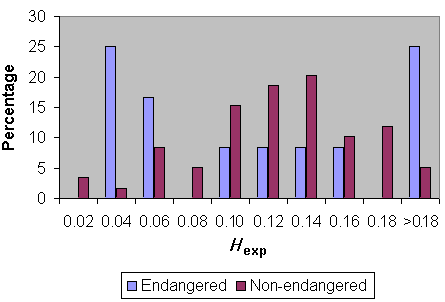
Fig. 6 compares heterozygosity for Lepidopteran species classified as not endangered vs. endangered (including those species having one or more subspecies classified as endangered or being classified as endangered for a large part of their total range). Clearly, there are more endangered species at the lower end of heterozygosity values. However, proper analysis of these data requires phylogenetic independent assessments.
|
Fig. 6. Heterozygosity in endangered and non-endangered Lepidoptera.
|
Fig. 7 shows the patterns of heterozygosity among the various subgroups of Hymenoptera. As can be seen, most of the high levels have been obtained from sawflies, and many of the low estimates come from bees. Nonetheless, comparatively high heterozygosity levels are not completely lacking for bees (Packer and Owen 1990).
|
Fig. 7. Heterozygosities for various groups of Hymenoptera.

|
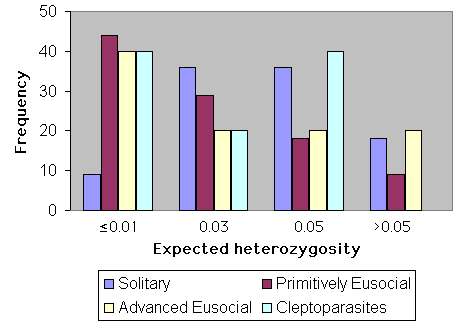
The influence of social behavior upon heterozygosity is shown graphically in Fig. 8. Sample sizes for cleptoparasites and highly eusocial species are too low for meaningful comparison. However, primitively eusocial species (n = 39) have significantly less genetic variation than do solitary ones (n = 11; Mann-Whitney U test, U = 191, t = 2.02, P < 0.05). In this analysis, behaviorally polymorphic species (sensu Packer 1998) were not included.
|
Fig. 8. Heterozygosity and social behavior in bees.
|
Gene Flow
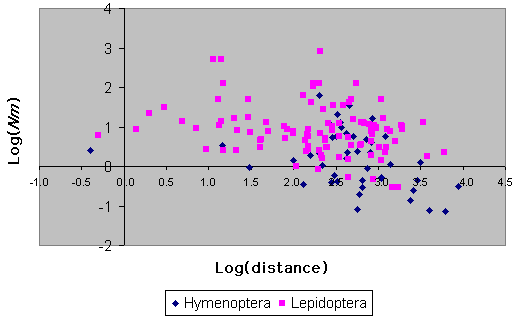
Estimates of gene flow among populations for both insect orders under consideration are plotted against mean interlocality distance in Fig. 9. There is no significant influence of the number of loci or the number of populations upon Nm for Hymenoptera (F = 0.0, P > 0.95, F = 0.03, P > 0.8 for the number of loci and populations, respectively). For Lepidoptera, there is no significant effect of the number of populations (F = 0.74, P > 0.39), but there is a significant negative relationship between Nm and the number of loci surveyed (F = 7.63, P = 0.007), although the amount of variation in Nm explained by the number of loci is very small (R2 = 0.5%). The slopes of log(Nm) against log(distance) are negative and significant for both orders, although the amount of variation in Nm that is explained by geographic distance is quite low (Lepidoptera, P = 0.007, R2 = 7.1%, n = 101; Hymenoptera, P = 0.009, R2 = 15.4%, n = 42).
|
Fig. 9. Log(Nm) vs. log(distance) for Hymenoptera and Lepidoptera.
|
It is clear from Fig. 9 that there are more low values for Hymenoptera than for Lepidoptera. For Nm values > 1, gene flow is sufficient to prevent the disruptive effects of drift (see Introduction). The proportion of Lepidoptera species with low Nm values is small: only 6/103 have values of around 1.0 or less. In contrast, the proportion of Hymenoptera with similarly low values is over one-third (18/44). This difference in frequency is statistically significant (R2 = 27.72, P << 0.001). This is not a result of the Hymenoptera data being based upon species with significantly longer distances between surveyed populations (for those taxa with low gene flow rates, comparing mean interlocality distance per species between Lepidoptera and Hymenoptera, Mann-Whitney U = 68, P > 0.1). Neither is the Hymenoptera result due to peculiarities of one particular subtaxon within this group, because all groups (Symphyta, Parasitica, Formicidae, Vespidae, and Apoidea) are represented in the low gene flow category in approximate proportion to their number in the data set as a whole (with Yates' correction, R2 = 7.5, P > 0.1). One reason for this difference between the orders is probably the lower effective population size conferred by haplodiplody, which leads to greater genetic drift even in populations with similar census population sizes.
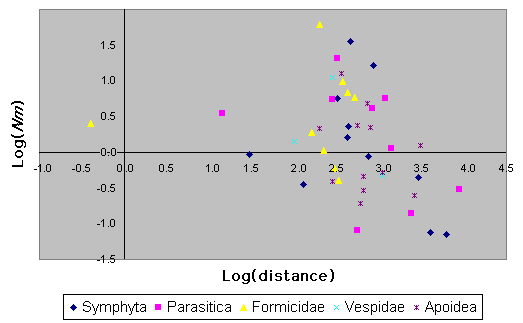
Variation in Nm vs. distance for various subtaxa of Hymenoptera is provided in Fig. 10. Phylogenetic non-independence of data and small sample sizes make this difficult to test statistically. Nonetheless, it appears from Fig. 10 that bees do not have markedly different patterns of isolation by distance than do the other taxa.
|
Fig. 10. Log(Nm) vs. log(distance) for various groups of Hymenoptera.
|
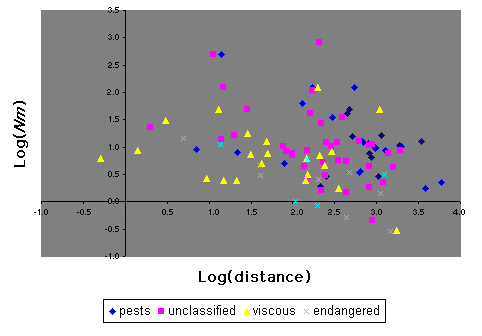
There is significant heterogeneity in the data for Lepidoptera when they are grouped into the four categories of (1) endangered, (2) viscous populations but not endangered, (3) pests, and (4) "other" (Fig. 11). A Kruskal-Wallis test of differences between median Nm values of these groups is significant (H = 10.0, P = 0.018). However, phylogenetic non-independence of the data renders this analysis suspect, as all but one endangered species is a butterfly and almost all pest species are moths. Of particular importance here is the comparison of Nm between endangered and non-endangered species. We performed this analysis with pests removed because they may be expected to have disproportionately large Nm values (inspection of Fig. 11 suggests that this is the case in at least some instances) and most are moths, whereas the endangered species are almost all butterflies. Endangered species of Lepidoptera have significantly lower Nm than non-endangered species (Mann-Whitney U = 2316, P = 0.003).
|
Fig. 11. Log(Nm) vs. log(distance) for various groups of Lepidoptera.
|
There is considerable variation in levels of heterozygosity among the two insect orders potentially of greatest importance as pollinators, with the Hymenoptera generally having lower levels. It is highly likely that reduced effective population size resulting from haplodiploidy is at least partly responsible for this. Among Lepidoptera, endangered species are more likely to have extremely low levels of heterozygosity than non-endangered species. Whether this is cause or effect remains to be demonstrated.
Is there evidence that low levels of heterozygosity decrease the chances of survival for a population of wild pollinators? For the Lepidoptera, there is one clear example in which the answer to this question is a definite yes. Saccheri et al. (1998) studied the genetics and demography of the Glanville fritillary, Melitaea cinxia, on the island of Aland in Finland. Between 1995 and 1996, seven out of 42 populations went extinct. Based upon detailed population monitoring and genetic analysis, these authors concluded that the probability of a population's extinction was affected not only by the demographic variables of its size, the trend in population size of neighboring populations, and the availability of adult nectaring sources, but also by levels of heterozygosity as estimated from one microsatellite and seven allozyme loci. Additional data provided information on life history parameters that were affected by heterozygosity. Thus, larval survival and mass at pupation were positively related and pupal duration and variance in egg hatch were negatively related to the proportion of heterozygous loci in the mother. Similarly, more heterozygous females had greater longevity.
No data on negative effects of reduced heterozygosity are available for any haplodiploid organism in the wild. Indeed, no data specifically address this situation, even under laboratory conditions, although Unruh and Messing (1993) suggest that failures of laboratory colonies of parasitoid biological control agents may commonly have occurred as a result of inbreeding depression.
Diploid male production clearly is of concern for populations of Hymenoptera with reduced levels of genetic variation and/or small effective population sizes, because with matched matings, their sterility leads to a considerable genetic mortality rate. It is interesting that, despite the potential problems associated with inbreeding and diploid male production, a number of Hymenoptera habitually have brother-sister mating. These include gregarious parasitoids (Hamilton 1993, Werren 1993) and some eumenine wasps (Cowan 1979). Chapman and Stewart (1996) estimated that brother-sister matings in the eumenine Ancistrocerus antilope were over 90%. Despite this, only 25% of the males that they collected were diploid. Whether additional diploid males suffered mortality after egg-laying but before censusing remains unknown. Diploid males in worker broods of eusocial species clearly reduce colony productivity (Plowright and Pallett 1979), although there are no field data on this.
Our plots of log(Nm) vs. log(distance) show a negative slope continuing up to the greatest distances found in our survey. This result, which holds for both orders, suggests that equilibrium may be reached even over enormous distances, contrary to the suggestions of Porter and Geiger (1995).
Endangered Lepidoptera species have significantly lower levels of interpopulation migration than do non-endangered species. There are no endangered species with high Nm values. This suggests that recent colonization of all populations from one source is not a metapopulation pattern common among endangered Lepidoptera. Rather, these data indicate that endangerment in butterflies seemingly occurs most often in populations that are already fragmented and somewhat genetically isolated.
Considerably more Hymenoptera than Lepidoptera have Nm values below the one-migrant-per-generation level. Among bees, two species have extremely low levels of interpopulation migration, as evinced by indirect methods: Halictus confusus and Lasioglossum boreale. This is interesting in light of the survey of population differentiation among Hymenoptera by Packer and Taylor (1997), who surveyed levels of genetic differentiation among populations of six taxonomically well-known bee species. Fixed genetic differences were found for five of the six species, suggesting that species-level divergence had already occurred. The sole exception was Halictus confusus. Our analysis based upon gene-flow estimates casts doubt on this conclusion. Thus, the only species surveyed by Packer and Taylor (1997) that definitely seemed to represent one genetic unit is either undergoing speciation or has already done so. Additional sampling is needed. For L. boreale, populations in the southern portion of its range exhibit fixed differences that may be indicative of species-level differentiation (Packer and Taylor 1997). However, even those that do not have fixed differences still have fairly high levels of genetic differentiation that indicate no, or very little, gene flow (J. Taylor and L. Packer, unpublished data). In the southern portion of its range, this species occurs only at high altitude on mountains at an elevation > 2900 m. Clearly, it is unreasonable to expect any gene flow between populations occurring in these moist, high-elevation sites through hundreds of kilometers of unsuitable desert habitat. It is probable that these populations have been isolated since the retreat of the glaciers beginning 16,000 years ago, giving plenty of time for divergence of these isolated and often small populations. Other low Nm values (< 1) for bees are for island populations of the bumble bee Bombus terrestris (Widmer et al. [1998]; this is not included in our survey as it is one of the few studies based upon microsatellites), populations of Halictus rubicundus from either side of the Rocky Mountains (Packer and Owen 1989), and populations of Lasioglossum marginatum obtained from Greece and France that may have been separated for a reasonable time if the French population spent the last glacial maximum in Spain isolated from more eastern populations (Blanchetot and Packer 1992). The only other bee species with low Nm is Lasioglossum villosulum (Packer et al. 1999), which was surveyed in two regions of France and for which no simple reason for low gene flow seems readily forthcoming. Additional sampling over a wider geographic range would be useful for all of these species.
There is a crucial need for initiating a conservation biology research program for haplodiploid organisms in general, and bees in particular, as these are the most important pollinators of all (Neff and Simpson 1993, Kevan and Phillips 2001). Our data suggest that bees and other haplodiploids have reduced heterozygosity and reduced levels of gene flow among populations in comparison to Lepidoptera, and, at least for heterozygosity, in comparison to diplo-diploid insects in general. There is some evidence that primitive eusociality further reduces values for these variables.
We do not have a good understanding of the empirical effect of haplodiploidy on conservation genetic parameters. Although this sex-determining mechanism probably confers a release from some deleterious effects of inbreeding (Werren 1993), it also leads to the production of sterile diploid males. The relative importance of these two factors remains to be investigated. Although experimental breeding and/or population cage work with readily maintained species such as alfalfa leafcutter bees would be particularly worthwhile, their long generation time means that results from such investigations will be a fairly long time in coming. Population cage experiments such as those done by Frankham and colleagues on Drosophila (e.g., Frankham and Loebel 1992, Frankham et al. 1993), but with hymenopterous parasites of Drosophila such as Asobara, might be informative. This would be a more rapid way to obtain results that might be of predictive value in the conservation genetics of bees.
One of the major findings of our literature review is that there has not been a single population genetic study of any oligolectic bee species, and almost no large-scale studies of any species, at least using allozymes. However, there are a few studies using microsatellites and other DNA-based methods. Widmer and Schmid-Hempel (1999) found no evidence for isolation by distance in a bumble bee, but its influence may have been masked by high genetic differentiation over small distances in samples obtained on either side of the alps. Estoup et al. (1996) and Widmer et al. (1998) found very low population differentiation among mainland populations of a different bumble bee species, but significant variation among islands and between island and mainland samples even over oceanic distances as small as 3 km.
Oligolectic bee species might be expected to be at the most risk of extinction from genetic or any other reasons, as they rely upon one, or a few closely related, species of plants as a food source. Of relevance here is the empirical finding of Peterson and Denno (1998a) that monophagous herbivorous insect species had much lower migration rates than polyphagous (but not oligophagous) species, at least up to geographic distances of 500 km. A comparative survey of levels of population differentiation among samples of oligolectic and polylectic bees, preferably collected at the same set of locations, would be of considerable interest and importance.
Most bees are central-place foragers; thus, they may be expected to have a more viscous population structure than most other insects. Cleptoparasites are an exception, in that they commonly fly from nest to nest, producing offspring over a comparatively wider area. It would be interesting to collect samples of host-specific cleptoparasitic bees and their hosts from a variety of locations to compare their levels of gene flow. Only one study of heterozygosity has compared data from cleptoparasitic bees and their hosts (Packer et al. 1995). Genetic diversity was very similar between the two pairs of species, but, given that the cleptoparasitic species were not host specific, the lack of reduced variation in the former may have been caused by larger local population sizes rather than by a less fragmented population structure.
We recommend the use of correlation plots of Nm against mean distance to assess the relative level of gene flow in a species of interest. However, results should be interpreted with caution because these indirect methods retain the influence of historic levels of gene flow that may no longer be operating. Furthermore, it is probable that, for the resulting Nm estimates to be reasonably accurate, larger than normal numbers of populations would have to be investigated. Peterson and Denno (1998b) recommend that at least 15 populations be surveyed.
As noted, Nm estimates alone cannot tell us much about the conservation genetics situation faced by a particular species. Because both high and low values may be indicative of impending extinction, other biological attributes must be taken into consideration. However, in our data set, there were no high values of Nm at short distances for any of the endangered Lepidoptera. In summary, the general interest provided by population genetic aspects of haplodiploidy, combined with the undoubted importance of bees as pollinators of crops and wild plants, suggests that bee conservation genetics deserve to be investigated seriously.
Responses to this article are invited. If accepted for publication, your response will be hyperlinked to the article. To submit a comment, follow this link. To read comments already accepted, follow this link.
Adams, J., E. D. Rothman, W. E. Kerr, and Z. L. Paulino. 1977. Estimation of the number of sex alleles and queen matings from diploid male frequencies in a population of Apis mellifera. Genetics 86:583-596.
Allendorf, F. W., and R. F. Leary. 1986. Heterozygosity and fitness in natural populations of animals. Pages 57-56 in M. E. Soulé, editor. Conservation biology: the science of scarcity and diversity. Sinauer, Sunderland, Massachusetts, USA.
Archer, M. E. 1985. Population dynamics of the social wasps Vespula vulgaris and Vespula germanica in England. Journal of Animal Ecology 54:473-485.
Avery, P. J.1984. The population genetics of haplo-diploid and X-linked genes. Genetic Research 44:321-341.
Barrett, S. C. H., and D. Charlesworth. 1991. Effect of a change in the level of inbreeding on the genetic load. Nature 352:522-524.
Berkelhamer, R. C. 1983. Intraspecific genetic variation and haplodiploidy, eusociality, and polygyny in the Hymenoptera. Evolution 37:540-545.
Blanchetot, A., and L. Packer. 1992. Genetic variability in the social bee Lasioglossum marginatum and a cryptic undescribed sibling species as detected by DNA fingerprinting and allozyme electrophoresis. Insect Molecular Biology 1:89-97.
Brookes, M. I., Y. A. Graneau, P. King, R. C. Owen, C. D. Thomas, and J. L. B. Mallet. 1997. Genetic analysis of founder bottlenecks in the rare British butterfly Plebejus argus. Conservation Biology 11:648-661.
Butler, C. G. 1965. Sex attraction in Andrena flavipes Panzer, with some observations on nest-site restriction. Proceedings of the Royal Entomological Society of London 40:77-80.
Camargo, C. A. 1979. Sex determination in bees. XI. Production of diploid males and sex determination in Melipona quadrifasciata. Journal of Apicultural Research 18:77-84.
Cane, J. H. 2001. Habitat fragmentation and native bees: a premature verdict. Conservation Ecology 5(1):3. [online] URL: http://www.consecol.org/vol5/iss1/art3
Caro, T. M., and M. K. Laurenson. 1994. Ecological and genetic factors in conservation: a cautionary tale. Science 263:485-486.
Caughley, G. 1994. Directions in conservation biology. Journal of Animal Ecology 63:215-244.
Chapman, T. W., and S. C. Stewart. 1996. Extremely high levels of inbreeding in a natural population of the free-living wasp Ancistrocerus antislope (Hymenoptera: Vespidea: Eumeninae). Heredity 76:65-69.
Cook, J. M. 1993. Sex determination in the Hymenoptera: a review of models and evidence. Heredity 71:421-435.
Cowan, D. P. 1979. Sibling matings in a hunting wasp: adaptive inbreeding? Science 205:1403-1405.
Coyne, J. A., I. A. Boussy, T. Prout, S. H. Bryant, J. S. Jones, and J. A. Moore. 1982. Long distance migration of Drosophila. American Naturalist 119:589-595.
Crespi, B. J. 1991. Heterozygosity in the haplodiploid Thysanoptera. Evolution 45:458-464.
Crozier, R. H. 1971. Heterozygosity and sex determination in haplo-diploidy. American Naturalist 105:399-412.
Crozier, R. H. 1976. Counter-intutive property of effective population size. Nature
Crozier, R. H. 1985. Adaptive consequences of male-haploidy. Pages 201-222 in W. Helle and M. W. Sabelis, editors. Spider mites: Their biology, natural enemies and control. Elsevier, Amsterdam, The Netherlands.
Estoup, A., M. Solignac, J.-M. Cornuet, J. Goudet, and A. Scholl. 1996. Genetic
differentiation of continental and island populations of Bombus terrestris (Hymenoptera: Apidae) in Europe. Molecular Ecology 5:19-31.
Fisher, R. A. 1930. The genetical theory of natural selection. Oxford University Press, Oxford, UK.
Frankel, O. H., and M. E. Soulé, 1981. Conservation and evolution. Cambridge University Press, Cambridge, UK.
Frankham, R. 1995a. Conservation genetics. Annual Review of Genetics 29:305-327.
Frankham, R. 1995b. Inbreeding and extinction: a threshold effect. Conservation
Biology 9:792-799.
Frankham, R. 1996. Effective population size/adult population size ratios in wildlife: a review. Genetical Research 66:95-107.
Frankham, R., and D. A. Loebel. 1992. Modeling problems in conservation genetics using captive Drosophila populations: rapid genetic adaptation to capivity. Zoo Biology 11:333 -342.
Frankham, R., G. J. Smith, and D. A. Briscoe. 1993. Effects on heterozygosity and reproductive fitness of inbreeding with and without selection on fitness in Drosophila melanogaster. Theoretical and Applied Genetics 86:1027-1037.
Garofalo, C. A., and W. E. Kerr. 1975. Sex determination in bees. I. Balance between femaleness and maleness genes in Bombus atratus Franklin (Hymenoptera: Apidae). Genetica 45:203-209.
Gilbert, F., and J. Owen. 1990. Size, shape, competition, and community structure in hoverflies (Diptera: Syrphidae). Journal of Animal Ecology 59:21-39.
Gilpin, M. 1991. The genetic effective size of a metapopulation. Biological Journal of the Linnean Society 42:165-175.
Gilpin, M. E., and M/ E. Soulé. 1986. Minimum viable populations: processes of species extinction. Pages 19-34 in M. E. Soulé, editor. Conservation biology: the science of scarcity and diversity. Sinauer, Sunderland, Massachusetts, USA.
Graur, D. 1985. Gene diversity in Hymenoptera. Evolution 39:190-199.
Greenberg, L. 1979. Genetic component of bee odor in kin recognition. Science 206:1095-1097.
Haag, K. L., A. M. Araújo, and A. Zaha. 1993. Genetic structure of natural
populations of Dryas iulia (Lepidoptera: Nymphalidae) revealed by enzyme polymorphism
and mitochondrial DNA (mtDNA) restriction fragment length polymorphism (RFLP).
Biochemical Genetics 31:449-460.
Hamilton, W. D. 1993. Inbreeding in Egypt and in this book: A childish perspective. Pages 429-450 in N. Wilmsen Thornhill, editor. The natural history of Inbreeding and outbreeding; theoretical and empirical perspectives. University of Chicago press, Chicago, Illinois, USA.
Harrison, S., D. D. Murphy, and P. R. Ehrlich. 1988. Distribution of the bay checkerspot butterfly, Euphydryas editha bayensis: Evidence for a metapopulation model. American Naturalist 132:360-382.
Hartl, G. B., and Z. Pucek. 1994. Genetic depletion in the European bison (Bison bonasus) and the significance of electrophoretic heterozygosity for conservation. Conservation Biology 8:167-174.
Hedrick, P. W. 1996. Bottleneck(s) or metapopulation in cheetahs. Conservation Biology 10:897-899.
Hedrick, P. W., and J. D. Parker. 1997. Evolutionary genetics and genetic variation of haplodiploids and x-linked genes. Annual Review of Ecology and Systematics 28:55-83.
Herre, E. A. 1985. Sex ratio adjustment in fig wasps. Science 22:896.
Hill, J. K., C. D. Thomas, and O. T. Lewis. 1996. Effects of habitat patch size and isolation on dispersal by Hesperia comma butterflies: implications for metapopulation structure. Journal of Animal Ecology 65:725-735.
Hutchison, W. D., and R. A. Templeton. 1999. Correlation of pairwise genetic and geographic distance measures: inferring the relative influences of gene flow and drift on the distribution of genetic variability. Evolution 53:1898-1914.
Kevan, P. G., and T. Phillips. 2001. The economics of pollinator declines: assessing the consequences. Conservation Ecology 5(1):8. [online] URL: http://www.consecol.org/vol5/iss1/art8
King, B. H. 1987. Offspring sex ratios in parasitoid wasps. Quarterly Review of Biology 6:367.
Knerer, G. 1973. Periodizitat und Strategie der Schmarotzer einer socialen Schmalbiene Evylaeus malachurus (K.). Zoologische Anzeiger 190:41-63.
Knerer, G., and C. E. Atwood. 1967. Parasitization of halictine bees in southern Ontario. Proceedings of the Entomological Society of Ontario 97:103-110.
Kukuk, P. 1989. Dispersal of males of the primitively eusocial sweat bee Dialictus zephyrum within a small nest aggregation. Sociobiology 15:1-7.
Kukuk, P. F., R. H. Crozier, D. R. R. Smith, G. C. Eickwort, and B. P. May. 1987. The population structure of a primitively eusocial sweat bee, Lasioglossum (Dialictus) zephrum. Page 384 in J. Eder and H. Bembold, editors. Chemistry and biology of social insects. Verlag J. Peperny, Munich, Germany.
Kukuk, P. F., and B. May. 1985. A re-examination of genetic variability in Dialictus zephyrus (Hymenoptera: Halictidae). Evolution 39:226-228.
Kukuk, P. F., and B. May. 1990. Diploid males in a primitively eusocial bee, Lasioglossum (Dialictus) zephyrum (Hymenoptera: Halictidae). Evolution 44:1522-1528.
Lacy, R. C. 1993. VORTEX: A computer simulation model for use in population viability analysis. Wildlife Research 20:45-65.
Lande, R. 1994. Risk of population extinction from new deleterious mutations. Evolution 48:1460-1469.
Lande, R. 1999. Extinction risks from anthropogenic, ecological, and genetic factors. Pages 1-22 in L. F. Landweber and A. P. Dobson, editors. Genetics and the extinction of species: DNA and the conservation of biodiversity. Princeton University Press, Princeton, New Jersey, USA.
Lande, R., and S. Shannon. 1996. The role of genetic variation in adaptation and population persistence in a changing environment. Evolution 50:434-437.
Landweber, L. F., and A. P. Dobson, editors. 1999. Genetics and the extinction of species: DNA and the conservation of biodiversity. Princeton University Press, Princeton, New Jersey, USA.
Leberg, P. L. 1992. Effects of population bottlenecks on genetic diversity as measured by allozyme electrophoresis. Evolution 46:477-494.
Legge, J. T., R. Roush, R. Desalle, A. P. Vogler, and B. May. 1996. Genetic criteria for establishing evolutionarily significant units in Cryan’s buckmoth. Conservation Biology 10:85-98.
Lester L. J., and R. K. Selander. 1979. Population genetics of haplodiploid insects. Genetics 92:1329-1343.
Lewis, O. T., C. D. Thomas, J. K. Hill, M. I. Brookes, T. P. R. Crane, Y. A. Graneau, J. L. B. Mallet, and O. C. Rose. 1997. Three ways of assessing metapopulation structure in the butterfly Plebejus argus. Ecological Entomology 22:283-293.
Loken, A. 1961. Bombus consobrinus Dahlb., an oligolectic bumble bee (Hymenoptera: Apidae). Proceedings of the XIth International Congress of Entomology. 1:598-603.
Lynch, M., J. Conery, and R. Bürger. 1995. Mutation accumulation and the extinction of small populations. American Naturalist 146:489-518.
Marlin, J. C., and W. E. LaBerge. 2001. The native bee fauna of Carlinville, Illinois, revisited after 75 years: a case for persistence. Conservation Ecology 5(1):9. [online] URL: http://www.consecol.org/vol5/iss1/art9
Maruyama, T., and M. Kimura. 1980. Genetic variation and effective population size when local extinction and recolonization of subpopulations are frequent. Proceedings of the National Academy of Sciences (USA) 77:6710-6714.
Matheson, A., S. L. Buchmann, C. O’Toole, P. Westrich, and I. H. Williams, editors. 1996. The conservation of bees. Academic Press, London, UK.
McCauley, D. E. 1991. The effect of host plant patch size variation on the population structure of a specialist herbivore insect, Tetraopes tetraophthalmus. Evolution 45:1675-1684.
McCauley, D. E. 1993. Genetic consequences of extinction and recolonization in fragmented habitats. Pages 217-233 in P. M. Kareiva, J. G. Kingsolver, and R. B. Huey, editors. Biotic interactions and global change. Sinauer, Sunderland, Massachusetts, USA.
Meglecz, E., K. Pescenye, Z. Varga, and M. Solignac. 1998. Comparison of differentiation pattern at allozyme and microsatellite loci in Parnassius mnemosyne (Lepidoptera) populations. Hereditas 128:95-103.
Merola, M. 1994. A reassessment of homozygosity and the case for inbreeding depression in the cheetah (Acinonyx jubatus): implications for conservation. Conservation Biology 8:961-971.
Metcalf, R. A., J. C. Marlin, and G. S. Whitt. 1975. Low levels of genetic heterozygosity in Hymenoptera. Nature 257:792-794.
Michener, C. D. 1966. Interactions among workers from different colonies of sweat bees. Animal Behaviour 14:126-129.
Michener, C. D. 1974. The social behavior of the bees: a comparative study. Belknap Press of Harvard University Press, Cambridge, Massachusetts, USA.
Mills, L. S., and F. W. Allendorf. 1996. The one-migrant-per-generation rule in conservation and management. Conservation Biology 10:1509-1518.
Mitton, J. B. 1993. Theory and data pertinent to the relationship between heterozygosity and fitness. Pages 17-41 in N. Wilmsen Thornhill, editor. The natural history of Inbreeding and outbreeding: theoretical and empirical perspectives. University of Chicago Press, Chicago, Illinois, USA.
Moritz, C. 1994. Defining evolutionarily significant units for conservation. Trends in Ecology and Evolution 9:373-375.
Muller, C. B. and P. Schmidt-Hempel. 1992. Correlates of reproductive success among field colonies of Bombus lucorum: the importance of growth and parasites. Ecological Entomology 17:343-353.
Nagylaki, I. 1981. The inbreeding effective population number and the expected heterozygosity for an X-linked locus. Genetics 47:731-737.
Neff, J. L., and B. B. Simpson. 1993. Bees, pollination systems and plant diversity. Pages 143-167 in J. LaSalle and I. D. Gauld, editors. Hymenoptera and biodiversity. The Natural History Museum. C. A. B. International, Wallingford Oxon, UK.
Nei, M., and A. K. Roychoudhury. 1974. Sampling variances of heterozygosity and genetic distance. Genetics 76:379-390.
O'Brien, S. J., D. E. Wildt, D. Goldman, C. R. Meril, and M. Bush. 1983. The cheetah is depauperate in genetic variation. Science 221:459-461.
Owen, R. E. 1985a. The opportunity for polymorphism and genic variation in social Hymenoptera with worker-produced males. Heredity 54:25-36.
Owen, R. E. 1985b. Difficulties with the interpretation of patterns of genetic variation in the eusocial Hymenoptera. Evolution 39:201-205.
Owen, R. E. 1993. Genetics of parasitic Hymenoptera. Pages 69-89 in S. K. Narang, A. C. Bartlett, and R. M. Faust, editors. Applications of genetics to arthropods of biological control significance. C.R.C. Press, Boca Raton, Florida, USA.
Owen, R. E., and L. Packer. 1994. Estimation of the proportion of diploid males in populations of Hymenoptera. Heredity 72:219-227.
Owen, R. E., F. H. Rodd, and R. C. Plowright.1980. Sex ratios in bumble bee colonies:
Complications due to orphaning? Behavioral Ecology and Sociobiology 7:287-291.
Packer, L. 1986. The social organisation of Halictus ligatus (Hymenoptera; Halictidae) in southern Ontario. Canadian Journal of Zoology 64:2317-2324.
Packer, L. 1992. The social organisation of Lasioglossum (Dialictus) laevissimum in Southern Alberta. Canadian Journal of Zoology 70:1767-1774.
Packer, L. 1993. Multiple foundress associations in sweat bees. Pages 215-233 in L. Keller, editor. Queen number and sociality in insects. Oxford University Press, Oxford, UK.
Packer, L. 1994. The extirpation of the Karner Blue butterfly in Ontario. Pages 143-152 in D. Andow, R. Baker, and C. Lane, editors. The Karner blue butterfly: a symbol of a vanishing landscape. University of Minnesota Press, St. Paul, Minnesota, USA.
Packer, L., A. Dzinas, K. Strickler, and V. Scott.1995. Genetic differentiation between two host "races" and two species of cleptoparasitic bees and their hosts. Biochemical Genetics 33:97-109.
Packer, L., and R. E. Owen. 1989. Isozyme variation in Halictus rubicundus: a primitively social bee (Hymenoptera: Halictidae). Canadian Entomologist 121: 1049-1058.
Packer, L., and R. E. Owen. 1990. Allozyme variation, linkage disequilibrium and diploid male production in a primitively social bee Augochlorella striata (Hymenoptera: Halictidae). Heredity 65:241-248.
Packer, L., and R. E. Owen. 1992. Variable enzyme systems in the Hymenoptera. Biochemical Systematics and Ecology 20:1-7.
Packer, L., and R. E. Owen. 1994. Relatedness and sex ratio in a primitively eusocial halictine bee. Behavioral Ecology and Sociobiology 34:1-10.
Packer, L., A. Porsa, C. Plateaux-Quénu, and L. Plateaux. 1999. A cryptic species allied to Evylaeus villosulus (Kirby) (Hymenoptera: Halictidae). Annales de la Société Entomologique de France 35:165-171.
Packer, L., and J. Taylor. 1997. How many cryptic species are there? An application
of the phylogenetic species concept to genetic data for some comparatively well known bee species. Canadian Entomologist 129:587-594.
Packer, L., J. Taylor, D. Savignano, C. Bleser, C. Lane, and L. Sommers. 1998. Population biology of an endangered butterfly, Lycaeides melissa samuelis (Lepidoptera; Lycaenidae): Genetic variation, gene flow and taxonomic status. Canadian Journal of Zoology 76:320-329.
Page, R. E. Jr. 1981. Protandrous reproduction in honey bees (Apis mellifera L.Environmental Entomology 10:359-362.
Pamilo, P., and R. H. Crozier. 1981. Genic variation in male haploids under deterministic selection. Genetics 98:199-214.
Pamilo, P., S. Varvio-Aho, and A. Pekkarinen. 1978. Low enzyme gene variability in Hymenoptera as a consequence of haplodiploidy. Hereditas 88:93-99.
Peterson, M. A., and R. F. Denno. 1998a. Life history strategies and the genetic
structure of phytophagous insect populations. Pages 263-322 in S. Mopper and S. Strauss, editors. Genetic structure and local adaptation in natural insect populations: effects of ecology, life history and behavior. Chapman & Hall, New York, New York, USA.
Peterson, M. A., and R. F. Denno. 1998b. The influence of dispersal and diet breadth on patterns of genetic isolation by distance in phytophagous insects. American Naturalist 152:428-446.
Petters, R. M., and R. V. Mettus. 1980. Decreased diploid male viability in the parasitic wasp Bracon hebetor. Journal of Heredity 71:353-356.
Plowright, R. C., and M. J. Pallett. 1979. Worker-male conflict and inbreeding in bumble bees (Hymenoptera: Apidae). Canadian Entomologist 111:289-294.
Porter, A. H., and H. Geiger. 1995. Limitations to the inferences of gene flow at regional geographic scales- an example from the Pieris napi group (Lepidoptera: Pieridae) in Europe. Biological Journal of the Linnaean Society 54:329-348.
Pullin, A. S. 1995. Ecology and conservation of butterflies. Chapman and Hall, London, UK.
Quattro, J. M., and R. C. Vrijenhoek. 1989. Fitness differences among remnant populations of the endangered Sonoran topminnow. Science 245:976-978.
Ralls, K., and J. D. Ballou. 1986. Captive breeding programs for populations with a small number of founders. Trends in Ecology and Evolution 1:19-22.
Reeve, H. K., J. S. Reeve, and D. W. Pfennig. 1985. Eusociality and genetic variability: a re-evaluation. Evolution 39:200-201.
Richards, M. H., J. Seger, and L. Packer. 1995. Unexpected patterns of parentage and relatedness in a primitively eusocial bee. Nature 373:239-241.
Ridley, M. 1983. The explanation of organic diversity: the comparative method and adaptations for mating. Oxford University Press, Oxford, UK.
Roderick, G. K. 1996. Geographic structure of insect populations: Gene flow, phylogeography, and their uses. Annual Review of Entomology 41:325-352.
Ross, K. G., D. Shoemaker, M. J. B. Krieger, C. J. Deheer, and L. I. Keller. 1999. Assessing genetic structure with multiple classes of molecular markers: A case study involving the introduced fire ant Solenopsis invicta. Molecular Biology and Evolution 16:525-543.
Roubik, D. W., L. A. Weigt, and M. A. Bonilla. 1996. Populations genetics, diploid males, and limits to social evolution of Euglossine bees. Evolution 50:931-935.
Roubik, D. W. 2001. Ups and downs in pollinator populations: when is there a decline? Conservation Ecology 5(1):2. [online] URL: http://www.consecol.org/vol5/iss1/art2
Saccheri, I., M. Kuussari, M. Kankare, P. Vikman, W. Fortelius, and I. Hanski. 1998. Inbreeding and extinction in a butterfly metapopulation. Nature 392:491-494.
Schmidt, J. O., and P. J. Schmidt. 1986. A nesting aggregation of Lasioglossum kinabaluense Michener in Borneo (Hymenoptera: Halictidae). Journal of the Kansas
Entomological Society 59:672-674.
Seeley, T. D. 1985. Honeybee ecology: study of adaptation in social life. Princeton
University Press, Princeton, New Jersey, USA.
Seufert, W., and N. Grosser. 1996. A population ecological study of Chazara briseis (Lepidoptera, Sayrinae). Pages 268-274 in J. Settele, C. R. Margules, P. Poschlod, and K. Henle, editors. Species survival in fragmented landscapes. Kluwer, Amsterdam, The Netherlands.
Shoemaker, D. D., J. T. Costa, and K. G. Ross. 1993. Estimates of heterozygosity in two social insects using a large number of electrophoretic markers. Heredity 69:573-582.
Singh, R. S., and L. R. Rhomberg. 1987. A comprehensive study of genic variation in natural populations of Drosophila melanogaster. Genetics 115:313-322.
Slatkin, M. 1985. Gene flow in natural populations. Annual Review of Ecology and Systematics 16:393-430.
Slatkin, M. 1993. Isolation by distance in equilibrium and non-equilibrium populations. Evolution 47:264-279.
Slatkin, M. 1994. Gene flow and populations structure. Pages 3-17 in L. A. Real, editor. Ecological genetics. Princeton University Press, Princeton, New Jersey, USA.
Slatkin, M., and N. H. Barton. 1989. A comparison of three indirect methods for estimating average levels of gene flow. Evolution 43:1349-1368.
Smith, S. G., and D. R. Wallace. 1971. Allelic sex determination in a lower hymenopteran, Neodiprion nigroscutum Midd. Canadian Journal of Genetics and Cytology 13:617-621.
Sork, V. L., D. Campbell, R. Dyer, J. Fernandez, J. Nason, R. Petit, P. Smouse, and E. Steinberg. 1998. Proceedings from a workshop on gene flow in fragmented, managed, and continuous populations. National Center for Ecological Analysis and Synthesis. [available online] URL: http://www.nceas.ucsb.edu/nceas-web/projects/2057/nceas-paper2/
Soulé, M. 1976. Allozyme variation: its determinants in space and time. Pages 60-77 in F. J. Ayala, editor. Molecular evolution. Sinauer, Sunderland, Massachusetts, USA.
Soulé, M. E. 1980. Thresholds for survival; maintaining fitness and evolutionary potential. Pages 151-169 in M. E. Soulé and B. A. Wilcox, editors. Conservation biology; an evolutionary-ecological approach. Sinauer, Sunderland, Massachusetts, USA.
Swofford, D. L., and R. B. Selander. 1989. BIOSYS-1: a computer program for the analysis of allelic variation in population genetics and biochemical systematics. Illinois Natural History Survey, Urbana, Illinois, USA.
Thomson, J. D. 2001. Using pollination deficits to infer pollinator declines: Can theory guide us? Conservation Ecology 5(1):6. [online] URL: http://www.consecol.org/vol5/iss1/art6
Unruh, T. R., and R. H. Messing. 1993. Intraspecific biodiversity in Hymenoptera:
Implications for conservation and biological control. Pages 27-52 in J. LaSalle and I. D. Gauld, editors. Hymenoptera and biodiversity. The Natural History
Museum. C. A. B. International, Wallingford Oxon, UK.
Veith, M., B. Johannesen, D. Nicklas-görgen, U. S. Schmeller, and A. Seitz. 1996. Genetics of insect populations in fragmented landscapes - a comparison of species and habitats. Pages 344-355 in J. Settele, C. R. Margules, P.Poschlod, and K. Henle, editors. Species survival in fragmented landscapes. Kluwer, Amsterdam, The Netherlands.
Waller, D. M., D. M. O'Malley, and S. C. Gawler. 1987. Genetic variation in the extreme endemic Pedicularis furbishiae (Scrophulariaceae). Conservation Biology 1:335-340.
Wcislo, W. T. 1987. The role of learning in the mating biology of a sweatbee, Lasioglossum zephyrum (Hymenoptera: Halictidae). Behavioral Ecology and Sociobiology 20:179-185.
Wcislo, W. T. 1997. Are behavioral classifications blinders to studying natural variation? Pages 8-13 in J. C. Choe and B. J. Crespi, editors. Social behavior in insects and arachnids. Cambridge University Press, Cambridge, UK.
Weir, B. S., and C. C. Cockerham. 1984. Estimating F statistics for the analysis
of population structure. Evolution 38:1358-1370.
Werren, J. H. 1983. Sex ratio evolution under local mate competition in a parasitic wasp. Evolution 37:116-124.
Werren, J. H. 1993. The evolution of inbreeding in haplodiploid organisms. Pages 42-59 in N. Wilmsen Thornhill, editor. The natural history of inbreeding and outbreeding: theoretical and empirical perspectives. University of Chicago Press, Chicago, Illinois, USA.
Whiting, P. W. 1943. Multiple alleles in complementary sex determination of Habrobracon. Genetics 28:365-382.
Whitlock, M. C., and D. E. McCauley. 1990. Some population genetic consequences of colony formation and extinction: genetic correlations within founding groups. Evolution 44:1717-1724.
Widmer, A., and P. Schmid-Hempel. 1999. The population genetic structure of a large temperate pollinator species, Bombus pascuorum (Scopoli) (Hymenoptera: Apidae). Molecular Ecology 8:387-398.
Widmer, A., P. Schmid-Hempel, A. Estoup, and A. Scholl. 1998. Population genetic structure and colonization history of Bombus terrestris s.I. (Hymenoptera: Apidae) from the Canary Islands and Madeira. Heredity 81:563-572.
Woyke, J. 1976. Population genetic studies on sex alleles in the honeybee using the example of the Kangaroo island bee sanctuary. Journal of Apicultural Research 15:105-123.
Wright, S. 1931. Evolution in Mendelian populations. Genetics 16:97-259.
Wright, S. 1951. The genetical structure of populations. Annals of Eugenics 15:323-354.
Yanega, D. 1990. Philopatry and nest founding in a primitively social bee, Halictus rubicundus. Behavioral Ecology and Sociobiology 27:37-42.
Address of Correspondent:
Laurence Packer
Department of Biology
York University
4700 Keele St.
Toronto, Ontario
Canada, M3J 1P3
Phone: (416) 736-2100 Ext. 22663
Fax: (416) 736-5989
bugsrus@yorku.ca