|
|
|
Copyright © 2000 by The Resilience Alliance
The following is the established format for referencing this article:
Baumann, M. 2000. On nature, models, and simplicity. Conservation Ecology 4(2): r4. [online] URL: http://www.consecol.org/vol4/iss2/resp4/
Response to C. S. (Buzz) Holling 2000. "Two Cultures of Ecology" On Nature, Models, and Simplicity Michael Baumann
University of British Columbia and ananature.com Scientific Services
- Introduction
- Life, the Universe, and Everything
- Life, Mathematics, and Computer Programs
- The Need for Simplicity
- Responses to this Article
- Acknowledgments
- Literature Cited
KEY WORDS: complexity, epistemology, modeling, simplicity.
Published: September 21, 2000
First, let me apologize for possibly taking too broad a view in this brief discussion, but unfortunately, as I will show, nature is not reasonably separable into thematic chapters. Because each of the topics I am trying to embrace deserves at least the volume of a major treatise, if not its own library, my analysis has to be somewhat incomplete, but comes to full circle nevertheless.
In his inaugural editorial to Conservation Ecology, Holling distinguishes between the analytical and the integrative culture in ecology (Holling 1998). Although the advantages and shortcomings of the two approaches are evident simply from comparison of their attributes (Holling 1998: Table 1), I briefly want to address the cardinal assumptions associated with the main methodology in integrative ecology, i.e., mathematical modeling. The following is in the spirit that “exposure and castigation of error does not propel science forward, [but] it may clear a number of obstacles from its path.” (Medawar 1969).
Ecologists study life and life is complex. So what makes an organism alive or remain in that state, from an ecologist’s point of view rather than from the physicists’ “dissipative structure” concept (Nicolis and Prigogine 1977)? An individual’s instantaneous biological state st, a vector, is determined by local and current interactions between the individual and its biotic and abiotic environment such that:
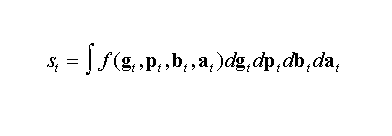 (1)
(1)
Here, st(with elements such as current velocity, blood glucose concentration, level of alertness, ontogenetically learned contents), is the integral over the interactions f that occur between the individual’s genetic state vector gt (e.g., biochemical, developmental, and cognitive predispositions and capacities), its phenotypic state vector pt (e.g., current physiological, morphological, and behavioral realizations), and the biotic and abiotic environmental state vectors, bt (e.g., current velocity of closest predator, developmental stage of closest competitor and its spatial position with respect to weakest prey individual within reactive distance), and at (e.g., current local temperature and visibility field, landscape topography), respectively.
As indicated by the index, gt, pt, bt, and at are all realizations at a particular time t, and are themselves determined by previous interactions F such that:
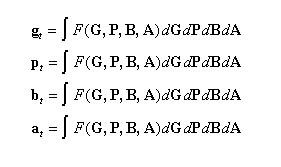 (2)
(2)
where G, P, B, and A represent continuous high-dimensional, temporal fields in genetic, phenotypic, biotic, and abiotic environmental hyperspace. (Note that changes in g, p, b, and a will involve different time scales: e.g., individually learnable concepts, as included in p, will change faster than an organism’s overall capacity to learn, represented in g.)
An individual’s or an organism’s ability to survive and reproduce is determined by learning about its biotic (B) and abiotic environment (A) at the physiological and/or neurological (P) as well as the genetic level (G). For experience to be useful, the complexities of the real world have to be simplified. Cause and effect as encountered in specific situations are idealized and compressed in an abstraction process resulting in a general model of causation in the real world. Here is an example at the cognitive level. An antelope (gt, pt), seeing a leopard’s tail in the grass (both elements of bt), will link the tail to a whole leopard (element of bt) behind the bush (element of bt and at), and will deduce the leopard’s intentions (element of bt) from the fact that it is hiding (element of bt). If one is concerned with survival and reproduction, any other model in the antelope’s mind is rather unwise, a deadly process error, so to speak.
Obviously, living nature is dynamic, and the rational way “to cope with the uncertain, the unexpected, the unknown” (Holling 1976) is to test and revise one’s models by conservative trial-and-error learning, which “should not, ideally, destroy the [observer or] experimenter” (Holling 1976). To my understanding, this must be true for all organisms. However, on Earth only humans seem to have attained the ability to explicitly formalize problems before choosing among alternative actions with uncertain outcomes. In hope of understanding and predicting nature, humans use verbal, graphical, statistical (descriptive), and (most sophisticated) mathematical (mechanistic) models.
As I have just tried to show, the complexity of living nature does not easily lend itself to investigation, and has consequently lead to the development of “two cultures in ecology” (Holling 1998): analysts and synthesists. Although the analyst school obviously is very successful in measuring large treatment effects among populations with tiny variances, by definition, only the approach of the synthesists enables us to study ecological complexity.
The research tools of choice in integrative ecology are mathematical models, mostly in the form of systems of difference or differential equations. The power of mathematics lies in the aggregation of similar entities into a larger group (that’s why it is so successful in physics and chemistry). Consequently, the price mathematical modelers have to pay in order to use mathematics to analyze ecological problems is accepting the three cardinal assumptions of ecological
modeling:
- There is no ontogenetic or genetic variation among individuals of aggregated groups, i.e., each individual will affect its biotic and abiotic environment in exactly the same way, and will be affected by abiotic and biotic factors in exactly the same way.
- There is no ontogenetic or genetic variability, i.e., individuals remain unchanged and organisms are immutable over time periods relevant to ecology.
- There is no interaction between different hierarchical levels of biological organization.
Unfortunately, variability in space and time, and interactions between different hierarchical levels, e.g., genes, organisms and environment (Lewontin 2000), are the three elements that distinguish the living from the dead, biology from physics. Although the first two elements can partly, although only rudimentarily, be accommodated in ecological models, e.g., Leslie matrix (Leslie 1945) and optimization models (Mangel and Clark 1988), the third element is extremely difficult to deal with formally, to the point that its effects are completely unknown: “Parts and wholes evolve in consequence of their relationship, and the relationship itself evolves” (Levins and Lewontin 1985). The parts build up the whole, which in turn forms the context in which the contents exist. Perhaps, biological phenomena cannot be accounted for by mathematical shortcuts, and even inanimate nature might be fundamentally irreducible (Wolfram 2001).
However, there has been a methodological - to use the dreadful expression - “paradigm shift” (Kuhn 1970) in quantitative ecology in the 1990s. Advances in computer technology have enabled ecologists to replace the extraction and assembly approach of the top-down modeling paradigm as required by mathematics (M. Baumann, unpublished manuscript) with individual-based modeling (Langton 1989, Judson 1994). The individual- or agent-based approach allows for a relaxation of all three cardinal assumptions of ecological modeling, but has very often only resulted in the design of computer games not dissimilar to John Conway’s game of “Life” cellular automaton framework (Gardner 1970).
Frequently, the output patterns of such games are similar to patterns that are observed in nature, but are generated by rules that are only vaguely or not at all related to natural behavior and processes. This fallacy, that similar effects have similar causes, has been called “reminiscence syndrome” (Horgan 1995), and has been described epistemologically in the Hypothesis of the First Cause (Riedl 1984). In any case, the general conclusion from most individual-based computer models can be summarized as: Simple rules applied locally and in parallel by a large number of autonomous agents result in complicated global spatiotemporal patterns.
The crux with traditional mathematical models is that we do not know, in principle, how well they capture essential properties of biological systems. Thus, Levin et al. (1997) propose a modern research agenda in conservation ecology: “extensive simulation of detailed [i.e., agent-based] models, comparison with aggregated models, and the development of rules for relating these models to one another and for providing simplified descriptions.” This translates into using the individual-based computer emulations as laboratory worlds that are free of the uncertainties and contingencies associated with data from the natural system (Oreskes et al. 1994) to weed out bad mathematical models and find appropriate shortcuts in understanding natural systems.
It can be argued that simplicity is necessary for methodological reasons. By starting out simple and letting progress in understanding of the modeled system guide enlargement of the model, one can be sure to identify “unnecessary” details that have insignificant effects on the model system (but may well be relevant to the modeled system). Yet, how much “unnecessary” detail should Ockham’s Razor be allowed to shave off of reality in order to produce “the laws of nature”? Simple-minded comparison of model results with observational data will not give any answers either. First, “what we call data are inference-laden signifiers of natural phenomena to which we have incomplete access” (Oreskes et al. 1994); and second, nature and models are not unique: many mechanisms may produce the same patterns.
Maybe Eugene Wigner’s two miracles are not so miraculous after all: “the miracle of the existence of laws of nature and the miracle of the capacity of the human mind to divine them” (Chandrasekhar 1990). There is a tangible possibility that “Those problems that yield to the attack are pursued most vigorously, precisely because the method works there” (Levins and Lewontin 1985)? In fact, it should surprise us if nature were simple enough to be understood by the human mind, yet complex enough to reveal herself only through our most sophisticated intellectual tools.
There is something fundamental here. Just as the antelope’s cognitive apparatus has been shaped by past selection events (after all, why should bushes not have leopard tails?), the human mind is a consequence of evolutionary conflicts and constraints. Considering that “survive and reproduce” is a fairly simple rule, understanding of complex adaptive systems such as ecological and economic systems may lie beyond the scope of past selection pressures (Riedl 1981, McIntyre 1998). In a third revolution, after the Copernican and Darwinian (Gott 1993), we might want to shed the last remaining pretension and consider the possibility that our capacity for understanding (gt, pt) and our learned contents (st) may well be insufficient to explain nature.
But how wise is it to admit fundamental ignorance in today’s institutional(ized) science regime?
Responses to this article are invited. If accepted for publication, your response will be hyperlinked to the article. To submit a comment, follow this link. To read comments already accepted, follow this link.
No thanks would be too much for Sol Hadden. This work was financed by the Austrian Science Fund while the author was a Schrödinger Fellow at the Institute for Resources and Environment, University of British Columbia.
Chandrasekhar, S. 1990. Science and scientific attitudes. Nature 344:285-286.
Gardner, M. 1970. Mathematical games. Scientific American 223:120-123.
Gott, J. R. 1993. Implications of the Copernican principle for our future prospects. Nature 363:315-319.
Holling, C. S. 1976. Myths of ecology and energy. Pages 34-49. Future strategies of energy development: A question of scale. Oak Ridge Associated Universities, Oak Ridge, Tennesee, USA.
Holling, C. S. 1998. Two cultures of ecology. Conservation Ecology 2:4. [online] URL: http://www.consecol.org/Journal/vol2/iss2/art4.
Horgan, J. 1995. From complexity to perplexity. Scientific American 272:104-109.
Judson, O. P. 1994. The rise of the individual-based model in ecology. Trends in Ecology and Evolution 9:9-14.
Kuhn, T. S. 1970. The structure of scientific revolutions. Unviersity of Chicago Press, Chicago, Illinois, USA.
Langton, C. G. 1989. Artificial life. Pages 1-47 in C. G. Langton, editor. Artificial life. Addison-Wesley, Redwood City, California, USA.
Leslie, P. H. 1945. On the use of matrices in certain population mathematics. Biometrika 33:183-212.
Levin, S. A., B. Grenfell, A. Hastings, and A. S. Perelson. 1997. Mathematical and computational challenges in population and ecosystems science. Science 275:334-343.
Levins, R., and R. Lewontin. 1985. The dialectical biologist. Harvard University Press, Cambridge, Massachusetts, USA.
Lewontin, R. C. 2000. The triple helix: gene, organism, and environment. Harvard University Press, Cambridge, Massachusetts, USA.
Mangel, M., and C. W. Clark. 1988. Dynamic modeling in behavioural ecology. Princeton University Press, Princeton, New Jersey, USA.
McIntyre, L. 1998. Complexity: a philosopher’s reflections. Complexity 3(6):26-32.
Medawar, P. B. 1969. Induction and intuition in scientific thought. American Philosophical Society, Philadelphia, Pennsylvania, USA.
Nicolis, G., and I. Prigogine. 1977. Self-organization in nonequilibrium systems: From dissipative structures to order through fluctuations. John Wiley, New York, New York, USA.
Oreskes, N., K. Shrader-Frechette, and K. Belitz. 1994. Verification, validation, and confirmation of numerical models in the earth sciences. Science 263:641-646.
Riedl, R. 1981. Biologie der Erkenntnis. Verlag Paul Parey, Berlin, Germany.
Riedl, R. 1984. Biology of knowledge. John Wiley, Chichester, UK.
Wolfram, S. 2001. A new kind of science. Wolfram Media Inc., Champaign, Illinois, USA, in press.
Address of Correspondent:
Michael Baumann
Institute for Resources and Environment
University of British Columbia
2206 East Mall
Vancouver, British Columbia
Canada V6T 1Z3
Phone: (604) 822-0027
baumann@interchange.ubc.ca