|
|
|
Copyright © 2000 by The Resilience Alliance
The following is the established format for referencing this article:
Walters, C., J. Korman, L. E. Stevens, and B. Gold. 2000. Ecosystem modeling for evaluation of adaptive management policies in the Grand Canyon. Conservation Ecology 4(2): 1. [online] URL: http://www.consecol.org/vol4/iss2/art1/
A version of this article in which text, figures, tables, and appendices are separate files may be found by following this link.
Synthesis Ecosystem Modeling for Evaluation of Adaptive Management Policies in the Grand Canyon Carl Walters1, Josh Korman2, Lawrence E. Stevens3, and Barry Gold4
1University of British Columbia; 2Ecometric Research Inc.; 3Stevens Ecological Consulting; 4Grand Canyon Monitoring and Research Center
- Abstract
- Introduction
- Approach to Modeling Multiscale Policy and Ecosystem Dynamics
- Key Submodels and Comparisons of Model Predictions to Data
- Physical Submodel
- Policy Predictions and Uncertainties
- Conclusion: Experimental Management Options for the Grand Canyon
- Responses to this Article
- Acknowledgments
- Literature Cited
- Appendix 1
- Appendix 2
- Appendix 3
- Appendix 4
- Appendix 5
- Appendix 6
- Appendix 7
- Appendix 8
- Appendix 9
- Appendix 10
- Appendix 11
- Appendix 12
- Appendix 13
- Appendix 14
- Appendix 15
- Appendix 16
- Erratum (added 3 April 2003)
An Adaptive Environmental Assessment and Management workshop process was used to assist Grand Canyon scientists and managers in developing conceptual and simulation models for the Colorado ecosystem affected by Glen Canyon Dam. This model examines ecosystem variables and processes at multiple scales in space and time, ranging from feet and hours for benthic algal response to diurnal flow changes, to reaches and decades for sediment storage and dynamics of long-lived native fish species. Its aim is to help screen policy options ranging from changes in hourly variation in flow allowed from Glen Canyon Dam, to major structural changes for restoration of more natural temperature regimes. It appears that we can make fairly accurate predictions about some components of ecosystem response to policy change (e.g., autochthonous primary production, insect communities, riparian vegetation, rainbow trout population), but we are moderately or grossly uncertain about others (e.g., long-term sediment storage, response of native and non-native fishes to physical habitat restoration). Further, we do not believe that existing monitoring programs are adequate to detect responses of native fishes or vegetation to anything short of gross habitat changes. Some experimental manipulations (such as controlled floods for beach/habitat-building) should proceed, but most should await development of better monitoring programs and sound temporal baseline information from those programs.
KEY WORDS: adaptive management, aquatic primary productivity, Colorado River, dam, ecosystem models, Grand Canyon, habitat restoration, hydrology, insect productivity, native fishes, riparian ecosystems, sediment budget.
Published: July 24, 2000
The Colorado River ecosystem between Glen Canyon Dam (GCD) and upper Lake Mead, Arizona, USA provides a unique opportunity to test various ideas about river management and the use of adaptive management experiments to help resolve scientific uncertainties about best management practices (Bureau of Reclamation 1995, Adler 1996, NRC 1996, Collier et al. 1997, Schmidt et al. 1998). The river is bounded upstream by Glen Canyon Dam, where water regulation for hydropower production results in delivery of cold, clear, and relatively steady flows into the upper canyon (Fig. 1). The river ecosystem ends 250 miles (402 km) downstream at Lake Mead. Natural flows (prior to 1963) were violently seasonal, extremely turbid, and highly variable in temperature. Regulated flows have permitted the development of a productive aquatic community in the upper canyon, sustaining a spectacular rainbow trout (Oncorhynchus myksiss) fishery and seasonally dense avifauna populations, including Bald Eagle (Haliaeetus leucocephalus), other waterbirds, Peregrine Falcon (Falco peregrinus anatum), and endangered neotropical migrant songbirds. As water moves through the Grand Canyon, tributary sediment inputs result in progressive increases in turbidity, shutting down the primary production system and resulting in much lower densities of aquatic invertebrates, fishes, and birds. Endangered native species such as humpback chub (Gila cypha) and flannelmouth sucker (Catostomus latipinnis) now use mainly warm tributary and backwater habitats, and are assumed to have declined greatly in the face of cold mainstem flows and impacts of exotic predators and competitors, including rainbow and brown trout (Salmo trutta), channel catfish (Ictalurus punctatus), carp (Cyprinus carpio), fathead minnows (Pimephales promelas), and redside shiners (Richardsonius balteatus), that have been introduced into the system.
Since the early 1980s, the U.S. Bureau of Reclamation (BOR) has overseen intensive scientific studies conducted by its staff, the U.S. Geological Survey, U.S. National Park Service, U.S. Fish and Wildlife Service (FWS), and the Arizona Fish and Game Department to document spatial and temporal changes in the Colorado River ecosystem. Based on an Environmental Impact Statement completed in 1995 (GCD-EIS; BOR 1995) and a Record of Decision (1996), the managing agencies adopted an “Adaptive Management Program” to seek best strategies for balancing potentially conflicting goals of water use, recreation, and protection of native species (Schaefer 1997). A first test of this program, and demonstration of commitment to an adaptive management approach, was the widely publicized “beach/habitat-building flow” (BHBF) experiment in 1996. One of the primary objectives of the controlled flood was to determine if sand could be moved from the main river channel onto lateral deposits used for camping, and reverse successional impacts on the productivity of backwater/slough habitats (Anonymous 1997, Collier et al. 1997, Webb et al. 1999). Although it was not widely publicized as an experiment, there was actually an even more dramatic policy change in 1991 based on scientific findings as of that time: the introduction of “Interim flows” (IF) and the GCD-EIS preferred alternative, “modified low-fluctuating flows” (MLFF). Prior to 1991, Glen Canyon Dam flows were characterized by wide hourly variation, with nighttime releases as low as 1000 cubic feet per second (1000 cfs = 28 m3/s) and daytime releases > 31,000 cfs (878 m3/s) to maximize peaking-power revenues. Diurnal low flows prevented the development of benthic communities over much of the upper river bottom, and severely limited reproductive success of at least rainbow trout (exposing redds to drying, and forcing juveniles to move into areas of high predation risk). Aquatic productivity, or at least the area of shallow river bottom that can support algal and benthic insect community development, has responded dramatically to reduced diurnal variation under the IF and MLFF policies. The IF and MLFF flow policies have apparently reduced the transport of sand from the main channel to higher elevation eddy deposits, resulting in net erosion of camping beaches prized by whitewater rafters. High flows, such as the 1996 experimental flood, were recognized as necessary to deposit sand at higher stage elevations and rebuild sand bars (BOR 1995).
By 1997, it was recognized that development of explicit dynamic simulation models of the Colorado River ecosystem might be helpful in future adaptive management planning. Proponents of adaptive management have long emphasized the importance of such modeling (Holling 1978, Walters 1986), not to permit detailed quantitative predictions about policy options, but rather to serve at least two other key purposes. First, we have argued that just trying to build an explicit numerical model requires a clear statement of what is known and what is assumed, which helps to expose broad gaps in data and understanding that are easily overlooked in verbal and qualitative assessments. As we tell participants in introductions to Adaptive Environmental Assessment and Management (AEAM) workshops, things you can get away with on paper have a nasty way of coming back to haunt you when you try to represent them clearly enough that a computer can reproduce the steps in your reasoning. Second, we have found that even crude models can help “screen” policy options and eliminate those that are simply too small in scale to be important, or would be risky, given uncertainty about directions of response in key policy indicators.
Most applications of dynamic modeling as a tool for adaptive management planning have not been obviously successful (Walters 1997), but there were some special reasons for optimism in the case of the Colorado River ecosystem in Grand Canyon: (1) a history of commitment to and excitement about the value of large-scale management experiments; (2) a wealth of data on system component and process responses to the strong spatial and temporal gradients created by past management decisions; and (3) frustration among stakeholders about the possibility that future management policies might be based on myopic concerns about particular factors, such as sandbar building or protection of particular endangered species, rather than on a reasoned analysis of conflicts and trade-offs.
This paper documents the initial development of GCM, an ecosystem model that we developed in 1998, using AEAM workshops with participation of over 40 scientists and managers from the Colorado River ecosystem. We review findings from the model to date about monitoring, research, and screening of future management experiments. Model development has generated important insights about research and monitoring design for future ecosystem management, and about the dangers of basing ecosystem management policies primarily on concepts of physical habitat restoration. Also, GCM may be a valuable instructional tool for researchers and students interested in river ecosystem management; it is available to download from the Grand Canyon Monitoring and Research Center web site at http://130.118.161.89/gcmrc/conceptu.htm. [ERRATUM: The link to the Grand Canyon Monitoring and Research Center web site has been changed to: http://www.gcmrc.gov/CM/CM.htm]
Development of GCM proceeded in several steps. First, a “scoping workshop” with key Grand Canyon stakeholders led to the definition of a set of basic submodels that a useful ecosystem simulation would have to contain (Fig. 2). These submodels range from a “driving” submodel to specify alternate Glen Canyon Dam (GCD) discharge and temperature release scenarios, through benthic primary and invertebrate production submodels, to a multispecies population dynamics accounting submodel for a fairly large set of indicator vertebrate species, as well as an accounting submodel for economic/recreational indicators ranging from power production values to whitewater rafting and trout fishing.
A critical step in the scoping workshop was to define the type and range of policy options to be represented in the model. This was important not only to help us design a model capable of responding usefully to particular policy questions, but also to help define the types and space-time resolution of dynamic state variables needed for the calculations. Policy options defined at this step included:
- alternative diurnal patterns of dam releases (e.g., maximum and minimum daily flows, hourly
ramping rates between flow extremes, maximum daily flow changes);
- alternative seasonal schedules of dam releases, particularly schedules that more closely mimic the natural seasonal hydrograph (e.g., seasonally adjusted steady flows);
- beach/habitat-building pulse flows (managed floods) of varying magnitude, duration, frequency, and seasonal timing;
- restoration of more natural thermal regimes below GCD by construction of a selective withdrawal release structure at GCD;
- restoration of more natural sediment/turbidity regimes below GCD by transport of sediments from above Lake Powell;
- direct control of selected non-native plant and fish species;
- changes in whitewater rafting access and allocation among different user groups (e.g., reducing the total number of river trips, and increasing allocation for private trips to reduce demand on camping beaches).
In addition to these potential policy changes, we felt that it was important for the model be able to at least roughly represent the effects of removing GCD completely (pre-impoundment (1963) river), as a test for whether model parameter values would imply reasonable estimates of pre- vs. post-impoundment abundances of various vertebrate indicator species.
Based on the scoping workshop specifications, we developed an initial “straw man” version of the model to act as a basis for critical review and further development in later workshops involving a broader range of scientific expertise and experience with the system. Several subsequent model development workshops ranged in focus from very narrow, with just a few participants working on particular submodel’s relationships and data (sediment transport specialists, basic aquatic production, and fish experts), to a large session (40 people) where we worked on development of all the submodels together.
A final model evaluation workshop was used for critical review and “game playing” aimed at policy screening and identification of key weaknesses and gaps in the model and data. Results presented here are based largely on observations and syntheses by workshop participants from that final session.
It was clear from the scoping discussions that a useful and credible model for policy screening would have to represent the dynamics of a large number of physical and ecological variables, using space and time scales ranging from a few feet and hours (e.g., effects of diurnal flow variation on benthic habitat conditions and juvenile fish behavior) up to the whole-river system over decades (e.g., riparian vegetation development, dynamics of long-lived species, impacts of decadal-scale climate change on hydrology). Yet, to be useful for scenario development and policy gaming aimed at finding imaginative ways to deal with conflicting objectives (Walters 1994), the model would have to be computationally efficient, i.e., capable of running long-term scenarios (40-50 yr) in a few minutes or less of personal computer time. Also, to be of use to managers, we used the English measurement system, and report our results here in those terms.
To meet the conflicting requirements of detail vs. efficiency, our approach was to use different time-stepping and spatial-aggregation assumptions for each submodel. We recognized that we would not be able to reduce the computations and dynamic rules of change to any single, basic temporal and spatial unit that could be repeated to “construct” whole-system dynamics by brute force. Accordingly, our approach to the development of each submodel was to start out by discussing and thinking about the processes involved in that part of the system on fine scales (e.g., sediment movement within a single debris fan-eddy complex, juvenile fish feeding along a rocky, diurnally varying shoreline), and then asking how we could integrate or average these fine-scale dynamics to produce relatively simple analytical relationships for net changes or average conditions over larger scales (e.g., river reaches tens of miles long). In some cases, we relied on existing detailed models, and synthesized results in a set of functions that could be used within GCM.
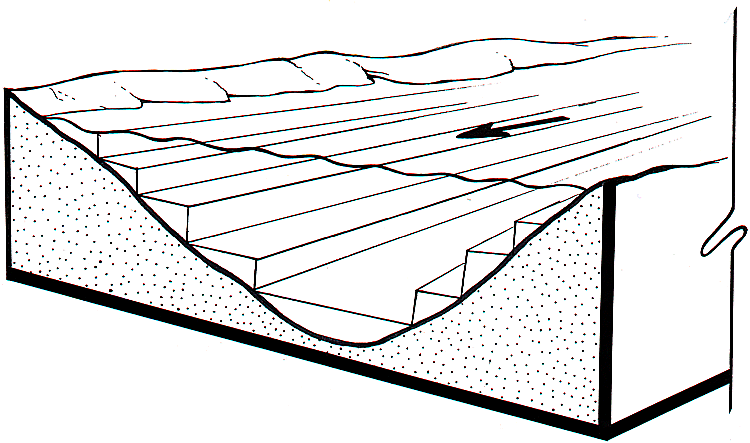
Computational tests, policy concerns, and discussions of space-time patterns with experienced scientists led us to aim for output of model predictions at time steps no coarser than a month, and river reaches no longer than about 30 miles (50 km). That is, we knew that no matter how much computational detail we might avoid by judicious averaging and integration, the model would need to output its basic predictions at scales no larger than months and tens of miles. Further, we knew that we would need to explicitly predict spatial variation in some factors much more finely, in particular, cross-sectional changes in sediment distribution, substrate types, and vegetation from the center of the river channel to elevations high enough above the maximum river stage not to be directly influenced by river dynamics (e.g., desert plant community, cliffs, etc.). To deal with cross-sectional data and dynamic variation, we decided to divide the river within a set of measured cross sections (Randle and Pemberton 1987) into a set of 2-ft (0.6-m) “slices” or contours (Fig. 3).
Besides computational efficiency and lack of detailed space-time data, we had two additional reasons to avoid unnecessary computation of detailed changes at smaller scales than monthly and cross-sectional depth slices within reaches (e.g., by computing changes over a very fine raster map of habitats). First, there has been a tendency in recent ecological modeling exercises to confuse computational complexity (and long model execution times) with realism and precision in model predictions, pretending that a model is somehow “better” if it requires more computing time. In most cases, computational complexity arises not from functional complexity in the relationships considered, but rather from unnecessary repetition of simple calculations (i.e., the apparent “detail” of most models is simply misleading). Second, application of analytical methods to reduce computational complexity can provide insights about fine-scale dynamic variation that could easily be missed in examinations of results from brute-force computations.
We used four analytical techniques to improve computational efficiency and provide insights about effects of fine-scale dynamic variation.
- Variable speed splitting. Variables like algal biomass that turn over rapidly are likely to move to and remain near equilibria that vary over longer time-space scales with influential factors such as turbidity. In this case, a simple strategy is to predict only the monthly equilibrium, and to treat this equilibrium as a predictor of the monthly average of the variable. Technically, this involves writing a dynamic equation rate for the fast variation, and then setting the rate to zero and solving for the resulting variable value as a function of influential variables in the rate equation (e.g., algal biomass as a function of mean monthly turbidity and grazing rate).
- Analytical integration of fast rate equations. In some cases, analysis of fast variation leads to linear or simple nonlinear rate equations. For example, juvenile fish behavior in response to predation risk and food availability is expected to result in a quadratic differential equation (linear density-dependent mortality) for decline in juvenile numbers over time. Integrating such equations over time scales of less than a month allows variation in influential factors (such as food and predator densities for juvenile fish) over scales longer than a month.
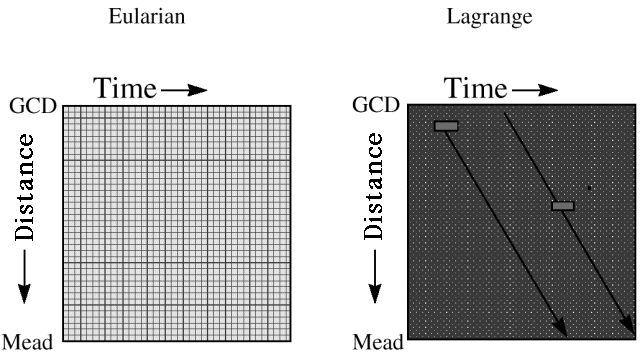
- Sample tracking (Lagrange tracking) of variables with fast space-time movement. One of the nastiest computational problems in river ecosystems is representation of gains and losses of materials and energy suspended in the water column, as water moves rapidly downstream (sediments, detritus, drifting insects, and temperature). We use a Lagrange “sampling” method to deal with such variables (Fig. 4): we think of taking a representative sample parcel of water entering the system each month, and following how concentrations change in that parcel due to gains (from atmosphere, river bottom, and tributaries) and losses (sinking, decomposition, and heat loss) as it moves downstream. Dynamic change along each Lagrange sample track is assumed to follow relatively simple linear dynamics (dx/dt=a - bx, where a is input rate, b is loss rate, and x is reset at each at the time when the sample parcel passes each tributary input point), for which we can obtain an analytical solution for downstream concentration changes.
- Representation of rapid changes under extreme conditions as “event” changes. Some policy options and natural phenomena produce rapid changes in this system. For example, a managed flood event of sufficient magnitude can quickly scour accumulated vegetation from backwater areas, a high sediment input event from tributaries can scour or smother large numbers of benthic invertebrates, and a single low weekend flow (i.e., low releases occur when weekend power demand is low) can desiccate substantial areas of algal cover and associated benthic invertebrates (Angradi and Kulby 1993, Blinn et al. 1995, Stevens et al. 1997b). For plant and invertebrate variables, we check each simulated month for such extreme conditions, and apply mortality factors as point or event proportional losses in abundance. Therefore, we do not try to represent or track all of the transient changes occurring over the short mortality period.
Of course, none of these techniques is guaranteed to produce a satisfactory representation of fine-scale dynamics: the results of each must be judged by careful comparison to data, and to test computations from “mini-models” that make less restrictive assumptions (e.g., a dynamic model for algal biomass development that does not assume biomass remains near equilibrium).
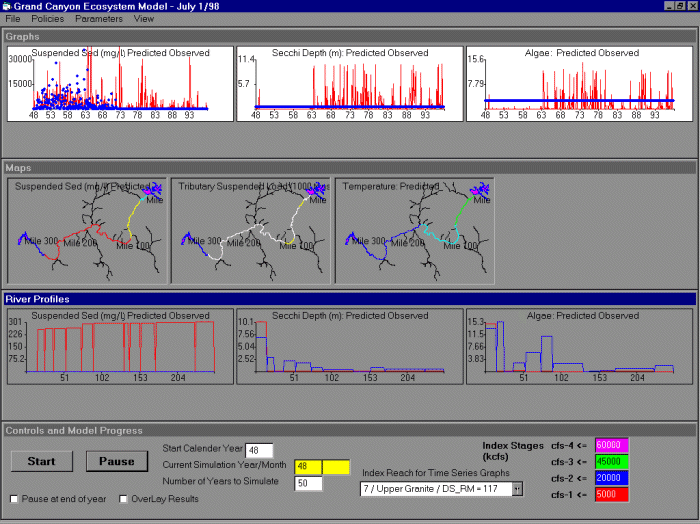
We programmed GCM in Visual Basic 5.0 to provide a flexible and easily modified graphical “shell” for both programmers and users to interact with the model (Fig. 5). This shell presently consists of four parts: (1) data management routines for entering historical “driving” information on water flows and sediment, and reference biological and physical data for comparison with model predictions; (2) graphics display routines for storing and displaying simulation results in various formats (time plots, spatial maps, and downstream and cross-section profiles); (3) a simulation control system (several menus and display windows) for defining scenarios (policy variable choices, biophysical parameter choices) and controlling simulation runs; and (4) a set of submodels for dynamic changes in key parts of the ecosystem.
Basic historical data are stored in easily edited spreadsheets linked to the GCM shell. These data include: (1) monthly historical water flows 1948-1997 from GCD and from major tributaries, i.e., Paria River, Little Colorado River (LCR), and historical within-month statistics summarizing diurnal and weekday-weekend variation in flows; (2) historical suspended sediment concentrations in the mainstem and total inputs from major tributaries; (3) physical reach characteristics including cross-section profiles, stage-discharge relations, statistics on geomorphology (e.g., number of debris fans, return current channels), sand storage potential, and substrate and vegetation composition by depth slice; and (4) scattered samples, mainly since 1991, for upstream-downstream spatial profile information on ecological indicators such as temperature, secchi transparency, benthic algae density, benthic insect density, and counts/relative abundances of some animal species (e.g., birds, fish).
Beyond the main GCM shell, we developed a constellation of spreadsheet “mini-models” to examine particular dynamic relationships and data in more detail. For example, we developed a population dynamics/stock assessment model for rainbow trout, using various fisheries assessment methods with historical catch rate, fishing effort, length frequency, and stocking data, to reconstruct past patterns in juvenile survival and growth. Similar, but simpler, population models for humpback chub and flannelmouth sucker helped us to obtain growth rate and longevity estimates. A mini-model of carp feeding allowed us to evaluate how much the carp population in the Glen Canyon Reach from below GCD to Lees Ferry would have to increase under warmwater release scenarios to severely damage the clear-water primary production system. A fine-scale spatial model at 0.5-mile (0.8-km) river reaches was developed to examine variation in insect drift density among reaches and to test alternative assumptions about average times that individual insects spend drifting.
GCM is a high-resolution linked-reach model, driven at the bottom of the food chain by space-time variation in abiotic parameters such as water flow and turbidity. Aquatic and terrestrial primary production submodels provide direct and indirect (autochthonous and allochthonous detritus) food supplies to simulated aquatic and riparian insect communities. These insect communities (represented in the model only by reach-scale biomass densities) then provide food for insectivorous fishes and birds, which are preyed upon by simulated predator populations such as Peregrine Falcon, brown trout, and channel catfish. In fact, the food chain computations for selected animal species involve diet composition assessments that result in a more web-like structure (juvenile fish feeding on insects, adults on small fish, mixed terrestrial and aquatic insect feeding, etc.), but a key organizing notion in model development was to represent how the vertebrate community is supported by a production system that is variously vulnerable to impact from changes in dam operations. However, GCM is not simply a food chain model: at the top (vertebrate populations) level in the chain, we also explicitly represent possible direct impacts of a variety of habitat factors (temperature, turbidity, availability of warmed tributary and backwater areas for spawning and juvenile rearing). These factors can moderate (or exaggerate) trophic interactions and, in some cases, can directly cause mortality (e.g., thermal shock to juvenile fishes entering the cold mainstem from tributaries). Further, GCM contains an “overview” submodel of economic and recreation values to predict several indicators of economic performance (power revenues) and recreational benefits (rafting, angling).
Development of food chain models in the presence of strong productivity gradients for analysis of policy impacts requires careful consideration of factors that limit trophic interactions, such as “bottom-up” vs. “top-down” (trophic cascade) effects (Oksanen et al. 1981, Sih et al. 1985, McQueen et al. 1986, Power 1990, 1992a,b, Strong 1992, Sih and Wooster 1994, Wooster 1994). Generally positive correlations along productivity gradients between abundances at successive trophic levels are indicative of bottom-up control (predators are unable to limit prey abundance). Such patterns are the rule in Grand Canyon because algal and aquatic invertebrate biomass is positively related to fish and avian biomass and diversity (Stevens et al. 1997a,b, Valdez and Ryel 1997). This is not surprising, considering the complex spatial structure of the lotic ecosystem, with numerous opportunities for donor control of materials such as detritus and drifting/emerging insects, complex prey refuges, and opportunities for behavioral response to predation risk, etc.) In the submodels described next, we allow for the possibility of top-down effects (additive effects on mortality rates at each trophic level of increasing abundance at next trophic level). However, to predict observed abundance gradients, we generally have had to assume that these effects are weak.
Table 1 summarizes basic submodel structure in terms of main state variables considered, spatial and temporal resolution of calculations, and type of dynamic equations used for prediction. The following subsections provide further detail on the rationale and assumptions for each submodel, and basic model results comparing simulated and observed state variable values for those variables with reasonable historical data.
|
Table 1. Main state variables, scales, and computational methods for the GCM ecosystem model for the Grand Canyon.
|
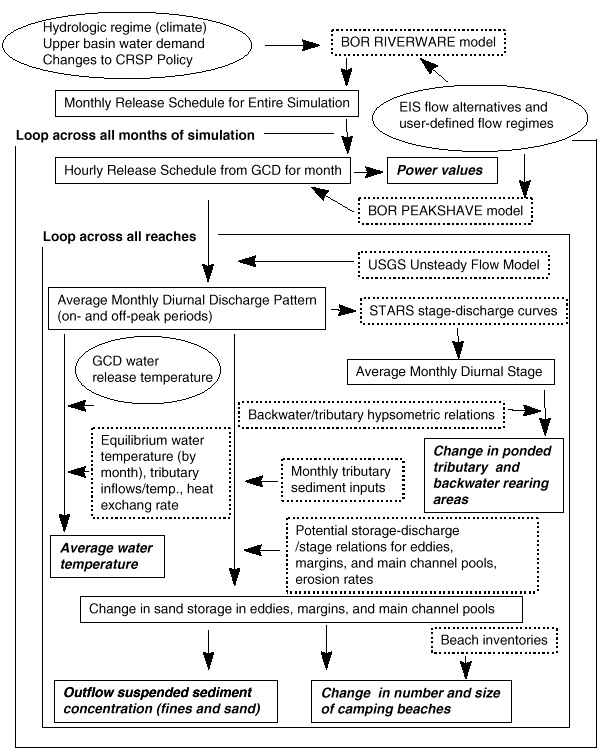
The physical submodel consists of four main components (Fig. 6). An operations component simulates monthly and hourly release patterns based on historical water inflows to Lake Powell, annual and monthly operating rules that are based on the “Law of the River” (as described in Nathonson 1980), user-defined flow constraints (e.g., minimum and maximum flows, ramping rates, maximum daily flow change), and hydroelectric power demand. The “Law of the River,” as applied to the Colorado River, is a collection of rules (Federal and State statutes, interstate compacts, court decisions and decrees, an international treaty with Mexico, and criteria and regulations determined by the Secretary of the Interior) that affect the operation of Glen Canyon Dam. A flow-routing component moves water from reach to reach, accounting for tributary inputs and changes in diurnal wave speed and shape with discharge and distance from the dam. A sediment budget routes sediment delivered from tributaries below GCD to Lake Mead, based on storage potential within eddies, channel margin, and main-channel pool morphologies. A water quality component simulates the downstream change in average monthly water temperatures.
|
Fig. 6. Overview of physical submodels. Text enclosed in oval shapes denotes parameters that can be manipulated by the user to simulate flow and temperature management.
|
Hydrology
For base simulations, GCM uses the historic monthly dam release volumes (or volumes past Lees Ferry prior to impoundment in 1963) to drive predictions. These monthly volumes are the result of the natural hydrology between 1948 and1997, combined with rules that drive annual and monthly water management decisions on the Colorado River to uphold current water policies. The use of historical water releases is ideal for model validation (Does the model reproduce observed changes in physical and biological resources over time?) and policy comparison (What would have happened in the past had the system been managed differently?). However, for more robust policy analysis, historical release data (1) do not provide a representative sequence of future hydrologies (e.g., due to climate change); (2) do not reflect future changes in upper-basin water demand; and (3) do not allow modification of the operating rules governing annual and monthly water releases at GCD (i.e., modifying some components of the “Law of the River”). We therefore linked our model to RIVERWARE, a simulation program used by the Bureau of Reclamation (BOR) to make annual and monthly operating decisions for the Colorado River (see www.usbr.gov/rsmg/warsmp/riverware/index.html), to assess the effect of these long-term/wide-scope policy alternatives on key indicator variables.
We use an existing model developed by BOR and the Environmental Defense Fund (PEAKSHAVE, Harpman and Rosekrans 1996) to predict the hourly release pattern from GCD over each month of the simulation. PEAKSHAVE is a computer program that determines the optimal pattern of water release to maximize power values within a month, given flow constraints, the total monthly release volume, and an hourly aggregate load curve for each month of a typical year. We summarize the hourly discharge release over each month by computing average diurnal pattern (cubic feet per second for each hour over a typical 24-h period) for on-peak (Monday-Saturday) and off-peak (Sunday) demand periods. On-peak and off-peak periods must be modeled separately because of potentially harmful biological effects of weekend low-flow periods.
On- and off-peak diurnal discharge hydrographs from GCD are routed downstream to Lake Mead using a reach-averaged model of diurnal discharge wave propagation developed by the USGS (Wiele and Smith 1996, Wiele and Griffin 1997). The model simulates both the change in wave speed with discharge and how the wave shape is altered as it progresses downstream. These characteristics are critical to the physical and biological environments because they affect the duration and extent of maximum and minimum stage in each reach, as well as the time of day that the maximum and minimum flows occur (Appendix 1). Stage in each modeled reach, predicted as a function of discharge and stage-discharge rating curves derived from the STARS model (Orvis and Randle 1987, Randle and Pemberton 1987), is used to determine how long each depth slice (
A sediment budget for the Colorado River ecosystem is required to assess the effects of diurnal flow alternatives and beach/habitat building flows (controlled floods) on: (1) creation and maintenance of camping beaches and habitat for riparian vegetation and fish; (2) mainstem suspended sediment concentrations affecting aquatic productivity (through light attenuation and scouring); and
(3) maintenance of cultural resources such as archeological sites. Although the model awaits refinement in sediment storage functions, it simulates decadal-scale patterns in sand storage in different types of depositional environments (eddies, channel margins, main-channel pools) and reproduces trends in historical mean monthly suspended sediment concentrations. These provide rough predictions of changes in camping beaches and water clarity/scouring that affect aquatic
productivity for broad-scale policy analysis. The coarse resolution of our sediment submodel is inadequate to address fine-scale sediment management questions (e.g., the duration of experimental floods, effects on archeological sites), but these issues are being addressed by current research and modeling efforts (S. Wiele, USGS, Lakewood, Colorado, USA, unpublished data). Measurement error in sediment transport data used to tune the model is too high to resolve whether the long-term trend in channel sand storage is stable or slowly degrading (Topping et al. 2000a). The sediment budget in GCM and current understanding do not allow the translation of changes in sediment storage to changes in fish habitat (i.e., creation and maintenance of backwaters). Even if backwater changes could be predicted, they would be of limited value, as their influence on native fish recruitment has yet to be demonstrated.
In the GCM sediment budget, sand is tracked reach-by-reach within eddy, main-channel pool, and channel margin morphological environments. Tributary inputs of sediment from the Paria and Little Colorado River (LCR), sediment discharged from GCD, and the average diurnal on-peak hydrograph for each reach over the month are the forcing variables that drive the sediment model predictions. Historical monthly tributary inputs of fine particles (silt and clay <0.0625 mm) and sand (0.0625-2.0 mm) are based on the USGS-Paria model (Topping 1997) or sediment rating curves (D. Topping, USGS, Denver, Colorado, USA, unpublished data). The maximum potential of eddies (J. Hazel, M. Kaplinski, and R. Parnell, Northern Arizona University, unpublished data), main-channel pools (T. Randle, BOR, Lakewood, Colorado, USA, unpublished data), and channel margin environments to store sand is predicted through a series of reach-specific potential sand storage-water discharge relationships (Appendix 2). Differences between potential storage, current storage, and the sediment inflow in each modeled month are used to determine how much sand flux occurs in each environment. The sum of eroded sand and inflow to the reach that is not deposited predicts outflow sand concentrations and forms the upstream boundary input for the next reach downstream.
Main-channel pools are treated as a single unit for each reach, whereas eddies and channel margins are divided into a series of horizontal slices (Fig. 3) to track the fraction of each environment that is submerged and subjected to different erosive forces. Empirically derived above-water (eolian) and submerged (tractive) erosion rates (J. Hazel and M. Kaplinski, Northern Arizona University, unpublished data) alter sand storage in each environment. Erosion rates are dynamically adjusted during the simulation based on the volume available for storage, ranging from full (no storage capacity) to empty. This roughly mimics the effects of grain size evolution (coarsening of particles on the bed) that decreases downstream sediment transport rates over the course of a high-flow event (Rubin et al. 1998, Topping et al. 2000b).
The sediment submodel reproduces some long-term dynamics in sand storage documented in the system (Appendix 3). Prior to impoundment, storage in eddies and main-channel pools showed high interannual and seasonal variability. Higher elevation regions of eddies inundated at the 45-60 kcfs (thousands of cubic feet per second; 1274-1699 m3/s) stages are regularly replenished by large spring floods. However, these same floods deplete main-channel storage pools and lower-elevation eddy environments, which are exposed during summer low flows, increasing storage potential when tributary sediment delivery is high. Following impoundment and elimination of natural spring floods, these upper-eddy deposits are no longer inundated and begin to erode. Interannual variability in storage in eddy and main-channel pool environments is reduced because of the elimination of the spring flood and the loss of low summer flows, which allow storage of sediment in the main-channel and lower-eddy deposits. Sand stored in the 20-45 kcfs (566-1274 m3/s) range is maintained by regular high releases up to 31.5 kcfs (892 m3/s) from GCD to meet power demands during high-use periods. The effects of the unplanned 1983-1986 floods include temporary flushing of lower-eddy deposits and main-channel pool environments, and the replenishment of sand at higher elevations (45-60 kcfs). Reduced daily flow fluctuations associated with interim flows after 1990 result in a decline in sand storage in the 20-45 kcfs range, which is no longer inundated until the occurrence of higher monthly releases (mid-1990s) and the implementation of the MLFF alternative (daily flows limited to 25 kcfs) in 1996.
The availability of camping beaches is an important component of the highly popular whitewater rafting experience in the Grand Canyon (Kearsley et al. 1994). The sediment model allows us to provide coarse statistics of temporal change in the numbers and size of camping beaches. Beach availability is compared to the camping demand estimated by the recreation-rafting submodel to identify bottlenecks within reaches and over time, and how they vary under different flow regimes (diurnal changes and spike flows). Changes in beach availability are based on the simulated amount of sand above the maximum discharge level inundated under normal operations (the discharge level at which camping beaches are not typically inundated), existing beach habitat inventories (e.g., Kearsley and Warren 1992, Kearsely et al. 1994), and empirical relationships between camping beach availability and reach-wide sand storage estimates in eddy environments
(J. Hazel and M. Kaplinski, Northern Arizona University, unpublished data).
Average monthly water temperatures for each reach are computed using the Lagrange tracking method described in Appendix 4. The relationship computes gains and losses of heat as water moves down the river. Predicted temperatures at the downstream boundary of each reach are driven by the release temperature from GCD, equilibrium water temperature, temperature and volumes of tributary inflows, and a heat exchange coefficient. Historical average GCD outflow temperatures for each month (B. Vernieu and J. Korn, Grand Canyon Monitoring and Research Center, Flagstaff, Arizona, unpublished data) are used for the release temperatures, and the user can modify these values to simulate the effects of a selective withdrawal structure allowing warmer releases from GCD. The upstream boundary
temperature for each reach (Ci in Eq. A4.1) is a flow-weighted average of the predicted temperature from the upstream reach and any tributary inflows. The equilibrium temperature for each month (Ceq in Eq. A4.1) is the temperature that the water would eventually reach if it did not flow; it is a complex function of air temperature, direct insolation, wind patterns, and evaporation. We simply describe the seasonal variation as a table of 12 monthly values. The heat exchange coefficient (v in Eq. A4.1) is again a complex function of environmental conditions and has been parameterized by tuning the model to a wealth of observed spatial and temporal gradients in water temperature (Appendix 5).
Benthic algal communities (mainly Cladophora and Oscillatoria) and the ephiphytic diatioms that they support are apparently the main source of food for aquatic insects. Insect biomass declines dramatically downstream from the area of high primary production below Glen Canyon Dam (Stevens et al. 1997a), indicating that other detritus sources are insufficient to support high insect production (i.e., the system does not change from autochthonously driven to allochthonously driven, maintaining high total food supplies for aquatic insects all along the river). That is, the whole downstream aquatic ecosystem appears to be driven by changes in aquatic primary productivity, particularly in the upper reaches.
Two main factors appear to influence algal biomass and production: (1) turbidity, which varies dramatically on seasonal and interannual time scales downstream from the Paria and Little Colorado Rivers; and (2) diurnal flow variation, which subjects algal communities in shallow waters to complex patterns of variation in light penetration and potential mortality due to desiccation. Further complicating the impact of diurnal flow variation is that diurnal stage (depth) waves at Glen Canyon Dam move down through the system much faster than do water parcels, taking about two days to move from GCD to Lake Mead (Graf 1995, Wiele and Smith 1996). Communities near the dam are subject to deeper water during the day (which tends to reduce production due to reduced light penetration), and then nocturnal drying. The net effect is that there is little algal development in the diurnal “varial zone” and in depth slices just below this zone (Appendix 1). However, communities about 12 h wave travel time downstream are subject to the opposite pattern: minimum stages at midday permit some primary production even when turbidity is high, and increased stage at night protects such depth slices from desiccation so that there can be relatively high primary production at the lower margin of the varial zone.
To simulate these complex relationships, we followed the structure developed by Yard et al. (1993) to model aquatic productivity based on inorganic sediment interference with benthic photosynthetically active radiation. The model computes hourly calculations of potential primary production rate (a function of depth and turbidity) and desiccation time for each depth slice in each reach, for a typical 24-h period of diurnal stage fluctuation each simulated month. Equilibrium biomass for the slice is then predicted from these typical production and desiccation rates. For further details, see Appendix 6.
Simulated and observed depth and downstream distributions of algal
biomass accord quite well with observations (Appendix 7). GCM predicts substantial
interannual and even decadal-scale variation in algal biomass
development in lower river reaches (particularly below the Little
Colorado River), due to interannual variation in sediment delivery
from tributaries (Appendix 8). Studies in 1994-1996 revealed considerable algal (and benthic insect) biomass development in the lower reaches, whereas studies in 1991-1993 and in 1997-1998 showed low biomass there. This dynamic may lead to a misunderstanding and debate about productivity in the lower reaches, and emphasizes the need for long-term monitoring programs in the system.
Aquatic insects form the primary food supply for most fishes and some riparian bird species (e.g., ducks, swallows). During model development, there was considerable debate about whether the natural system had a productive insect community (and, hence, about whether it could have supported substantial bird and fish communities). Stevens et al. (1997a) reported little anecdotal evidence of pre-dam waterfowl from early river runners and other observers of the natural system. At present, there is a dramatic downstream decline in insect densities below the clear-water Glen Canyon Reach, suggesting no significant allochthonous replacement of detritus food supplies from terrestrial sources within the Canyon. Yet, observations in the Cataract Canyon area upstream from Grand Canyon (Haden et al. 1997) indicate a higher aquatic invertebrate diversity, but not biomass (Stevens et al. 1997b), apparently supported by detritus sources in the Colorado River headwaters.
Our modeling approach was to divide insect biomass into three main biomass categories: grazers (mainly Gammarus and chironomids), detritivores (mainly Simulium), and combined drift. We calculate mean monthly biomass densities of grazers and detritivores for each river reach (for details, see Appendix 9), and then use the Lagrange sampling method (
Generally, we can reproduce measured spatial patterns (averaged over time) in the biomass density and composition of grazers and detritivores quite well (Appendices 7 and 8), but seasonal monitoring data are too noisy to determine whether the model correctly represents finer scale temporal patterns. As for algal production, a key prediction from the analysis is high interannual and even decadal-scale variation in biomass, driven by changes in aquatic primary production and losses due to scouring and burial associated with large inputs of sediment from tributary flooding. In the Glen Canyon Reach just below Glen Canyon Dam, simulated biomass changes from the late 1970s to the present (Appendix 8) show a long-term pattern of interannual change that is also reflected in body condition and juvenile survival estimates for rainbow trout: (decline during the 1980s high flows, low survival during the 1987-1989 highly fluctuating flows, and enhanced survival and recruitment after 1991).
A worrisome problem with this submodel is that it does not predict measured qualitative spatial patterns in insect drift density. Data collected during the 1994-1995 period (Shannon et al. 1996) indicate increasing drift densities downstream through the system, with species composition changes reflecting changes in local benthic communities (i.e., individual insects are not drifting > 6-12 miles, or 10-20 km). To explain this increase, given measured downstream decreases in biomass of benthic insects available to enter the drift, we have to assume (1) that drift rates increase dramatically (10 x) in lower reaches, (2) that there is a large unmeasured biomass component of benthic invertebrates in the lower reaches, or (3) that the measurements were inflated, possibly through extrapolation. Drift densities have been measured for tributaries that could be more productive than the turbid mainstem (Shannon et al. 1996), but these inputs are not large enough to account for the downstream increases seen in the mainstem.
Our aim in this submodel is to represent broad changes in shoreline
vegetation types resulting from changes in flow regimes, and changes
in contributions of detritus and insects from shoreline communities to
the aquatic ecosystem. We simulate biomass dynamics for five main
vegetation types at each depth slice within the reaches. There are
dynamic equations for annual growth-competition relationships (Appendix 10), and for monthly mortality due to
flooding and drying. Each vegetation type is assumed to be capable of
growing on a subset of particle sizes and range of elevations above
current high water (representing water table depth). Monthly flooding
and desiccation impacts are represented by a function relating
mortality rate to duration x depth of flooding (and duration of
desiccation); such curves can be “sketched” by model users
using a mouse-driven entry interface (Appendix 11), along with information about the substrate types upon which each vegetation type can grow.
Lacking detailed data on growth-competition parameters, we “tuned” these parameters to provide roughly the time scales documented for vegetation development following elimination of natural flooding and following the vegetation removal effects of floods during 1983-1984 (Anderson and Ruffner 1988, Stevens and Waring 1988, Stevens et al. 1995; Appendix 12). Because of assumptions about large differences among vegetation types in water table requirements, the competition parameters have relatively little impact in baseline simulations; it is a matter of debate about whether slow competitive dynamics might eventually allow one or another community type to dominate wider elevation bands along the shore.
We assume detritus and terrestrial insect production from riparian communities to be proportional to relative biomass and area occupied by each vegetation type, with large differences among vegetation types (Appendix 11). Generally, faster growing vegetation is assumed to produce more detritus and insects. Lacking direct data on insect population dynamics and production, we assume that insect populations remain close to equilibrium with (i.e., they track changes in) vegetation biomass. Production rates of terrestrial insect drift into the aquatic system are set in order to fit measured drift concentrations for 1994-1995, roughly 10% of drift contribution from aquatic insects (Shannon et al. 1996).
Main differences in dynamics by vegetation community type are assumed to be the following:
We tried to develop rough estimates of detritus production from riparian vegetation as contribution to allochthonous production in the aquatic community. Although estimates of detritus production per unit area from riparian vegetation do not appear large enough to sustain substantial aquatic insect production, there was considerable debate about two issues. First, allochthonous inputs may enter the river from a much wider “catchment” than just the riparian zone (e.g., side-canyon basins), making it impossible to predict total inputs
from any simple areal assessment of riparian vegetation. Second, there are local “hotspots” (mainly eddies and backwaters) of detritus delivery and potential insect production, at spatial scales smaller than we simulate. Such sites could store pulses of low-quality (leaves, large woody debris) detritus from tributary flood events long enough for that detritus to be made available to the aquatic insect community through bacterial and decomposition processes.
We attempted to develop a fairly flexible population dynamics model for representing
reach-scale interannual variation among the 15 vertebrate indicator
species that account for most of the predatory biomass in the
ecosystem (baseline 15 species). The model can be applied to both bird
and fish species, but in the description that follows, we mainly use
terminology associated with fish populations. The population dynamics
model has two main parts (see Appendix 13):
(1) an age structure and (optional) biomass accounting system for
abundance of animals at least 1 yr old, in which we can “turn
off” some time delay effects (e.g., age at maturity) and biomass
accounting to provide simple numbers accounting only (N next
year = survivors plus new recruits) for species with simple life
histories and/or limited life history data; and (2) a complex
recruitment model relating 1-yr-old recruits to parental egg/hatchling
production, food supply, predation risk, and physical habitat
variables such as temperature and tributary rearing area. The concept
in this derivation is that most important population dynamics events
and limiting factors operate mainly on juveniles during their first
year of life, before they recruit (i.e., become large enough to use a
wide variety of physical habitat conditions and to avoid high
predation risks). Species included in the baseline model runs, along
with some basic population dynamics parameter estimates (growth and
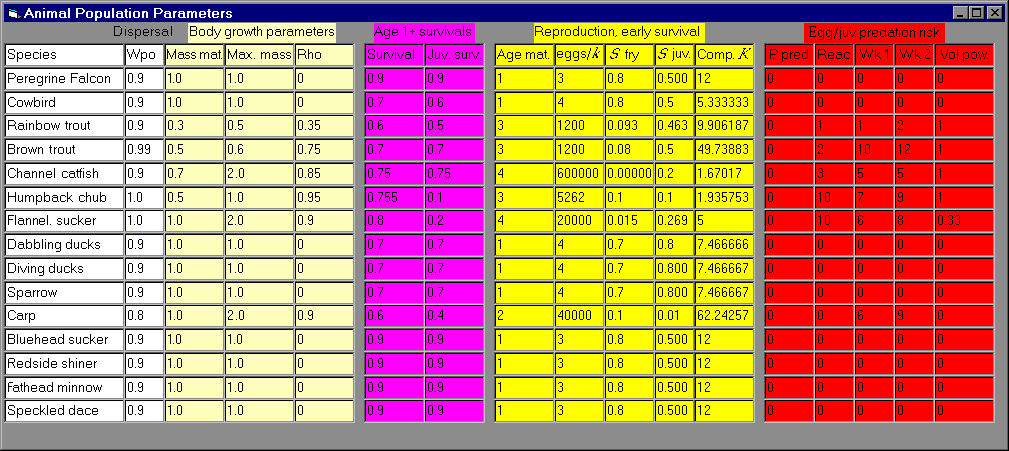
survival rates) are listed in Appendix 14, which shows the model interface for entering and editing this information.
The key component of this submodel is the recruitment relationship, which we derived (Walters and Korman 1999) by considering how evolution has shaped the behaviors of small juvenile fish to deal with three main problems: (1) finding secure resting habitats safe from predation, (2) finding sufficient food to grow enough to eventually mature, and (3) incurring high predation risk while feeding (due to small body size, lack of experience with predators, etc.). Following
arguments in Walters and Juanes (1993), we assume that juvenile animals prefer safe refuge sites (shallow shorelines, under protective rocks and vegetation, etc.) and, hence, are restricted to foraging in relatively small spatial “foraging arenas” near these refuge sites. Spatial restriction of foraging in turn implies that there can be locally intense exploitation competition for food: overall food supplies in the environment may be substantial, but food densities may be reduced substantially in the foraging arenas when juvenile densities in these arenas are high. We assume that juveniles adjust their time spent foraging (and dispersing to find less crowded sites) so as to maintain some basic “target” growth rates (“optimized” through natural selection). Analyses of food production and exchange rates for foraging arenas then imply that time spent in foraging arenas, and hence time at risk to predation in such arenas, should increase linearly with local juvenile density. Thus, if predation risk is proportional to time spent foraging, then juvenile mortality rates should increase linearly with juvenile density. Linear density dependence in instantaneous juvenile mortality rates is the basis of the classic, widely used Beverton-Holt (1957) relationship, which for fishes, predicts the widely observed phenomenon that eventual recruitment is largely independent of egg deposition (i.e., it is limited by factors other than egg deposition) over wide ranges of parental abundance.
The recruitment relationship derived from these arguments has explicit terms for resting (refuge) area and foraging arena physical size (essentially, refined measures of effective habitat size); predation risk per time foraging, which may, in turn, depend on habitat variables such as temperature and turbidity (or vegetation biomass in the case of birds); and apparent food density, which may also depend on habitat factors such as turbidity. In the simulation, we generate time-varying food supplies (mainly aquatic and terrestrial invertebrates for the indicator vertebrate populations considered thus far), and indices of predation risk based on changes in relative abundance of potential vertebrate predators (abundances of other species are included in the list of index species). A convenient feature of the derivation is that predation risk and food effects appear only as a ratio P/F (predator abundance/food density), so we can combine habitat effects on recruitment into two habitat effect types: (1) effects on the risk ratio via effects on predator avoidance and feeding efficiency, and (2) effects on potential food competition through total volumes of accessible foraging arenas.
Because we lack microscale foraging behavior data on juvenile fishes, we have been unable to address one potentially serious weakness in the recruitment formulation. Our derivation is based on the assumption that the behavior of each species of juvenile fish results in a unique foraging arena for that species, within which there can be strong intraspecific competition for food. Effects
of interspecific competition are included in the calculations only through large-scale effects of multispecies exploitation on reach-scale densities of invertebrate food types. We assume that there has been strong selection for microscale behavioral differences among species (diurnal times of feeding, specialization in prey species choice, etc.) to avoid intense exploitation
competition within small foraging areas. However, there may be important interspecific
competition among juvenile fish species in some microhabitats, particularly between native and exotic species in warm backwater and shoreline sites. Thus, the model may underestimate impacts of exotic fishes in the ecosystem, although we already assess these effects to be potentially very large through predation on juvenile native fishes alone.
We simulate a time-varying (reach, month scale) set of physical habitat capacity/risk/food
availability indices including: temperature, turbidity, area of warm tributary/backwater
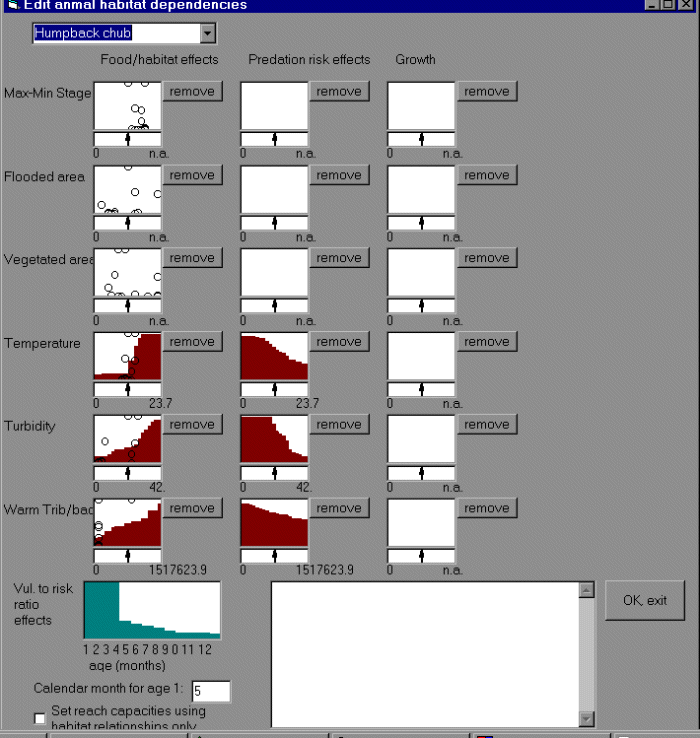
habitat, diurnal stage change (which reduces availability of shoreline refuge habitats for small fish), and total wetted area. A graphical user interface (Appendix 15) allows the user to “sketch” hypothesized relationships between habitat factors and components of the recruitment relationship (habitat size available to juveniles, risk ratio), and adult growth rates.
Lacking reliable total abundance estimates for most vertebrate species, particularly exotic fishes such as carp and channel catfish, we internally scale population carrying capacity parameters in the model so that predictions reproduce spatial trends in relative abundance indices derived from field data. Taking 1993 as a base index year, we calculate recruitment scaling parameters to predict constant abundance over time (equilibrium abundance) if predation risk, food density, and physical habitat factors remain at 1993 levels; available trend data suggest that most vertebrate populations were, in fact, not changing rapidly around that time. For each juvenile vertebrate species, we specify 1993 baseline estimates of the proportion of juvenile mortality due to each modeled predator type, and the proportion of different food types (benthic insects, algae, terrestrial insects) in the juvenile diet. Then the risk ratio (predators/food) calculations are scaled to provide user-specified maximum juvenile survival rates in the absence of competition when predator and food relative abundances are at 1993 levels, and to give proportional increases/decreases with proportional changes in relative abundances away from the 1993 baseline levels.
A really discouraging factor in the development of the population dynamics submodel was that expert workshop participants were unable to reach clear consensus about even the basic temporal population trends for a number of native fish species, particularly endangered humpback chub (Gila cypha) and flannelmouth (Catostomus latipinnis) and bluehead (C. discobolus) suckers. There had been a general supposition among Grand Canyon fish researchers, largely unsupported by objective data, that all native fish species declined in abundance in response to the cold-water conditions created by Glen Canyon Dam (Valdez and Ryel 1997); certainly a few species have disappeared entirely (e.g., Colorado River pike minnow Ptychocheilus lucius, and bonytail chub Gila elegans), although it is not clear whether these extirpations were the result of cold-water releases from GCD or were already well underway at the time of dam construction because of other prior disturbances (i.e., Hoover Dam completion in 1935, and invasions by exotic fishes, particularly carp and channel catfish). Recent data on one major species of concern, humpback chub, suggest that the tributary spawning population in the Little Colorado River may be (and may always have been) specifically adapted to use mainly the tributary habitat (Valdez and Ryel 1997. This population may have increased since 1963 because of favorable growth conditions for older juveniles and adults in the mainstem Colorado River, along with reductions in abundance of some warmwater predators and competitors. Likewise, flannelmouth and bluehead suckers now use mainly warm tributaries for spawning; their juveniles are widely distributed downstream and appear to be successfully rearing in relatively warm and productive backwater habitats. Violent seasonal flooding, followed by very low winter flows, probably prevented development of productive and accessible backwaters in the natural system, and winter periods of low and relatively stable flow were probably too short and cold to permit much development of mainstem benthic food sources for these species.
After much discussion in the model development workshops, we were unable to decide on the direction of change for the indicator fish species in the ecosystem. We can choose habitat linkage functions in the simulation model for three key native species (humpback chub, flannelmouth, and bluehead suckers) that result in higher or lower populations for pre-dam simulations. Trophic changes alone result in predictions of reduced populations in the pre-impoundment simulations
(based on reduced invertebrate food supplies and increased competition and predation from warmwater exotic species), but we were easily able to manipulate the habitat linkage functions, particularly for temperature and turbidity effects on risk ratios and habitat areas, to provide reasonable and credible functional forms that resulted in the opposite prediction. Dam operations may strongly affect endangered fish populations, but historical fish population data do not allow us to evaluate this hypothesis.
Many socioeconomic indicators are affected by the operation of Glen Canyon Dam. In this analysis, we consider the direct economic costs of alternate flow regimes on power revenue generation. We also model the effects of flow changes on whitewater rafting in Grand Canyon and flow/temperature effects on trout angling in the Glen Canyon Reach immediately below the dam. Our rafting index is a comparison of campsite demand and availability, whereas our angling indices track changes in total catch, catch rates, and effort. Regional economic impacts and economic values of rafting and angling in each month of the simulation are computed based on previously published models (Bishop et al. 1987, 1989, Boyle et al. 1993). Regional economic impacts are based on estimates of the impact of commercial and private trips for individual rafters or anglers (adjusted to 1997 dollars) expanded by the number of trips simulated in the model. Regional economic impact per trip is assumed to be static over time, whereas the economic value varies according the mean monthly discharge and the extent of daily flow fluctuations.
Power values: The economic value of electricity varies substantially over time, depending on the demand for power. Demand and, consequently, river flows, are higher during the summer and winter when required for cooling and heating, and are higher during the day when businesses are open, and lower at night and on weekends. These patterns are fundamentally different from those of the pre-dam hydrograph. Changes in daily and monthly operation of GCD associated with different release alternatives will have no effect on the annual power generation (i.e., the same amount of water will be passed through the turbines over the course of a year), but will affect the schedule of electrical output and, hence, its value (National Resource Council 1996).
The PEAKSHAVE model (Harpman and Rosekrans 1996) is used in our simulation to predict the hourly release pattern from GCD and power values generated for each month, given a set of operating constraints (minimum and maximum daily flow, maximum daily upramp and downramp rates, maximum daily flow change) and a total monthly release volume. Estimates of the monthly value of power are based on 1996 spot market price data that represent current conditions in the
regional power market (Harpman 1999a). The economic value of power estimated over a long-term simulation assumes no change in base generation of resources affecting demand and price (i.e., a short-run economic analysis).
The costs of various mitigative flow constraints (e.g., MLFFA, the modified low-fluctuating flow alternative) are computed by comparing monthly economic values of power with those generated under the No Action alternative, the historic operating regime allowed when plant operations were not restricted by ramping rates and other constraints intended to benefit downstream ecology. In a representative water year (11.3 x 106 acre-feet released from GCD) under the No Action alternative, the model estimates that Glen Canyon Dam will produce approximately U.S.$70 million worth of energy (in 1996 dollars). By comparison, under the current MLFFA policy, GCD will produce $64 million, equivalent to an annual loss of $6 million or 8.6% (Harpman 1998). Note that in an economic analysis contributing to the 1995 GCD Environmental Impact Statement (BOR 1995), respondents in the market area indicated a willingness to pay well in excess of the proposed foregone power revenues to improve the Colorado River ecosystem in Grand Canyon (Welsh et al. 1999).
Whitewater boating economics: Sediment deposits along the Colorado River in the Grand Canyon serve as campsites for rafting trips. Since completion of GCD in 1963, there has been a noticeable loss of suitable campsites, principally due to erosion, lack of sandbar replacement with incoming sediments, and vegetative succession. The gradual loss of campsite space along the river corridor is a concern because of intense rafting use. Over 22,000 river runners use the system each year (Kearsley et al. 1994), resulting in an annual regional economic impact in excess of U.S.$20 million (Bishop et al. 1989).
The rafting component of our model compares the demand and availability for campsites on a reach-by-reach basis for each month of the simulation. Sediment budget predictions of reach-wide changes in sand storage for eddy environments are used to calculate the change in the number of beaches and in the frequency of small, medium, and large beach size classes. Campsite demand for each beach size class is controlled by a number of parameters that the user can manipulate including: (1) maximum number of trips per year for each of four group types (commercial-oar, commercial-motor, private-oar, and research-motor); (2) maximum number of launches per day; (3) average number of persons and length of a typical trip for each group; and (4) relative preference for rafting in different months of the year. We initialize the model using the full set of inventoried beaches (Kearsley et al. 1994) and then populate them with groups based on the parameters, as well as a preference factor that reflects the “desirability” of each beach, accounting for such factors as camping quality, access, and location relative to sights of interest. The total number of small, medium, and large beaches required in each reach is computed and compared with the reach-wide estimate of beach availability predicted by the sediment model.
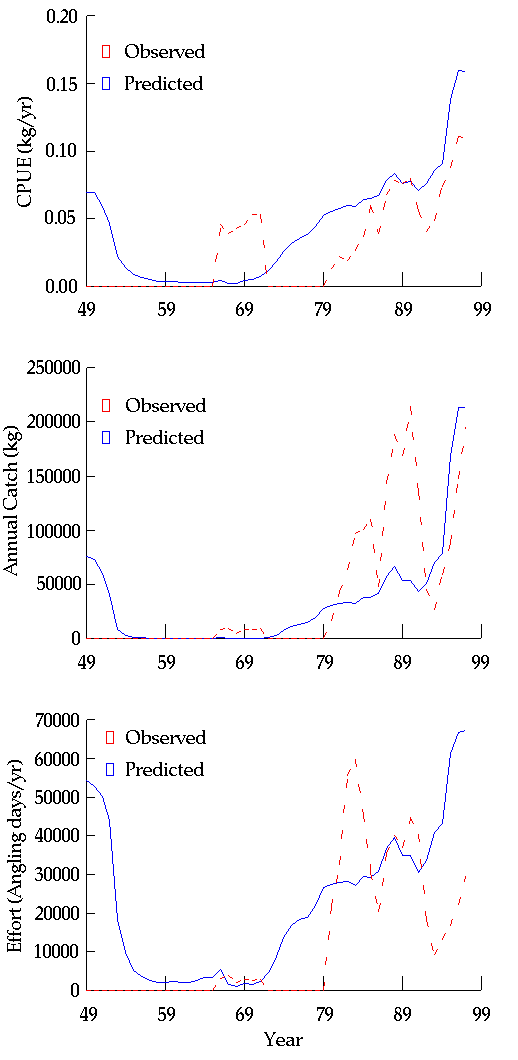
Trout-angling economics: The Glen Canyon rainbow trout fishery, located in the first 16 miles downstream of GCD, is one of only two blue-ribbon stream fisheries in Arizona and is used by over 19,000 anglers each year (NRC 1996), resulting in a regional economic impact in excess of U.S.$3 million (Bishop et al. 1989). Many flow/temperature discharge regimes being considered for beach/habitat building and recovery of native fish species are believed to be potentially harmful to this fishery. Large daily fluctuations associated with maximum economic power values also maximize the loss of the aquatic food base due to algal/aquatic insect desiccation and redd dewatering. Higher temperature releases, which could be achieved through the construction of a selective withdrawal structure, have the potential to greatly increase planktonic food resources for young trout, but also may increase population sizes of competitors and predators. Although whirling disease (Myxobolus cerebralis) has currently not been detected in trout in the Grand Canyon, it may already be present, but kept in check by low water temperatures. Increasing water temperatures may increase the risk of a whirling disease outbreak.
The Glen Canyon reach trout population is simulated using the same framework applied to other species in GCM, but additionally, we explicitly model stocking rates and angling mortality. The trout-angling submodel predicts changes in total catch, catch rate, and effort over time. Angling mortality is computed by specifying a monthly set of catchability and effort rates that reflect historic catch statistics. Catchability is assumed to increase with fish size. Effort can be held constant over a simulation or can vary dynamically based on catch per unit effort. When effort is allowed to vary dynamically, the model is able to reproduce the broad changes in relative trout abundance and utilization that have occurred since construction of GCD (Appendix 16). However, there are some obvious errors in the predicted timing of events due to dynamic effects (that GCM does not simulate), such as time-varying stocking rates, and changes in angler preferences, behavior, and management (anglers now release most fish, whereas until the late 1980s, they exerted extreme exploitation pressure).
Cultural resource indicators: We have not modeled the effects of dam operation on cultural resources in Grand Canyon. Perhaps the most important issue here is the erosion of archeological sites by arroyo cutting in short, ephemeral streams that drain the terraces of the river corridor (Hereford et al. 1993). The reduction of sediment load and elimination of the annual flood in the post-dam era may have reduced the elevation of depositional environments and are hypothesized to intensify arroyo cutting and accelerate the exposure of archeological sites. A second issue concerns the potentially intensified erosion of banks (due to reduced sediment load from dam operations) that support very high-elevation terraces (inundated at discharges in excess of 300 kcfs) where archeological sites are located. A third issue concerns changes in the abundance and distribution of native and non-native ethnobotanically important plant species caused by dam operations. The first two issues require high-resolution predictions based on multidimensional hydrodynamic models that are too data-intensive to be used in our long-term, whole-system assessment model. Changes in ethnobotanical resources may be coarsely simulated in future efforts by associating each plant species with one of the five riparian community types that we model, and then computing an ethnobotanical-weighted biomass index based on the relative abundance of each community type.
Preliminary screening of broad policy alternatives with GCM has involved qualitative assessment of general response directions and time scales for a wide set of performance indicators (Table 2). To obtain these assessments, we primarily used “history reference” simulations: we run the model with historical hydrological forcing inputs, but with altered management of these inputs at various time periods. Comparison of state variable changes between scenarios involves questions of the form “What would have happened had the system been managed differently?”, rather than “What will happen in future if it is managed differently?”. We feel that this approach provides a more credible way of comparing policy alternatives than making general predictions about a future filled with unknowable hydrologic patterns.
a Seasonally adjusted steady flows remove diurnal variation, have spring-summer peaking, and relatively low winter flow in order to move toward a more natural seasonal hydropattern.
b Assumes the capability to release warm Lake Powell surface waters for 2-3 months/year.
Several broad results have been apparent in this screening:
Point (5) is particularly important in terms of the basic AEAM modeling objective of narrowing the range of policy options for future analysis and experimental evaluation. Unless really innovative options and restoration methods are found, it appears that future policy exploration might best be concentrated on “tinkering,” with relatively minor adjustments in diurnal flow variation and artificial floods (planned beach habitat building flows - BHBFs), along with use of quite different management tools, such as direct control measures for undesirable exotic species such as carp and brown trout.
In hindsight, most of the major policy predictions of GCM could have been obtained with much simpler models and analyses of historical response data, and some responses have been predicted in the literature on this ecosystem. This is typical of detailed models for environmental management, but without “overbuilding” the model initially, we would have been left with nagging doubts about whether some small-scale aspect of the dynamics might produce large “emergent” effects (Walters 1986).
Among the most valuable insights of the GCM is the identification of information gaps and uncertainties in response direction. The following subsections review some findings from GCM policy screening that are particularly important in terms of future planning for Colorado River management. These findings are related to the qualitative (response direction) uncertainties in Table 2, particularly sustainability of options for sand management, and efficacy of options for enhancing or restoring “natural” ecosystem values, such as native fish populations. In the absence of the desire to restore “natural” ecosystem values, future management debates are likely to focus on issues related to foregone power revenues, maintenance of beaches for recreation, and maintenance of the Glen Canyon trout fishery.
The beach/habitat-building flow experiment of 1996 indicated that at least some beaches can be temporarily restored to more usable/productive states by controlled flooding (Hazel et al. 1999, Schmidt et al. 1999a). Although additional small backwaters were created during the 1996 flood, most of these quickly degraded in size, and backwater area is declining overall (L. E. Stevens, unpublished data). Sand movement into upper-eddy deposits was mainly from in-system storage (channels, lower portions of eddies) deposited from previous tributary floods, and substantial quantities of sand are exported during each flood event. The extent of sand storage potential in critical sediment reaches (Marble Canyon, between the Paria River and the LCR) in the lower portions of eddies and the main channel is still uncertain. If storage capacity is small, artificial floods will need to occur shortly after tributary floods (usually in the late summer),
especially to conserve silt and clay sediment components. If storage capacity is large, artificial floods could be delayed for months or years after major inputs from tributaries, until the winter-spring period, when current institutional agreements allow them to occur. Unlike the biological risks associated with some management alternatives (e.g., higher temperatures enhancing nonnative predators/competitors of native fish), potential depletion of mainstem sediment reserves due to controlled floods appears unlikely to have long-lasting effects
based on the most current research. It has been estimated that 10-20% of sand and 100% of silt and clay material input during tributary floods (except a minor fraction deposited in backwaters) is exported within approximately 2 wk, with the remaining sand exported over 1-2 yr (D. Topping, USGS, Reston, Virginia, personal communication). This analysis suggests that the mainstem supply of sand must be rejuvenated relatively often by tributary floods or there would be little sand left in the main channel and eddies, given such short retention times. In contrast to this perspective, the 1996 BHBF (beach/habitat-building flow) rejuvenated sandbars system-wide (including the sediment-starved Glen Canyon and Marble Canyon reaches), following >1 yr of high (sediment-exporting) flows (Hazel et al. 1999, Schmidt et al. 1999a). This demonstrates that the GCD-EIS formula for sediment management through controlled flooding (floods every 5-10 yr) is at least partially appropriate. Ultimately, a mixed strategy of short-term and long-term BHBFs may be most appropriate for managing sediment flux.
The Grand Canyon Monitoring and Research Center continues to sponsor research and monitoring to develop a sediment budget for the Colorado River, focusing on the Marble Canyon Reach. Recent work suggests that considerable error in the measurement of suspended sediment concentrations in tributaries and the mainstem does not allow the development of a budget to address decadal-scale
changes in sand storage (Topping et al. 2000a). However, as the time scale of the budget decreases (annual, seasonal, weekly) the effect of measurement error on the difference between inputs and outputs relative to available storage space declines. This increases the accuracy of sediment storage estimates derived from a budget, making it a useful tool to evaluate particular management events (e.g., artificial floods occurring on day-to-week time scales).
The long-term prognosis for predicting the effects of management activities on sediment flux in Grand Canyon is good, based on the knowledge and tools being developed from the physical science research program. Sediment inputs from major tributaries have been modeled (Paria: Topping 1997), are currently being modeled (LCR: D. Topping, USGS, Denver, Colorado, work in progress), and inputs from ungaged tributaries are being estimated and validated (T. Melis, Grand
Canyon Monitoring and Research Center, Flagstaff, Arizona, personal communication). Estimations of storage potential in eddies (J. Hazel, M. Kaplinski, and R. Parnell, Northern Arizona University, Flagstaff, Arizona), main-channel pools (T. Randle, BOR, Lakewood, Colorado), and channel margin environments (J. Smith, USGS, Denver, Colorado) are ongoing and will be used to revise the storage functions used in GCM or other models. Hydrodynamic modeling (Cluer 1997, Wiele 1998) of eddy and main-channel environments will continue to provide insights on resuspension and deposition rates as affected by changes in flow, sediment concentrations, and grain size. Results from detailed modeling can be summarized and used in coarser scale system-wide models such as GCM to drive rates of erosion and deposition (S. Wiele, USGS, Lakewood, Colorado,USA, unpublished data). Historical analyses of sediment deposition patterns (J. Schmidt, Utah State University, Logan, Utah) have been completed and are underway to provide a long-term perspective and to help validate model predictions. A recently completed peer-review evaluation of the physical monitoring program will help to ensure that monitoring is sufficient to detect changes in sediment resources resulting from changes in GCD operations.
Extreme and costly policy options (major flow changes and temperature modification) in Table 2 have been suggested to improve or restore favorable physical habitat conditions (i.e., temperature, turbidity) for native fishes. These options have
potentially large negative impacts on power values, recreational rafting, and recreational fishing.
Perhaps the most important finding from GCM to date is that it would be extremely risky to equate physical habitat restoration with ecological and population restoration, as has been done by proponents of such restoration (Naiman et al. 1995). GCM indicates that there are three main, but conflicting, types of effects from such physical changes:
Thus, enhancing effects in type (1) will be offset to some degree by the largely negative trophic effects (2)-(3). Our inability (based on existing data) to predict the quantitative net balance of these effects leads to the rows of question marks (extreme uncertainties) in Table 2.
It might be argued that the reason we need to admit such extreme uncertainty about native fish responses in GCM is that we simply have not modeled the physiology and behavior of these species in enough detail. Perhaps emergent population effects would be more clearly demonstrated by using methods such as individual-based models (Van Winkle et al. 1993, 1996, Castleberry et al. 1996) to track cumulative physical and trophic effects at finer space-time scales. Although we suspect that these approaches would fail badly, mainly because of difficulties in predicting meso-scale spatial movement (dispersal, migration) patterns and in linking such movement to predation risk, we certainly cannot reject them out of hand. In fact, we recommend that they at least be tried, using the physical and trophic space-time “template” provided by GCM. The cost of failure for such an exercise is certainly minor compared to the potential costs and damages of proceeding with future policy changes on the basis of unsupported arguments about improving physical habitat factors.
Seasonally warmed backwater habitats (created by sand deposition in eddies) are a central concern of the GCD-EIS, and are considered by some ecologists to be nutrient and biodiversity “hotspots” for marsh vegetation, some bird species, and possibly native fishes (Stevens et al. 1995, Valdez and Carothers 1998, Parnell et al. 1999). Potentially serving as warmwater biological oases in the otherwise oligotrophic Colorado River downstream from the Paria River, they may be particularly essential for native sucker species, whose juveniles disperse widely over the system from tributary spawning areas and are sampled mainly in backwaters. However, some Grand Canyon fish researchers dispute the significance of backwaters to native fish recruitment. High densities of some native fish species have been measured in some backwaters, but these observations are often coupled with observations of high densities of exotic
competitor and predator species. Backwater area has decreased through aggradation since the rejuvenating high flows of 1983 (L. E. Stevens, unpublished data), decreasing the opportunity to evaluate their importance as fish nursery habitats. At present, the physical extent of backwaters is trivial relative to complex nearshore habitat in the mainstem or other off-channel sources (e.g., ponded tributary mouths).
Prediction of changes in backwater areas under alternate flow and sediment supply regimes is problematic because they are typically associated with dynamic, sometimes unstable, geomorphic features that vary as a function of changes in sand storage and vegetative succession. Large, persistent backwaters are commonly floored with tributary-derived silt and clay particles that change the fate of backwater rejuvenation and plant succession during and after high flows
(Stevens et al. 1995). Simulating these complex dynamics is beyond the scope of GCM, which focused on predictions over the entire ecosystem. We therefore entered reach-scale data on counts and size of backwaters from air photographs into GCM; based on these data, we assume broad relationships between accessible backwater area and stage/flow (generally accessible and wetted backwater area increases at first with stage, then falls dramatically at higher stages). These
relationships may be adequate for prediction of responses to modest policy changes within the range of recent experience (diurnal flow changes, moderate beach/habitat building floods). However, we are grossly uncertain about the net dynamic effects, from both physical and biological viewpoints, of more extreme policy changes such as seasonally adjusted steady flows that attempt to provide a more natural hydrograph. We do not simulate either the detailed space-time dynamics of backwater community change in response to changes in flow (e.g., effect of flood scouring events), or the physical dynamics of backwater formation and maintenance. Complex fine-scale hydrological and sediment movement processes create backwaters and define dynamic changes in return channel linkages to the main river, and we have been unable to find practical ways to model these dynamics at the reach or system scale. Future hydrodynamic/sediment models for single-eddy complexes (Cluer 1997, Wiele 1998) may improve understanding of physical changes associated with seasonal flow policies.
As noted earlier, we have been unable to reach consensus on even the direction of responses of several endangered native fish species to construction of GCD and to recent changes in diurnal water fluctuation policies. Although dedicated fisheries scientists have gathered masses of statistics on native fishes, little of this information has been analyzed in a fashion that addresses management questions. Existing sampling programs appear unable to detect population changes
much short of complete recruitment failure. Further, there has been a tendency to focus research directly on endangered species, when at least equal effort should be directed to understanding dynamic changes in some of their non-native predators and competitors, particularly brown trout, channel catfish, and carp.
This is clearly an unacceptable situation, especially considering how some of the most expensive proposals for change in water management (selective withdrawal structures for warming water, seasonally adjusted flows) are being made explicitly and solely to benefit native fishes. How did such a situation arise? Through the development of the fish component of GCM, discussions on the problems with historical fisheries sampling programs generally fell into one of three categories:
Existing tagging and mark-recapture abundance estimation programs may eventually provide a more sound basis for dealing with the first two problems, but thus far, the results from these programs have not been very encouraging. For example, humpback chub abundance estimates for the Little Colorado River over the last several years vary by a factor of 5, far more than the adult population size could possibly have varied, considering the longevity of the species.
The Grand Canyon Monitoring and Research Center will soon be undertaking a “Protocol Evaluation” of its fisheries research, with the objective of creating a monitoring program to detect changes in fish populations over time and to avoid administrative problems that have plagued past efforts. Several considerations are likely to improve this review:
Management of the Colorado River ecosystem exists in a perennial state of strabismus, with one eye focused clearly on economic exploitation and the other on maintenance of (or the appearance of) natural, wilderness-like conditions. Some AEAM workshop participants have expressed the expectation that GCM can help to define “optimum” water management policies for balancing conflicting objectives. The objectives to be balanced include the cost of foregone power revenues, maintenance of productive fisheries and bird populations in upper Canyon reaches, provision of usable beaches and flows for recreational rafting, protection and enhancement of native fishes, and protection of cultural resources.
Policy tests to date support this expectation only in relation to modest policy changes involving allowable diurnal variation in flow from GCD, and occasional beach/habitat-building flows. That is, for such policy changes, we can provide reasonable assessments of change in foregone power revenues, rainbow trout recruitment and fishing effort, and accumulation/loss of downstream beach habitats. We suspect that formal analysis of trade-offs related to allowable diurnal flow
variation will eventually show that the current MLFF (Modified Low-Fluctuating Flow) option is near optimum, with the caveat that minimum flow restrictions should be extended to limit sporadic low flows during weekends and holiday. Allowing very low flows for even one day per week probably does as much damage to aquatic invertebrate production as would diurnal desiccation, considering that these organisms have biomass response scales of months (Angradi and Kubly 1993).
However, our confidence in the benefits of more extreme policy options is low, particularly for physical habitat manipulations such as increasing water temperature, or recreating a natural annual flow regime (i.e., seasonally adjusted steady flows). There we see not only gross uncertainty about ecological responses, but also deep, and apparently irreconcilable, value conflicts: the “front end” capital costs of GCD modification are high, costs of power production will increase dramatically, and the recreational trout fishery and water bird/Peregrine Falcon bird community may be severely affected.
Severe costs and conflicts associated with extensive physical habitat restoration measures, along with uncertainty about the efficacy of such measures, may drive stakeholders to seek alternative, innovative methods to enhance native fish populations. Methods that have already been suggested include direct control techniques for exotic fishes (e.g., barriers in Bright Angel Creek to eliminate the main brown trout spawning run, attractant trapping/mechanical removal methods
for carp and channel catfish), and transplant programs to establish additional spawning populations of native fishes in apparently suitable areas not presently being used (e.g., humpback chub in tributaries other than the LCR). It is likely that other methods can be found if consensus is reached that gross restoration options are too risky.
From a purely scientific perspective, probably the most informative experiment that could be done in the near future in the Grand Canyon would be to introduce warm surface waters into the system from Lake Powell. However, such an experiment would have substantial front-end cost (> U.S.$15 million for initial construction; Bureau of Reclamation 1999), a risk of causing negative impacts on native species by stimulating exotic predator/competitor populations, and might fail to produce clear response data in view of inadequacies in the present fish monitoring programs and baseline data for pre- and post-treatment comparisons. We recommend that such an experiment be delayed until monitoring programs have been very substantially revised and have been in place long enough to provide a good baseline for comparisons.
We are also hesitant to recommend additional experimentation with diurnal flow limits at this time, for two reasons. First, as for thermal-regime management, it is unlikely that even qualitative effects of such regimes on native fishes can be measured. Second, we consider the evidence to be very clear that MLFF has substantially improved recruitment to the rainbow trout fishery, and primary/secondary production in the Glen Canyon Reach as well. The impacts of these changes have yet to be fully appreciated; e.g., rainbow trout recruitment rates may now be high enough to substantially affect some components of the invertebrate food base and prevent production of trophy-size fish. MLFF should be continued at least long enough for trout production to stabilize. There could be some “tinkering” with diurnal flow ramping rates and flow maxima (we suspect that biologists have been more conservative than necessary in asking for relatively slow ramping), if substantial economic benefits can be demonstrated for allowing these modifications.
This leaves two main categories of management experiments that require serious consideration by the Glen Canyon Dam Adaptive Management Program. First, experimental beach/habitat-building flows (BHBFs) should be continued, with particular emphasis on evaluating the impact on camping beaches, system-wide sand storage, and retention of fine-grained deposits on sandbars. Second, there should be concerted support for experimental tests of control techniques for exotic fish as a method for enhancing native fish species. Unfortunately, current institutional
barriers and legal constraint presently limit the likelihood of successful implementation of these experimental strategies, for reasons we will outline.
BHBFs were proposed as part of the GCD-EIS recommendations (BOR 1995); however, the Colorado Basin states objected on legal grounds to violation of the 1968 Colorado River Basin Project Act provision, which limits spills. The Department of Interior and Basin states reached an agreement by changing the timing of experimental floods from low reservoir storage years to years when reservoir releases in excess of power plant capacity are likely to be required for dam safety (high inflows coupled with a relatively full reservoir; Schmidt et al. 1999b). Based on this agreement, experimental floods in excess of power plant capacity must be initiated by “hydrologic triggering criteria,” which confines them to periods when a spill would probably be initiated for operational/dam safety reasons (May-June in high inflow years). From a scientific perspective, there are many problems with this arrangement. First, recent analyses of sediment transport in the Grand Canyon suggest that the residence time of fine-grained sediment delivered from tributaries is relatively short (Topping et al. 2000b), and mainstem floods may need to be timed to coincide with tributary floods to maximize retention of fine-grained deposits. However, under the current BHBF agreement and USFWS Biological Opinion, experimental floods are limited to the winter-spring period, and are prohibited during the summer monsoon season (July-September), when sediment delivery from tributaries is highest. Second, there is less control of GCD discharge before and following an experimental flood when the reservoir is high, because dam safety considerations must govern water releases. This adds a considerable source of avoidable variation into the system response to the BHBF, and to our ability to monitor the response. Third, the triggering criteria approach does not give scientists sufficient time to deploy equipment and personnel to monitor effects of the flood. Finally, because experimental floods will only occur in high inflow years when the reservoir is relatively full, it could be decades before another experimental flood is conducted under a relatively dry future climactic scenario.
Implementation of control techniques for exotic species may be difficult to initiate, because such activities apparently conflict with management objectives of Grand Canyon National Park. The Southwestern Willow Flycatcher (Empidonax trailii) is a neotropical migratory songbird that is on the verge of extirpation in upper Grand Canyon, where only one breeding pair remains. There is substantial scientific evidence that this federally endangered species has been declining because of brood parasitism by Brown-headed Cowbirds, Molothrus ater (Brown 1988, BOR 1995, Sogge et al. 1997). However, the trapping or killing of cowbirds, a native species whose populations have increased in response to increased livestock populations, is only now being initiated, despite repeated recommendations from concerned scientists over the past 20 years. Efforts to control non-native fish have similarly met with bureaucratic inertia, although recently, the National Park Service approved a proposal to evaluate control of channel catfish at the Colorado-LCR confluence. It is too early to tell whether recent park service initiatives are indicative of a more proactive attitude, or are simply a “blip” in a long-term trend of maximizing the appearance of unmanaged, wilderness-like conditions for a constituency largely composed of whitewater recreationists on commercial river trips. Other agencies play major roles as well: several recent USFWS Biological Opinions prohibit additional BHBFs until additional populations of endangered Kanab ambersnail (Oxyloma haydeni kanabensis) are established, but successful establishment criteria have not been defined. A shift in management toward more active strategies may substantially improve protection of some endangered species.
Institutional barriers pose the greatest threat to successful implementation of large-scale adaptive management experiments and contribute to current difficulties within the Grand Canyon Adaptive Management Program. Changes in the operation of Glen Canyon Dam have resulted in the transfer of benefits from one stakeholder group to another, and will continue to do so. Restricted daily flow fluctuations, BHBFs, and more costly restoration options (e.g., seasonally adjusted steady flows) result in the transfer of benefits from water and power interests to those representing ecological and recreational concerns. The rate at which this transfer occurs, by changes in operations, should be driven by societal values as well as our current understanding (or ability to understand through experimentation) of system responses. Water and power interests believe that a significant transfer of benefits has already occurred through reduced daily flow fluctuations beginning in 1990 (currently about U.S.$6 million/yr in lost power revenues under MLFFA; Harpman 1999a), the 1996 BHBF ($2.5 million in lost power revenues plus $1.5 million in research costs; Harpman 1999b), and through support of current research and monitoring activities and GCMRC (>$9.6 million in fiscal year 2000). Stakeholders representing ecological and recreational values believe that the rate of transfer of benefits has not been fast enough. From their perspective, the Grand Canyon ecosystem has been subsidizing an annual benefit of about U.S.$70 million worth of power from Glen Canyon Dam (Harpman 1999a), in addition to the benefits from supplying water for irrigation and urban development since 1963. Undoubtedly, the desired rate of transfer of benefits for different stakeholders depends on their individual value systems.
The second factor that should determine the rate of transfer of benefits is our understanding of how the system will respond to management actions, or at least our ability to measure this response through experimental management and monitoring. As discussed, our current understanding of factors that limit recruitment of native fish species in Grand Canyon is inadequate to prescribe
changes in dam operations, and current monitoring probably will not detect population changes resulting from experimental management. In addition, these restoration measures have the potential to backfire and stimulate the recruitment of exotic fishes, potentially to the detriment of endangered native fish. Water and power interests are well aware of these facts, and therefore view the experimental implementation of proposed restoration strategies as inappropriate or premature. For lower cost GCD management options, such as small changes to daily flow fluctuations (reducing weekend low flows), or BHBFs, our current understanding and monitoring abilities are sufficient to justify their implementation in a scientifically defensible experimental manner (at least for most resource components). However, since the 1996 BHBF, water and power interests and the USFWS have been resistant to implementing experimental floods in months outside of those determined though the hydrological triggering criteria, in spite of scientific evidence suggesting that late-summer floods may be more efficient for sediment management. In addition, water and power interests have attempted to constrain the spatial extent of monitoring and research to the immediate river corridor, and have resisted studies in Lake Powell and major tributaries below GCD, despite their obvious implications for interpretation of the effects of GCD operations. The position of water and power interests on small changes in GCD operations and research/monitoring planning thus seems illogical, but is easier to understand considering concerns about the premature implementation of more extreme operational changes. Of course, slowing or failure of the AEAM program may be economically advantageous to water and power interests, an issue that must be recognized as a further institutional barrier to the program’s success.
What can be done to ease the gridlock that is beginning to surround the Grand Canyon Adaptive Management Program?
We believe that implementation of these recommendations should be acceptable to most stakeholders. Water and power interests should feel that the rate of transfer of benefits is more in line with current scientific understanding. This, in conjunction with the possibility of continued research on fluctuating flows, may relax current constraints and attitudes on BHBFs and research and monitoring. Effective implementation of BHBFs will provide some immediate ecological and recreational benefits (Webb et al. 1999), and establishment of a long-term monitoring program will allow for a scientifically defensible evaluation of more costly restoration options in the foreseeable future.
The AEAM modeling process described in this paper has been useful for identifying information gaps and for prioritizing experimental management options and monitoring requirements in the Grand Canyon. However, institutional barriers need to be resolved before the results of this exercise can be used to improve the Adaptive Management Program. Under the current regime of institutional arrangements and attitudes, future experiments are likely to be designed by a combination of legal and political constraints, coupled with the subjective and selective use of scientific information to support the agendas of the various stakeholders involved in the adaptive management process. We admit that we do not understand all the causes or solutions to such problems, and have provided but one of many interpretations in this paper. We invite readers to provide their perspectives, using the response feature of Conservation Ecology. The successful application of large-scale adaptive management experiments is challenging under the best of circumstances (Walters 1997). We urge managers to consider these challenges and the ideas presented in this paper in future decisions of the Glen Canyon Dam Adaptive Management Program.
Responses to this article are invited. If accepted for publication, your response
will be hyperlinked to the article. To submit a comment, follow
this link. To read
comments already accepted, follow this link.
We gratefully acknowledge the many scientists and managers who shared their ideas and opinions, data, and models in the development of the Grand Canyon conceptual model. Special thanks to Ted Melis, and Barbara Ralston at the Grand Canyon Monitoring and Research Center. We thank Randall Peterson for his insightful comments on the institutional challenges facing the Grand Canyon Adaptive Management Program. Funding for this work was provided by the U.S. Bureau of Reclamation through the GCMRC. Contributors to the conceptual model are listed below.
Arizona Game and Fish Department: Tim Hoffnagle, Ted Mckinney, Bill Persons, Larry Riley, Dave Speas; U.S. Bureau of Reclamation: David Harpman, Bruce Moore, Randall Peterson, Tim Randle; Glen Canyon Recreation Area: Norman Henderson, John Spence; Grand Canyon Monitoring and Research Center: Susan Huefftle, Jeanne Korn, Ruth Lambert, Ted Melis, Barbara Ralston, Bill Vernieu, Mike Yard; National Park Service: Bill Jackson, Robert Winfree; Northern Arizona University: Joseph Hazel, Matt Kaplinski, Rod Parnell, Joseph Shannon; U.S. Fish and Wildlife Service: Owen Gorman, Robert Bramblett, Debra Bills; U.S. Geological Survey: Mark Anderson, Jim Bennett, David Topping, Stephen Wiele; Other agencies/independent: Wayne Cook, Upper Colorado River Commision; Michael Douglas, Arizona State University; David Foster, Marble Canyon Guides; Clayton Palmer, Western Area Power Authority; Andre Potochnik, Grand Canyon River Guides; Richard Valdez, SWCA Inc.; Micheal Yeats, Hopi Tribe.
Adler, T. 1996. Healing waters: Flooding rivers to repent for
the damage done by dams. Science News 150:188-189.
Anderson, L. S., and G. A. Ruffner. 1988. Effects of the
post-Glen Canyon Dam flow regime on the old high water zone plant
community along the Colorado River in Grand Canyon. National Technical
Information Service PB88-183504/AS.
Angradi, T. R., and D. M. Kubly. 1993. Effects of atmospheric
exposure on chlorophyll a, biomass and productivity of the epilithon of a
tailwater river. Regulated Rivers: Research and Management 8:345-358.
Anonymous. 1997. Glen Canyon Dam beach/habitat building
flow. Abstracts and Executive Summaries. Report available from Grand Canyon Monitoring
and Research Center, Flagstaff, Arizona, USA.
Beverton, R. J., and S. J. Holt. 1957. On the dynamics of
exploited fish populations. Fisheries Investment. Series 2. Volume
19. U.K. Ministry of Agriculture and Fisheries, London, UK.
Bishop, R. C., K. J. Boyle, M. P. Welsh, R. M. Baumgartner, and
P. C. Rathbun. 1987. Glen Canyon Dam releases and downstream recreation: An
analysis of user preferences and economic values. Glen Canyon Environmental
Studies Report 27/87. Hagler Bailly Consulting, Madison, Wisconsin,
USA. National Technical Information Service (NTIS, Springfield, Virginia)
PB88-183546/AS.
Bishop, R. C., C. A. Brown, M. P. Welsh, and K. J. Boyle.
1989. Grand Canyon recreation and Glen Canyon Dam operations: An economic
evaluation. In K. J. Boyle and T. Heekin, editors. Benefits
and costs in natural resource planning. Interim Report 2,
W-133. Department of Agricultural and Resource Economics, University of Maine, Orono, Maine, USA.
Blinn, D. W., J. P. Shannon, L. E. Stevens, and J. P. Carter.
1995. Consequences of fluctuating discharge for lotic
communities. Journal of the North American Benthological Society 14:233-248.
Boyle, K. J., M. P. Welsh, and R. C. Bishop. 1993. The role of
question order and respondent experience in contingent-valuation
studies. Journal of Environmental Economics and Management
25 (1, July 1993):80-99.
Brown, B. T. 1988. Breeding ecology of a Willow Flycatcher
population in Grand Canyon, Arizona. Western Birds 19:25-33.
Brown, B. T., and M. W. Trossett. 1989. Nesting-habitat
relationships of riparian birds along the Colorado River in Grand Canyon,
Arizona. Southwestern Naturalist 34:260-270.
Bureau of Relcamation. 1995. Operation of Glen Canyon Dam
Colorado River Storage Project, Arizona. Final Environmental Impact
Statement. U.S. Department of the Interior, Bureau of Reclamation,
Upper Colorado Division, Salt Lake City, Utah, USA.
Bureau of Reclamation. 1999. Glen Canyon Dam modifications to
control downstream temperatures. Plan and Draft Environmental
Assessment. U.S. Department of the Interior, Bureau of Reclamation,
Upper Colorado Division, Salt Lake City, Utah, USA.
Castleberry, D. T., J. J. Cech Jr., D. C. Erman, D. Hankin,
M. Healey, G. M. Kondolf, M. Mangel, M. Mohr, P. B. Moyle, J. Nielsen,
T. P. Speed, and J. C. Williams. 1996. Uncertainty and instream flow
standards. Fisheries 21(8):20-21.
Cluer, B. L. 1997. Eddy bar responses to the sediment dynamics
of pool-riffle environments. Report prepared for Bureau of Reclamation, Glen
Canyon Environmental Studies Office, Flagstaff, Arizona, USA.
Collier, M. P., R. H. Webb, and E. D. Andrews.
1997. Experimental flooding in Grand Canyon. Scientific American 276:82-89.
Deriso, R. B. 1980. Harvesting strategies and parameter
estimation for an age-structured model. Canadian Journal of Fisheries and Aquatic
Science 37: 268-282.
Graf, J. B. 1995. Measured and predicted velocity and
longitudinal dispersion at steady and unsteady flow, Colorado River,
Glen Canyon Dam to Lake Mead. Water Resources Bulletin 31:265-281.
Haden, A., D. W. Blinn, J. P. Shannon, C. O'Brien, and
K. P. Wilson. 1997. Benthic ecology of the Colorado River
system through the Colorado Plateau region of the southwestern United States. Northern Arizona University, Flagstaff, Arizona, USA.
Harpman, D. A. 1999a. Assessing the short-run economic
cost of environmental constraints on hydropower operations at Glen Canyon
dam. Land Economics.
Harpman, D. A. 1999b. Origins of the 1996 controlled
flood in Grand Canyon. In R. H. Webb, J. C. Schmidt, G. R. Marzolf, and
R. A. Valdez, editors. The controlled flood in Grand Canyon. American
Geophysical Union. Geophysical Monograph 110.
Harpman, D. A., and A. S. Rosekrans. 1996. Modeling hourly
operations at Glen Canyon Dam Colorado River storage project, Arizona.
U.S. Department of the Interior, Bureau of Reclamation, GCPS09 version 1.0.
Hazel, J. E. Jr., M. Kaplinski, R. A. Parnell, M. Manone, and
A. Dale. 1999. Sediment storage repsonses to controlled flooding,
Colorado River in Grand Canyon.In R. H. Webb, J. C. Schmidt,
G. R. Marzolf, and R. A. Valdez, editors.The controlled flood in
Grand Canyon. American Geophysicists Union Monograph 110.
Hereford, R., H. C. Fairlye, K. S. Thompson, and J. R. Balsom.
1993. Surficial geology, geomorphology, and erosion of archeologic sites along
the Colorado River, eastern Grand Canyon, Grand Canyon National Park,
Arizona. U.S. Geological Survey, Open-File Report 93-517.
Hilborn, R., and C. Walters. 1992. Quantitative fisheries
stock assessment and management: choice, dynamics, and uncertainty. Chapman
Hall, New York, New York, USA.
Holling, C. S., editor. 1978. Adaptive environmental
assessment and management. John Wiley, New York, New York, USA.
Kearsely, L. H., J. C. Schmidt, and K. D. Warren. 1994. Effects
of Glen Canyon Dam on sand deposites used as river campsites in the Grand
Canyon of the Colorado River, U.S.A. Regulated Rivers: Research and
Management 9:137-149.
Kearsley, L., and K. Warren. 1992. River campsites in Grand
Canyon National Park: Inventory and effects of discharge on campsite size and
availability. National Park Service, in cooperation with Glen Canyon
Environmental Studies. Flagstaff, Arizona, USA.
McQueen, D. J., J. R. Post, and E. L. Mills. 1986. Trophic
relationships in freshwater pelagic ecosystems. Canadian Journal of
Fisheries and Aquatic Science 43:1571-1581.
Myers, R. A., and N. J. Barrowman. 1996. Is fish recruitment
related to spawner abundance? Canadian Journal of Fisheries and Aquatic
Science 52:223-232.
Naiman, R. J., J. J. Magnuson, D. M. McKnight, and J. A. Stanford,
editors.1995. The freshwater imperative: a research agenda. Island
Press, Washington, D.C., USA.
Nathonson, M. N. 1980. Updating the Hoover Dam
Documents. U.S. Government Printing Office, Denver, Colorado, USA.
NRC (National Research Council). 1996. River resourse
management in the Grand Canyon. National Academy Press, Washington, D.C., USA.
Oksanen, L., S. Fretwell, J. Arruda, and P. Niemela.
1981. Exploitation of ecosystems in gradients of primary
productivity. American Naturalist 118:240-261.
Orvis, C. J., and T. J. Randle. 1987. Sediment transport and
river simulation model. U.S. Department of the Interior, Bureau of
Reclamation, NTIS PB88-183413/AS.
Parnell, R. A., J. B. Bennett, and L. E. Stevens.
1999. Mineralization of riparian vegetation buried by the 1996
controlled flood. Pages 225-240 in R. H. Webb, J. C. Schmidt,
G. R. Marzolf, and R. A Valdez, editors. The controlled flood in
Grand Canyon. American Geophysical Union Monograph 110, Washington, D.C., USA.
Power, M. E. 1990. Effects of fish in river food
webs. Science 250:811-814.
Power, M. E. 1992a. Top-down and bottom-up forces in
food webs: do plants have primacy? Ecology 73:733-746.
Power, M. E. 1992b. Habitat heterogeneity and the
functional significance of fish in river food webs. Ecology
73:1675-1688.
Randle, T. J., and E. L. Pemberton. 1987. Results and
analysis of STARS modeling efforts of the Colorado River in Grand Canyon.
U.S. Department of the Interior, Bureau of Reclamation, NTIS PB88-183421/AS.
Rubin, D. M., J. M. Nelson, and D. J. Topping. 1998. Relation
of inversely graded deposits to suspended-sediment grain-size evolution during
the 1996 flood experiment in Grand Canyon. Geology 26:99-102.
Schaefer, M. 1997. Merging ecosystem science and adaptive
management. Glen Canyon Dam Beach/Habitat-Building Flow
Symposium. Abstracts and Executive Summaries. Grand Canyon Monitoring
and Research Center, Flagstaff, Arizona, USA.
Schmidt, J. C., E. D. Andrews, D. L. Wegner, and D. T. Patten.
1999b. Origins of the 1996 controlled flood in Grand Canyon. In
R. H. Webb, J. C. Schmidt, G. R. Marzolf, and R. A. Valdez, editors. The
controlled flood in Grand Canyon. American Geophysical Union, Geophysical
Monograph 110.
Schmidt, J. C., P. E. Grams, and M. F. Leschin. 1999a.
Variation in the magnitude and style of deposition and erosion in three long
(8-12 km) reaches as determined by photographic analysis. In R. H. Webb,
J. C. Schmidt, G. R. Marzolf, and R. A. Valdez, editors. The
controlled flood in Grand Canyon. American Geophysical Union,
Geophysical Monograph 110.
Schmidt, J. C., R. H. Webb, R. G. Marzolf, R. A. Valdez, and
L. E. Stevens. 1998. Science and values in river restoration in the Grand
Canyon. BioScience 48:735-747.
Schnute, J. 1987. A general fishery model for a size-structured
fish population. Canadian Journal of Fisheries and Aquatic Science
44: 924-940.
Shannon, J. P., D. W. Blinn, P. L. Benenati, and K. P. Wilson.
1996. Organic drift in a regulated desert river. Canadian Journal of
Fisheries and Aquatic Science 53: 1360-1369.
Sih, A., P. Crowley, M. McPeek, J. Petranka, and K. Strohmeier.
1985. Predation, competition, and prey communities: a review of field
experiments. Annual Review of Ecology and Systematics 16:269-311.
Sih, A., and D. E. Wooster. 1994. Prey behavior, prey
dispersal, and predation impacts on stream prey. Ecology 75:1199-1207.
Sogge, M. K., T. J. Tibbitts, and J. R. Petterson. 1997. Status
and breeding ecology of the Southwestern Willow Flycatcher in the Grand
Canyon. Western Birds 28:142-157.
Stevens, L. E. 1976. Insect production on native and introduced
dominant plant species. Pages 146-154 in S. W. Carothers and
S. W. Aitchison, editors. An ecological survey of the riparian
zone of the Colorado River between Lees Ferry and the Grand Wash Cliffs, Arizona. National Park
Service Colorado River Research Series Technical Report Number10, Grand Canyon.
Stevens, L. E. 1985. Invertebrate herbivore community
dynamics on Tamarix chinensis Loueiro and Salix exigua
Nuttall in the Grand Canyon, Arizona. Thesis. Northern Arizona
University, Flagstaff, Arizona, USA.
Stevens, L. E., K. A. Buck, B. T. Brown, and N. C. Kline.
1997a. Dam and geomorphological influences on Colorado River waterbird
distribution, Grand Canyon, Arizona, USA. Regulated Rivers: Research and
Management 13:151-169.
Stevens, L. E., J. C. Schmidt, T. J. Ayers, and B. T. Brown.
1995. Flow regulation, geomorphology, and Colorado River marsh
development in the Grand Canyon, Arizona. Ecological Applications 5:1025-1039.
Stevens, L. E., J. P. Shannon, and D. W. Blinn. 1997b.
Colorado River benthic ecology in Grand Canyon, Arizona, USA: dam, tributary,
and geomorphological influences.Regulated Rivers: Research and
Management 13:129-149.
Stevens, L. E., and G. L. Waring. 1988. Effects of post-dam
flooding on riparian substrates, vegetation, and invertebrate populations in
the Colorado River corridor in Grand Canyon. National Technical Information
Service PB88-183488/AS.
Strong, D. R. 1992. Are trophic cascades all wet?
Differentiation and donor-control in speciose ecosystems. Ecology 73:747-754.
Topping, D. J. 1997. Physics of flow, sediment transport,
hydraulic geometry, and channel geomorphic adjustment during flash
floods in the ephemeral river, the Paria River, Utah and Arizona.
Dissertation. University of Washington, Seattle, Washington, USA.
Topping, D. J., D. M. Rubin, J. M. Nelson, P. J. Kinzel, and
I. C. Corson. 2000b. Colorado River sediment
transport. Part 2: Systematic bed-elevation and grain-size effects of sand supply limitation. Water
Resources Research 36:543-570.
Topping, D. J., D. M. Rubin, and L. E. Vierra. 2000a.
Colorado River sediment transport. Part 1: Natural sediment supply
limitation and the influence of Glen Canyon Dam. Water Resources Research36:515-542.
Valdez, R. A., and S. W. Carothers. 1998. The aquatic
ecosystem of the Colorado River in Grand Canyon. Report prepared
for the Bureau of Reclamation, Salt Lake City, Utah. S. W. Carothers
and Associates, Inc., Flagstaff, Arizona, USA.
Valdez, R. A., and R. A. Ryel. 1997. Life history and ecology
of the humpback chub in the Colorado River in Grand Canyon, Arizona. Pages 3-32
in C. van Riper, III and E. T. Deshler, editors. Proceedings of the
Third Biennial Conference of Research on the Colorado
Plateau. National Park Service Transactions and Proceedings Series NPS/NRNAU/NRTP-97-12.
Van Winkle, W., H. I. Jager, and B. D. Holcomb. 1996. An
individual-based instream flow model for coexisting populations of
brown and rainbow trout. EPRI (Electrical Power Research Institute)
Interim Report TR-106258.
Van Winkle, W., K. A. Rose, K. O. Winemiller, D. L. DeAngelis,
S. W. Christensen, R. G. Otto, and B. J. Shuter. 1993. Linking life history
theory and individual-based modeling to compare responses of different fish
species to environmental change. Transactions of the American Fisheries
Society 122:459-466.
Walters, C. J. 1986. Adaptive management of renewable
resources. McMillan, New York, New York, USA.
Walters, C. J. 1994. Use of gaming procedures in evaluation of
management experiments. Canadian Journal of Fisheries and Aquatic
Science 51:2705-2714.
Walters, C. J. 1997. Challenges in adaptive management of
riparian and coastal ecosystems. Conservation Ecology
[online]1(2):1. Available from the Internet. URL: http://www.consecol.org/vol1/iss2/art1.
Walters, C. J., and F. Juanes. 1993. Recruitment limitation as
a consequence of natural selection for use of restricted feeding habitats and
predation risk taking by juvenile fishes. Canadian Journal of Fisheries and
Aquatic Science 50:2058-2070.
Walters, C. J., and J. Korman. 1999. Linking recruitment to
trophic factors: revisiting the Beverton-Holt recruitment model from a life
history and multispecies perspective. Reviews in Fish Biology and
Fisheries 9:1-16.
Webb, R. H., J. C. Schmidt, G. R. Marzolf, and R. A. Valdez,
editors. 1999. The controlled flood in Grand Canyon.
American Geophysical Union, Geophysical Monograph 110.
Welsh, M. P., R. C. Bishop, and M. L. Phillips.
1999. Valuing Grand Canyon riparian resources. Report submitted to Grand Canyon
Monitoring and Research Center, Flagstaff, Arizona, USA.
Wiele, S. M. 1998. Modeling of flood-deposited sand
distributions in a reach of the Colorado River below the Little
Colorado River, Grand Canyon, Arizona. U.S. Geological Survey
Water-Resources Investigations Report 97-4168.
Wiele, S. M., and E. R. Griffin. 1997. Modifications to a
one-dimensional model of unsteady flow in the Colorado River through the Grand
Canyon, Arizona. U.S. Geological Survey Water-Resources
Investigations Report 97-4046.
Wiele, S. M., and J. D. Smith. 1996. A reach-averaged model of
diurnal discharge wave propagation down the Colorado River through the Grand
Canyon. Water Resources Research 32(5):1375-1386.
Wooster, D. 1994. Predator impacts on stream benthic
prey. Oecologia 99:7-15.
Yard, M. D., G. A. Haden, and W. S. Vernieu.
1993. Photosynthetically available radiation (PAR) in the Colorado River: Glen and Grand
Canyon. Glen Canyon Environmental Studies Report, Flagstaff, Arizona,USA.
Average monthly diurnal discharge hydrographs for three reaches under the No Action and Modified Low Fluctuating Flow (MLFFA) alternatives, based on a GCD release volume of 1 million acre-feet. Solid lines denote the average monthly diurnal hydrograph generated during the on-peak demand period (Monday-Saturday), and dashed lines denote the hydrographs during off-peak periods (Sunday). The economic monthly value of power generated from GCD (in millions of 1996 U.S. dollars) under these alternatives are shown. Assuming a hydropower production cost of $1.80/MWh (Harpman 1998) results in a production cost of $875,000 (in 1996 dollars) under both alternatives in January and $890,000 in August. The river miles locations (downstream from GCD) of the hydrographs (reach midpoints) are shown in parentheses beside the reach names.
Potential storage relationships used in the GCM sediment budget for eddy, channel margin, and main-channel pool environments, and reach morphological statistics derived from aerial photo analysis.
Simulations of discharge, eddy and main-channel (MC) pool storage, and suspended sediment concentrations in the Furnace Flats reach between the LCR and Phantom Ranch (only data for the month of June are plotted). Eddy and MC pool storage is expressed as a fraction of the maximum storage potential in each of these environments.
Details of sediment budget computations and Lagrange tracking temperature model.
Sediment budget computations
For each reach, the sand transport component of the model proceeds as follows.
Lagrange estimation of downstream concentration profiles-temperature model
One of the most difficult computational problems in river ecosystems is to represent gains and losses of materials and energy suspended in the water column, as water moves rapidly downstream (e.g., detritus, drifting insects, temperature). We use a Lagrange "sampling" method to deal with such variables (Fig. 4). We think of taking a representative sample parcel of water entering the system each month, and following how concentrations will change in that parcel due to gains (from atmosphere, river bottom, tributaries) and losses (sinking, decomposition, heat loss) as it moves downstream. Dynamic change along each Lagrange sample track is assumed to follow relatively simple linear dynamics (dx/dt = a -bx, where a is the input rate, b is the loss rate, and x is reset at each at the time when the sample parcel passes each tributary input point) for which we can obtain an analytical solution for downstream concentration changes.
The net result of processes effecting gains and losses to the sample parcel of water determines the output (concentration or temperature) at the downstream boundary of each reach in our simulation. The downstream concentration (Ci+1) is computed by the equation
Eq. A4.1 consists of three components:
Eq. A4.2 was derived by initially formulating the change in mass within a reach over time as a difference equation:
That is, the rate of change in mass or temperature over time (ΔM/Δt)
within a reach will be a function of the difference between the gains due to resuspension
(RW, a function of the resuspension rate and the surface it acts on, which is proportional to the wetted width) and the losses due to sinking (sWC, a function of the sinking rate, the
surface on which this process occurs, and the concentration, C). Note that C is a function of mass divided by the volume of water, and Eq. A4.2 is therefore a differential equation. If we solve this equation over the period t that it takes the water, moving at a velocity v to pass through a reach of length L (t = L/v) and replace any reference to mass in Eq. A4.2 with its concentration equivalent,C/A, where A is cross-sectional area, which is equal to the volume for a 1 foot (0.3 m) thick section of water, we get the solution for the concentration at the bottom of the reach (Ci+1) given by Eq. A4.1.
Comparison of predicted and observed mean monthly water temperatures in the Lees Ferry (reach number = 1), Furnace Flats (6), and Lower Canyon (11) reaches. Lake Powell was impounded in March 1963 and completely filled in 1982. Discrepancy between observed and predicted values during the first 10 years of reservoir filling was caused by higher GCD outflow temperatures that were not modeled in our simulation.
Equations used in algal primary production and biomass submodel.
To represent the complex space-time pattern of algal biomass and production that is likely to
result from diurnal production/dessication/turbidity interactions, we predict monthly
average algal biomass per area, B(r,d), for a set of 2-foot depth slices (contours), d (d = 1 represents the bottom area from the deepest point to 2 foot depth across the channel, etc.) in each reach, r. Mean production per area Pr is then assumed to be proportional to the area-weighted mean of these biomass densities: Pr = kΣdB(r,d)W(r,d)/ ΣdW(r,d), where W(r,d) is the cross-sectional width of depth slice d for a typical cross-section in reach r, and k is a production/biomass scaling parameter. On monthly time scales, we assume that average biomass will satisfy the balance relation production = mortality, but we assume that (1) mortality is inversely related to the proportion of time H(r,d) that site r,d is flooded (H(r,d) is the hours per day that site r,d is flooded/24), and (2) production can be limited by biomass at low biomasses, according to a saturating relationship of the form
where Pmax(r,d) is the maximum net production per unit biomass per day at site r,d; PA is a maximum primary production per unit area in sites where B(r,d) is high enough so that production rate is not limited by algal biomass. Taking the rate of biomass change to be
Where M is a base mortality rate per biomass per day for sites that are permanently flooded, we can predict mean B when dB/dt = 0 by setting P(r,d) = M/H(r,d):
Note here that the M/H mortality assumption causes mortality to double for each halving of H, e.g., mortality is 2M if dessication occurs for 12 h/d, 4H if it occurs for 18 h/d, etc. For low H or P, Eq. A6.3 predicts negative average biomass (daily mortality exceeds daily production for all B); in this case, we set B(r,d) = 0.
To apply the algal biomass prediction model (Eq. A6.3), we need to estimate proportions of time flooded H(r,d) and maximum daily production per biomass Pmax(r,d). The hydrology submodel provides hourly stages S(r,h) for each reach r and hour h of the day (h = 1…24), using results from the Wiele-Smith one-dimensional wave propagation model, and the sediment transport submodel provides mean 24-h turbidities by reach, from which we can calculate light extinction coefficients λr by reach. For each depth slice d, we estimate H(r,d) simply by summing the hours for which S(r,h)>d. Daily maximum primary production rate Pmax is taken to be proportional to the sum over daylight hours of depth-corrected hourly rates, including in the sum only those hours for which S(r,h)>d:
Note that the basic form of the biomass prediction relationship Eq. A6.3 is robust to alternative assumptions about how biomass is limited. For example, suppose we start with the assumption that P/B depends only on environmental factors (Eq. A6.4), such that there is no production/area limit, but that mortality rate increases with biomass. Then we would use the equilibrium of the rate equation dB/dt = PmaxB-MB2/H to provide an approximation to the mortality rate effect. At equilibrium for this model, PmaxB = MB2/H, implying that B = PmaxH/M, which is similar to Eq. A6.3 (B is proportional to PmaxH and inversely proportional to M), except that it does not predict a threshhold minimum for P,H below which B would be zero.
As with other trophic components of the model, a key issue is whether primary production exerts bottom-up control on production of herbivores, or whether, instead, it can be controlled through top-down grazing effects. We assume that persistent high biomass (mats) of forms like Cladophora implies bottom-up control, i.e., the benthic algal mat must not be subject to very high grazing rates (perhaps because of chemical defenses of the algae, or because grazing insects are prevented from feeding on open surfaces by high predation risk from fish). Extensive direct grazing would be obvious, in the form of patchiness in algal biomass at the scale of a few centimeters ("worm trails" and other grazing impact signals). Without such signals, we assume that algal production moves through the food chain mainly via (1) consumption of epiphytic diatoms growing on the macroalgae, and (2) detritus production and consumption of this detritus by insects that spend most of their time in protected microhabitats (e.g., web spinners under rocks). Detritus production per unit area is assumed to be proportional to primary production, and "instantaneous" downstream profiles of detritus concentration are predicted each week, using an exponential profiling procedure based on Lagrange tracking of water masses downstream while accounting for additions from the bottom (and side terrestrial sources), decomposition, and grazing removal rates.
Comparison of mean simulated light attenuation, and algal and benthos biomass by reach, using mean observed values (1993-1996).
Simulated long-term changes in algal and benthos biomass for three sample reaches: just below Glen Canyon Dam, just above Little Colorado River (Marble Canyon), and near Lake Mead (Lower Canyon). Note the exaggeration of interannual variation in downstream reaches, due to impacts of turbidity from tributaries.
Equations used in benthic insect production submodel.
Benthic insect biomass dynamics are represented by monthly difference equations at the reach spatial scale; no attempt is made to simulate biomasses by depth slices within reaches, because of the likelihood that movement processes (crawling, drifting, etc.) among slices are fast enough to prevent substantial slice-scale variation from developing over time. Also, benthos sampling data do not indicate clear trends in biomass with depth, except for substantial biomass reduction in diurnally dried varial zones (we assume zero production in these zones) and lower average biomass in deeper sites because more of these sites have unstable sand substrates.
For each invertebrate type s (grazer, detritovore) in each reach r, we update monthly (m) biomass density (g/m2 ash-free dry mass) Bsr(m) using the difference equation
where gsr(Fsr(m)) is a biomass growth function dependent on food density Fsr(m); and msr(m) is a mortality rate dependent on temperature, predator abundances, diurnal dessication, and (in extreme situations) turbidity. Also, between months of rising mean stage, B is "diluted" by assuming that animals rapidly spread over the wider river width available Between months of falling stage, animals along the drying river margin are assumed to die (rather than contribute to increases in biomass density B by moving to remaining wetted areas).
The biomass growth function gsr(Fsr(m)) was derived by thinking initially about filter feeders (dominant in most river reaches), and assuming that animals compete locally within and upon the substrate for limited delivery rates of detritus to that substrate. We assume that similar local "delivery" rate mechanisms apply to production of the epiphytic algae (diatoms) that appear to be the main food supply of grazers (macroalgae like Cladophora and Oscillatoria appear not to be grazed directly, or at least not enough to cause noticeable effects such as hedging or patchiness). Within the limited "grazing arena" at the substrate, we suppose that g has the product form efc, where c is the effective food concentration in the arena; f is the filtering/scraping rate (volume or area/time); and e is food conversion efficiency. The problem then is to predict c as a function of overall food concentration Fsr(m) in the environment and of exchange/production/loss processes between c and F. We assume that mixing processes result in dc/dt = MF - rMF - fB/V, i.e., to have input rate proportional to F with instantaneous rate M, nongrazing loss rate proportional to F with rate rM (for detritus, r represents the "resuspension" rate relative to the "sinking" rate M), and feeding loss rate fB/V, where f has units of volume per biomass per time, and V is the effective volume of the grazing arena. We then assume that c reaches equilibrium quickly with respect to B and F (on time scales of hours to days), so that we can solve for c by setting dc/dt = 0. Substituting this variable speed-splitting solution for c into the rate product efc finally results in the overall relationship:
Here, the hyperbolic decreasing term Fsr(m))/[rs + fBsr(m)/V] represents the fast variable solution for c (density of food locally available to animals immediately at the substrate where they are competing). Note that in the case of s = grazers, we think of Fsr(m) as proportional to macroalgae biomass density, so that it represents algal concentration on macrophyte growth sites not accessible to grazing due to predation risk or other factors.
To simplify the estimation of parameters in (A9.2), we directly specify only e, r, M, baseline equilibrium values F0, B0, and mortality rate m, and maximum biomass growth rate r0 at low densities (this growth rate is r0 = efF0/r - m). Substituting these "knowns" into (A9.1) and (A9.2), with B(t +1) = B(t) results in estimates of effective f and V. In fact, this method allows us to make arbitrary choices for M as well (only product MV appears at equilibrium, so changing M just rescales estimate of effective arena volume V), and to think of the "resuspension" fraction r as a way of representing concentrating mechanisms such as quiet backwaters that support some insect production even where overall water column concentrations of detritus F (or bottom concentrations of algae) would be too low to support any production.
Why assume the relatively complex competition function (A9.2) rather than assuming growth rates simply proportional to overall detritus or algae concentrations in or below the water column? First, all of the available data suggest that food supply is indeed important to benthic insect abundance (strong downriver gradients, etc.). However, if we simply assume that growth rate is proportional to overall food density Fsr(m), we end up predicting that g should be either large enough to always predict B(m + 1)>B(m), or always low enough so that B(m + 1)<B(m), i.e., we end up predicting either unlimited population growth or decline. In simple food limitation models, increase in B results in decrease in F and. hence, population-limiting feedback. But especially for F = detritus in a large, fast-flowing river, the relatively low benthic biomass simply cannot affect overall food concentrations significantly, even over substantial downstream distances. The "grazing arena" density effect (reduced food density in the immediate environment where animals feed) is actually a very parsimonious way to introduce food-mediated density dependence (and, hence, population regulation) into the model.
Mortality rate msr(m) is assumed to consist of two components, m0 + m1. We assume that the baseline "natural" rate m0 would occur in the absence of fish and bird predation, due to various physiological problems and to maturation/emergence. The predation rate m1 is assumed to vary on interannual time scales with abundances of fish, and is parameterized by assigning each vertebrate predator species a baseline proportional contribution to m (i.e., a component of m1) when the vertebrate species is at baseline (1993) abundance, such that m0 consists of overall m times whatever proportional contribution is not accounted for by modeled predators. Then m1 is varied over time in proportion to ratios of predator abundance to baseline predator abundance. This approach allows us to easily examine various hypotheses about top-down vs. bottom-up control of predation effects (to effect bottom-up control, we set the relative predator contributions to total m at low values to model the idea that predation rate has little additive effect on m; to model top-down control, we set the proportions so that most of m is directly accounted for by predators).
Equations used in riparian vegetation growth and competition
submodel.
Changes in relative biomass density Bp,r,d(t)
(with a 0-1 biomass scale per unit suitable habitat) for plant type
p in reach r, and cross-sectional depth (stage) slice
d are simulated, using the following discrete logistic equation
for time steps t of one year:
where Sprd(t) is the product of all monthly
survivals through flooding events and inappropriate water table levels
during year t;
s is a seeding input rate (biomass colonization rate); and the
logistic re
lative growth rate Gprd(t) is given by:
In this growth function, rp is an intrinsic rate of
biomass increase for plant type p, and the
akp represent competition coefficients (effect of
unit of biomass of plant type k on the growth rate and carrying
capacity for plant type p, app = 1). In practice,
for plant type definitions used in baseline simulations, the
competition coefficients have little effect; the plant types are
"segregated" in habitat use by strong survival effects
(Sprd) caused by assuming different tolerances or
preferences for height above the water table.
The water table height Wr(m) for each month
m is set as a simple average of the last month's water table
height and of the mean diurnal river stage
Dr(m) for each reach each month, as
That is, water table height is assumed to "track" changes in
river stage with a modest time delay, rising somewhat more slowly than
the water level and decaying with a lag of around one month during
periods of falling stage. In practice, this assumption has little
effect on predictions for most water management scenarios. For natural
system "replays", violent seasonal stage variations cause
much larger survival Sprd effects than would changes
in water table depth, and most managed-system scenarios do not involve
large month-to-month changes in mean stage
Dr(m).
Although these equations appear to give reasonable predictions of
biomass development and, hence, total reach-scale relative biomasses
for substrate types that are stable on time scales of decades (rock,
ancient elevated sand bars, boulder and cobble areas), they may
predict to rapid a change in total reach-scale biomass for water
management scenarios that cause sudden, substantial increases in
sandbar area near the present high-water line (e.g.,
"beach-building" floods of somewhat larger magnitude than
the 1996 experimental flood). That is, because the model is not
keeping separate account of each substrate area by "age" of
origin or deposition (a very complex data gathering and simulation
problem), it will "suddenly" assign biomasses
Bprd(t), predicted from past dynamics on
already established sandbars, to the newly deposited
area. Fortunately, this effect is relatively small in most scenarios,
especially because flows that can produce large, new sand are as also
cause a substantial "reset" of all
Bprd(t) in affected depth slices (flooding
survival effect).
User interface for specifying riparian vegetation parameters. Rough curves in red for each type are user-sketched functions for mortality vs. depth and time of flooding/desiccation. The brown-green coded table allows users to define substrate types upon which each vegetation type can grow.
Simulated abundance of hydroriparian (marsh and grass) and Tamarisk (salt cedar)-dominated communities in upper Granite reach. The natural system reference point prior to impoundment (1963) has little vegetation below seasonal high flow stage. The1982 point shows considerable development of shoreline marsh and salt-cedar communities from 1963 until just prior to the1983-1984 floods, and the 1990 point shows virtually complete recovery of these communities within 15 years after those floods.
Equations used in vertebrate indicator populations submodel.
To simplify the following presentation of population dynamics relationships, we supress subscripts for reach and species. It is to be understood that all age-structure accounting relationships (for animals age 1 yr and older) are done at system-year scale (once per year for each species), and all recruitment relationships (egg/hatchling to age 1 yr) at reach-month scale.
The age-structure population dynamics accounting is based on the Deriso(1980)-Schnute (1987) delay-difference equation structure, which is used widely in fisheries assessment (see its derivation in Hilborn and Walters 1992). For animals age 1 yr to an age at maturity k, numbers at each age are propagated using a simple survival relationship N(a + 1,t< + 1) = SjN(a,t)
where Sj is an annual juvenile survival rate. For age k and older animals, we propagate total numbers N (summed over all ages, ignoring age-specific differences in survival rate) and adult biomass B using the delay-difference relations:
where t is time in years; Sa is adult annual survival rate (constant except for harvesting/control effects); R(t + 1) is age k recruitment in number of animals; A, ρ are Ford-Brody body growth model parameters; and wk is mean body weight (mass) at maturity.
It is not necessary to propagate these equations at reach spatial scale because we do not assume reach-specific differences in age 1+ growth and survival rates (except for time-varying harvest effects on Sa for rainbow trout in the reach just below Glen Canyon dam, where most of the rainbow population is found). The age 1 numbers entering the juvenile age accounting each year (leading at age k to total recruits R) are calculated as a sum, over reaches, of recruitment rates by reach.
Adults using each reach (a proportion of N,B based initially on historical data and then updated in relation to simulated recruitment success by reach over years) are assumed to produce eggs/hatchlings E(t) proportional to biomass, E(t) = eB(t) where e = eggs/adult biomass. Derivations in Walters and Korman (1998) imply that we can predict the number of age-1 recruits resulting from E(t), while accounting for monthly changes in predation risk related to food supply and growth, by a Beverton-Holt (1957) function of the form:
where Segg is egg survival rate, assumed to be constant; m is month of age (after hatching) m = 1…12; vm is relative vulnerability of m-month-old juveniles to predation; Sm(t) is maximum (low-density) survival rate over the month; K1,K2 are scaling constants that depend on units of measurement (see below); P(m) is an index of total predation risk per time foraging; F(m) is a weighted (by diet composition) index of food density; Hr(m) is a function defining relative (0-1) variation in the risk ratio effect (P/F effect on survival) with changes in physical habitat factors; and Hf(m) is a function defining relative (0-1) variation in usable foraging habitat (foraging arena size) with changes in physical habitat factors.
There are two key components in (A13.3): trophic linkage to predation risk and food availability via the risk ratio P(m)/F(m), and linkage to physical habitat factors that affect both predation risk and food competition via the habitat functions Hr and Hf.
The P and F functions are weighted sums over predators and food types of predators, and food-specific relative risks/opportunities. In initializing each simulation for baseline year 1993, we scale these functions so that P = 1, F = 1 if predator and food abundances identical to 1993 values reoccur in other simulation years. Thus, for example, if we have assumed that a particular predator accounts for 20% of the juvenile mortality in the 1993 baseline situation, we take its contribution to P in other years to be 0.2B(t)/B(1993), where B(t) is predator biomass in year t. Contributions to F are calculated the same way. We attempted a spreadsheet trophic modeling exercise to see if we could replace such relative predation and feeding rate calculations with dimensional mortality rate parameters based on absolute estimates of predator abundances, feeding rates, and diet compositions. This exercise revealed really discouraging gaps in basic abundance and feeding data, particularly for key exotic species. The relative P and F calculations allow us at least to define clear alternative hypotheses about possible predation and food impacts, without pretending that we can quantify each of the component calculations required to justify any particular hypothesis.
In the first (1993 baseline) simulation year of each scenario, we calculate the equation A13.3 H, P, and F monthly factors for every indicator species, and then use these to calculate K1 and K2 so that N(1,12) (age 1 recruits) will just balance assumed natural mortalities of older animals, provided that habitat, predation, and food conditions remain constant. K1 is estimated over reaches as a single, nonspatial factor, using observed relative abundances by reach to weight the spatially varying H, P, and F factors. But the K2 "calibration" is done by default on a reach-by-reach basis, so the K2 parameter can represent habitat capacity effects in addition to those modeled explicitly with Hf. This default calculation can be turned off by model users (initialization calculates single abundance-weighted average K2 over reaches), to see if explicitly recognized habitat relationships included in the calculation of Hf can explain observed spatial distribution patterns (this two-stage optional calculation was necessary, particularly in early model development, in order that we could "drive" the submodels for particular species with reasonable spatial relative abundance estimates for predator/competitor species, and work through the habitat linkage parameterization in some systematic way across species).
In fact, K1 represents a "compensation parameter", in the sense that the product Sm(m) over months represents maximum survival rate of eggs to age 1 yr. Model users can either specify this maximum survival rate directly, or can assume the maximum survival rate to be K*(R0/E0), where R0/E0 represents the survival rate needed to produce a population equilibrium at the baseline (1993) egg production rate E0. In the second approach, K* represents the ratio of maximum survival rate at very low population density to the survival rate for a balanced population. There are no empirical data on K* for Grand Canyon vertebrates (no stock-recruitment data); based on comparative studies of fish recruitment relationships (Myers and Barrowman 1996), we have advised users to assume K* values on the order of 3-10.
Each "habitat linkage function" Hr(m) and Hf(m) is calculated as a product of effects over habitat factor values for month m. (Habitat factor values available in the simulation for each reach, and month include temperature, turbidity, max-min stage, wetted area, and warm tributary + backwater area). Using the interface shown in Appendix 8, model users can sketch functions of the form h(Vk), where 0< h <1, and Vk is the value of the kth habitat factor in month m (e.g., V1 is the max-min stage, V5 is turbidity); V scales are set relative to 1993 baseline values. Each H is then just the product h(V1)h(V2)… over those factors V for which the model user has sketched some relationship ( h = 1 for "inactive" V's). By defining H as a product of h(V) effects (rather than, say, a sum of effects), we assume that each habitat factor has a strong effect independent of other factors (a high f value for one habitat variable cannot "compensate" for a low value for another variable, e.g., having a large habitat area cannot compensate for poor thermal conditions). In the same model interface, users can sketch the vm function (0-1 relative values) defining how sensitivity to both H and P/R varies with age over the first year of life; we initially allowed definition of a separate vm function for each habitat factor, but we found this greatly complicated the functional specifications without substantially improving our ability to represent alternative hypotheses about the importance of various habitat factors.
The salt cedar-willow community is of particular concern for future ecosystem management. It is variously described as a preferred nesting and feeding habitat for neotropical birds (Brown and Trossett 1989), a key source of insect production (Stevens 1985), an unnatural eyesore, the only source of shade and wind protection in this harsh, windy desert river system, and an annoyance for campers (very dense stands are virtually impassible). There is no clear consensus about whether this species represents a good or bad change in the ecosystem.
Table 2. Directions of change in major indicator variables predicted by GCM for several water management options. Symbols are as follows: positive impact of a policy (+); negative impact (-); and gross uncertainty (?), i.e., the model prediction can go either way depending on uncertain quantitative parameter values. More extreme changes and uncertainties are shown by multiple signs. Time scale (in years) to complete major transient change is shown in parentheses.
Policy option
Response indicator
Optimize flows for power production
Eliminate diurnal flow variation, allow seasonal changes
Seasonally adjusted steady flowsa
Beach/habitat-
building flowsWarmwater release from GCDb
Warmwater release plus turbidity addition at GCD
Delivered power cost to ratepayers
-- (0)
+ (0)
++ (0)
0/+ (0)
++ (0)
+++ (0)
Sand beach area (campsites and vegetation)
+ (0.5)
-- (1-3)
? (1-3)
++ (0)
+ (1-3)
Main system sand storage
- (5)
+ (5)
-- (3-5)
- (0)
++ (1-3)
Autochthonous primary production
-- (0.1)
+ (0.5)
- (1-2)
+ (0)
-? (1)
--- (0.1)
Riparian plant and insect production
-- (1)
- (5)
-- (2-10)
- (0)
+ (5)
Aquatic insect production
-- (0.5)
+ (1)
-- (2)
- (0)
-? (2)
--- (0.5)
Backwater habitat productivity
? (1-10)
? (10-20)
? (1-20)
(0)
? (1-20)
Trout fishery
- (3)
+ (5)
-- (5)
- (5)
-- (3)
--- (0.5)
Warmwater exotic fishes
-- (5)
?? (5)
?? (5-10)
? (5-10)
?? (10)
?? (10)
Humpback chub
? (15)
? (15)
? (15)
? (15)
? (15)
? (15)
Native suckers (flannelmouth, bluehead)
?? (15-25)
?? (15-25)
?? (15-25)
? (15-25)
?? (15-25)
?? (15-25)
Riparian birds (waterfowl, Peregrine Falcon)
- (5-10)
+ (5)
- (10)
? (10)
-? (10)
--- (10)
Conflicting objectives and trade-offs: uncertain costs and benefits of restoration
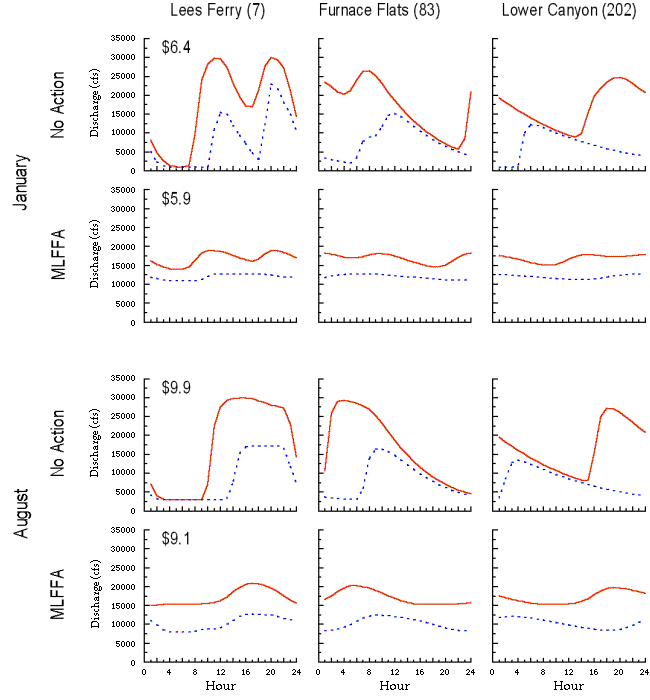
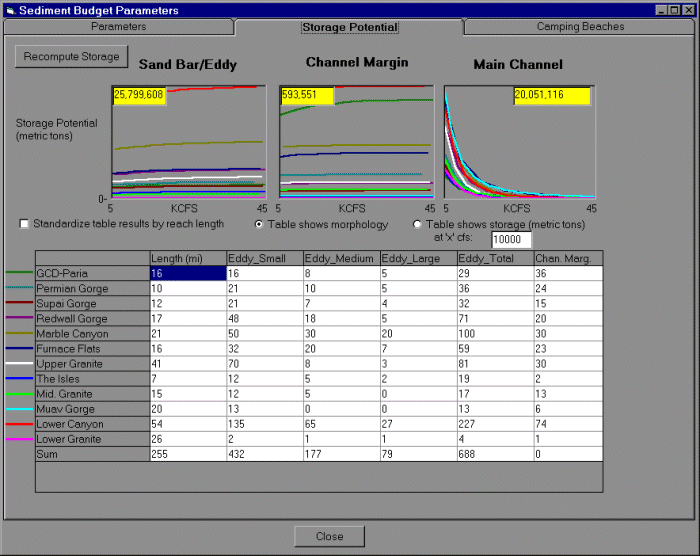

Ci+L = Ceq + (Ci - Ceq) exp{-vWiLi/Qi}
(A4.1)
where
Ceq :
the equilibrium concentration or temperature that would occur if the sample water parcel moved forever over an infinitely long reach at fixed gain and loss rates and no change in cross-sectional area;
Ci - Ceq :
the extent of the departure of the equilibrium concentration or temperature from the upstream boundary condition (Ci); and
exp{-vWiLi/Qi} :
a modifier on the equilibrium departure (a multiplying factor 0-1), which is an exponentially decreasing function positively related to the sinking or heat exchange rate, wetted width, reach length, and inversely related to discharge. For example, the longer the reach, the more closely the downstream boundary concentration or temperature will approach the equilibrium level.
ΔM/Δt = RW - sWC .
(A4.2)

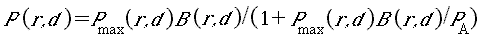
(A6.1)
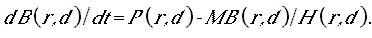
(A6.2)
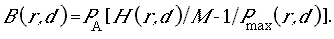
(A6.3)
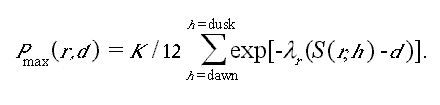
(A6.4)
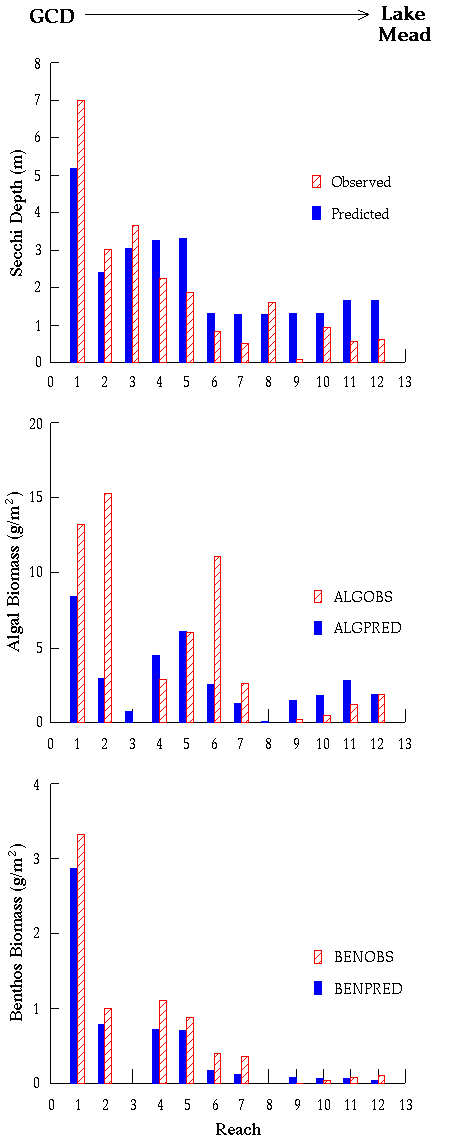
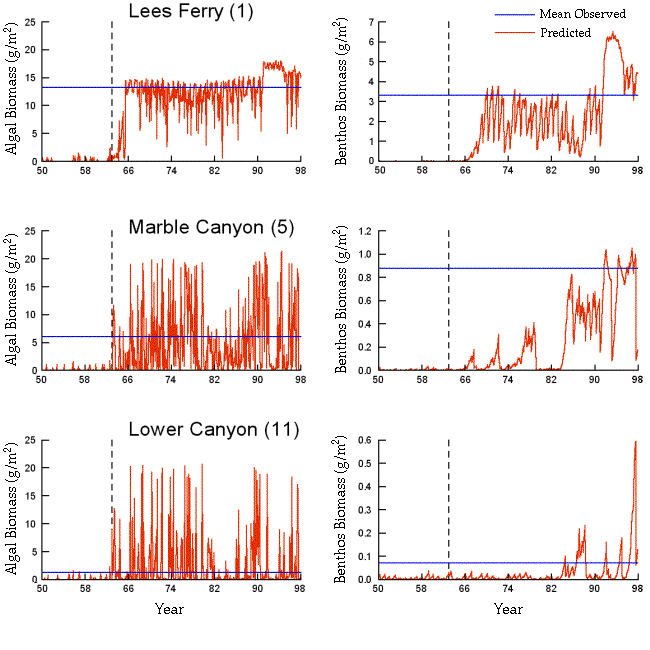
Bsr(m + 1) = Bsr(m)[1 + gsr(Fsr(m)) - msr(m)]
(A9.1)
gsr(Fsr(m)) = efMFsr(m))/[rM + fBsr(m)/V].
(A9.2)
Bprd(t + 1) =
Bprd(t)[1 +
Gprd(t)]Sprd(t)+s.
(A10.1)
Gprd(t) =
rp[1 -Bprd(t)-ΣkakpBkrd (t)].
(A10.2)
Wr(m + 1) =
0.5Wr(m) +
0.5Dr(m).
(A10.3)

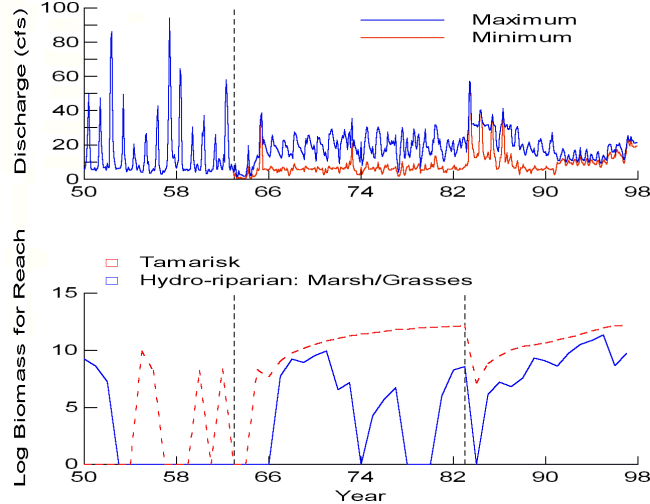
N(t + 1) = SaN(t) + R(t + 1)
(A13.1)
B(t +1 ) = Sa[AN(t)+ρB(t)] + wkR(t + 1)
(A13.2)
N(1,0) = E(t)Segg
Sm(m) = exp[-K1vmHr(m)P(m)/F(m)]
N(1,m + 1) = N(1,m)Sm(m) /(1 + K2 (1 - Sm(m))N(1,m)/ (vmHf(m))]
(A13.3)