|
|
|
Copyright © 2000 by The Resilience Alliance
The following is the established format for referencing this article:
Brook, B. W., M. A. Burgman, and R. Frankham. 2000. Differences and congruencies between PVA packages: the importance of sex ratio for predictions of extinction risk. Conservation Ecology 4(1): 6. [online] URL: http://www.consecol.org/vol4/iss1/art6/
A version of this article in which text, figures, tables, and appendices are separate files may be found by following this link.
Report Differences and Congruencies between PVA Packages: the Importance of Sex Ratio for Predictions of Extinction Risk Barry W. Brook1, Mark A. Burgman2, and Richard Frankham1
1Macquarie University; 2University of Melbourne
- Abstract
- Introduction
- Methods
- Results
- Discussion
- Conclusions and Implications
- Responses to this Article
- Acknowledgments
- Literature Cited
- Appendix 1
Population viability analysis (PVA) is used in conservation biology to predict extinction probabilities for threatened species. Previous studies have revealed large differences between the predictions of PVA modeling packages, but these comparisons included a range of nonstandard factors. A standardized comparison of five PVA packages (GAPPS, INMAT, RAMAS Metapop, RAMAS Stage, and VORTEX) was conducted on six examples (two mammals, two birds, one reptile, and a hypothetical bird/mammal-like life history). The individual-based packages (GAPPS and VORTEX) predicted a consistently higher risk of extinction than their matrix-based counterparts (INMAT and the RAMAS programs). This arose as only the former considered the effect of demographic stochasticity in the sex ratio. The difference was eliminated when only females were modeled in the matrix-based packages. To avoid underestimating extinction risk, only the limiting sex should be modeled in matrix-based PVA packages.
KEY WORDS: demographic stochasticity, extinction risk, individual-based models, matrix-based models, model comparison, parameter estimation, population viability analysis, sex ratio.
Published: March 10, 2000
Population viability analysis (PVA) using computer simulation is now widely applied in conservation biology to assess the impact of current and future threats that endangered species inevitably face. PVA provides quantitative estimates of risk (Burgman et al. 1993) and thus presents a useful and influential planning tool for evaluating research priorities (Clark et al. 1991). By simulating a range of possible scenarios that a species may face in the future, PVAs are often used to compare alternative management and recovery options (Lindenmayer et al. 1993). In some high-profile endangered species, detailed, species-specific PVA models have been developed (e.g., Northern Spotted Owl; Boyce 1994), but these are usually expensive and time consuming. In addition, they are not subject to repeated use, and so could contain undetected flaws. Therefore, conservation biologists frequently turn to commercially available “generic” PVA packages. These offer the most promising prospect for improving PVA, as they are open to scrutiny, evaluation, and iterative development (Brook et al. 1997a).
Various PVA packages are now available, each with differing capabilities. These include the individual-based programs GAPPS (Harris et al. 1986) and VORTEX (Lacy et al. 1995), and the matrix-based (cohort) packages INMAT (Mills and Smouse 1994), RAMAS ® Metapop (Akçakaya 1997), and RAMAS ® Stage (Ferson 1994). All are suitable for population risk assessments, although each was designed with slightly different objectives in mind, reflected in their structure, capabilities, and assumptions (see Possingham et al. 1993, Lindenmayer et al. 1995). These simulation programs provide a convenient tool for building predictive models based on the life history traits, deterministic factors, and stochastic processes that together control the dynamics of natural populations (Shaffer 1981, Gilpin and Soulé 1986).
Different PVA programs have been shown to give divergent predictions in previous comparative studies (Mills et al. 1996, Brook et al. 1999). However, these findings were based on analyses from a single species, and the differences arose because the input was not completely standardized across programs (i.e., the underlying deterministic models were not exactly matched, and nonstandard factors such as inbreeding depression and stochastic breeding structure were included). Although conceptually similar, the models differed in subtle, but consequentially important, ways, which led to incongruent predictions.
However, it remains unclear whether generic PVA packages produce concordant predictions when inputs are strictly comparable and the same characteristics are included. This is an important issue in conservation biology, because wildlife managers often rely on only a single computer package when carrying out viability assessments. Comparisons among packages over a range of taxa should enable us to determine whether PVA packages differ in the magnitude, rank order, and sensitivity for a range of life history strategies. It should also provide means of identifying sources of incongruency, help to detect unstated or hidden assumptions, check the computational reliability of the underlying models (including the detection of software bugs), and establish the importance of subtle differences between PVA packages.
The aims of this study were to determine:
(1) whether there are differences between the predictions of five PVA packages under standardized conditions;
(2) whether differences were obvious in only some output metrics (e.g., extinction probability vs. average population size);
(3) whether particular PVA packages consistently produce higher or lower risk estimates, or whether the pattern of similarities and differences depends largely on the species examined.
Five of the most widely applied generic PVA packages were used in this study: GAPPS, INMAT, RAMAS Metapop, RAMAS Stage, and VORTEX. To compare the implementation of the same model by different packages, a stochastic model was built that was compatible with the design limitations of all of the PVA packages. No nonstandard (optional) input parameters were included (see Table 1 for a list). This model structure was applied to six species. The standardization procedure is described in Appendix 1.
|
Table 1. A list of the standard/common input parameters (upper section) and nonstandard/optional parameters (lower section) included in the five generic PVA packages, GAPPS, INMAT, RAMAS Metapop (R META), RAMAS Stage (R STAGE), and VORTEX.
1
Complete correlation in environmental stochasticity between survival and reproduction.
2 Density dependence.
|
The six examples considered in this study consisted of two mammals (a herbivore and a carnivore), two birds, a reptile, and a hypothetical bird/mammal-like life history with a low growth rate and low levels of environmental stochasticity. The five real-life examples are based on species for which detailed monitoring and ecological data are available. The model parameters are therefore realistic, and represent the type of species modeled in recent PVAs (for reviews, see Burgman et al. 1993, Lindenmayer and Possingham 1994, Lacy et al. 1995). A précis of each species (and the two-letter code henceforth used in the text) are given in Table 2.
|
Table 2. Key biological attributes and references for the six species examined in the standardized PVA comparisons. The species “code” is used in all other tables and figures. N (Ext) is the initial population size when extinctions are measured (all projected for 50 years). N/T (No Ext) is the initial size and simulation duration for those simulations set up to show no extinctions.
1
Vucetich
et al. (1997), Peterson et al. (1998). An isolated population restricted to Isle
Royale, and island in Lake Superior.
2
Lowe
(1969), Clutton-Brock et al. (1982). An island population (west Scotland) declining
due to culling pressure.
3
Mirande
et al. (1997). A long-lived, migratory, endangered North American crane.
4
Tinkle
et al. (1993). A small lizard inhabiting semiarid grasslands of western United States.
5
Brook
et al. (1997)
b.
L.H.I. = Lord Howe Island. A small, ground-dwelling, flightless rail endemic to
the island, east of Australia.
6
Hypothetical
generalized bird or mammal-like life history.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Simulation conditions
Each of the PVA packages (except GAPPS) provides a computation of the deterministic growth rate, based on the input population model. In each case, this was checked to ensure that the underlying deterministic components of the models were identical across all packages. It was found that the deterministic projections of the models (i.e., excluding demographic and environmental stochasticity) were identical in INMAT and the RAMAS programs. It was not possible to run a deterministic projection in GAPPS or VORTEX.
For each example, two sets of stochastic simulations were run with each of the five PVA packages, with either (1) demographic stochasticity only, or (2) both environmental and demographic stochasticity included in the models. It was not possible to run the simulations with only environmental stochasticity applied (i.e., excluding demographic variation) in GAPPS, INMAT, and VORTEX, so this scenario could not be evaluated across packages.
Two separate comparative simulations were run on each taxon. The first was concerned only with measuring the risk of extinction or quasi-extinction. Prior to running the final simulations, test runs were conducted for 50 years, and the initial population size was adjusted to ensure that all packages showed a greater than zero extinction risk under demographic stochasticity only. Equivalent simulations that also included environmental stochasticity resulted in nonzero extinction risks.
The second set of simulations was used to measure the population size and population growth output measures. Test runs were trialed to guarantee that no extinctions would occur. This was done by adjusting the initial population size. Where necessary, the simulation duration was reduced (to avoid reaching very high population sizes, which causes GAPPS to crash). For each species, the simulation duration and initial population size and distribution were identical across all PVA packages.
Absolute extinction risk is not independent of population growth measures such as mean and median population size. Because extinction (zero population size) acts as an absorbing boundary for the simulation replicates, when the extinction probability increases, the mean population size will decrease.
All simulations were replicated 500 times (for justification, see Harris et al. 1987). This was the preset number of iterations in INMAT. For statistical purposes, this provides a sufficiently high degree of replication, as the 95% confidence intervals for extinction risk are only ±4%. (based on the Kolmogorov-Smirnov test statistic; see Sokal and Rohlf 1995).
Data analysesDifferences between means were compared with ANOVAs and pairwise comparisons with t tests (with a Bonferroni correction on the probability threshold for the number of comparisons). Differences among medians were evaluated using Kruskall-Wallis tests (overall) and Mann-Whitney tests (pairwise), and variances were evaluated with F tests. Extinction probabilities were evaluated using contingency chi-square tests (across all packages). Bonferroni-corrected Kolmogorov-Smirnov tests (based on the confidence interval for percentages of the binomial distribution) were used for pairwise comparisons of extinction probabilities. Sokal and Rohlf (1995) provide a detailed description of all these tests. The Bonferroni-corrected significance level for all these tests was set at 5%.
To detect overall trends across taxa, the PVA packages were assigned a rank (from 1 to 5) for each species, with 1 assigned to the package that produced the lowest estimate of extinction risk (or lowest mean final population size), and 5 assigned to the package that provided the highest risk. If all of the PVA packages were to give similar predictions, on average, the ranks would be equal. The nonparametric Kruskall-Wallis and Mann-Whitney rank tests were used to evaluate this. Power analyses showed that, with a sample size of 6, a difference in rank of >1.7 would be required to show a significant difference between packages.
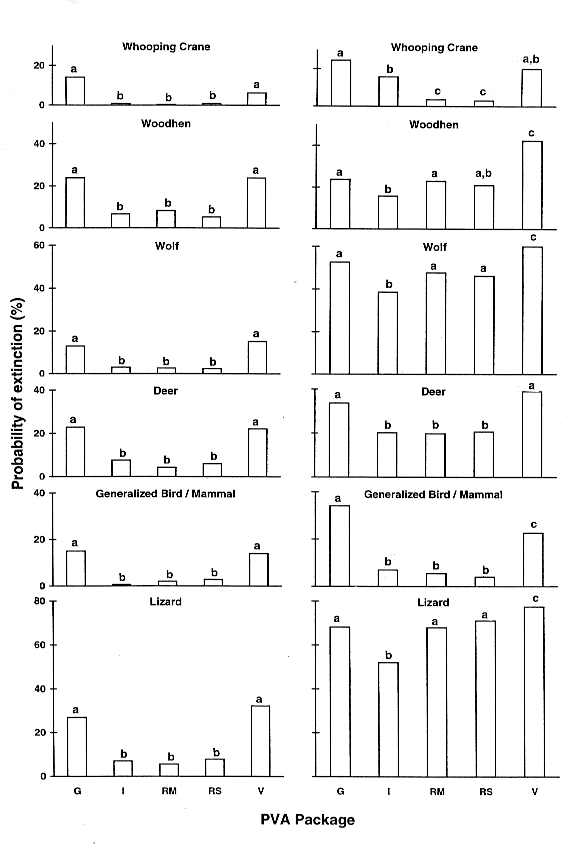
A striking and consistent difference was found between the predictions of the individual-based PVA packages (GAPPS and VORTEX) compared to the matrix-based packages (INMAT, RAMAS Metapop, and RAMAS Stage), with the former group almost always predicting higher extinction probabilities than the latter (see Fig. 1). Under demographic stochasticity alone, chi-square tests revealed a highly significant overall difference between the five packages in all examples (the lowest chi-square [taxa WO] = 118.7, df = 4, P < 0.001). In every case, there was a highly significant difference when GAPPS and VORTEX (individual-based) were compared to any of the matrix-based programs. These differences were not trivial; on average, the individual-based packages predicted an extinction probability 16% higher than did their matrix-based counterparts, ranging from 5% to 24% (depending on the taxon). A 4% difference was significant, based on the Kolmogorov-Smirnov test statistic. There was a significant difference between GAPPS and VORTEX in only one case (WC), and none of the pairwise comparisons revealed a difference between the predictions of INMAT and the two RAMAS packages. A Kruskall-Wallis test showed the rank of these two groups (individual- vs. matrix-based) to be significantly different (H = 21.3, df = 4, P < 0.001; see Table 3).
|
Table 3. The average rank for the five generic PVA packages (I, individual-based; M, matrix-based) for the probability of extinction and the mean final population size (N). Simulations were run under demographic stochasticity alone (D), or with both environmental and demographic stochasticity (ED). Ranks are averaged across the six standardized examples HP, LZ, RD, WC, WH, and WO. A rank of 1 is assigned the lowest risk (or size) and 5 to the highest.
|
When environmental stochasticity was added to the models, the extinction probability increased, but the same underlying trend just described was still obvious. Rank analyses again separated the two groups (H = 19.2, df = 4, P < 0.001), although the average rank of GAPPS decreased and that of VORTEX increased slightly. However, in some examples (e.g., LZ) the differences were masked by the addition of environmental variability. For some packages (especially GAPPS), extinction risk increased less following the addition of environmental stochasticity than it did in others (e.g., the RAMAS family).
Predictions without extinctionBy contrast, no definite difference between the individual- and matrix-based PVA packages was apparent in the projected mean and median final sizes when extinctions were excluded. No package consistently projected the highest or lowest mean size, and the rank order of packages varied depending on the species examined (see Tables 4 and 5). The average ranks (Table 3) showed no significant difference between those under either demographic stochasticity only (H = 0.44, df = 4, P = 0.979), or under both environmental and demographic stochasticity (H = 1.5, df = 4, P = 0.833; Table 3).
|
Table 4. Demographic stochasticity alone: projected mean final size (and standard deviation) with no extinctions, as predicted by the five generic PVA packages for the six standardized examples (see Table 2 for species codes).
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 5. Environmental and demographic stochasticity: projected mean final size (and one standard deviation) with no extinctions, as predicted by the five generic PVA packages for the six standardized examples (see Table 2 for species codes).
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
However, the variability across simulation replicates (represented by the s of the mean final size) were frequently very different (Tables 4 and 5; F tests were significant if the ratio of the squared s (variances) > 1.24). These results are consistent with those for the extinction probabilities, i.e., greater in the individual- than in matrix-based packages. Thus, the two packages that gave the highest extinction risks also gave the most variable population sizes. Under demographic stochasticity alone, there was a significant difference between PVA packages (rank analysis H = 10.3, df = 4, P = 0.035). Paired tests revealed that GAPPS and VORTEX showed a consistently higher variability than INMAT and the two RAMAS programs (e.g., for GAPPS vs. INMAT, Mann-Whitney W = 52.5, df = 6, 6, P = 0.037). When environmental stochasticity was included, the rank analysis again proved significant (H = 9.9, df = 4, P = 0.042), but it was GAPPS that showed lower variability than the other five packages. In this case, VORTEX was not significantly different in rank to the matrix-based programs.
Important and consistent differences were evident between the predictions of extinction probability for the individual-based packages (GAPPS and VORTEX: higher risk) vs. the matrix-based packages (INMAT, RAMAS Metapop, and RAMAS Stage: lower risk) in standardized comparisons. The explanation lies in the implementation of demographic uncertainty in the sex ratio.
In modeling both males and females, the individual-based packages consider the possibility of a temporarily unequal sex ratio. By contrast, the matrix-based programs either ignore differences between the sexes, or, alternatively, model only females. When monogamous breeding is modeled, a temporary shortage of males can greatly decrease the breeding rate and increase the extinction risk (see McCarthy et al. 1994, Brook et al. 1999). However, the standardized models examined in this study were set up under a polygamous breeding structure; thus, this potentially important element of stochasticity was ignored.
In contrast, a sex ratio imbalance is possible in the individual-based packages, as the total number of females available for breeding may temporarily constitute either less or more than 50% of the total population, because of demographic stochasticity in survival or sex ratio at birth. For example, in the matrix models, an adult population size of 20 always equals 20 breeders (an individual’s sex is ignored). Yet, in the individual-based models, an adult population of 20 may temporarily consist of 15 males and 5 females (substantially decreasing the population’s realized reproductive output), or, equally, it may consist of 5 males and 15 females (increasing the reproductive output). Although these fluctuations will cancel out, on average (reflected in the relative congruence of the projected mean sizes), the variability of the population growth rate in the latter case will be greater, especially at small population sizes. It seems highly likely that the greater fluctuations induced by this sex ratio factor are the major reason GAPPS and VORTEX predict higher risks than did INMAT and the RAMAS programs.
Confirmation through simulationThis explanation was tested with RAMAS Stage, which is flexible enough to model either one or both sexes. Using the HP life history and including only demographic stochasticity, RAMAS Stage was set up to model males and females separately (as in GAPPS and VORTEX). As an initial test run, both “males” and “females” were allowed to produce offspring (directly equivalent to the standard matrix model). The predicted extinction risk from this model, 1.6%, was not significantly different from that predicted by the conventional single-sex matrix model of 2.4% (based on the Kolmogorov-Smirnov confidence interval test). The RAMAS Stage model was then altered so that only females produced offspring (with their fecundity doubled), making it essentially equivalent to the two-sex, individual-based models of GAPPS and VORTEX. The mating system remained polygamous, because the number of breeding females was not dependent on the number of available males.
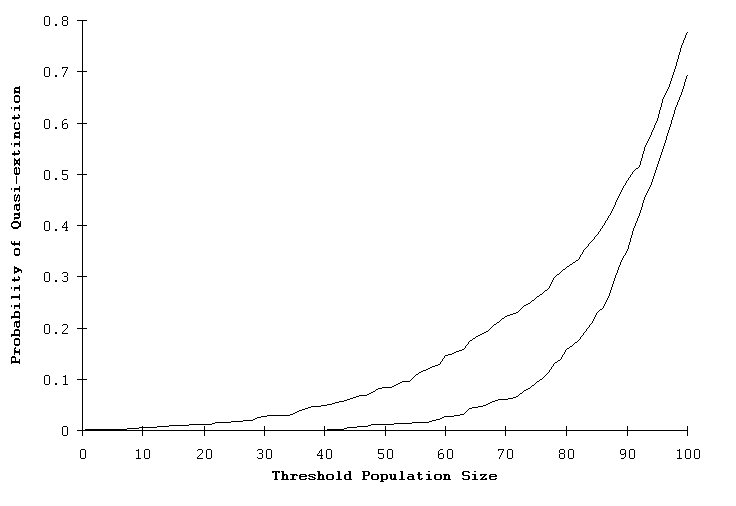
When this RAMAS Stage model was run, the predicted extinction risk increased to 13.1%, not significantly different than that of GAPPS (15.1%) or VORTEX (14.3%). Further, when the two RAMAS Stage models (single- and two-sex models) were run with an initial size of 100, there remained large differences in their predicted risk of quasi-extinction, as illustrated in Fig. 2. The standardized model of the Whooping Crane described by Brook et al. (1999) did not show any clear difference between the individual- and matrix-based PVA packages because the predicted extinction probabilities under demographic stochasticity were close to zero.
Solution: Model only females in matrix-based PVA packages
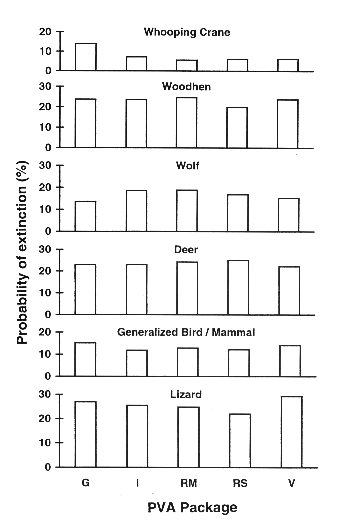
Conventional matrix-based PVA models are likely to underestimate the true extinction risk if both sexes are included. The most straightforward remedy to this problem is to ignore the male component of the population entirely when using matrix-based programs, and to model only females (the limiting sex for breeding). The parameters for vital rates should be those for females only. In rare instances where males are the limiting sex (e.g., Emus; Cayley 1991), they should be modeled instead. To evaluate this solution, we halved the initial population size in the matrix-based packages (e.g., in the WH example, a size of 25 was used in INMAT and RAMAS and 50 in GAPPS and VORTEX) and re-ran the simulations. This resulted in very similar predictions of extinction across all five packages (see Fig. 3). Statistical comparisons were nonsignificant in all cases.
Modeling only the limiting sex in matrix-based PVA packages will produce more appropriate estimates of extinction risk. Although it is pointed out in the RAMAS manuals (Ferson 1994, Akçakaya 1997) that one can either model only the female component of the population, or, alternatively, lump both sexes together, the consequences of the two choices on the predictions of extinction risk (because of demographic stochasticity in the sex ratio) are not specified. In both INMAT and the strictly metapopulation PVA package ALEX (Possingham and Davies 1995), the programs correctly prompt the user to enter females only, but the accompanying documentation does not discuss the implications of this for sex ratio and extinction risk.
Finally, in monogamous species, the number of breeding females depends critically on the number of available males; a stochastic shortage of males will engender a corresponding reduction in the number of females able to breed. Under these circumstances, we advise that a computer package capable of modeling two sexes be applied. In hermaphroditic organisms (such as many plants), the sex ratio issue will not apply.
Congruencies among PVA packagesApart from the differences caused by the sex ratio disparity, the five PVA packages produced encouragingly concordant and consistent output. The underlying population projection models, complex sampling routines, and bookkeeping procedures all worked analogously, despite being implemented in different ways. This overall consistency suggests that the relative rank orders for comparing management options are likely to be similar across different PVA packages.
Recent work testing the predictions of PVA packages (using detailed models covering a range of species) found a high correlation between the predictions of different PVA packages (Brook et al. 2000). This shows that conscientiously parameterized models will produce similar results, irrespective of which PVA package is used. To achieve such an outcome, it is important to take a great deal of care to estimate parameters and to specify variables from data in ways that are consistent with the assumptions of the different packages. The choice of the “best” package for a given problem will depend on the type of available data, the nature of the problems being investigated, and the package’s suitability for the life history of a species, given its available features (see Table 1).
Standardized comparisons revealed a clear and consistent difference between the predictions of the individual-based PVA packages (GAPPS and VORTEX: higher risk) compared to the matrix-based packages (INMAT, RAMAS Metapop, and RAMAS Stage: lower risk). The same trend was evident in all species examined. This difference was because of demographic stochasticity in the sex ratio, a factor modeled in the individual-based packages and ignored in the matrix models. When only females were modeled in the matrix-based PVA packages, the predictions of extinction risk were congruent across all programs. These findings suggest that, to avoid underestimating extinction risk, only the female component of the population should be modeled in matrix-based PVA packages. With this in mind, careful parameter estimation protocols consistent with model assumptions will result in repeatable and transparent models.
Responses to this article are invited. If accepted for publication, your response will be hyperlinked to the article. To submit a comment, follow this link. To read comments already accepted, follow this link.
We thank H. R. Akçakaya, A. Chapman, S. Ferson, R. Lacy, M. McCarthy, J. O’Grady, H. Possingham, and an anonymous reviewer for comments and suggestions. We greatly appreciate the efforts of H. R. Akçakaya and S. Ferson in modifying RAMAS Metapop and RAMAS Stage to provide the raw simulation output, L. S. Mills for providing access to
INMAT’s source code, and R. Harris and R. Lacy for explanations of idiosyncrasies of GAPPS and VORTEX, respectively. This work was supported by ARC and Macquarie University research grants. Publication Number 288 of the Key Centre for Biodiversity and Bioresources, Macquarie University.
The procedure used to standardize the input model across the five PVA packages.