|
|
|
Copyright ©1999 by The Resilience Alliance*
The following is the established format for referencing this article:
Carpenter, S., W. Brock, and P. Hanson. 1999. Ecological and social dynamics in simple models of ecosystem management. Conservation Ecology 3(2): 4. [online] URL: http://www.consecol.org/vol3/iss2/art4/
A version of this article in which text, figures, tables, and appendices are separate files may be found by following this link.
Research, part of Special Feature on Recent Advances in Ecological Theory and Practice Ecological and Social Dynamics in Simple Models of Ecosystem Management Stephen Carpenter, William Brock, and Paul Hanson
University of Wisconsin
- Abstract
- Introduction
- The Environmental Problem: Lake Eutrophication by Nonpoint Pollution
- Cost-benefit Optimization
- Market Manager Model
- Governing Board Model
- Land Manager Model
- Discussion
- Note about Computer Programs
- Responses to this Article
- Acknowledgments
- Literature Cited
Simulation models were developed to explore and illustrate dynamics of socioecological systems. The ecosystem is a lake subject to phosphorus pollution. Phosphorus flows from agriculture to upland soils, to surface waters, where it cycles between water and sediments. The ecosystem is multistable, and moves among domains of attraction depending on the history of pollutant inputs. The alternative states yield different economic benefits. Agents form expectations about ecosystem dynamics, markets, and/or the actions of managers, and choose levels of pollutant inputs accordingly. Agents have heterogeneous beliefs and/or access to information. Their aggregate behavior determines the total rate of pollutant input. As the ecosystem changes, agents update their beliefs and expectations about the world they co-create, and modify their actions accordingly. For a wide range of scenarios, we observe irregular oscillations among ecosystem states and patterns of agent behavior. These oscillations resemble some features of the adaptive cycle of panarchy theory.
KEY WORDS: adaptive agent models, adaptive management, bounded rationality, ecological economics, ecosystem oscillations, integrated models, lake eutrophication, nonpoint pollution, phosphorus cycles, simulation models, social-natural systems.
Published August 6, 1999.
Ecosystem management is changing rapidly. Command-and-control programs that neglect intrinsic cycles of natural and social systems appear to be insufficient, or even worse than doing nothing (Holling and Meffe 1996). Instead, approaches that involve diverse participants in assessment, learning, and planning may lead to more flexible, adaptive institutions and sustainable outcomes (Lee 1993, Gunderson et al. 1995). "Citizen science" (Lee 1993) aims to engage stakeholders, scientists, and managers in an ongoing dialogue about the kinds of ecosystems people want and the kinds of ecosystems people can get. Little is known, however, about the fluctuations of social and natural systems that might be created by citizen science in its various forms. The dynamics of diverse human agents interacting with ecosystems fall between several traditional academic disciplines. Although case studies of such interactions exist, models are few and theories are rare. A promising theory is the panarchy of adaptive cycles, which posits perpetual and ever-changing oscillations between periods of exploitation, crisis, learning, and renewal (Gunderson et al. 1995). Models that can bridge this theory to experience in specific, testable ways are lacking.
Computer models play diverse roles in ecosystem management. They are used to design engineering structures, forecast ecosystem changes, estimate statistical parameters, summarize detailed mechanistic knowledge, and have many other applications. Such models are designed to perform well on certain narrowly defined tasks (e.g., to yield unbiased predictions with specified uncertainties for a particular process). Computer models can also be used as caricatures of reality that spark imagination, focus discussion, clarify communication, and contribute to collective understanding of problems and potential solutions (Holling and Chambers 1973, Holling 1978, Scheffer and Beets 1994, Walters 1994, Janssen 1998). The role of such models is similar to the role of metaphor in narrative. The models are designed to illustrate general patterns of system behavior, rather than to make specific predictions. They should be usable and understandable by diverse participants, and easily modified to accomodate unforeseen situations and new ideas. This paper presents models of the metaphorical type.
Many case histories of ecosystem management are available (e.g., Holling 1978, Lee 1993, Gunderson et al. 1995, Walters 1997). These cases have several common features that suggest the minimal elements of models that are sufficient representations of ecosystem management. These are:
1) Ecosystem dynamics that involve nonlinear interactions of variables with distinctly different turnover rates (Carpenter and Leavitt 1991, Levin 1992, Gunderson et al. 1995, Carpenter and Cottingham 1997, Ludwig et al. 1997). Resource exploitation and research often focus on relatively fast variables. Long-term changes, resource collapses, surprises, and new opportunities often derive from relatively slow variables.
2) A social arena in which agents assess the status and potential future state of the ecosystem, compare possible actions, and choose policies (either individually or collectively) that subsequently affect the ecosystem and the scope of future choices. An enormous variety of such systems can be envisioned. We present examples selected for their simplicity and diversity. Even these minimal representations yield complex dynamics that mimic patterns known from many case studies. Although simple, these models may provide ideas leading toward more realistic and detailed simulations of specific management systems.
The purpose of this paper is to describe three minimal models for ecosystems interacting with people who must act based on inferences about an evolving world that they co-create. Each model is an oversimplification, but the models' strengths and weaknesses may be complementary. Thus, in concert, they may reveal important general patterns. Our goal is to provide contrasting examples of useful minimal models, which include building blocks that could be used to develop more detailed models tailored to other specific situations. We also point out some important questions for future research.
Eutrophication, the over-enrichment of lakes, is the most widespread water quality problem in the United States (NRC 1992) and many other nations. Eutrophication causes explosive growths of noxious, toxic algae and episodes of oxygen depletion that kill fishes and other animals (Smith 1998). Thus, eutrophication causes the loss of some of the potential benefits of fresh water, including consumption by people, irrigation, industrial uses, and recreation. Once a lake is eutrophic, it can be very difficult to reduce phosphorus levels and restore clean water (NRC 1992). Although eutrophication can be reversed in some lakes by simply reducing phosphorus inputs, restoration is not so simple in other lakes (NRC 1992). Some lakes are hysteretic, i.e., their phosphorus inputs must be reduced to extremely low levels for an extended period of time in order to end eutrophication (Carpenter et al. 1999). Pollution in other lakes is irreversible through phosphorus inputs alone; additional interventions are needed to restore such lakes (Carpenter et al. 1999). A model consistent with known dynamics of phosphorus in lake water was analyzed by Carpenter et al. (1999). An expansion of this model to include sediment phosphorus dynamics is used in this paper (Appendix 1). The overfertilization that triggers eutrophication is caused by excessive emissions of nutrients, especially phosphorus, into lakes and rivers. Nonpoint or diffuse sources of phosphorus include runoff from farm fields, urban areas, and construction sites. Nonpoint phosphorus pollution is the major cause of eutrophication in the United States (Carpenter et al. 1998). In the United States and Western Europe, phosphorus is accumulating in agricultural soils (NRC 1993, Carpenter et al. 1998). This accumulation is associated with high densities of livestock and overfertilization of crops using phosphorus obtained by mining ancient sedimentary deposits (Bennett et al. 1999). Soil erosion subsequently transports the phosphorus to rivers and lakes, where it causes eutrophication. Intensification of agriculture in the developing world is likely to expand the global scope of eutrophication, with potentially severe implications for water supplies. Nonpoint pollution has proven to be a stubborn environmental problem. Soil phosphorus dynamics are slow compared to those of aquatic ecosystems (Bennett et al. 1999). Only a small fraction of the phosphorus stored in upland soils is sufficient to cause severe eutrophication of the freshwaters of a catchment (Bennett et al. 1999). Management practices to control nonpoint phosphorus pollution can be expensive (NRC 1993, Novotny and Olem 1994). Implementation requires changes in farmer behavior or interventions by government in the management of private lands. Economic pressures to increase livestock herd sizes and fertilize more intensively lead to increased mobilization of phosphorus in agro-ecosystems. Thus, many factors interact to exacerbate nonpoint pollution and create obstacles to mitigation of eutrophication. The models presented here represent the key ecological processes and some simple models of the social interactions involved in the management of lakes subject to nonpoint phosphorus pollution.
Many studies have used cost-benefit analysis (CBA) to assess the trade-offs between the benefits derived from polluting activity and the environmental losses that derive from pollution (Dixon et al. 1994). In the case of lake eutrophication, the benefits from polluting activity include profits from farming and development. The losses include foregone uses of the lake or its water for human consumption, irrigation, industry, or recreation (Wilson and Carpenter 1999). Optimization methods are used to calculate the policy that maximizes the net benefits from polluting activity and ecosystem services (Appendix 3).
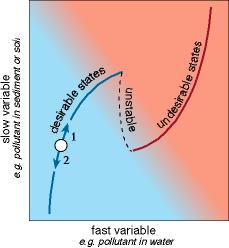
A schematic summary of optimization of a multistable ecosystem (Fig. 1) shows that economic criteria can either move the system toward a breakpoint where it may collapse to an undesirable state (arrow 1), or away from the breakpoint (arrow 2; Carpenter et al. 1999). Along arrow 2, the resilience (domain of attraction of the desirable steady state) is growing. Along arrow 1, resilience is declining. Thus, economic optimization can act to either increase or decrease resilience. Note that Fig. 1 represents only two dynamic variables, a slow one and a fast one. It would be more realistic to include nested processes with several different turnover rates spanning several orders of magnitude (Levin 1992). In such a situation, the curves of Fig. 1 would change over time according to the dynamics of the slower variables. Thus, resilience could grow or shrink due to dynamics that are inapparent from a static two-dimensional analysis.
Cost-benefit analysis shows that the optimal level of phosphorus in a lake is quite sensitive to stochasticity in the inputs (e.g., effects of climate), variance in the ecological parameters of the model used to forecast lake dynamics, and variance in the economic values attached to the various benefits and costs (Carpenter et al. 1999). Even in situations in which decades of high-quality data are available, uncertainties dominate the analysis (Carpenter et al. 1999). Hence, the conclusions of CBA are likely to be challenged by those who are most affected by the outcome. Because any important CBA is likely to be controversial, the arena in which actual decisions are made will be larger and more complex than the ecological and economic information used in the CBA. Thus, it is important to consider the impacts of CBA in a broad ecological and social context.
The ecological and social models used to estimate the parameters for CBA are necessarily simplifications. On the ecological side, these models usually omit slow variables and nonlinearities, because these are very expensive (perhaps sometimes impossible) to quantify. The models often fail to represent the evolved and evolving nature of ecosystem components, which may be sources of resilience or surprise. Therefore, the analysis always omits potentially important outcomes, simply because they have not yet been observed or cannot be forecast. Also, the cost-benefit analysis is maximizing expected utility in a statistical sense (Lindley 1985). In other words, the optimal decision is a gamble, not a sure thing. Any single realization of the policy could have negative and long-lasting consequences. For this reason, CBA is certain to cause errors in policy choice, although these errors may be infrequent. When the errors occur, ecosystem surprises will impact stakeholders differently and may have dramatic effects on social organization and subsequent policy choice. Interest in such dynamics is a motivation for the models that follow.
Information market models represent dynamics of choices by agents having heterogeneous beliefs and expectations. We assume a large number of agents, and that no agent, or collection of agents, can manipulate the overall outcome. We assume that the aggregated influence of agents' expectations on social and ecological dynamics is significant. However, there is no possibility for all agents, or some significant fraction of the agents, to manipulate the total system (ecological system plus socioeconomic system) to both learn its true dynamics and control its stability. At each time step, each agent is assumed to assess the information available to him or her, and to choose a level of pollutant input to the ecosystem. Total inputs are the sum of agent choices. Learning and preferences are updated regularly as new information becomes available.
Behavior of this sort of model was reviewed by Grandmont (1998). He concludes that such systems are likely to be unstable under conditions of interest to us. Instability is generated by the agents' uncertainty about system dynamics, which causes them to extrapolate a wide range of apparent regularities derived from past fluctuations of the system. Some of these apparent regularities lead to divergence of system dynamics. The models are stable only under fairly restricted conditions: (1) expectations have little impact on the system, so that learning has little impact; or (2) agents extrapolate from only a narrow range of the apparent trends. The former situation implies an uncoupling of social and ecological systems, which is outside the scope of this paper. The latter situation implies sophisticated knowledge of local stability conditions, as might arise if slow ecological drivers were stationary. Such a situation is irrelevant to sustainable management of ecosystems. Therefore, the market models of interest to us may be unstable, exhibiting cyclic or chaotic dynamics with a diversity of possible attractors, depending on parameter values and initial conditions.
Fig. 2 illustrates a single iteration of a Market Manager model. Each time step begins with updating the state of the lake, based on the agents' most recent choices of pollutant input (Appendix 1). The Monitoring, Assessment, and Forecasting component (MAF) receives data (with observation error) on the state of the lake and estimates parameters of a forecasting model for future pollutant levels in the lake water (Appendix 2). The MAF makes a subset of the information freely available to the agents. This free information consists of a running average of pollutant levels (Appendix 1) and values of a reversibility parameter that can be used to forecast future pollutant levels as a function of input choices (Appendix 2). In the simulations presented here, the running average is calculated over time steps t-1 to t-10. The remainder of the information is available at a cost. The costly information consists of the latest data (time t) for pollutant levels and the forecasting model. This is analogous to a situation in which cutting-edge technology is costly, whereas outdated technology is cheap. An independent component of the model provides the agents with information on the recent economic performance of individuals who purchased, or did not purchase, the additional information. This is analogous to a situation in which past market performance is known to individuals who are contemplating a choice among alternative investments (Brock and Hommes 1997).
|
Fig. 2. Market manager model: flow chart of the major interactions. 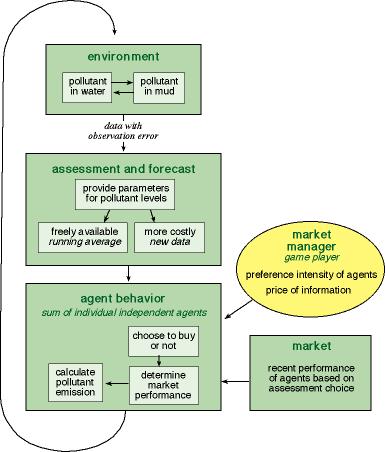
|
At this point, the Market Manager sets the price of information and the preference intensity of the agents. The preference intensity controls how strongly the agents prefer the choice that has been most profitable in the recent past. In the program we have provided, the Market Manager is the person who is playing the computer game. It is also possible to program the model with fixed parameters for the price of information and the preference intensity. Alternatively, an automated learning algorithm, such as a genetic algorithm, could be used to set the price of information and the preference intensity.
Agents choose whether to use the free information or purchase the sophisticated information (Appendix 4) according to a model by Brock and Hommes (1997). They then calculate a pollutant input that maximizes their expected economic return over infinite time, using the available information about the state of the system and the parameters of the forecasting model (Appendix 3). The total pollutant input is the sum of the agent choices, multiplied by a stochastic disturbance factor. We iterate to the next time step. Notice that, at each date t, the expected economic return over t to infinity is maximized, assuming that the parameters are set at their date t estimated values for all future dates. That is, the optimization over date t to infinity does not take into account the impact of future updatings of the parameters, unlike Easley and Kiefer (1988), for example. It is beyond the scope of this preliminary report to conduct a more sophisticated updating scheme.
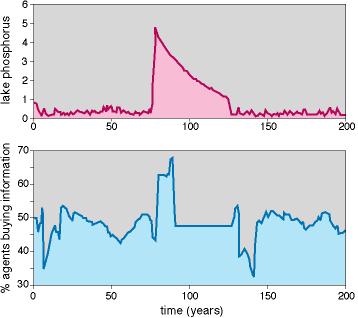
A typical time course from the market manager model shows occasional outbreaks of very high phosphorus (Fig. 3). Slow accumulation of phosphorus in the sediment sets the stage for the outbreaks. The proximal trigger of an outbreak is a large input event (due to the stochastic disturbances of the inputs). Generally, the percentage of agents buying the sophisticated information is declining just before an outbreak. Immediately after the outbreak, there is a period of intensive buying of information, as agents adjust their behavior to the new regime.
Extensive experimentation with the cost of information and the preference intensity parameter suggests that manipulation of the market cannot prevent the outbreaks, although these parameters can appear to change the frequency of outbreaks. The ecosystem and the agents inevitably go through cycles similar to those of Fig. 3. Sediment buildup is inexorable, episodes of low learning (few buyers of sophisticated information), and occasional large input events are inevitable, so outbreaks followed by periods of learning and adjustment occur from time to time.
The Governing Board is composed of a population of competing agents. The agents represent distinctly different attitudes toward the ecosystem. The agents interact to determine policy for pollutant inputs to the lake. Periodically, the agents stand for election. Agents who support policies that appear to have sustained the ecosystem and economic yields are more likely to be elected. Thus, agent composition changes through the election process. This approach contrasts with that of Janssen (1998), in which agents' perspectives evolve through a learning process. In the simulations reported here, the agent perspectives are "environmentalists" who prefer a lower input rate of phosphorus than the "individualists." Differences between environmentalist and individualist perspectives could be caricatured in a number of ways, for example, through contrasting discount factors or beliefs about the reversibility of eutrophication (Heal 1997, Carpenter et al. 1999, Janssen and Carpenter 1999). In the version of the model presented here, the environmentalist policy is calculated using a discount factor of 0.9999, and the individualists always favor a slightly higher phosphorus input rate than the environmentalists.
Fig. 4 illustrates a single iteration of the model. Each time step begins with updating the state of the lake based on the agents' most recent choices of pollutant input (Appendix 1). The state of the lake and the current level of polluting activity determine the overall economic performance, as described by Carpenter et al. (1999). Periodically, a new Board is elected based on apparent performance of environmentalist and individualist policies in the recent past (Appendix 5). The Monitoring, Assessment, and Forecasting component (MAF) receives data (with observation error) on the state of the lake and estimates parameters of a forecasting model for future pollutant levels in the lake water (Appendix 2). This information is used to calculate the individualist and environmentalist policies. The Governing Board then decides the target level of pollutant. The decision-making process can involve compromise, in which the pollutant target results from a balance of perspectives, or a "winner-take-all" system in which the majority group determines the target (Appendix 6). The pollutant input is subject to a stochastic disturbance. At this point, we begin a new iteration.
|
Fig. 4. Governing board model: flow chart of the major interactions. 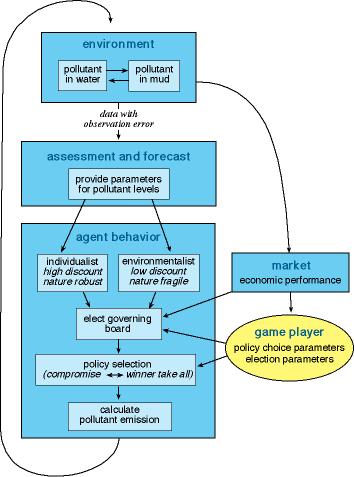
|
In the program we have provided, the player is the Board Director who sets the parameters for the election process (w and φ; Appendix 5) and the decision- making process (iota; Appendix 6). In other versions of the program, the model is run with fixed values of these parameters, or with a learning algorithm that adjusts the parameters to meet some goal.
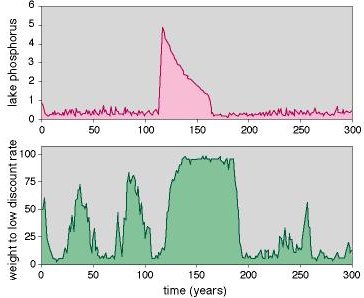
ResultsThe governing board model, like the market manager model, shows occasional outbreaks of very high phosphorus (Fig. 5). Slow accumulation of phosphorus in the sediment sets the stage by moving the lake closer to a breakpoint. The trigger is a large input event. Generally, the proportion of individualists is high prior to an outbreak. Thus, the proportion of environmentalists is low. Following the outbreak, the proportion of environmentalists is high for an extended period. The environmentalist policy appears to perform better while the lake is highly polluted.
As in the market manager model, experimentation with the social parameters (the election process and the decision process) cannot prevent the outbreaks. It is possible to manipulate the frequency and duration of outbreaks through the election and decision parameters, but the outbreaks cannot be eliminated. The ecosystem and the agents inevitably go through cycles similar to those of Fig. 5. Sediment accumulates, the governing board makeup oscillates, and eventually a period of heavy discounting overlaps with a large input event. Outbreaks, followed by periods of stringent management to restore low pollutant levels, are inevitable.
In presentations of these models (and other, similar models not included in this paper), the governing board model has provoked the most discussion and controversy. The representation of the election and decision-making process sometimes evokes emotional responses (both favorable and unfavorable) from participants. This suggests that explorations of alternative representations of these processes would be fruitful. Another feature of this model that stimulates argument is the model used by the MAF component (the "scientists"). Should the MAF component estimate the parameters for the true structural model of the ecosystem, or an approximation (as used here)? If an approximation, which one? Should the MAF component be able to "learn" the structural model through experimentation, as in the models of Janssen (1998)? Finally, one could debate the caricatures adopted for the "environmentalist" and "individualist" perspectives. How should these interest groups' preferred input rates be calculated? The exploration of these issues is left for further research.
In the Land Manager model, a decision maker sets a target pollutant level for the lake. This target affects policies toward phosphorus-intensive and phosphorus-conservative practices on farms. Farmers choose their phosphorus management practices based on policies and the market. Pollutant inputs to the soil and the lake depend on the sum of farmer choices.
The ecosystem differs from that of the previous models (Appendix 1). Soil phosphorus is represented explicitly as a dynamic variable (Appendix 7). Inputs to the lake depend on both soil phosphorus and farmer behavior.
A single iteration of the model (Fig. 6) begins with updating the ecosystem's dynamic variables (Appendices 1 and 7). Ecosystem condition is measured (with observation error) and forecast by a Monitoring, Assessment, and Forecasting component of the model (Appendix 2). The Decision Maker receives this information, as well as information on the overall economic performance (which depends on pollutant emissions and water quality in the ecosystem). In the version of the model we have provided, the decision maker is the person running the computer. It is possible to program the model with a fixed decision rule, or a learning algorithm that adjusts the decision rules to meet some goal.
|
Fig. 6. Land manager model: flow chart of the major interactions. 
|
The decision maker sets a target pollutant level, which determines regulations of phosphorus-intensive farms and incentives to phosphorus-conservative farms. Farmers use a forecasting algorithm (Appendix 2) to anticipate future regulations or incentives. Each farmer decides independently whether to use P-intensive or P-conservative practices, based on expectations of future actions by the decision maker, current regulations and incentives, and the market for farm products (which is external to the model). Farmers' decisions are computed using a Brock-Hommes (1997) market model (Appendix 4). Pollutant inputs to the soil and lake water are the cumulative result of all the farmers' decisions.
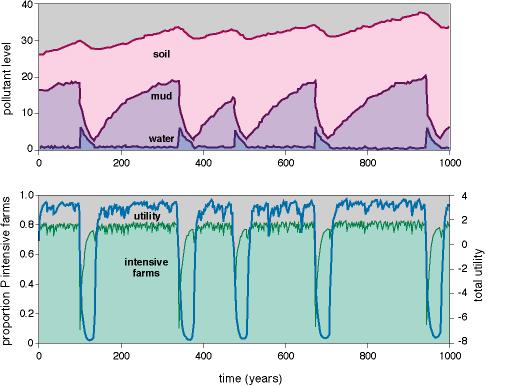
ResultsA series of cycles from the Land Manager model shows slow growth of soil phosphorus (with some oscillation), cycles in mud phosphorus with periods of about 200 years, and occasional outbreaks of high phosphorus in the water (Fig. 7). The proportion of phosphorus-intensive farms is high when water phosphorus is low, but decreases to very few phosphorus-intensive farms when water is highly polluted. The outbreaks of high phosphorus in the water are followed by extreme declines in total economic performance. Economic performance recovers gradually as the lake water phosphorus level declines, and finally returns to relatively high levels when the lake flips to the low-phosphorus steady state and farmers switch back to phosphorus-intensive practices.
A key difference between the land manager model and previous models is that the resilience of the lake can be manipulated by managing the slowest variable, soil phosphorus. Thus, the game player has a mechanism for manipulating the stability of the ecosystem through the slow variable.
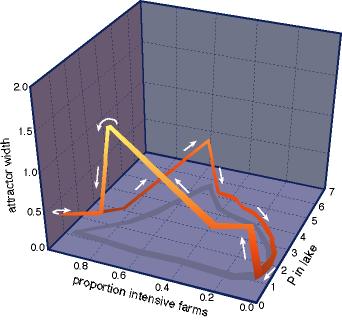
Typical dynamics through a single cycle of the model output illustrate the changes in resilience (Fig. 8). Resilience is estimated as the width of the desirable attractor (in units of water phosphorus) in a phase space of mud phosphorus vs. water phosphorus (Appendix 8). The system spends a long time on the left side of the diagram, with moderate attractor width, high proportion of phosphorus-intensive farms, and relatively low phosphorus levels in the lake. As phosphorus levels rapidly increase, the proportion of phosphorus-intensive farms decreases, but this cannot stop the rapid buildup of phosphorus in the water (which is driven by recycling from the mud). Attractor width quickly drops to zero. Then there is a period with few phosphorus-intensive farms, and a gradual decline in lake phosphorus levels. Eventually the attractor size jumps to a positive value. The desirable attractor has opened up, and the ecosystem falls in. Now the number of phosphorus-intensive farms can be increased. This diminishes the size of the attractor, but not so far that there is an immediate outbreak of phosphorus in the lake. The stage is set for another phase of phosphorus buildup in the sediments and upland soil.
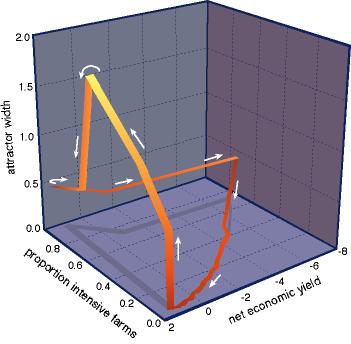
The same cycle can also be depicted using net economic yield as an axis, in place of lake water phosphorus (Fig. 9). The economic collapse is followed by a period of rebuilding. Eventually, the desirable attractor for the ecosystem is re-opened, and economic yield can be further increased by adding phosphorus-intensive farms. This sets in motion the processes that will create the next collapse.
The game player who wishes to sustain the resilience of the system learns that the proportion of phosphorus-intensive farms must be low enough to balance soil phosphorus at a moderate level. This provides more flexibility in manipulating the mud-water system to prevent outbreaks. If soil phosphorus and the number of phosphorus-intensive farms are moderate, then the chance of a large input event that pushes the lake out of the desirable attractor is reduced.
In order to caution the reader against the generality of these findings, and to encourage readers to experiment with their own modifications to these models, it is worthwhile at this point to inquire into what modifications of the current setup might stabilize the intermittent outbreaks of instability. The reader interested exploring a diversity of agent-based models will find a sampling in Sargent (1993), who considers a range of possibilities from rational expectations to adaptive learning.
To make some plausible conjectures about behavior of modifications to the current setup, let us build some intuition into the nature of optimal solutions to the problem of maximization of expected discounted economic returns from management under the model of Appendix 1. For the "true" value of the parameter vector of Appendix 1, assume that there is a unique steady state that maximizes utility over the set of steady states that solve the deterministic model (with ς set equal to zero). Call this steady state the "Golden Rule."
If there is only one type of agent that discounts the future very slightly, then, for general concave utility functions, the work of Brock (1977) may be adapted to show that, in the deterministic case of dynamics like Appendix 1, except for "hairline" cases, the system will converge to a steady state close to the Golden Rule. For the general stochastic case, the work of Marimon (1989) can be adapted to reach a similar conclusion. Call this steady state the Near Golden Rule (NGR). Since, for our case, utility is linear in loading, the optimal dynamics will move the system to the NGR as quickly as possible (Appendix 3).
Suppose that there are infrequent shocks to the P input. The system will be infrequently knocked away from the NGR, but the optimizer will "aim" it toward the NGR and it will be moving there as quickly as possible, subject to constraints (e.g., P inputs must be nonnegative).
Now let the parameters of Appendix 1 be estimated instead of known. We optimize over the infinite horizon and we set the parameter vector at the current estimated value. The optimal dynamics moves the P-level as rapidly as possible to the new NGR, which depends upon the current estimated value of the parameter vector. If the estimated parameter vector changes in such a way that the NGR makes an abrupt change, then the choice of P inputs and the optimal dynamics will make an abrupt change as the system is redirected toward the new NGR. Such an abrupt change can occur due to the presence of a two-humped objective function where the relative height of the humps switches (Ludwig 1998).
It is important to realize that, in a system with one type of actor who discounts the future very slightly, this actor will try to "insure" a valuable future by controlling P inputs, in an attempt to keep the sediment level M down so that the recycling from sediments does not flip the lake into a high P steady state, if the optimal value conditional on being trapped in such a region is lower than the NGR steady-state utility. Low P inputs are more likely if the actor accounts for sources of variance such as stochastic inputs, parameter uncertainties, or lags in implementing policy (Carpenter et al. 1999). This approach can be made even more sophisticated by taking into account the parameter updating, as in Easley and Kiefer (1988).
Notice that if the noise in the P input contains disturbances that are large enough to shift the lake to the high-P state, then we have to wait for the pulse in sediment phosphorus to fall to the level at which the lake can be restored. This possibility could lead to what looks like oscillations (with irregular periodicity), even if there is only slight discounting of the future. This mechanism may be able to produce oscillations in P and in M that look much the bursts in Figs. 3 and 5 and the movements in P and M displayed in Fig. 7. Here's how. Let z(t) in Eq. A1.1 take a very large value by chance. This moves P(t+1) to a very large value (because l(t) is positive). But in the next period, M(t+2) is bumped up to a very large value via Eq. A1.2. Now rM(t+2) is large and the lake is at a high-P steady state even when l(t+3) is set to zero in Eq. A1.1. The single optimizer who barely discounts the future will shut l(.) down to zero until the M level falls, so the P level returns to a low steady state. Even as M continues to fall, this long-view optimizer may hold l(.) down to zero. As soon as the lake gets closer to the long-run optimizer's desired target levels of P, then positive inputs will again be allowed. Positive inputs will be allowed until another very large disturbance occurs. Because tails of a lognormal distribution are thin, such very large events will be rare, but they are sure to happen eventually. Therefore, we will get P pulses that are crushed, as in Figs. 3, 5, and 7. The shape of the pulses and the pattern of their crushing may vary, but at a very rough level of qualitative comparison, the pattern may be similar to that shown here. We suggest that readers try this experiment for themselves.
Estimation of a mistaken model, or uncertainty about the structure of the model that one should estimate, is another important factor in the dynamics. If the agent's knowledge of the true model structure for the ecosystem is incorrect, and the parameters are estimated, diverse outcomes are possible. In environmental assessment, as in other sciences, it is often the case that several alternative structural models are supported by the data (Walters 1986, Brock and Durlauf 1999). What are the consequences if an agent assumes a particular model structure, and then estimates parameters for that model and calculates optimal policies, but the model is incorrect? By experimenting with the Governing Board model, the reader can see that estimates of b (the irreversibility parameter, Appendix 2) can become too optimistic when P levels have been low for a long time. Optimistic estimates of b can lead to overly large inputs of P, because the agent is too optimistic about the capacity of the lake to process P inputs (Carpenter et al. 1999).
The opposite effect can also occur. An agent who believes that the dynamics are linear, when the true dynamics are nonlinear, can underestimate the biodegradation parameter. This, in turn, leads to conservative P inputs and conservative target levels of P relative to the true parameter.
Suppose we ignore the slow variable in Appendix 1, assume that the agent knows that E{N(t+1)} = 1, and write
|
P(t+1) = P(t) + l(t) N(t+1) - b P(t) + r f(P(t)) |
(1) |
but the agent mistakenly believes Eq. 1 is linear
|
P(t+1) = P(t) + l(t) N(t+1) - B P(t). |
(1') |
The agent sees data on P and l up to date T, and estimates B by assuming that E{N(t+1)} = 1 and minimizing
|
E{[Pest(t+1) - P(t+1)]2} |
(2) |
where E denotes time average from t =1,2,...,T and Pest is the forecast of P(t+1):
|
Pest(t+1) = P(t) + l(t) - B P(t). |
(3) |
The actual P(t+1) is generated by the true model (Eq. 1). Estimating B in this fashion, letting Z(t) = P(t+1) - P(t) - l(t) yields
|
Best = -E{Z(t) P(t)} / E{P(t)2} |
(4) |
which converges, as the number of observations increases, to
|
Best = b - r E{f(P) P} / E(P2)} < b for r > 0 |
(4') |
where E{.} denotes limiting time average (if this exists). Eq. 4 was obtained with the assumption E{N(t+1)} = 1 and using iterated expectations.
Equation 4 contains a key message: A mistaken linearist in the nonlinear world (Eq. 1) will end up with a limit estimate Best, which is less than b! This linearist will believe that the lake processes P at a slower rate than it actually does. The mistaken linearist averages over time when the lake processes P slowly (due to the presence of recycling), and because a linear model is used, the agent underestimates the true value of the reversibility parameter b. Because b is underestimated, the linearist may, depending upon the strength of the bias (Eq. 4), choose a lower target level of P and a lower target input rate, relative to the optimum for the true process (Eq. 1). This is the opposite of the outcome seen in the Governing Board model.
What if the agent estimates both b and r (Ludwig 1998)? What if the agent also builds a model for the sediment phosphorus, M? What if the agent has the correct structural model for P and M, but fails to account for slow dynamics of the soil phosphorus in the uplands (Appendix 7)? The role of structural uncertainty in the model that agents assume for the ecosystem they manage is likely to be crucial to the dynamics. At this point, most of the interesting questions are unresolved.
Even a manager with perfect knowledge and perfect control of the social system can create outbreaks of pollution under certain circumstances. Consider a situation in which the manager knows all parameters of the ecological system with zero error, and obtains annual measurements (with zero observation error) of all three ecological state variables. Assume that the manager knows the probability distribution of stochastic disturbances to the P input, but cannot know a particular disturbance until it has occurred. Thus, the manager can calculate a target proportion of P-intensive farms, by stochastic optimization of net discounted utilities over infinite time (Appendix 3), where the control variable is the proportion of P-intensive farms. Further, assume that farmers adjust instantaneously to the desired proportion of P-intensive farms. If the manager ignores the stochasticity of inputs, the net discounted value is maximized where the proportion of P-intensive farms is about 0.77 (Fig. 10A). If the stochasticity is included, net discounted value is maximized where this proportion is about 0.55. This reduction in the proportion of P-intensive farmers represents the "precautionary principle" evoked by environmental stochasticity (Carpenter et al. 1999). The size of the low-P attractor (Appendix 8) drops sharply when the proportion of P-intensive farms rises above 0.35, corresponding to the appearance of the high-P attractor (Fig. 10B). As the proportion of P-intensive farms rises, the size of the low-P attractor declines, reaching zero when the attractor vanishes at a proportion of P-intensive farms of about 0.83. The standard deviation of the load disturbance rises with the proportion of P-intensive farms, because of the lognormal distribution of the disturbances of P input (Fig. 10B). Distributions with long, unbounded tails for extreme events, such as the lognormal, are appropriate for many environmental disturbances (Walters 1986, Ludwig 1995, Carpenter et al. 1999). The manager using stochastic optimization will choose to set the proportion of P-intensive farms at 0.55, where the standard deviation of load disturbances is more than half as large as the width of the attractor. Thus, some disturbances will knock the system out of the low-P attractor into the high-P attractor, creating an outbreak like those in Fig. 7. We caution the reader that this is a numerical example. More work is needed to establish the conditions under which the outbreaks can occur. Nevertheless, this example shows that perfect knowledge and perfect control do not preclude the possibility of destabilizing this nonlinear, stochastic system. Note that realistic complications, such as imperfect knowledge of the structural model for the ecosystem, parameter uncertainty, failure to monitor the important ecological variables, observation error, variability in farmer behavior, and lags in implementing policy, are all likely to increase the potential for instability.
Models of the adaptive cycle?
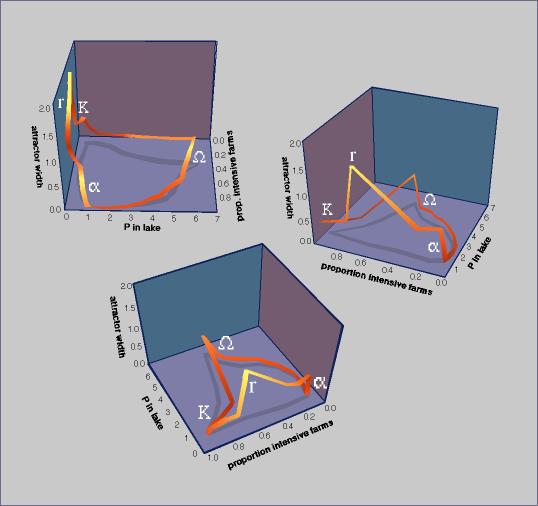
The patterns that emerge from these models resemble the adaptive cycle of Gunderson et al. (1995) in several respects. During the exploitation phase of the cycle (r to K of Fig. 11), human dependency, as measured by the proportion of phosphorus-intensive farms, grows to a high level. At the same time, the ecosystem is becoming more fragile because of the accumulation of phosphorus in upland soils and lake mud. These dynamics correspond the the exploitation phase, or r-to-K transition, of Gunderson et al. (1995). Eventually, an input event disturbs the ecosystem out of the desirable attractor, and phosphorus levels in the water move rapidly to the polluted state (Ω of Fig. 11). The manager attempts to stave off disaster by reducing the proportion of phosphorus-intensive farms, but it is too late: the high levels of phosphorus in soil and mud make eutrophication inevitable. This is the collapse or Ω phase. The low-phosphorus attractor vanishes for a period of time. During this time, there are massive adjustments in farm policy, causing drastic reduction in the proportion of phosphorus-intensive farms and gradual reductions in phosphorus levels in soil, mud, and lake water (α of Fig. 11). This is the learning or renewal (α) phase. These policies eventually cause the desirable attractor to re-appear. A new phase of exploitation (r of Fig. 11) is initiated.
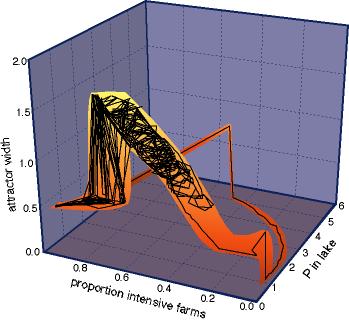
An adaptive manager would move toward sustainability by shrinking the scope of the cycles. A moderate proportion of phosphorus-intensive farms would be maintained and adjusted to bring soil phosphorus toward levels that reduce the risk of eutrophying the lake. Such policy experiments may be expensive, in the sense that they appear to be suboptimal economically (Walters 1997, Easley and Kiefer 1988), yet they are "safe" in the sense that they expand the desirable attractor and enable the manager to learn how the attractor responds to policy choice. Information gained from these experiments would be used to adjust policies, with the goal of sustaining both water quality and farming activity. Continual learning and continual adjustment become the norm. The result would be cycles of smaller amplitude, with generally low levels of lake water phosphorus, variable proportions of phosphorus-intensive farms, and moderately large attractor width. A crash, followed by several hundred years of exploratory, adaptive, sustainable management, is illustrated in Fig. 12.
It is important to recognize that sustainability cannot be achieved by seeking a fixed stable point. Frozen policy is a route to disaster. If policies are fixed, or experimental explorations of the stability domain are too timid, the manager cannot learn quickly enough to make the adjustments that are needed to sustain the social and ecological system. The consequences of narrow policies vs. adaptive ones are illustrated in the accompanying paper by Janssen and Carpenter (1999). Continual learning is crucial for sustainability. Such learning requires exploration of the stability domain. Such explorations carry some risk of moving the system out of a desirable domain, and therefore require careful consideration.
When should one be open to learning? Stable policies have advantages for efficiency, whereas experimentation and change carry risk. But without learning, massive collapse is certain. Our explorations of these models suggest that experiments should be frequent. Experiments should last long enough to intepret how the system is responding; then a different regime should be tried. It is useful to keep track of how the system responds to a particular sequence of policies; a change in the trajectory of response is an indication of shifting controls. We invite the reader to play with the computer programs provided with this paper to discover the consequences of different sequences of policies.
What do these model worlds tell us about sustainability of real ecosystems? Two insights are suggested. The first is the need for experimentation, learning, and adaptation. Ecosystem managers are unlikely to get things exactly right, but by continual learning, they may come close enough to sustain society and the ecosystems upon which we depend (Janssen and Carpenter 1999). Second, slow variables and their interactions with fast variables are the most important scientific information for sustainable management. Ecological research often focuses on fast variables, which can be understood efficiently on the time scales favored by funding agencies and academic institutions. Such research has made important contributions, and we do not imply that it should be abandoned. However, a much greater effort is needed to understand the slow variables that underpin ecosystem processes, such as geomorphology, pedogenesis, and evolution, and their links to ecosystem services such as production and nutrient regeneration at fast time scales.
More work is neededModels presented here are among the first to integrate nonlinear ecosystem dynamics at multiple time scales with dynamics of social and economic variables. We wish to emphasize that this important topic demands careful, extensive research. The present paper barely scratches the surface. The models presented here are exploratory, and may well have serious omissions or oversimplifications. For example, we would like to see models that address a greater range of ecological time scales, agents capable of inventing model structures during the learning process, agents capable of more forward-looking and adaptive behaviors, and effects of a diversity of signals with varying amounts of noise. Future work should carefully explore the conditions necessary for the dynamics illustrated here, and the dependency of the dynamics on particular assumptions of the simulations. Despite these cautions, we suggest that the models introduce an exciting area of interdisciplinary research that could prove vital to sustainability. We encourage the exploration of a wide range of alternative models that integrate nonlinear ecological dynamics, at slow and fast time scales, with complex social systems. We will be surprised if the models we have introduced here are not obsolete within a short period of time.
Computer programs and documentation may be downloaded in Appendix 9.
Responses to this article are invited. If accepted for publication, your response will be hyperlinked to the article. To submit a comment, follow this link. To read comments already accepted, follow this link.
We are very grateful to Pille Bunnell for graphics. Don Ludwig, Marco Janssen, and three referees provided helpful criticisms of earlier drafts. We thank participants in the Winona meeting of the Resilience Network for helpful comments on the simulations. This work was supported by the Pew Foundation, North Temperate Lakes LTER Site, and the Resilience Network.
Bennett, E. M., T. L. Reed, J. N. Houser, J. R. Gabriel, and S. R. Carpenter. 1999. A phosphorus budget for the Lake Mendota watershed. Ecosystems 1:69-75.
Brock, W. A. 1977. A polluted golden age. Pages 441-461 in V. L. Smith, editor. Economics of natural and environmental resources. Gordon and Breach, New York, New York, USA.
Brock, W. A., and S. N. Durlauf. 1999. A formal model of theory choice in science. Economic Theory, in press.
Brock, W. A., and C. H. Hommes. 1997. A rational route to randomness. Econometrica 65:1059-1095.
Carpenter, S. R., N. F. Caraco, D. L. Correll, R. W. Howarth, A. N. Sharpley, and V. H. Smith. 1998. Nonpoint pollution of surface waters with phosphorus and nitrogen. Ecological Applications 8:559-568.
Carpenter, S. R., and K. L. Cottingham. 1997. Resilience and restoration of lakes. Conservation Ecology 1(1):2. [online] URL: http://www.consecol.org/vol1/iss1/art2/
Carpenter, S. R., and P. R. Leavitt. 1991. Temporal variation in a paleolimnological record arising from a trophic cascade. Ecology 72:277-285.
Carpenter, S. R., D. Ludwig, and W. A. Brock. 1999. Management of eutrophication for lakes subject to potentially irreversible change. Ecological Applications 9, in press.
Dixon, J. A., L. F. Scura, R. A. Carpenter, and P. B. Sherman. 1994. Economic analysis of environmental impacts. Earthscan Publications, London, UK.
Easley, D., and N. Kiefer. 1988. Controlling a stochastic process with unknown parameters. Econometrica 56:1045-1064.
Grandmont, J. M. 1998. Expectations formation and stability of large socioeconomic systems. Econometrica 66:741-781.
Gunderson, L. H., C. S. Holling, and S. S. Light, editors. 1995. Barriers and bridges to the renewal of ecosystems and institutions. Columbia University Press, New York, New York, USA.
Heal, G. M. 1997. Discounting and climate change. Climatic Change 37:335-343.
Holling, C. S. 1973. Resilience and stability of ecological systems. Annual Review of Ecology and Systematics 4:1-23.
_______ , editor. 1978. Adaptive environmental assessment and management. Wiley, New York, New York, USA.
Holling, C. S., and A. D. Chambers. 1973. Resource science: the nurture of an infant. BioScience 23: 3-21.
Holling, C. S., and G. K. Meffe. 1996. On command-and-control, and the pathology of natural resource management. Conservation Biology 10:328-337.
Janssen, M. 1998. Modeling global change: The art of integrated assessment modeling. Edward Elgar, Lyme, Connecticut, USA.
Janssen, M., and S. R. Carpenter. 1999. Managing the resilience of lakes: a multi-agent modeling approach. Conservation Ecology. [online] URL: http://www.consecol.org/in press.
Lee, K. N. 1993. Compass and gyroscope. Island Press, Washington, D.C., USA.
Levin, S. A. 1992. The problem of pattern and scale in ecology. Ecology 73:1943-1967.
Lindley, D. V. 1985. Making dDecisions. Wiley, New York, New York, USA.
Ludwig, D. 1995. A theory of sustainable harvesting. SIAM Journal of Applied Mathematics 55: 564-575.
_______ . 1998. Report on mud and agent dynamics. Memorandum to the Resilience Network. University of Florida, Gainesville, Florida, USA.
Ludwig, D., B. Walker, and C. S. Holling. 1997. Sustainability, stability and resilience. Conservation Ecology 1(1):7. [online] URL: http://www.consecol.org/vol1/iss1/art7/
Marimon, R. 1989. Stochastic turnpike property and stationary equilibrium. Journal of Economic Theory 47:282-306.
NRC (National Research Council). 1993. Soil and water quality. National Academy Press, Washington, D.C., USA.
Novotny, V., and H. Olem. 1994. Water quality: prevention, identification and management of diffuse pollution. Van Nostrand Reinhold, New York, New York, USA.
Nürnberg, G. K. 1984. Prediction of internal phosphorus load in lakes with anoxic hypolimnia. Limnology and Oceanography 29:135-145.
Pole, A., M. West, and J. Harrison. 1994. Applied Bayesian forecasting and time series analysis. Chapman and Hall, New York, New York, USA.
Sargent, T. 1993. Bounded rationality in macroeconomics. Clarendon Press, Oxford, UK.
Scheffer, M., and J. Beets. 1994. Ecological models and the pitfalls of causality. Hydrobiologia 276:115-124.
Soranno, P. A., S. R. Carpenter, and R. C. Lathrop. 1997. Internal phosphorus loading in Lake Mendota: response to external loads and weather. Canadian Journal of Fisheries and Aquatic Sciences 54:1883-1983.
Walters, C. J. 1986. Adaptive management of renewable resources. Macmillan, New York, New York, USA.
_______ . 1994. Use of gaming procedures in evaluation of management experiments. Canadian Journal of Fisheries and Aquatic Sciences 51:2705-2714.
_______ . 1997. Challenges in adaptive management of riparian and coastal ecosystems. Conservation Ecology 1(2):1. [online] URL: http://www.consecol.org/vol1/iss2/art1/
Wilson, M., and S. R. Carpenter. 1999. Economic valuation of surface freshwater ecosystem goods and services in the United States 1971-1997: a methodological literature review. Ecological Applications 9, in press.