|
|
|
Copyright © 1999 by The Resilience Alliance*
The following is the established format for referencing this article:
Nowak, M. A. 1999. The mathematical biology of human infections. Conservation Ecology 3(2): 12. [online] URL: http://www.consecol.org/vol3/iss2/art12/
A version of this article in which text, figures, tables, and appendices are separate files may be found by following this link.
Perspective, part of Special Feature on McDonnell Centennial Essays The Mathematical Biology of Human Infections Martin A. Nowak
Institute for Advanced Study
- Abstract
- Replication
- Immunity
- Variation
- Treatment
- Virulence
- Prions
- Summary
- Responses to this Article
- Literature Cited
Humans are constant victims of infectious diseases. Biomedical research during this century has led to important insights into the molecular details of immune defense. Yet, many questions relating to disease require a quantitative understanding of the complex systems that arise from the nonlinear interactions between populations of immune cells and infectious agents. Exploration of such questions has lead to a newly emerging field of mathematical biology describing the spread of infectious agents both within and between infected individuals. This essay will discuss simple and complex models of evolution, and the propagation of virus and prion infections. Such models provide new perspectives for our understanding of infectious disease and provide guidelines for interpreting experimental observation; they also define what needs to be measured to improve understanding.
KEY WORDS: CTL response, HIV, antivirals, epidemiology, immune response, infectious diseases, mathematical biology, models of evolution, prions, resistance, treatment, viruses.
Published: November 10, 1999
Infectious diseases pose a complex and global threat to human populations. The numerous species of viruses, bacteria, and higher organisms that are able to infect humans have changed the course of history. In the 14th century, one in four people in Europe died from bubonic plague, a bacterial infection. In 1520, the Aztecs lost half of their population to smallpox, a virus supplied by the Spanish during their conquest of the New World. In 1918/1919, a worldwide epidemic of influenza virus killed about 20 million people. Nowadays, about one million children die every year from malaria, caused by a unicellular organism that grows primarily in red blood cells. The recent pandemic of the human immunodeficiency virus (HIV) has produced global concern and a greater awareness of infectious diseases in the affluent west. About 5 million people worldwide have died from AIDS so far, with an estimated 27 million infected now. In response to the high mortality associated with infectious illness, evolution has equipped humans with intricate biological defense mechanisms. The human immune system consists of about 1000 billion cells. Certain immune cells, named T cells, recognize foreign structures on the surface of other cells. They release substances that alert other immune cells or inhibit growth of infectious agents, or they kill virus-infected cells. Other immune cells, named B cells, release antibodies that bind to infectious agents and mark them for elimination. Macrophages are immune cells that digest bacteria or virus-infected cells. This century has witnessed tremendous advances in our understanding of the molecular biology of the immune system and how it fights against infections. Yet, many important processes are barely understood. For example, in the context of virus infections, there are crucial questions. What is the lifetime of a virus-infected cell in a patient? What proportions of infected cells are eliminated by the immune response before they can release new virus particles? How many virus particles are neutralized by antibodies? What governs the complex steady state among virus, uninfected cells, and various components of the antiviral immune response in persistent infections? How does virus evolution during individual infections affect disease development?
These questions have one common theme: they are of quantitative nature and they deal with the dynamics of populations of immune cells and infectious agents. In order to answer these questions, it is not sufficient to know what detailed molecular interactions exist between individual cells or molecules. One requires an understanding of the complex dynamics of infectious diseases based on precise mathematical models. In this essay, I will discuss how mathematical models, in conjunction with experimental data, can improve our understanding of infectious diseases. It will be shown how simple mathematical rules can explain complex patterns of infection dynamics. In addition, the increasing understanding of such biological systems also justifies development of more complex mathematical models designed to provide more detailed descriptions of the dynamics. The main part of this essay consists of six sections: Replication, Immunity, Evolution, Treatment, Virulence, and Prions. The text will be free of mathematical equations. Figures and figure legends will illustrate important mathematical concepts. Much emphasis will be given to HIV, because more quantitative data are available for HIV than for any other human virus infection.
Viruses infect cells; infected cells produce viruses. For example, HIV grows predominantly in certain white blood cells. The virus enters the cell by means of a specific interaction between the viral envelope protein and proteins on the surface of the cell. Virus and cell membranes fuse and the inner structure of the virus containing the virus genome enters the cell. The virus genome is only 10,000 bases long, compared to the 3 billion bases of the host cell genome. However, the virus will take over some essential functions of the host cell, manipulate it to produce more viruses, and ultimately induce the death of the cell. Following cell entry, the virus RNA genome is transcribed into DNA, which subsequently is inserted into the genome of the host cell. Using the genetic machinery of the host cell, the viral genome starts to generate virus proteins and new RNA copies of itself. Viral proteins and RNA combine to give rise to new virus particles, which are released from the cell. New virus particles then find new target cells and the process is repeated.
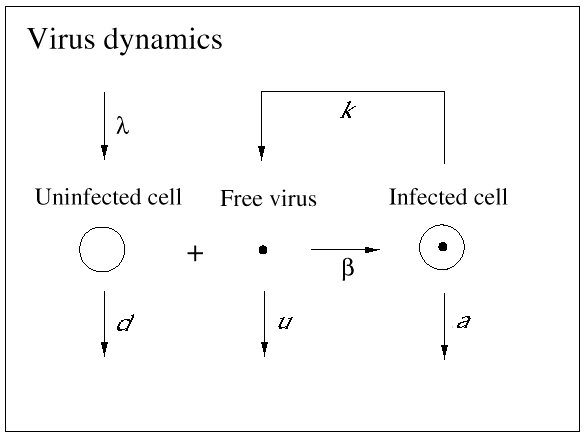
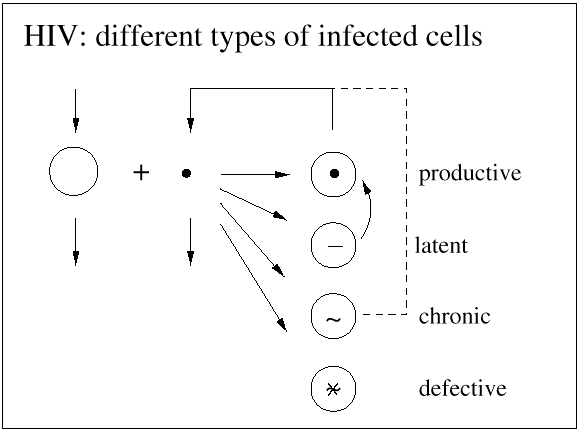
The basic mathematical model of virus dynamics includes three time-dependent variables: uninfected cells, infected cells, and virus particles. Virus particles invade uninfected cells and transform them into infected cells. Infected cells produce new virus particles. Uninfected cells, infected cells, and virus particles die at certain rates. Furthermore, we assume that uninfected cells are continuously being produced by the body (Fig. 1).
Fig. 1.The basic model of virus dynamics. The abundances of uninfected cells, infected cells, and free virus are given by x, y, and v, respectively. Uninfected cells are
produced at a constant rate,  . Free virus infects uninfected cells at the rate . Free virus infects uninfected cells at the rate 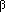 xv.
Infected cells produce free virus at the rate ky. Uninfected cells, infected cells, and free virus die at the rates dx, ay, and uv, respectively. These assumptions lead to the
following system of three differential equations: xv.
Infected cells produce free virus at the rate ky. Uninfected cells, infected cells, and free virus die at the rates dx, ay, and uv, respectively. These assumptions lead to the
following system of three differential equations:
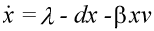 (1) (1)
|
The number of virus particles released from one infected cell is referred to as the ''burst size.'' Viruses usually are not very efficient; a large fraction of virus particles budding from a cell may not be functional. Among those that are functional, only a subset will infect new cells. The ''basic reproductive ratio,'' R0, of a virus infection is defined as the number of secondary infected cells that arise from any one infected cell at the beginning of the infection (when most cells are uninfected). Clearly, if R0 is larger than one, then a ''chain reaction'' will lead to an explosive increase in virus abundance. The number of infected cells will grow exponentially at first (at a rate proportional to R0); after some time, the abundance of uninfected cells will decline and virus growth will slow down. Virus abundance, therefore, reaches a peak value and subsequently declines to a constant equilibrium value. If R0 is less then one, the infection cannot spread; the host is not susceptible to infection. In light of the model, the aim of any vaccine should be to boost the initial antiviral immunity in order to reduce the value of R0 below one (Fig. 2).
This basic model of virus dynamics has been used to fit data on virus load decline in HIV-infected patients receiving antiviral therapy. As a result, it has been estimated that the half-life of HIV-infected cells in patients must be about 2 days and the half-life of virus particles must be significantly shorter than this (Coffin 1995, Ho et al. 1995, Wei et al. 1995, Perelson et al. 1997). These findings came as a big surprise to most immunologists, because a prevailing view was that HIV is rather inactive during the long asymptomatic period. The numbers imply that about 30% of virus-infected cells are replaced every day. The generation time of HIV is about 2 days, which means that the virus goes through 1500 generations in a typical 10-yr incubation period. (By comparison, there have been only about 30 human generations in the last millenium.)
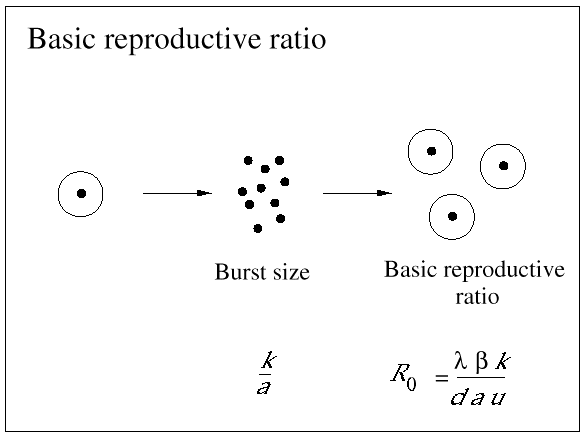
Nevertheless, not all HIV-infected cells in a patient are short-lived. The precise statement is that those cells that produce most plasma virus have a half-life of about 2 days. In fact, most HIV-infected cells are long-lived. Around 90% of infected cells contain nonfunctional HIV genome and live for about 100 days (which is close to the half-life of the uninfected cell). There is another subset of infected cells that harbor virus in a latent state. The half-life of these latently infected cells turns out to be around 10-40 days (Fig. 3).
Virus infections are opposed by immune responses. In HIV-infected patients, specific antibodies bind to virus particles and prevent them from infecting cells. Cytotoxic T lymphocytes (CTL) recognize viral peptides on the surface of infected cells. In response to such an encounter, they become activated, start to divide, and release substances that prevent virus replication. In addition, they can directly eliminate infected cells. CTL are highly specific; they recognize only specific viral peptides that are bound to human leukocyte antigens (HLA) on the surface of cells. Such a peptide is typically 10 amino acids long. A viral protein may contain a few hundred amino acids and may have several peptides that are recognized by CTL. Peptides recognized in this way are called ''epitopes.'' Mathematical equations for immune responses can be added to the basic model of virus dynamics. For example, a CTL response is described by the following assumptions: infected cells are killed at a rate proportional to the abundance of CTL; CTL are stimulated to replicate at a rate proportional to the abundance of infected cells; in the absence of further stimulation, CTL die. The model introduces the new concept of ''CTL responsiveness,'' which is defined as the rate at which a given number of infected cells stimulates proliferation of a specific CTL response. Patients may differ in their CTL responsiveness to a virus. An interesting and counterintuitive result of the model is that patients with different CTL responsiveness may have a similar equilibrium abundance of CTL, but may differ greatly in their virus load: a good responder has a low virus load, whereas a weak responder admits a high virus load (Nowak and Bangham 1996).
A virus like HIV contains 10-30 epitopes that can be seen by a patient's CTL. Nevertheless, a common observation is that the immune response concentrates its forces against a single epitope. This phenomenon is called ''immunodominance.'' Mathematical models can explain immunodominance. In simple terms, CTL responses against different epitopes are not independent of each other, but compete for antigenic stimulation. As a particular CTL response increases in abundance, it down-regulates the virus population and therefore reduces the antigenic stimulation experienced by all CTLs. An equilibrium is reached in which the most immunogenic epitope elicits the dominant response. CTL responses to other epitopes will be absent or at low frequencies.
Both mathematical results in this section are reminiscent of well-known phenomena in ecology (May 1974, Levin et al. 1997). The analogy becomes clear if virus-infected cells are seen as prey and CTL as predators: virus replicates, CTL grow, stimulated by virus, and CTL kill virus-infected cells. In simple ecological models, a more efficient predator does not necessarily achieve a higher equilibrium abundance, but causes lower equilibrium values of prey. This is equivalent to the result that a patient with a stronger immune responsiveness may not end up with a higher abundance of CTL, but rather with a lower virus load. Furthermore, immunodominance is reminiscent of competitive exclusion. In the absence of confounding effects, only one type of predator can survive for one specific type of prey. In fact, the interaction among different types of susceptible host cells, immune cells, and virus particles has many parallels to the complexity found in ecosystems.
Infectious agents have shorter generation times than their hosts, and their reproduction is more inaccurate. Therefore, they can accumulate genetic changes at very fast rates. Such rapid genetic variation enables HIV to respond quickly to any selection pressure that it encounters during an infection. For example, HIV can generate ''antigenic variants'' that escape from specific immune responses. A single amino acid substitution can be sufficient to prevent a viral epitope from being recognized by the patient's CTL (McMichael and Phillips 1997).
The mathematical theory of antigenic variation (Nowak et al. 1991) predicts that viruses carrying the mutant epitope will increase in abundance because they have a selective advantage. As the frequency increases, the immune system may be stimulated to mount a new response that is specific for the mutated epitope. Another possibility, however, is that the immune system will not respond to the mutated epitope, but instead will shift to a completely different epitope that previously did not elicit a response. Thus, antigenic variation can cause shifting immune responses to alternative epitopes. Because, in the absence of antigenic variation, the theory predicts a dominant response against the strongest (most immunogenic epitope), the consequence of antigenic variation is to divert the immune response to weaker epitopes. Such ''shifting immunodominance'' can be accompanied by chaotic oscillations in the freuqency of virus mutants and the magnitude of the immune response to individual epitopes (Nowak et al. 1995, Nowak and McMichael 1995).
Several results of this theory have been confirmed by observations. In individual patients, there can be fluctuating CTL responses against various viral epitopes, accompanied by irregular oscillations in virus mutant frequencies. In the event of antigenic escape in one epitope, several research groups have found shifts in the overall immune response to other epitopes (Borrow et al. 1997).
On average, HIV-1 infected patients live for about 10 years following infection, but the range varies from six months to more than 20 years. An important question of HIV research is concerned with the mechanism of disease progression. Given that the daily turnover of the virus is so rapid, why does it take so many years from infection to death? Mathematical models of HIV infection have led to the idea that disease progression may be a consequence of virus evolution during individual infections. In any one infected patient, the virus undergoes continuous genetic variation that generates an increasing number of different virus variants. The immune system may find it harder and harder to mount responses against these newly emerging virus variants. This evolutionary race between the virus and the immune system can slowly tip the balance of power between the immune system and the virus in favor of the virus. Once the antigenic diversity of the virus population has increased above a threshold value, the immune system can no longer control the virus. More generally, the idea is that every single HIV infection has to be seen as an evolutionary process in which the virus population constantly changes and new virus mutants continuously emerge. Natural selection will favor virus variants that are able to escape from immune responses, or with increased rates of replication, or with the ability to infect a greater variety of cell types in the human body. The theory clearly shows that all of these evolutionary changes have the same consequence: they increase overall virus abundance in the patient. It is well known that HIV disease is related to virus abundance; therefore, virus evolution during individual infections may drive disease progression.
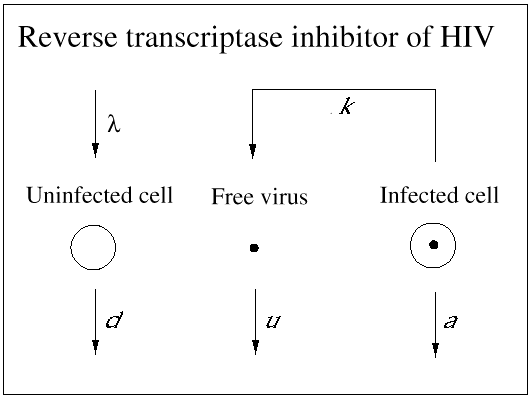
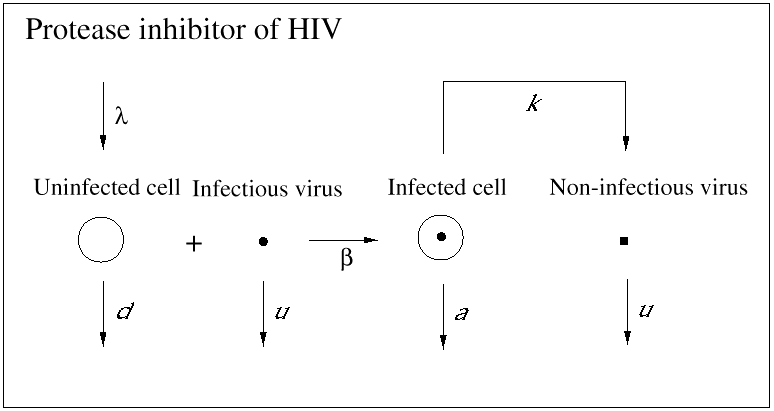
An important contribution of biomedical research in this century was the discovery of antibiotics, which effectively inhibit reproduction of bacteria. As a consequence, many otherwise fatal bacterial infections could be treated. Until recently, however, no potent medication was available against viral infections. (A prominent exception is acyclovir, which inhibits herpes simplex virus.) In 1989, it became clear that a drug called zidovudine, which was originally developed against cancer, was effective against HIV. Clinical trials showed that the drug increased the life expectancy of AIDS patients by about 6 months. The drug works as an inhibitor of the reverse transcriptase, which is a viral enzyme that rewrites the genetic information of HIV from the RNA into the DNA alphabet. Unfortunately, the beneficial effect of the drug is only short-lived, because the virus rapidly develops resistance: mutations in the reverse transcriptase gene can render the enzyme insensitive to inhibition by the drug. Thus, the virus can escape from drug treatment in a way that is similar to its escape from immune responses. More recently, further anti-HIV drugs have been developed. Some of the new drugs are reverse transcriptase inhibitors, and others are directed against the viral protease, an enzyme essential for the formation of infectious virus particles from infected cells. All anti-HIV drugs prevent the virus from reproducing: they do not kill virus particles or infected cells (Figs. 4 and 5).
Essentially, all of these drugs, if used as single antiviral therapy, lead to the emergence of resistant virus mutants. The pattern is often similar. Initially, there is a decay in virus abundance, but after some time, the virus resurges. The decisive treatment breakthrough was to combine several drugs at once. For about 2 years, this combination therapy has proved to be a tremendous success. In many patients, virus abundance in the blood decays below detection limit within weeks of treatment and can remain undetectable for years.
Mathematical models have been developed to describe the dynamics of resistance in order to understand the factors that determine when and if resistant virus will emerge in a patient. The mathematical theory also provides a definition of viral resistance. Earlier, I mentioned the basic reproductive ratio, R0, as a measure of the intrinsic growth potential of the virus. Let us now apply this notion to individual virus mutants and let us consider a patient who has just started on antiviral treatment. A particular virus mutant is resistant to therapy if its R0 value during therapy exceeds one. Such a mutant will not decline to zero abundance, but will persist during treatment. Therefore, resistance is not simply determined by the susceptibility of the virus mutant to inhibition by the drug, but by its intrinsic growth rate (or fitness) during antiviral therapy. An important consequence of this notion is that resistance is not only a property of the virus, but also a combined property of virus and host (Bonhoeffer et al. 1997). A particular virus mutant may be resistant in a patient with a weak immune response and may be eliminated in a patient with a strong immune response. Furthermore, test tube measurements of levels of inhibition by various drug concentrations are not sufficient to determine whether a particular virus mutant will be resistant to antiviral therapy.
Mathematical models show that the main problem of resistance is whether or not resistant virus mutants are present in a patient prior to treatment. Treatment will work if the R0 values of all virus mutants present in a patient at the time when therapy starts are below one. An interesting mathematical result is that the probability that a particular mutant will emerge during effective therapy is less than the probability that this mutant was already present before treatment. Therefore, treatment must be designed to minimize the probability that resistant variants exist in a patient at the time when treatment commences. This can be achieved by treating patients early in infection, when virus load and diversity are low and the immune system remains intact. In addition, it is essential to use many drugs at once, because a virus that is resistant to several drugs simultaneously will require many specific mutations. In fact, the more drugs are deployed, the better the chances of success. Of course, the limiting conditions will be the adverse side effects and the cost of therapy. Thus, mathematical models support the notion of ''treating hard and early.''
Combination therapy provides a first dramatic success in fighting HIV, but it is clear that it will not solve the global HIV epidemic. Most HIV infections occur in developing countries that cannot afford the expensive new antivirals. Some African countries have a health budget of one dollar (U.S.) per person per year, whereas costs of multiple-drug therapy are estimated at U.S.$10,000 per person per year. It seems unimaginable at the moment that HIV-infected patients in these countries will ever benefit from combination therapy.
Furthermore, as more patients are treated, resistant viruses will become more common. This will initiate an arms race between pharmaceutical companies searching for new drugs and the virus mutating away from them. A similar battle, it seems, is currently been lost against bacteria. Antibiotic resistance has become more and more widespread, and the pharmaceutical researchers find it harder and harder to come up with new drugs. It is likely that the next few decades will see increasing numbers of untreatable bacterial infections.
The coevolution of infectious agents and their hosts is one of the most fascinating fields of modern evolutionary theory. Mathematical models lie at the interface between evolution, ecology, and immunology. One of the most debated questions is how natural selection shapes the level of virulence of parasites. Here, ''virulence'' denotes the mortality of the host as a consequence of infection, and ''parasite'' is taken to include viruses, bacteria, and all other infectious agents. Conventional wisdom understood that well-adapted parasites should become harmless, because the parasite does not benefit by killing the host on which its own reproduction depends. However, mathematical models, developed by Robert May and Roy Anderson, have forced us to rethink this oversimplified view (Anderson and May 1991). The evolutionary success of a parasite mutant depends on its basic reproductive ratio, R0. Here, R0 denotes the intrinsic growth rate of the parasite in the population of hosts, that is, the number of secondary infected individuals that arise from any one infected individual (when almost all individuals are uninfected). If there are several parasite mutants circulating in the host population, then the mutant with the highest R0 will win. It is conceivable that, for example, a higher parasite load in an infected individual may increase the transmissibility of the parasite to other hosts, but may also cause a higher degree of virulence. In this case, natural selection may settle for a trade-off between virulence and transmissibility. Evolution will maximize R0, but will not necessarily lead to low virulence. In fact, field studies have revealed many examples of ancient host-parasite systems that have not led to avirulence.
The original May-Anderson approach does not allow for the possibility that one host individual is infected by more than one parasite mutant. Recent work in the field, however, has concentrated on exactly this question (Nowak and May 1994). It has been shown that superinfection (that is when a previously infected host is infected by another parasite mutant) or evolution of the parasite during individual infections usually leads to higher degrees of virulence, even at the expense of reducing the parasite's overall transmission potential. There are also interesting results with respect to the evolution of parasite diversity: the classical framework suggests that only one parasite strain can survive, but superinfection leads to complex dynamics and a stable coexistence of many parasite strains. In this scenario, parasite diversity accumulates roughly as a logarithmic function of time. Reducing host abundance reduces parasite diversity, with the most virulent strains dying out first. Therefore, vaccinating a subset of a host population can reduce the overall virulence of a disease. The mathematical models have interesting parallels to the general question of biodiversity and metapopulation dynamics in ecology. In fact, the same mathematical equations have been derived by David Tilman to explore complex questions in species diversity and the dynamics of habitat colonization (Tilman et al. 1994).
As the human species becomes more abundant on the globe and interactions between humans become more frequent, more infectious agents will find opportunities to cross from their host species to humans and to spread within the human population. For example, HIV is thought to have spread extensively in Africa (and from there to the rest of the world) only in the last few decades. HIV has most likely arisen from related monkey viruses, which are believed to be millions of years old. Over the last several thousand years, humans must have been exposed to these monkey viruses and individual people must have become infected. It is likely that these viruses did not grow well in humans, and infected people may have transmitted the virus only to a few other people before the chain of infection died out again. As population densities and social interactions among people increased, the virus found greater opportunities to infect humans and to spread among human hosts, which led to a rapid evolutionary adaptation of the virus to become a specific human virus.
The recent epidemic of bovine spongiform encephalopathy, BSE (''mad cow'' disease), among British cattle and the subsequent emergence of a new form of Creutzfeldt Jakob disease (CJD) in humans is another example of an unforeseen encounter between humans and an infectious disease of another species. Both of these diseases are caused by prions, which are perhaps the most bizarre infectious agents (Prusiner 1997). Smaller than viruses, they appear to contain only protein, and no nucleic acid. They do not transmit their genetic information from one host to another; the genetic information is already present in the host. We all have the prion gene. It encodes for a protein that is present in nerve cells and cells of the immune system. Its natural function is unknown. According to the ''prion hypothesis,'' the infectious agent is a malformed configuration of this protein. The diseased form interacts with the healthy form to induce a conformational change of the healthy into the diseased form.
It is now known that the prion protein is involved in a number of human and animal diseases such as CJD and kuru of humans, scrapie of sheep, and BSE of cattle. These diseases are neurological maladies in which brain function is destroyed as neurons die and the brain tissue develops sponge-like holes. The human disease kuru, which attracted much public interest, is thought to have been transmitted from infected corpses by cannibalism. The route of transmission of scrapie, a wasting disease of sheep and goats, has never been identified. The recent epidemic of BSE in the United Kingdom has been attributed to feeding cattle with infected ruminant-derived protein. Around 170,000 infected cattle have died from BSE and up to 1 million potentially contaminated cattle have entered the human food chain. A new variant of CJD was found in the United Kingdom and is thought to be linked to BSE. About 20 human cases have been reported so far.
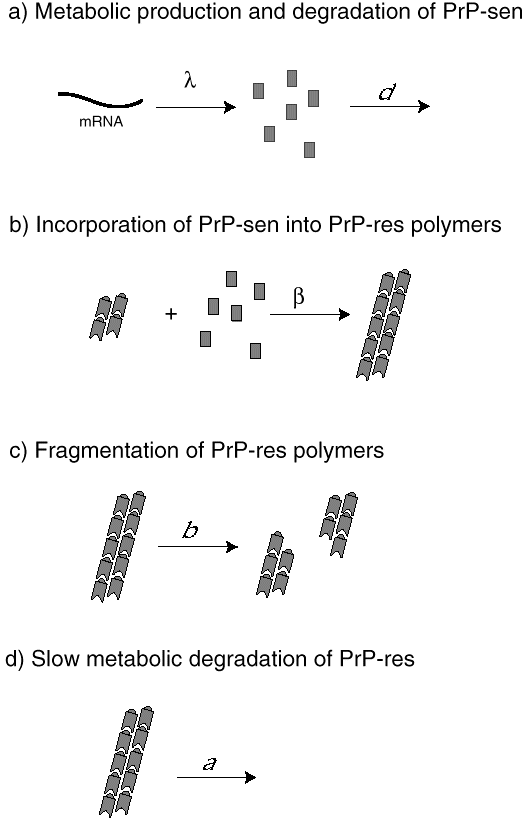
We have developed mathematical models of prion infection dynamics in order to understand how a protein alone can act as an infectious agent (Nowak et al. 1998). The basic idea is that prion replication and conformational change is a consequence of protein aggregation. The healthy conformation of the prion protein is called PrP-sen, which stands for protease-sensitive prion protein. The malformed conformation is called PrP-res, denoting protease-resistant prion protein. (The notation is based on the observation that PrP-res, but not PrP-sen, is resistant to digestion by certain proteases.) The mathematical models assume that PrP-sen exists as a protein monomer and is produced by the genetic machinery of the cell. PrP-res occurs as an aggregate. Infection is caused by small protein aggregates (nucleation seeds), which can grow by incorporation of new PrP-sen monomers. PrP-res aggregates break up to provide new nucleation seeds. The underlying mathematical equations represent a novel form of infection dynamics. The multiplication of PrP-res is a consequence of a continuous production of PrP-sen, which become incorporated into growing aggregates of PrP-res. Breakage of these aggregates increases their number (Fig. 6).
The model gives rise to an exponential increase in PrP-res abundance following infection with nucleation seeds. During the exponential growth phase, the PrP-sen concentration remains at its pre-infection equilibrium level and the average size of PrP-res aggregates is high. Subsequently, the PrP-sen levels start to decline as all of PrP-sen becomes incorporated into aggregates. PrP-res abundance saturates at high levels and aggregate sizes decline. The model shows which parameters determine whether a prion infection can take place and the relevant time scales.
A puzzling observation of prion biology is that different prion strains can be propagated indefinitely in the same animal host. In other words, if infectious prion particles are transferred from humans, cattle, or sheep to mice, then infection of the same group of inbred mice leads to different (but characteristic) incubation periods and to different (but characteristic) spatial distributions in the brain related to the host from which they were sampled. These ''prion strains'' are based on the same amino acid sequence, which is determined by the host, but are believed to have different conformations. Therefore, the biological characteristic of the prion strain must reside in the protein structure, not in the amino acid sequence. A given PrP-res molecule has to exist in one healthy and several (maybe 10) specific diseased conformations. Each of the diseased conformations must be able to interact with the healthy conformation in such a way as to reproduce its own conformation. According to the aggregation model of prion propagation, it is conceivable that the molecular structure of the growing PrP-res aggregates is dictated by the conformation of the infecting nucleation seeds. Thus, the same PrP-sen monomers can adopt different conformations when bound into aggregates that were initiated by different nucleation seeds; the structure of the nucleus is preserved, although the amino acid sequence of the monomers may differ.
In addition, PrP-sen molecules in different regions of the brain may have the same amino acid sequence, but may differ in their sugar residues, which are added to the protein after its production. It is known that about 20% of the molecular mass of the prion protein consists of sugar residues. It is conceivable that certain PrP-res aggregates can only react with a specific subset of the different types of PrP-sen molecules and induce their conversion into PrP-res. This model can explain why strains breed true and can also account for the specific spatial distribution in the brain of prion strains: the different types of PrP-sen may have specific spatial distributions in the brain of uninfected animals.
The new mathematical models of prion infection dynamics by protein aggregation are likely to be of wider significance than merely describing prion diseases. Protein aggregation in the central nervous system is also thought to be important for diseases like Alzheimer's, Parkinson's, Down's syndrome, and for general senescence.
During this century, the application of mathematical models to infectious disease has consisted of describing their spread through human populations. This has led to the classical branch of mathematical biology called epidemiology. More recently, advances in molecular techniques have generated information on how microbes grow within infected hosts, how they change their genetic structure, and the ways in which they interact with the immune system. This wealth of biological data has led to a new kind of mathematical epidemiology that deals with the complex dynamics of infectious agents within infected individuals. A dramatic success of this new discipline has been the quantification of HIV turnover rates in infected patients, using data from antiviral therapy.
Future developments in this field will see increasing efforts to understand the population genetics of infectious agents. Models of viral evolution during single infections are discussed in this essay. A major threat to human health in the next century will be microbial drug resistance. In this field, mathematical models present clear concepts and guidelines for further collection and analysis of data. Finally, mathematical models of the complex interaction between replicating infectious agents and the immune system will allow immunologists to employ more quantitative approaches to their data, such as in the measurement of turnover rates and the exact abundances of certain immune cell types. This empirical framework will be essential when seeking to determine the precise rate of elimination of infectious agents by specific immune responses, thereby establishing the foundations for a quantitative immunology.
Responses to this article are invited. If accepted for publication, your response will be hyperlinked to the article. To submit a comment, follow this link. To read comments already accepted, follow this link.
Anderson, R. M., and R. M. May. 1991. Infectious diseases of humans. Oxford University Press, Oxford, UK.
Bonhoeffer, S., R. M. May, G. M. Shaw, and M. A. Nowak. 1997. Virus dynamics and drug treatment. Proceedings of the National Academy of Sciences (USA) 94: 6971- 6976.
Borrow, P., H. Lewick, X. Wei, et al. 1997. Antiviral pressure exerted by HIV-1-specific cytotoxic T lymphocytes (CTLs) during primary infection demonstrated by rapid selection of CTL escape virus. Nature Medicine 3: 205-211.
Coffin, J. M. 1995. HIV population dynamics in vivo: implications for genetic variation, pathogenesis, and therapy. Science 267: 483-489.
Ho, D. D., A. U. Neumann, A. S. Perelson, W. Chen, J. M. Leonard, and M. Markowitz. 1995. Rapid turnover of plasma virions and CD4 lymphocytes in HIV-1 infection. Nature 373: 123-126.
Levin, S. A., B. Grenfell, A. Hastings, and A. S. Perelson. 1997. Mathematical and computational challenges in population biology and ecosystems science. Science 275: 334-343.
May, R. M. 1974. Stability and complexity in model ecosystems. Second edition. Princeton University Press, Princeton, New Jersey, USA.
McMichael, A. J., and R. E. Phillips. 1997. Escape of human immunodeficiency virus from immune control. Annual Review of Immunology 15: 271-296.
Nowak, M. A., R. M. Anderson, A. R. McLean, T. Wolfs, J. Goudsmit, and R. M May. 1991. Antigenic diversity thresholds and the development of AIDS. Science 254: 963-969.
Nowak, M. A., and C. R. M. Bangham. 1996. Population dynamics of immune responses to persistent viruses. Science 272: 74-79.
Nowak, M. A., D. C. Krakauer, A. Klug, and R. M. May. 1998. Prion infection dynamics. Integrative Biology 1: 3-15.
Nowak, M. A., and R. M. May. 1994. Superinfection and the evolution of virulence. Proceedings of the Royal Society of London B 255: 81-89.
Nowak, M. A., and A. J. McMichael. 1995. How HIV defeats the immune system. Scientific American 273: 58-65.
Nowak, M. A., R. M. May, R. E. Phillips, S. Rowland-Jones, D. G. Lalloo, S. McAdam, P. Klenerman, B. Köppe, K. Sigmund, C. R. M. Bangham, and A. J. McMichael. 1995. Antigenic oscillations and shifting immunodominance in HIV-1 infections. Nature 375: 606-611.
Perelson, A. S., P. Essunger, Y. Cao, M. Vesanen, A. Hurley, K. Saksela, and M. Markowitz. 1997. Decay characteristics of HIV-1- infected compartments during combination therapy. Nature 387: 188-191.
Prusiner, S. B. 1997. Prion disease and the BSE crisis. Science 278: 245-251.
Tilman, D., R. M. May, C. L. Lehman, and M. A. Nowak. 1994. Habitat destruction and the extinction debt. Nature 371: 65-66.
Wei, X., S. K. Ghosh, M. E. Taylor, V. A. Johnson, E. A. Emini, P. Deutsch, J. D. Lifson, S. Bonhoeffer, M. A. Nowak, B. H. Hahn, M. S. Saag, and G. M. Shaw. 1995. Viral dynamics in HIV-1 infection. Nature 373: 117-122.
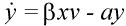 (2)
(2)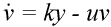 (3)
(3)
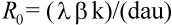 (4)
(4)
 (5)
(5)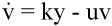 (6)
(6)