Animal Dispersal in Fragmented Habitat: Measuring Habitat Connectivity, Corridor Use, and Dispersal Mortality

Lesley Brooker, Michael Brooker, and Peter Cale

• Abstract
• Introduction
• Simulation Model
  • Landscape
  • Movement Algorithm
  • Assumptions and Rationale of the Model
  • Theoretical Example
• Field Study
• Data Analysis
• Application of the Simulation Model
  • Quantifying Corridor Use
  • Estimating Dispersal Mortality Rate
  • Comparing Dispersal Qualities of Landscapes
• Discussion
• Responses to this Article
• Acknowledgments
• Literature Cited
• Appendices
• Appendix 1. Demonstration version of the model
• Appendix 2. Technical details

We used a spatially explicit dispersal simulation to generate movement frequencies and distances for comparison with real dispersal frequencies collected in the field from two habitat-specific, sedentary bird species. The relationship between these two data sets allowed us to (1) test the hypothesis that the study species used corridor routes during dispersal; (2) measure the degree of reliance on corridor continuity; (3) estimate the rate of dispersal mortality with respect to distance traveled, and (4) give examples of how the model can be used to assess habitat connectivity with respect to similarly behaved species. We found that Blue-breasted Fairy-wrens and White-browed Babblers both used corridor routes during dispersal. Blue-breasted Fairy-wrens were inhibited by gaps greater than about 60 m, whereas White-browed Babblers crossed gaps of at least 270 m wide. For each species, the rate of dispersal mortality per unit distance traveled was about the same. Because we have effectively partitioned the risk of dispersal mortality from the chance of outside dispersal, and because our mortality estimates are model dependent but landscape independent, they can be transported to other landscapes on which simulations have been run and, therefore, can be used in population viability assessment of unstudied or hypothetical animal populations.

KEY WORDS: animal dispersal, Blue-breasted Fairy-wren, dispersal model, dispersal mortality, fragmentation, habitat connectivity, Malurus pulcherrimus, Pomatostomus superciliosus, spatially explicit dispersal, vegetation corridors, White-browed Babbler.

Published March 15, 1999.

The survival probability of species in small, isolated subpopulations depends, in part, on their ability to disperse. If animals are habitat specific, metapopulation persistence may also depend on the existence of corridors of suitable vegetation linking the otherwise isolated habitat patches in which these animal subpopulations live. Yet, there is very little information about which animal species actually use vegetation corridors during dispersal (but see, e.g., Cale 1990, Arnold et al. 1991, Saunders and de Rebeira 1991, Hinsley et al. 1995, Bentley and Catterall 1997, Desrochers and Hannon 1997), or about how effective differently connected landscapes may be for species with a range of different dispersal behaviors (Lynch and Saunders 1991, Lindenmayer et al. 1994, Ruefenacht and Knight 1995, Andreassen et al. 1996a , b, Rail et al. 1997). For example, a landscape with corridor gaps (discontinuities) of 100 m may be perfectly satisfactory for a large parrot that needs only visual contact to move from patch to patch (Saunders and de Rebeira 1991), but useless for a small arboreal lizard if that lizard never moves far from the safety of trees (Sarre et al. 1996).

In recent years, many different spatially explicit models have been developed for simulating animal dispersal in heterogeneous landscapes. Various modeling strategies have been employed (reviewed by Johnson et al. 1992, Schippers et al. 1996) including grid-based diffusion-like algorithms, GIS models involving landscape resistance, random walks, neutral landscape models, and individual-based local-rule models. Only the individual-based models can be used to estimate the probability that a disperser will reach a target site, taking into account peculiar dispersal behaviors with respect to different-sized corridor gaps. However, most existing individual-based models are quite complex, requiring sometimes arbitrary estimates to be made for several model parameters. Ruckelshaus et al. (1997) suggest that less detailed models would improve the match between model complexity and the quality of the available data.

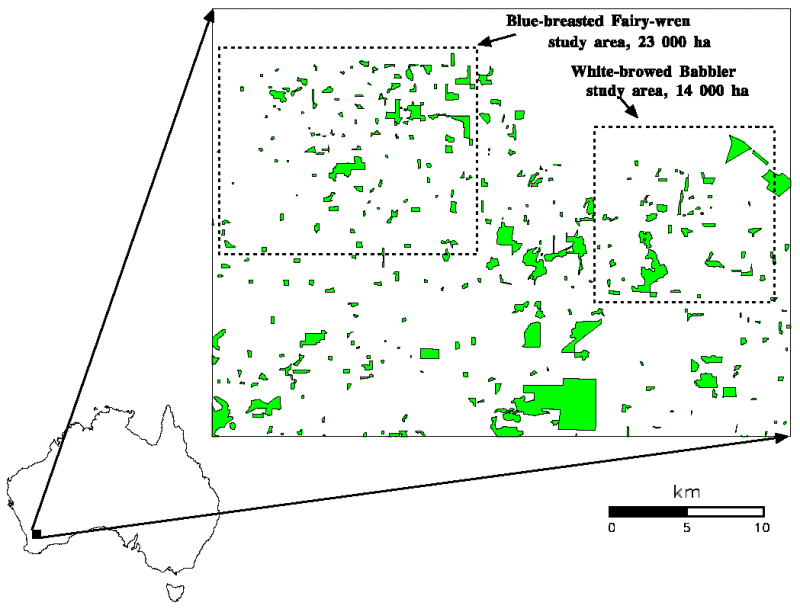
The Western Australian Wheatbelt is characterized by some of the most highly fragmented native vegetation in the world. In the Kellerberrin area (31^o38' S, 117^o43' E), 93% of the landscape has been cleared for agriculture in the last 100 years (Brooker and Margules 1996), leaving only small islands and linear strips of native vegetation marooned in what, for many native species, is a hostile "ocean" of agricultural crops and open pasture (Fig. 1).

Fig. 1. Respective locations of the Blue-breasted Fairy-wren study area (17 km x 13 km) and the White-browed Babbler study area (12 km x 12 km) , situated to the north of Kellerberrin, Western Australia.

Here, we present a simple methodology allowing us to test the hypothesis that dispersing species in the Kellerberrin landscape actually used corridor routes (i.e., dispersed through native vegetation rather than agricultural land). A computer model is used to simulate dispersal frequencies and distances, which, in turn, are matched against real dispersal frequencies collected from two bird species, the Blue-breasted Fairy-wren Malurus pulcherrimus and the White-browed Babbler Pomatostomus superciliosus (Fig. 2). By comparing these two data sets, we are able to (1) quantify corridor use (the degree of reliance on corridor continuity), (2) make an estimate of dispersal mortality with respect to simulated distance, and (3) compare the dispersal qualities of different landscapes.

Fig. 2. Male full-plumage Blue-breasted Fairy-wren (left) and White-browed Babblers (right). Photographs by G. Chapman.

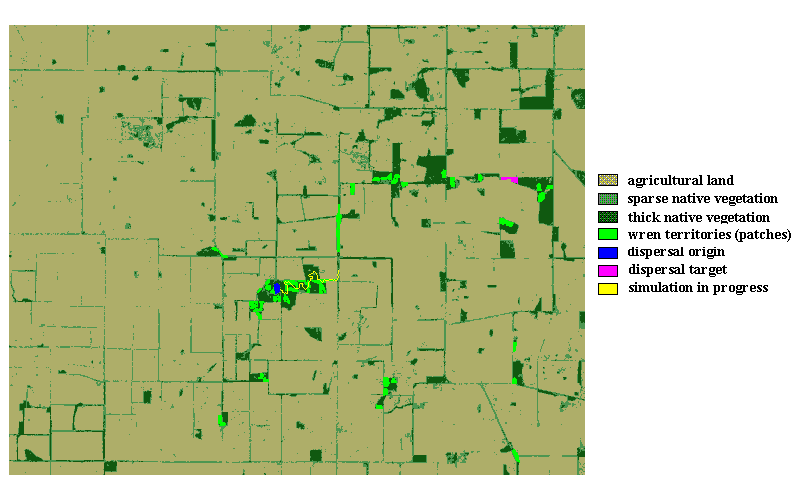
We developed a simple, spatially explicit, individual-based, local-rule dispersal simulation (see Appendix 1 for demonstration version) to (1) display a color-coded representation of a study landscape (Fig. 3); (2) simulate random-like movement through native vegetation, conforming with a use-defined gap tolerance; (3) record the number of times out of 100 iterations that a disperser, d, reaches a target destination during simulation; (4) record the median distance traveled by successful dispersers; and (5) record the straight line distances between patches.

Fig. 3. Screen display of Blue-breasted Fairy-wren study landscape showing the simulation in progress. The landscape is composed of native vegetation and agricultural land. Dispersals occur between pairs of patches, with each patch representing an actual wren breeding territory. The yellow trail represents the path taken during one iteration of a rule-based random-type walk, from a designated origin (blue) to a designated target (purple) with a 10,000-step "time" limit. After 100 iterations for this patch pair, the program records to a file the number of times the disperser d reached the target, the median distance traveled during successful dispersals (iterations), and the straight-line distance between origin and target.

Landscape

The landscape is represented by a grid of 30 x 30 m cells, with each cell (i.e., pixel) color coded to indicate either native vegetation or agricultural land (see Appendix 2 for technical details of image production). Simulated movements occur between patch pairs (i.e., a pair of patches representing dispersal origin and dispersal target), in which each patch represents a known bird breeding territory located in the native vegetation. For the purposes of the model, a "corridor" is considered to be any native vegetation linking a patch pair. This means that corridors are not necessarily narrow linear strips or separate entities.

Movement algorithm

In the simulation, d moves randomly through the remnant vegetation from a designated origin to a designated target, with a "time" limit (10 000 steps in the following examples, in which one cellular step represents 30 m). The value for the time limit was chosen to be sufficiently large to allow for at least one successful dispersal between those landscape elements for which the longest field dispersal had been recorded. Initially, a user-defined gap tolerance level is set. Gap tolerance refers to the maximum distance without vegetation cover that a particular species might cross during dispersal. This concept relies on an underlying assumption of the model that the species in question prefers the cover of native vegetation during dispersal, but will, to some extent, cross open country if necessary. A simplified sequence of events is as follows:

   1) the initial direction of travel (north, south, east, or west) is chosen randomly;

   2) of the three available grid cells in the chosen direction (left front, front, right front), that with the highest vegetation quality (breeding habitat > dense native vegetation > sparse native vegetation) is chosen as the next step, provided that it is not agricultural land;

   3) if two or more cells have equal value, the next step is chosen randomly;

   4) if all three cells are agricultural land, d randomly turns right or left and proceeds as in step (2) with a revised general direction;

   5) if d is still unable to move after inspecting right and left options, the horizon is scanned for native vegetation in an arc extending in front of d for as far as the designated gap tolerance level. Once native vegetation is detected, d moves directly to it;

   6) if d is still unable to move after inspecting the horizon ahead and to left and right, it may retrace its steps;

   7) after each move, d is given a 25% chance of randomly altering direction. The 25% level was chosen after trial and error to provide a satisfactory movement algorithm for d that would allow it to fully explore any available vegetation, without becoming caught in a cul-de-sac, always taking the same route, or going round in circles;

   8) each iteration continues until either the target is reached or d has moved 10 000 steps;

   9) after 100 iterations for any particular patch pair, the following results are recorded: number of successful dispersals (number of times that d found the target), termed simulated dispersal frequencies; the median distance traveled during successful dispersals, termed simulated corridor distances; and the straight-line distances between patch pairs (i.e., between pseudo-centroids or arbitrary points centrally located within each patch). For ease of computation, distances (number of 30-m steps) are converted to simulation units, in which one step equals 0.03 simulation units. Note that simulated dispersal frequencies can be obtained for every patch pair involved in a simulation, with values ranging from 0 to 100, whereas simulated corridor distances can be obtained only for patch pairs with simulated dispersal frequencies > 0.

At landscape boundaries, d disappears. In theory, this should result in a decreased likelihood of reaching the destination. In practice, however, it did not, as care was taken to make each landscape sufficiently large so that dispersal origins did not occur close to boundaries. Consequently, any disperser that reached a boundary was close to the end of its "time" limit, which meant that behavior at boundaries was inconsequential.

When gap tolerance is set at infinity, d moves as before, except that, when unable to proceed through native vegetation (see step 5), it can move randomly through agricultural land until a scan of the horizon (set at 270 m) reveals native vegetation. Thus, the simulated dispersal frequencies obtained at this setting describe the case in which movement through all landscape elements is essentially random, except that native vegetation is preferred over agricultural land if there is a choice. In the real world, this might correspond to a habitat-specific animal that is not inhibited by the size of a corridor gap.

When the gap tolerance setting is null, d moves randomly through both native vegetation and agricultural land indiscriminately. In the real world, this might correspond to an animal that shows no preference for native vegetation and, hence, does not use corridor routes.

Assumptions and rationale of the model

Apart from the infinite and null settings, the model is based on the assumption that a habitat-specific animal will disperse randomly through corridors of vegetation, in preference to open agricultural or pastoral land, while crossing gaps up to some maximum width that is a species-specific characteristic. Hence, the likelihood of d moving from one patch to another depends on (1) corridor continuity (size of gaps), (2) corridor distance, and (3) corridor complexity (i.e., degree of branching). Gaps that are too wide for the species to cross will prevent dispersal to some destinations and alter the likelihood of dispersal to others by forcing the use of alternate routes. With increasing distance, d will be less likely to find a given destination within the time limit. This corresponds to the real world situation in which a nearby disperser is more likely to obtain a vacancy than is a more distant disperser, as the former will reach the vacancy first. With increasing corridor complexity, d will have more alternative directional choices and, hence, will be likely to travel greater distances.

Theoretical example

To demonstrate the working of the model, we present a simple experimental landscape configuration (Fig. 4), incorporating four gap widths (60 m, 90 m, 120 m, and 150 m) and four corridor distances between dispersal origin (A) and target destinations (B, C, D, ... I). If we assume that the species in question has a 90-m gap tolerance, we can predict that a disperser leaving A will be likely to reach B, C, D, and E because the the gaps between these patch pairs are less than or equal to the species gap tolerance, but will be unable to reach F, G, H, or I because corridor gaps > 90 m will prevent this. Further, we predict that the likelihood of reaching A, B, C, and D will be inversely proportional to the corridor distances between these patch pairs.

Fig. 4. Diagram of the experimental landscape configuration showing four gap widths (60-, 90-, 120-, and 150-m) and a range of corridor distances between the dispersal origin (A) and destinations (B, C, D... I).

A run of the simulation model on the experimental landscape, with gap tolerance set at 90 m, produced a set of simulation results in accord with our predictions (Table 1). Note that the simulated corridor distances are two orders of magnitude larger than the straight-line distances, due to the random movement algorithm whereby d rarely continues in the same direction for any length of time and, consequently, traces a meandering exploratory pathway rather than a minimum corridor route. Note also that, in this example and in many real landscapes, corridor routes tend to become more complex (i.e., possess more directional choices) with increased distance.

Real dispersal frequencies were gathered in the field from study populations of the Blue-breasted Fairy-wren Malurus pulcherrimus (Brooker and Brooker 1997) and the White-browed Babbler Pomatostomus superciliosus (P. Cale, unpublished data) occupying remnant patches of native vegetation among crops and bare paddocks to the north of Kellerberrin, Western Australia (Fig. 1). As part of more extensive population studies, adults and fledglings of these species were fitted with individually recognizable color combinations of plastic leg bands.

Blue-breasted Fairy-wrens are relatively sedentary, habitat-specific, cooperative-breeding birds that live in family groups of 2 - 7 adults. These groups occupy year-round breeding and feeding territories and offspring usually remain with their natal group for at least 6 to 12 mo. Many of the offspring disperse at one year of age, whereas others remain with the natal group as adult helpers, some dispersing at two or more years old, and others never dispersing. White-browed Babblers are also habitat-specific, cooperative-breeding birds. During the breeding season, groups of 2 - 13 adults occupy exclusive territories, the boundaries of which are relaxed into overlapping home ranges during the nonbreeding period. Offspring remain within the natal territory for at least 12 mo. Some birds disperse after 12 mo, but others can remain in their natal territory for several years before dispersing, whereas others never disperse. At the start of each breeding season (1994-1997 for wrens, 1995-1997 for babblers), permanent dispersals of banded birds were recorded. A permanent dispersal was defined as one in which the disperser remained with its destination group for at least one breeding season. For Blue-breasted Fairy-wrens, all dispersals were to breeding vacancies. For White-browed Babblers, some dispersals were to breeding vacancies, whereas many others involved the movement of helpers to groups in which they continued to act as helpers (P. Cale, personal observation).

For each species, a database was developed to itemize for each patch pair (i.e., group of dispersal origin and destination group) the number of individuals that moved from A to B in a given breeding season (termed dispersals), and the number of vacancies to which these individuals could have dispersed (termed dispersal opportunities). For Blue-breasted Fairy-wrens, a dispersal opportunity for a given sex in a given year was defined as a group into which a disperser had moved (see Fig. 5 for diagrammatic explanation). Note that, although other opportunities may have been available to dispersing wrens, those just defined were the only ones that we could be certain of and, hence, were the only ones suitable for modeling purposes. For White-browed Babblers, a dispersal opportunity in any given year was considered to be a group into which a disperser had moved, regardless of which sex it may have been. Wrens and babblers were treated differently in this respect, as the latter are behaviorally more flexible when joining new groups, in that the presence of a breeding vacancy is not required (P. Cale, personal observation).

Fig. 5. Diagrammatic representation of six territories (A, B, C, D, E, and F), showing two dispersals (solid lines) and four dispersal opportunities (solid and dotted lines). A and C are termed dispersal origins and B and D are destinations (vacancies). B and D are defined as vacancies because dispersers moved into them from elsewhere. Note that territories E and F, although present in the population, would not be involved in the simulation because they contain neither dispersers nor vacancies, nor potential dispersers subsequently lost.

For Blue-breasted Fairy-wrens, M. and L. Brooker recorded 71 dispersals from a total of 750 dispersal opportunities among 599 patch pairs. An additional 37 potential dispersers survived to the start of the breeding season, but were never seen again. For White-browed Babblers, P. Cale recorded 36 dispersals from a total of 333 dispersal opportunities among 214 patch pairs. An additional 11 potential dispersers survived to the start of the breeding season, but were never seen again. As each breeding group in each study was monitored exhaustively throughout each breeding season, we are confident that the lost birds either died during dispersal or dispersed outside the respective study areas.

Simulation results were related to real dispersal frequencies using logistic regression models (computer package GLIM; Baker and Nelder 1978) in which the error structure is assumed to be binomial and the data are logit transformed. In each case, the number of real dispersals was treated as the y- variate, with the number of dispersal opportunities as the binomial denominator. The standard output from fitting a GLIM model is the residual deviance, which for the normal distribution is the residual sum of squares; hence, the smaller the residual deviance, the better the model fit (Aitkin et al. 1990). Other analyses involved simple linear regression, assuming a normal error structure.

Quantifying corridor use

Dispersal simulations performed at different gap tolerance levels provided multiple sets of simulated dispersal frequencies and median simulated corridor distances for comparison with real dispersal frequencies. The various sets of simulation results differ from one another, because the smaller the gap tolerance, the less likely that d can reach every target. Even when a target can be reached, different levels of gap tolerance affect which routes can be taken and, hence, affect simulated distances.

In our theoretical example, we assumed that the study species had a 90-m gap tolerance level. In the real world, however, gap tolerance is rarely known with accuracy. Therefore, our first aim in analyzing the data was to use the various sets of simulation results, performed at different levels of gap tolerance, to determine which set most closely matched the observed dispersal frequencies of the birds, thus allowing us to determine their gap tolerance.

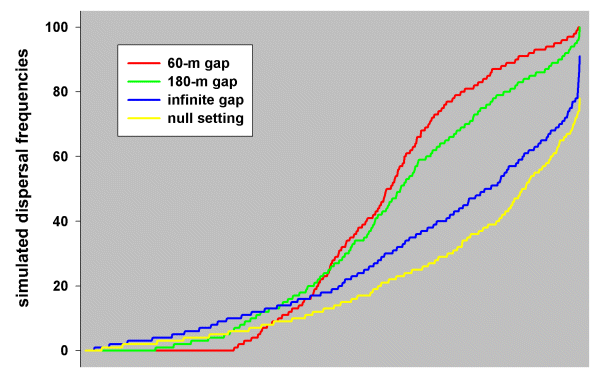
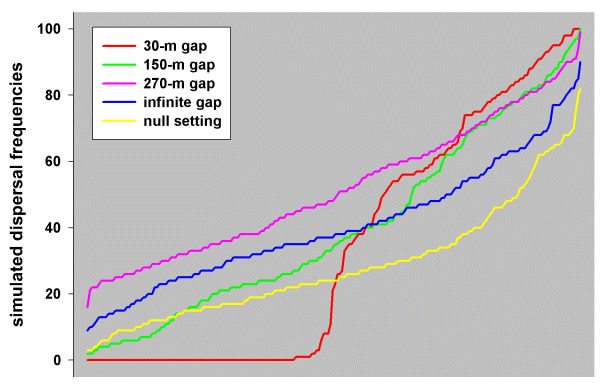
Prior to the analysis, we had expected that the gap tolerance of Blue-breasted Fairy-wrens would be < 100 m. This was based on behavioral observations: wrens were never observed flying across open paddocks between patches of native vegetation; even within their own territories, they tended to move from bush to bush, avoiding open flight; the longest open flight that we observed was within a home territory across about 90 m of wheatfield to a small stand of acacia trees. We therefore ran multiple simulations at 30-, 60-, 90-, 120-, 150-, and 180-m gap levels, as well as at infinite and null settings, on the Blue-breasted Fairy-wren study landscape, from which we obtained eight sets of simulation results. At the 60-m gap level, many patch pairs (those effectively isolated by > 60-m gaps) were without any dispersal success, whereas others (those connected by vegetation corridors with 60-m gaps or smaller) received up to 100% dispersals (see red profile in Fig. 6). As gap levels increased, the shape of the profiles changed until at the infinite gap setting and the null setting, only one or two patch pairs (those most distant from the origin) were without dispersal success, whereas none experienced 100% success (blue and yellow profiles, respectively, in Fig. 6). This was because both the infinite gap and random movement (null) hypotheses always give a disperser some chance of traveling in the wrong direction, whereas being confined to a corridor might have always directed a disperser toward a target.

Fig. 6. Profiles of simulated dispersal frequencies generated by the simulation model set at 60-m gap, 180-m gap, infinite gap, and null settings, run on the Blue-breasted Fairy-wren study landscape (each set of frequencies is plotted in ascending order).

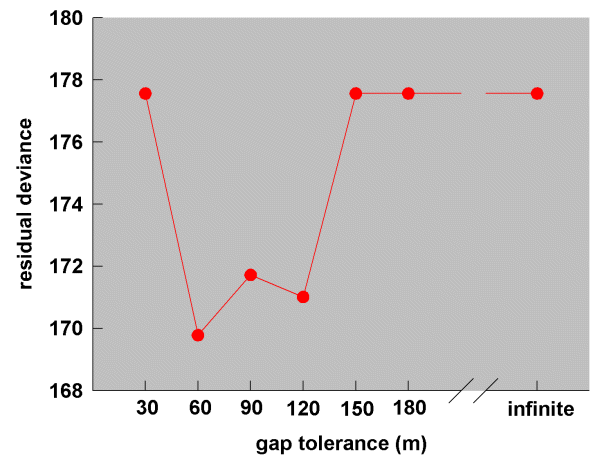
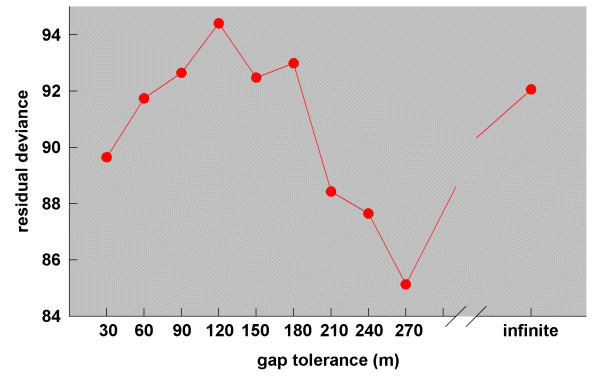
In order to determine which set of simulation results best fitted the real dispersal data, we built, for each set of simulation results, a logistic regression model (see section Data analysis) in which the real dispersal frequencies from the study population (treated as the y- variate with number of dispersal opportunities as the binomial demoninator) were regressed against the simulated dispersal frequencies. In each case, we omitted those data involving dispersals within the same vegetation remnant (i.e., between contiguous territories where no corridor was involved), using only dispersals between different vegetation remnants. A comparison of the residual deviances from the eight gap models tracked a roughly concave parabola (30 - 180 m and infinite, shown in Fig. 7), indicating that there was an optimum level of gap tolerance at which the simulation results best matched the real data. Note that, if the wrens had not used corridor routes, we would have expected either the infinite or the null models to have had the smallest residual deviance. In fact, the smallest residual deviance was at the 60-m gap level, whereas there was no significant change in deviance for either the infinite or the null model (60 m, change in deviance 7.82, df = 1, P < 0.01; infinite gap, change in deviance 2.62, df = 1, n.s.; null setting, change in deviance 2.50, df = 1, n.s.). We therefore conclude that Blue-breasted Fairy-wrens in the study population indeed used corridor routes during dispersal and, in doing so, were inhibited by gaps > 60 m.

Fig. 7. Residual deviances from seven logistic regression models relating simulation results run at seven different gap tolerance levels to the observed dispersal frequencies of Blue-breasted Fairy-wrens. For the 30-, 150-, 180-m, and infinite regression models (and also for model, not shown here), there was no significant change in deviance. Hence, the plotted values represent total deviances.

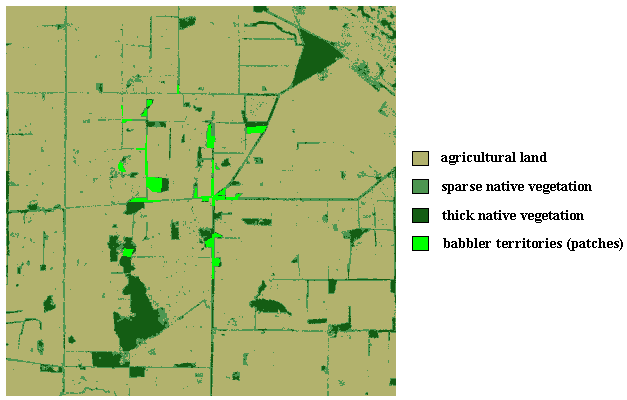
Prior to analysis, we had expected that White-browed Babblers would have a much larger gap tolerance than wrens. Babblers are larger than wrens (40 g vs. 8 g), are more often observed in the open, and tend to fly for longer distances across open areas; nevertheless, like wrens, they prefer to move from bush to bush rather than cross open gaps in vegetation. Thus, we ran multiple simulations on the White-browed Babbler study landscape (Fig. 8) at 30-, 60-, 90-, 120- 150-, 180-, 210-, 240-, and 270-m and infinite gaps and at null settings (see Fig. 9 for examples of frequencies profiles).

Fig. 8. Color-coded representation of White-browed Babbler study landscape showing relative locations of babbler territories (patches) used in the simulations.

Fig. 9. Profiles of simulated dispersal frequencies generated by the simulation model set at 30-m gap, 150-m gap, 270-m gap, infinite gap, and null settings, run on the White-browed Babbler study landscape (each set of frequencies is plotted in ascending order).

Comparison of the residual deviances from the 11 logistic regression models relating simulation results to the observed dispersal frequencies (Fig. 10) suggests that, on average, White-browed Babblers in the study landscape were willing to cross gaps at least 270 m wide. Nevertheless, movement across paddocks was not random, as would have been indicated by relatively small residual deviances for the infinite gap and/or null models (270 m, change in deviance 18.56, df = 1, P < 0.001; infinite gap, change in deviance 11.62, df = 1, P < 0.001; null setting, change in deviance 15.34, df = 1, P < 0.001).

Fig. 10. Residual deviances from 10 logistic regression models relating simulation results run at 10 different gap tolerance levels to the observed dispersal frequencies of White-browed Babblers (the null model is not shown; residual deviance is 88.35).

Estimating dispersal mortality rate

In order to obtain a measure of dispersal mortality per unit distance traveled, we compared the likelihood of successful dispersal between patch pairs for survivors (i.e., birds suffering no dispersal mortality) with the likelihood of successful dispersal for all birds (i.e., birds presumably suffering some degree of dispersal mortality). Because both of these probability estimates take into account the likelihood of dispersal elsewhere (to other patches in or outside the study area), the difference between them can be due only to dispersal mortality. When this difference (i.e., the mortality risk) is related to simulated corridor distances, the relationship gives a model-dependent but landscape-independent measure of dispersal mortality per unit distance traveled. As far as we are aware, this is the first time that dispersal mortality with respect to distance traveled has been partitioned from the likelihood of outside dispersal.

Accepting that Blue-breasted Fairy-wrens used corridor routes with a gap tolerance of around 60 m, we used the simulation results obtained from the 60-m gap tolerance run to calculate mortality risk by first estimating the chance of successful dispersal in the absence of dispersal mortality (Model 1) and then the chance of successful dispersal given some unknown rate of dispersal mortality (Model 2) (Table 2). We calculated mortality risk as (e₁ - e₂) / e_1, where e₁ is the estimate from Model 1 and e₂ is the estimate from Model 2. In effect, this represents the birds that died during dispersal as a proportion of those that might otherwise have been expected to reach their destination.

We estimated the chance of successful dispersal in the absence of mortality (Model 1), using a logistic regression model with real dispersers as the y- variate and the dispersal opportunities available to them as the binomial denominator (as before), using patch pairs both within and between vegetation remnants. We know that there was no dispersal mortality among these birds because they all reached their destinations. We estimated the chance of successful dispersal, given some unkown rate of mortality (Model 2), using a logistic regression model with real dispersals as the y- variate and, this time as the denominator, the number of dispersal opportunities available to all birds (i.e., dispersers plus birds that were present at the start of the dispersal period but were never seen again).

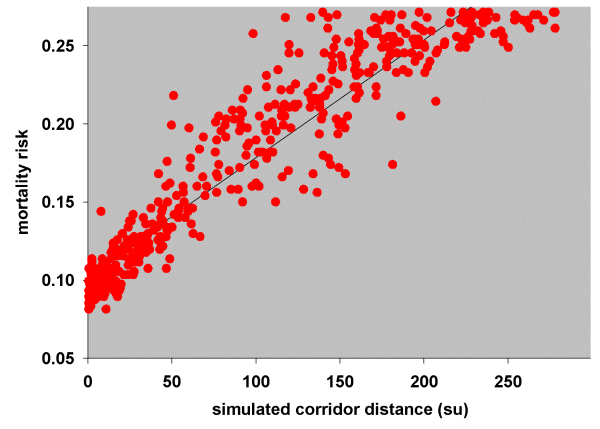
The risk of death, (e₁ - e₂)/e_1, was then plotted as a function of the simulated corridor distances (Fig. 11). Patch pairs with a simulated dispersal frequency of zero were omitted from this plot, firstly because there were no distance measurements for these points (see Simulation model) and secondly, because patch pairs with very low dispersal probabilities can have had little bearing on mortality rates. A simple linear regression suggests that 0.00075 wrens per simulation unit died during dispersal.

Fig. 11. Relationship between mortality risk and simulated corridor distances (su, simulation units) for Blue-breasted Fairy-wrens.

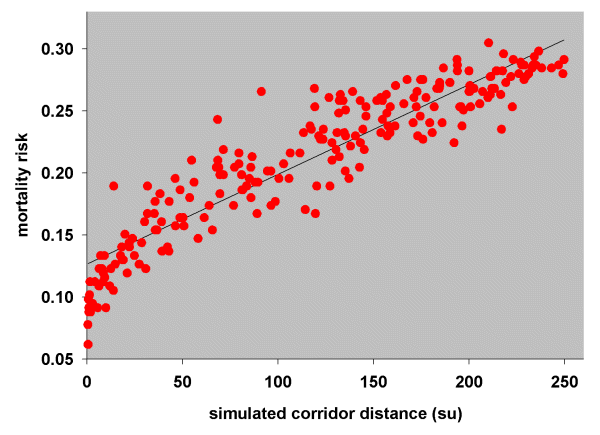
Using the same methodology for White-browed Babblers and using simulation results from the 270-m gap tolerance run, we estimated the chance of successful dispersal for surviving babblers (Model 1, Table 3) and all babblers (Model 2, Table 3) and calculated their mortality risk. Simple linear regression of mortality risk on simulated corridor distances (Fig. 12) suggests that 0.00072 babblers per simulation unit died during dispersal. Note that this figure is almost the same as the mortality rate calculated for Blue-breasted Fairy-wrens.

Fig. 12. Relationship between mortality risk and simulated corridor distances (su, simulation units) for White-browed Babblers.

Because we have effectively partitioned the risk of mortality from the chance of outside dispersal, and because our estimates of dispersal mortality are model dependent but landscape independent, they can be transported to other landscapes on which simulations have been run. Thus, they can be used in population viability assessment of unstudied or hypothetical animal populations. Where corridor-dependent species are concerned, mortality rates based on straight-line distances cannot be used in this way, as the estimate will be landscape specific.

Comparing dispersal qualities of landscapes

The simulation results can be used in a number of different way to assess and compare the dispersal qualities of landscapes. Such procedures could be used by land planners and land managers wishing to assess the suitability of particular landscapes for species reintroductions, or for making changes to a landscape that might improve the persistence likelihood of particular species or for evaluating revegetation proposals.

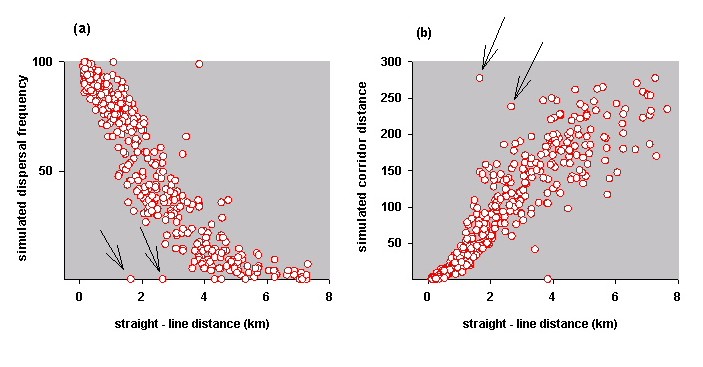
For example, by plotting the simulation results against straight-line distances, it is easy to identify those patch pairs that are the least well connected and, therefore, perhaps most in need of restoration or revegetation. The arrows in Fig. 13a indicate patch pairs in the Blue-breasted Fairy-wren study area that are relatively close, yet inaccessible to wrens, according to the model. The arrows in Fig. 13b indicate patch pairs with long simulated corridor distances relative to straight-line distances, where strategic planning for shorter corridor routes might be advantageous.

Fig. 13. Relationship between simulation results and straight-line distances for patch pairs in the Blue-breasted Fairy-wren study landscape. Each plot indicates locations where strategic planning for new or shorter corridors might be advantageous. (a) Simulated dispersal frequencies relative to straight-line line distances. Arrows indicate two patch pairs that have a small chance of successful dispersal according to the model, yet are geographically close to one another. (b) Simulated corridor distances relative to straight-line distances. Arrows indicate two patch pairs with long simulated distances relative to straight-line distances.

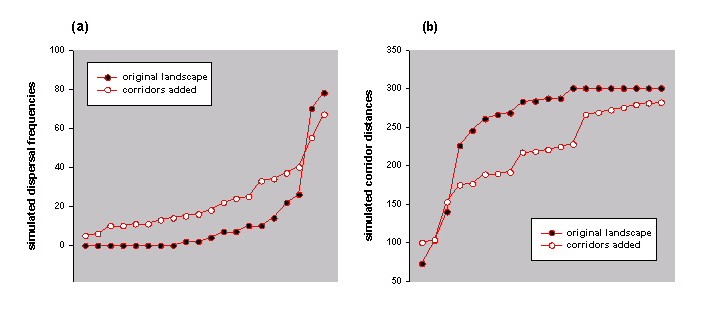
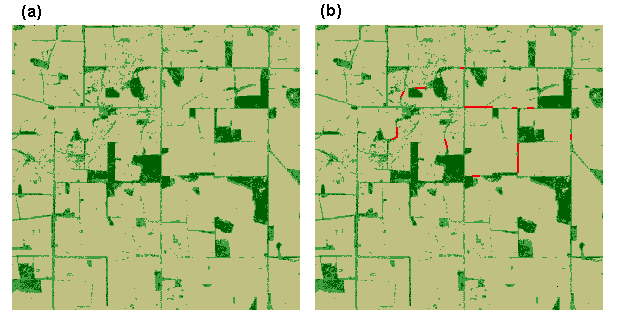
Similarly, comparative profiles of simulated dispersal frequencies and simulated corridor distances could be used to compare alternative landscape scenarios. Fig. 14 shows the same landscape before and after proposed corridor restoration, together with the respective simulation results (Fig. 15). It can be seen that the proposed restoration would, in theory, increase the likelihood of successful dispersal between patches and decrease the median distances traveled by successful dispersers.

Fig. 14. Landscape without (a) and with (b) proposed vegetation corridors (in red).

Fig. 15. (a) Simulated dispersal frequencies before and after proposed corridor restoration (each set of frequencies is plotted in ascending order). (b) Median simulated distances before and after proposed corridor restoration (each set of distances is plotted in ascending order).

For endangered species that are typically restricted in their dispersal range and in the kinds of habitat through which they can disperse, factors such as spatial configuration of the landscape and species-specific dispersal behaviors are of primary importance (Fahrig and Merriam 1994). For this reason, answers to practical conservation questions can come only from studies of real populations in real landscapes (Hobbs 1992), although there is a need to couple empirical studies with theoretical models in the proper investigation of the consequences of spatial heterogeneity (Johnson et al. 1992, Tischendorf and Wissel 1997).

Although we do not pretend that our simulations provide a very "good" model of the real dispersal frequencies recorded in this study (for example, the Blue-breasted Fairy-wren statistical Model 1 in Table 2 explained only 10% of the total deviance in dispersal frequencies), there are myriad environmental and behavioral reasons why this should be so. First and foremost, individuals obviously do not travel in a purely random way, even if they confine themselves to corridors; directional choices may be affected by prior knowledge of the landscape, by traveling companions, by conspecific attraction, or by ephemeral changes in the matrix (although for conservation purposes, our minimalist assumption of "no cover in agricultural land" is the safest). Once a disperser has reached a vacancy, the decision whether or not to take it may depend on something as unpredictable as whether or not the disperser finds the potential mate attractive, or whether the disperser is related to the potential mate. Nevertheless, our simulations provided data that were sufficiently "good" to tell us what we needed to know: that both Blue-breasted Fairy-wrens and White-browed Babblers used vegetation corridors during dispersal. Blue-breasted Fairy-wrens had a gap tolerance level of no more than about 60 m, whereas White-browed Babblers crossed open gaps at least 270 m wide.

From a theoretical viewpoint, our finding similar rates of dispersal mortality in Blue-breasted Fairy-wrens and White-browed Babblers makes sense if species have evolved behaviors (gap tolerances) that minimize dispersal mortality. Yet, what this means is that species with small gap tolerances, such as the Blue-breasted Fairy-wren, must depend on suitably connected corridors of vegetation for population persistence. Our model therefore provides a means of identifying dispersal-limited species. This ability is an important facet of procedures aimed at conserving biodiversity. For example, in one such proposal involving focal or umbrella species, it has been suggested that if a landscape meets the needs of species with, perhaps, low gap tolerance levels (i.e., dispersal-limited species), it will also encapsulate the needs of a suite of less demanding species (i.e., those with higher gap tolerance levels) (Lambeck 1997). However, this procedure relies on the ability to correctly identify the focal species. In future work, we hope to use the simulation model to undertake a more general comparative study to identify more corridor dependent species and to examine further the relationship between dispersal mortality and gap tolerance levels.

Responses to this article are invited. If accepted for publication, your response will be hyperlinked to the article. To submit a comment, follow this link. To read comments already accepted, follow this link.

We wish to thank the farmers and landowners of the Kellerberrin, Wyalkatchem, and Trayning areas for permission to conduct our research within their preserved areas of native vegetation. We enjoyed stimulating discussions with Graeme Smith, who with Robert Lambeck and Gary Luck also provided most helpful comments on earlier drafts of the paper. Graeme Chapman provided photographs of the study species.

Aitkin, M., D. Anderson, B. Francis, and J. Hinde. 1990. Statistical modelling in GLIM. Clarendon Press, Oxford, UK.

Andreassen, H. P., S. Halle, and R. A. Ims. 1996a. Optimal width of movement corridors for root voles: not too narrow and not too wide. Journal of Applied Ecology 33: 63-70.

Andreassen, H. P., R. A. Ims, and O. K. Steinset. 1996b. Discontinuous habitat corridors: effects on male root vole movements. Journal of Applied Ecology 33: 555-560.

Arnold, G. W., J. R. Weeldenburg, and D. E. Steven. 1991. Distribution and abundance of two species of kangaroo in remnants of native vegetation in the central wheatbelt of Western Australia and the role of native vegetation along road verges and fencelines as linkages. Pages 273-280 in D. A. Saunders and R. J. Hobbs, editors. Nature conservation 2: the role of corridors. Surrey Beatty, Sydney, Australia.

Baker, R. J., and J. A. Nelder. 1978. The GLIM system. Royal Statistical Society, Oxford, UK.

Bentley, J. M., and C. P. Catterall. 1997. The use of bushland, corridors and linear remnants by birds in southeastern Queensland, Australia. Conservation Biology 11: 1173-1189.

Brooker, M., and L. Brooker. 1997. Dispersal of the Blue-breasted Fairy-wren in fragmented habitat in the wheatbelt of Western Australia. Pacific Conservation Biology 3: 295-300.

Brooker, M., and C. R. Margules. 1996. The relative conservation value of remnant patches of native vegetation in the wheatbelt of Western Australia: I. Plant diversity. Pacific Conservation Biology 2: 268-278.

Cale, P. 1990. The value of road reserves to the avifauna of the central wheatbelt of Western Australia. Proceedings of the Ecological Society of Australia 16: 359-367.

Desrochers, A., and S. J. Hannon. 1997. Gap crossing decisions by forest songbirds during the post-fledging period. Conservation Biology 11: 1204-1210.

Fahrig, L., and G. Merriam. 1994. Conservation of fragmented populations. Conservation Biology 8: 50-59.

Hinsley, S. A., P. E. Bellamy, I. Newton, and T. H. Sparks. 1995. Habitat and landscape factors influencing the presence of individual breeding bird species in woodland fragments. Journal of Avian Biology 26: 94-104.

Hobbs, R. J. 1992. The role of corridors: solution or bandwagon? Trends in Ecology and Evolution 7: 389-392.

Johnson, A. R., J. A. Weins, B. T. Milne, and T. O. Crist. 1992. Animal movements and population dynamics in heterogeneous landscapes. Landscape Ecology 7: 63-75.

Lambeck, R. J. 1997. Focal species: a multi-species umbrella for nature conservation. Conservation Biology 11: 849-856.

Lindenmayer, D. B., R. B. Cunningham, C. F. Donnelly, B. J. Triggs, and M. Belvedere. 1994. The conservation of arboreal marsupials in the montane ash forests of the central highlands of Victoria, south-eastern Australia. V. Patterns of use and the microhabitat requirements of the mountain brushtail possum Trichosurus caninus Ogilby in retained linear habitats (wildlife corridors). Biological Conservation 68: 43-51.

Lynch, J. F., and D. A. Saunders. 1991. Responses of bird species to habitat fragmentation in the wheatbelt of Western Australia: interiors, edges and corridors. Pages 143-158 in D. A. Saunders and R. J. Hobbs, editors. Nature conservation 2: the role of corridors. Surrey Beatty, Sydney, Australia.

Rail, J. F., M. Darveau, A. Desrochers, and J. Huot. 1997. Territorial responses of boreal forest birds to habitat gaps. Condor 99: 976-980.

Ruckelshaus, M., C. Hartway, and P. Kareiva. 1997. Assessing the data requirements of spatially explicit dispersal models. Conservation Biology 11: 1298-1306.

Ruefenacht, B., and R. L. Knight. 1995. Influences of corridor cntinuity and width on survival and movement of deermice Peromyscus maniculatus. Biological Conservation 71: 269-274.

Sarre, S., K. Wiegand, and K. Henle. 1996. The conservation biology of a specialist and a generalist gecko in the fragmented landscape of the Western Australian wheatbelt. Pages 39-51 in J. Settele, C. Margules, P. Poschlod, and K. Henle, editors. Species survival in fragmented landscapes. Kluwer Academic Publishers, London, UK.

Saunders, D. A., and C. P. de Rebeira. 1991. Values of corridors to avian populations in a fragmented landscape. Pages 221-240 in D. A. Saunders and R. J. Hobbs, editors. Nature conservation 2: the role of corridors. Surrey Beatty, Sydney, Australia.

Schippers, P., J. Verboom, J. P. Knaapen, and R. C. van Apeldoorn. 1996. Dispersal and habitat connectivity in complex heterogeneous landscapes: an analysis with a GIS-based random walk model. Ecography 19: 97-106.

Tischendorf, L., and C. Wissel. 1997. Corridors as conduits for small animals: attainable distances depending on movement pattern, boundary reaction and corridor width. Oikos 79: 603-611.

Appendix 1. Windows self-extracting zip file containing executable file (seds.exe) and associated image and text files necessary to run a demonstration of the simulation model (only suitable for IBM compatible computers with VGA color monitor or similar, preferably with Pentium processor, running Windows software). Download append1.exe to your computer. When you run append1.exe, the program files will install themselves in c:\demo directory or a directory that you nominate. After installation, simply run c:\demo\seds.exe and follow the instructions (see also readme.txt).

Appendix 2. Technical details: GIS, aerial photo mosaics, and computer code.

Aerial photo mosaics

The landscape images used in the simulation model were produced on a raster-based GIS (Idrisi, Clark University, MA) from a digital air photo mosaic made from 1: 25 000 aerial photos taken in 1994, provided by the Western Australian Department of Land Administration. Aerial photos were used in preference to Landsat TM images, because the initial resolution of a Landsat TM image is too coarse to accurately define small vegetation elements that may be important to dispersing animals (e.g., individual shrubs and trees). For the Blue-breasted Fairy-wren study landscape, (23 000 ha) we used 28 aerial photos to produce the mosaic; for the White-browed Babbler landscape (14 000 ha), 21 were needed.

Because no two consecutive aerial photos are taken from exactly the same angle, they are subject to individual distortion. To rectify this problem, we used a rubber-sheet transformation (first-order polynomial fit, nearest neighbor resampling) to register each image against a Landsat TM scene of the entire study area. (If a Landsat scene is not available, any digital representation of the entire area would be suitable). An aerial photo mosaic was then produced at 5- m resolution (i.e., each pixel depicts a 5-m square).

The final landscape image was produced by reclassifying individual pixel values of the mosaic into one of two categories: vegetation and other. This 5-m image was then contracted by pixel aggregation to a 30-m image and the pixel values were further reclassified into agricultural land (no 5-m pixels with vegetation per 30-m pixel), sparse vegetation (1-18 5-m pixels with vegetation per 30-m pixel), and thick vegetation (19-36 5-m pixels with vegetation per 30-m pixel).

Separate images (of the same 30-m resolution and overall dimensions) representing the bird territories (patches) and their psuedo-centroids (points centrally located within each patch) were digitized by hand, using the landscape image as a backdrop.

All image files were saved as raw single-byte binary files with no file header.

Computer code

The simulation software was written in C programming language as a stand-alone executable file for IBM-compatible computers. The advantage of this approach is that the software can access raw image files made using any raster-based GIS software and is therefore not platform specific.