|
|
|
Copyright ©1999 by The Resilience Alliance*
Dunham, J., M. Peacock, C. R. Tracy, J. Nielsen, and G. Vinyard. 1999. Assessing extinction risk: integrating genetic information. Conservation Ecology [online] 3(1): 2. Available from the Internet. URL: http://www.consecol.org/vol3/iss1/art2/
A version of this article in which text, figures, tables, and appendices are separate files may be found by following this link.
Insight Assessing Extinction Risk: Integrating Genetic Information Jason Dunham1, Mary Peacock1, C. Richard Tracy1, Jennifer Nielsen2, and Gary Vinyard1
1University of Nevada-Reno; 2Stanford University
- Abstract
- Introduction
- Genetic Information and Assessing Extinction Risk
- Caveats and Conclusions
- Responses to this Article
- Acknowledgments
- Literature Cited
Risks of population extinction have been estimated using a variety of methods incorporating information from different spatial and temporal scales. We briefly consider how several broad classes of extinction risk assessments, including population viability analysis, incidence functions, and ranking methods integrate information on different temporal and spatial scales. In many circumstances, data from surveys of neutral genetic variability within, and among, populations can provide information useful for assessing extinction risk. Patterns of genetic variability resulting from past and present ecological and demographic events, can indicate risks of extinction that are otherwise difficult to infer from ecological and demographic analyses alone. We provide examples of how patterns of neutral genetic variability, both within, and among populations, can be used to corroborate and complement extinction risk assessments.
KEY WORDS: extinction risk, genetic variation, incidence function analysis, population viability analysis, ranking methods, risk assessment, spatial scale, temporal scale.
Published February 16, 1999.
Assessment of extinction risk among populations is one of the central problems of conservation biology. The development of reliable, yet practical, methods to assess extinction risk is an active and controversial area of investigation (Simberloff 1988, Mace and Lande 1991, Boyce 1992, Burgman et al. 1993, Caughley 1994, Taylor 1995, Mills et al. 1996). Extinction risk is typically assessed in terms of ecological and demographic risk factors (Caughley 1994). Data-intensive methods such as population viability analysis (Gilpin and Soulé 1986, Boyce 1992, Beissinger and Westphal 1998) can be useful when extinction risk of only one or a few populations is in question. When species consist of many populations that may be declining on a local or regional basis, the extinction risk of many local populations must be considered. In such cases, assessments of extinction risk may be obtained by quantitative methods, such as incidence-function analysis (Hanski 1997), or by qualitative ranking methods that incorporate varying types of information (Mace and Lande 1991, Given and Norton 1993, Allendorf et al. 1997). Each method incorporates information on different temporal and spatial scales, and may give potentially different, but complementary, answers to the question of extinction risk (Table 1).
Table 1. Comparison of information from population viability analysis, incidence functions, ranking methods, and genetics.
|
Unfortunately, the only objective way to check the validity of extinction risk estimates is to postpone conservation actions and allow more populations to actually go extinct, clearly an unpopular option for imperiled species. Consequently, estimates of extinction risk may be difficult to establish or validate. Comparison of extinction risk estimates from alternative models or methods of assessment can identify important areas of disagreement and for future research, however (Beissinger and Westphal 1998).
In this essay, we briefly consider the potential for patterns of variability in neutral genetic markers to serve as indicators of extinction risk. Although linkages between extinction risk and genetic variability may be obvious to population biologists, opportunities for management applications are only beginning to be fully realized. Our goal in this essay is to focus more attention on the potential utility of genetic variation to serve as a symptom, rather than a cause, of extinction risk (e.g., Caro and Laurenson 1994, Frankham 1995, Lande 1995, Hedrick et al. 1996). A growing literature on the possibilities of linking genetics and ecology in conservation biology (Hastings and Harrison 1994, Milligan et al. 1994, Moritz 1994) suggests that this may be a fruitful approach.
Genetic analysis of population structure typically involves estimating the amount and distribution of genetic variation within and among populations. There are several lines of evidence suggesting that patterns of genetic variation, both within and among populations, may be related to the extinction risk of populations.
Patterns of genetic variation may have a very strong historical component (Slatkin 1985) and, thus, may be a product of very long-term processes. Under many conditions, the effects of historical events can persist for many generations (Avise et al. 1987, Boileau et al. 1992). Historical processes that may decrease genetic variation within populations and increase variation among populations include drift, in small populations, and founder and bottleneck effects (Nei et al. 1975, Boileau et al. 1992, Leberg 1992, DeMarais et al. 1993, Frankham 1996, Richards and Leberg 1996). Extinction-recolonization dynamics also may decrease differentiation within and among local populations, particularly when population turnover rates are high (Hedrick 1996, Hedrick and Gilpin 1996).
This linkage between population size and variability and genetic variation suggests that levels of within- and among-population variability may reflect the relative risk of extinction among populations (Fig. 1). In theory, extinction risk may be inversely related to population size and positively related to variability in population size (e.g., Shaffer 1981, Goodman 1987, Lande 1993; see Fig. 1). This relationship has been suggested for some empirical data, but generalization of this pattern remains controversial (see Pimm et al. 1988, Schoener and Spiller 1992, Tracy and George 1992) and should be regarded as a working hypothesis.
If our characterization of relationships between genetic variation and extinction risk is correct (Fig. 1), then levels of within-population genetic variation and estimates of extinction risk may be inversely related. A recent review of patterns of within-population variability across a wide range of taxa (Frankham 1996) supports this generalization. Frankham found direct correlations between levels of within-population genetic variation and measures of population size, and significantly lower levels of genetic variation in endangered vs. nonendangered species.
At the among-population scale, recent empirical study of a butterfly metapopulation (Saccheri et al. 1998) similarly found a direct correlation between the extinction risk of local populations and heterozygosity. Saccheri et al. also provided circumstantial evidence to implicate inbreeding in populations with reduced heterozygosity as a mechanism contributing to local extinctions. In this example, reduced genetic variability may be a symptom, as well as a cause, of local extinctions.
Certainly, discrepancies from hypothesized patterns in Fig. 1 are expected. Such discrepancies may reveal instances in which demographic or ecological events have not been appropriately incorporated into assessments of extinction risk, or cases in which genetic variability is a poor indicator of risk (see Caveats and conclusions). Examples of potential discrepancies will be described.
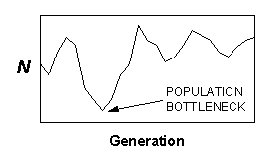
First, if an extinction risk assessment using ecological or demographic methods predicts a high probability of persistence for a particular population, but levels of observed within-population genetic variability are low, then historical (or infrequent) events not captured in the assessment may need to be considered. Low levels of within-population genetic variation may indicate the occurrence of environmental catastrophes or other events that have caused population bottleneck or founder events not detectable in short-term demographic or ecological surveys (e.g., Fig. 2). Unless populations are tracked for many generations, patterns of genetic variation may be the only way to reconstruct or infer the occurrence of catastrophic events that may be crucial in terms of extinction risk (Mangel and Tier 1994, Young 1994, Foley 1996).
A second discrepancy may arise when ecological or demographic methods predict a low probability of persistence for a population, but within-population levels of variability are relatively high. A potential example is provided by bull trout (Salvelinus confluentus) populations in streams of the Lake Pend Oreille basin, Idaho, United States. Extinction risk assessments based on time series of redd (gravel pits excavated by female trout for egg deposition) counts suggested that bull trout populations in streams with consistently low redd counts were likely to go extinct within the next 100 years (Rieman and McIntyre 1993). Recent genetic analyses (Spruell et al. 1999) revealed, however, that levels of genetic variability within populations were not related to population size as indexed by redd counts. This finding has motivated the development of more realistic demographic models (D. Lee and B. Rieman, U.S.D.A. Forest Service Rocky Mountain Research Station, personal communication), increased scrutiny of redd counts as an index of population size, and re-evaluation of the population structure of bull trout in general (Dunham and Rieman 1999).
A similar example can be found for pika (Ochotona princeps). Extinction and recolonization dynamics of habitat patches in a pika metapopulation suggested loss and coalescence of genetic variation (Gilpin 1991, Smith and Gilpin 1997). However, analysis of multilocus DNA fingerprinting data revealed high levels of heterozygosity (Peacock and Smith 1997). Mark-recapture data, combined with genetic data, revealed an important component of gene flow, among-patch movement in between extinction events, not captured by extinction-recolonization dynamics. The additional component of juvenile dispersal to occupied patches appears to be important to patch occupancy rates, patch persistence, and maintenance of genetic variation (Peacock and Smith 1997).
As with patterns of within-population variability, patterns of genetic variation among populations may provide useful information about extinction risk. Patterns of genetic variation among populations are often used to infer levels of migration or gene flow. Migration rates from genetic data are typically derived from F statistics or analogous measures of among-population genetic variability (Neigel 1997). This approach assumes a migration-drift equilibrium, which may not be valid in many situations, especially for organisms prone to local population bottlenecks or founder events (Boileau et al. 1992, Slatkin 1993). Species with such dynamics may pose difficulties in terms of estimating demographic parameters (e.g., dispersal), but patterns of genetic differentiation among populations may be useful for identifying populations at risk of extinction.
When populations become subdivided by habitat fragmentation, founder events, or similar biogeographic or ecological processes, among-population genetic differentiation will theoretically approach a migration-drift equilibrium at a rate determined by time since divergence, migration rate, and population size (Boileau et al. 1992). The approach of populations to a migration-drift equilibrium can take many generations for some species, particularly when founder events or genetic bottlenecks are followed by rapid population increases to a relatively large size (Boileau et al. 1992).
Slatkin (1993) proposed statistical methods for detecting nonequilibrium genetic differentiation in natural populations. When genetic differentiation is a function of geographic distance between local populations, pairwise estimates of gene flow should be inversely related to interpopulation distances at equilibrium (Slatkin 1993). Low estimates of gene flow, coupled with lack of isolation by distance, may indicate nonequilibrium genetic differentiation due to bottleneck and founder effects, or extreme isolation (Boileau et al. 1992, Slatkin 1993, Britten et al. 1995). The result is that genetic differentiation may be overestimated and gene flow underestimated.
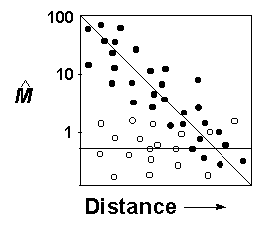
If populations experiencing isolation due to habitat fragmentation or frequent bottleneck and founder events are at greater risk of extinction, then the isolation by distance method (Slatkin 1993) may be used to identify at-risk populations (Fig. 3). Pairwise estimates of migration should be an inverse function of the geographic distance separating populations at equilibrium (Slatkin 1993; see Fig. 2). Although not yet described for any data sets that are familiar to us, it may be that unique functions (e.g., curvilinear or piecewise) may be necessary to describe isolation by distance when dispersal is not a linear function of geographic distance. For simplicity in this discussion, we assume a linear relationship (Fig. 3).
A species may consist of both equilibrium and nonequilibrium local populations (Hellberg 1995, Green et al. 1996; see Fig. 3). For example, patterns of nonequilibrium divergence suggesting low migration rates due to isolation or severe constrictions in population size (e.g., open circles in Fig. 3) may indicate isolation by fragmentation, or perhaps the genetic legacy of a catastrophic disturbance. Similar patterns of nonequilibrium divergence have been linked to long-term climate change and fragmentation of aquatic habitats for southern spotted frog populations (Rana pretiosa, Green et al. 1996). In the case of a group of pocket gopher (Thomonys bottae) populations in central California, low estimates of gene flow and nonequilibrium divergence may have resulted from extreme isolation (Slatkin 1993; see also Britten et al. 1995). For a second group of pocket gopher populations, lack of isolation by distance and high estimates of gene flow suggested an alternative pattern of transient disequilibrium produced by recent colonization events (Slatkin 1993).
The extent to which patterns of genetic variability reflect extinction risk will depend upon how alternative demographic and ecological conditions are related to extinction risk. For example, we suggest that patterns of within-population genetic variability may indicate the occurrence of past catastrophes, events that may cause local extinctions. Although some theoretical work suggests that conventional assumptions about extinction risk from catastrophes may be exaggerated (Lande 1993), empirical evidence from natural populations (e.g., Young 1994, Foley 1996) suggests that catastrophes may be of sufficient magnitude and frequency to pose substantial risks to the persistence of local populations (see also Mangel and Tier 1994).
It is also likely that some species with limited within-population variability, or nonequilibrium population structure, may be well adapted to persist in the face of extreme isolation or small population size. This may be the case for species that inhabit naturally isolated, but relatively stable habitats.
Finally, past threats to populations (e.g., harvesting, land use, disease, etc.) may no longer be relevant to present or future extinction risk. This possibility must be considered carefully because information on past extinctions may not be useful in contemporary risk assessments and vice versa.
Different methods and approaches to estimating the risk of extinction integrate information on a variety of spatial and temporal scales (Table 1). For example, incidence functions (Hanski 1997) incorporate information on broad-scale patterns of local extinctions that may have occurred in the recent past, or during historical events that occurred decades, hundreds, or even thousands of years (or generations) ago. Furthermore, incidence functions often provide only a "snapshot" or static picture of species' occurrence. For many species, it may be difficult to study temporal patterns of occurrence, because extinction and recolonization of habitats may occur on very long time scales (e.g., Dunham and Rieman 1999).
Methods of assessment based on detailed demographic data from extant populations, such as population viability analysis, are generally limited to one or a few local populations and relatively short time scales, which may not represent the regional dynamics of a species (Middleton and Nisbet 1997). Furthermore, large data requirements and model uncertainty may limit the utility of demographic viability models to produce reliable extinction risk estimates (Mills et al. 1996, Beissinger and Westphal 1998).
Patterns of genetic variability are based on extant populations, and should incorporate information from a large number of populations. This is because processes occurring on a variety of spatial and temporal scales may influence patterns of genetic variability. There are no simple or general guidelines for exactly how genetic, demographic, and ecological information should be integrated. However, the examples presented here illustrate that the complexity of long-term population dynamics may not be revealed using any single approach. Here, we emphasize the potential of genetic information to complement inferences from demographic and ecological approaches and encourage managers to carefully consider the evidence from each of these diverse sources of information in extinction risk assessments.
Responses to this article are invited. If accepted for publication, your response will be hyperlinked to the article. To submit a comment, follow this link. To read comments already accepted, follow this link.
We thank C. Ray and two anonymous reviewers for constructive comments on earlier versions of this manuscript. J. B. Dunham and M. M. Peacock were supported, in part, by the U.S.D.A. Forest Service Rocky Mountain (formerly Intermountain) Research Station (INT-96089-RJVA), and U.S. Fish and Wildlife Service, Region 1 (DOI-FW-1960007), with additional support from the Biological Resources Research Center, University of Nevada-Reno. J. L. Nielsen acknowledges the support of the U.S.D.A. Forest Service Pacific Southwest Research Station.
Allendorf, F. W., D. Bayles, D. L. Bottom, K. P. Currens, C. A. Frissell, D. Hankin, J. A. Lichatowich,, W. Nehlsen, P. C. Trotter, and T. H. Williams. 1997. Prioritizing Pacific salmon stocks for conservation. Conservation Biology 11:140-152.
Avise, J. C., J. Arnold, R. M. Ball, E. Bermingham, T. Lamb, J. E. Neigel, C. A. Reeb, and N. C. Saunders. 1987. Intraspecific phylogeography: the mitochondrial bridge between population genetics and systematics. Annual Review of Ecology and Systematics 18:489-522.
Beissinger, S. R., and M. I. Westphal. 1998. On the use of demographic models of population viability in endangered species management. Journal of Wildlife Management 62:821-841.
Boileau, M. G., P. D. N. Hebert, and S. S. Schwartz. 1992. Non-equilibrium gene frequency divergence: persistent founder effects in natural populations. Journal of Evolutionary Biology 5:25-39.
Boyce, M. S. 1992. Population viability analysis. Annual Review of Ecology and Systematics 23:481-506.
Britten, H. B., P. F. Brussard, D. D. Murphy, and P. R. Ehrlich. 1995. A test for isolation-by- distance in central Rocky Mountains and Great Basin populations of Edith's checkerspot butterfly (Euphydryas editha). Journal of Heredity 86:204-210.
Burgman, M. A., A. S. Ferson, and R. Akçakaya. 1993. Risk assessment in conservation biology. Chapman and Hall, New York, New York, USA.
Caro, T. M., and M. K. Laurenson. 1994. Ecological and genetic factors in conservation: a cautionary tale. Science 263:485-486.
Caughley, G. 1994. Directions in conservation biology. Journal of Animal Ecology 63:215-244.
DeMarais, B. D., T. E. Dowling, and W. L. Minckley. 1993. Post-perturbation genetic changes in populations of endangered Virgin River chubs. Conservation Biology 7:334-341.
Dunham, J. B., and B. E. Rieman. 1999. Metapopulation structure of bull trout: influences of habitat size, isolation, and human disturbance. Ecological Applications 9, in press.
Foley, P. 1996. Extinction models for local populations. Pages 215-246 in I. A. Hanski and M. E. Gilpin, editors. Metapopulation biology: ecology, genetics, evolution. Academic Press, New York, New York, USA.
Frankham, R. 1995. Inbreeding and conservation: a threshold effect. Conservation Biology 9:792-799.
_______ . 1996. Relationship of genetic variation to population size in wildlife. Conservation Biology 10:1500-1508.
Gilpin, M. E. 1991. The genetic effective size of a metapopulation. Pages 165-175 in M. E. Gilpin and I. Hanski, editors. Metapopulation dynamics: empirical and theoretical investigations. Academic Press, London, UK.
Gilpin, M. E., and M. E. Soulé. 1986. Minimum viable populations: processes of species extinction. Pages 19-34 in M. E. Soulé, editor. Conservation biology: the science of scarcity and diversity. Sinauer Associates, Sunderland, Massachusetts, USA.
Given, D. R., and D. A. Norton. 1993. A multivariate approach to assessing threat and for priority setting in threatened species conservation. Biological Conservation 64:57-66.
Goodman, D. 1987. The demography of chance extinction. Pages 11-34 in M. E. Soulé, editor. Viable populations for conservation. Cambridge University Press, Cambridge, Massachusetts, USA.
Green, D. M., T. F. Sharbel, J. Kearsley, and H. Kaiser. 1996. Postglacial range fluctuation, genetic subdivision and speciation in the western North American spotted frog complex Rana pretiosa. Evolution 50:374-390.
Hanski, I. 1997. Predictive and practical metapopulation models: the incidence function approach. Pages 21-25 in D. Tilman and P. Kareiva, editors. Spatial ecology: the role of space in population dynamics and interspecific interactions. Monographs in Population Biology 30. Princeton University Press, Princeton, New Jersey, USA.
Hastings, A., and S. Harrison. 1994. Metapopulation dynamics and genetics. Annual Review of Ecology and Systematics 25:167-188.
Hedrick, P. W. 1996. Bottleneck(s) or metapopulation in cheetahs. Conservation Biology 10:897-899.
Hedrick, P. W., and M. E. Gilpin. 1996. Genetic effective size of a metapopulation. Pages 165-191 in I. Hanski and M. E. Gilpin, editors. Metapopulation biology: ecology, genetics and evolution. Academic Press, New York, New York, USA.
Hedrick, P. W., R. C. Lacy, F. W. Allendorf, and M.E. Soulé. 1996. Directions in conservation biology: comments on Caughley. Conservation Biology 10:1312-1320.
Hellberg, M. E. 1995. Stepping-stone gene flow in the solitary coral Balanophylla elegans: equilibrium and nonequilibrium at different spatial scales. Marine Biology 123:573-581.
Lande, R. 1993. Risks of population extinction from demographic and environmental stochasticity and random catastrophes. American Naturalist 142:911-927.
_______ . 1995. Mutation and conservation. Conservation Biology 9:782-791.
Leberg, P. L. 1992. Effects of population bottlenecks on genetic diversity as measured by allozyme electrophoresis. Evolution 46:477-494.
Mace, G. M., and R. Lande. 1991. Assessing extinction threats: toward a reevaluation of IUCN threatened species categories. Conservation Biology 5:148-157.
Mangel, M., and C. Tier. 1994. Four facts every conservation biologist should know about persistence. Ecology 75:607-614.
Middleton, D. A. J., and R. M. Nisbet. 1997. Population persistence time: estimates, models, and mechanisms. Ecological Applications 7:107-117.
Milligan, B. G., J. Leebens-Mack, and A. E. Strand. 1994. Conservation genetics: beyond the maintenance of marker diversity. Molecular Ecology 3:423-435.
Mills L. S., S. G. Hayes, C. Baldwin, M. J. Wisdom, J. Citta, D. J. Mattson, and K. Murphy. 1996. Factors leading to different viability predictions for a grizzly bear data set. Conservation Biology 10:863-873.
Moritz, C. 1994. Applications of mitochondrial DNA analysis in conservation: a critical review. Molecular Ecology 3:401-411.
Nei, M., T. Maruyama, and R. Chakraborty. 1975. The bottleneck effect and genetic variability in populations. Evolution 29:1-10.
Neigel, J. E. 1997. A comparison of alternative strategies for estimating gene flow from genetic markers. Annual Review of Ecology and Systematics 28:105-128.
Peacock, M. M., and A. T. Smith. 1997. The effect of habitat fragmentation on dispersal patterns, mating behavior, and genetic variation in a pika (Ochotona princeps) metapopulation. Oecologia 112:524-533.
Pimm, A. L., H. L. Jones, and J. Diamond. 1988. On the risk of extinction. American Naturalist 132:757-785.
Richards, C., and P. L. Leberg. 1996. Temporal changes in allele frequencies and a population's history of severe bottlenecks. Conservation Biology 10:832-839.
Saccheri, I., M. Kuussaari, M. Kankare, P. Vikman, W. Fortelius, and I. Hanski. 1998. Inbreeding and extinction in a butterfly metapopulation. Nature 392:491-493.
Schoener, T. W., and D. A. Spiller. 1992. Is extinction rate related to temporal variability in population size? An empirical answer for orb spiders. American Naturalist 139:1176-1207.
Shaffer, M. L. 1981. Minimum population sizes for species conservation. BioScience 31:131-134.
Simberloff, D. 1988. The contribution of population and community biology to conservation science. Annual Review of Ecology and Systematics 19:473-512.
Slatkin, M. 1985. Gene flow in natural populations. Annual Review of Ecology and Systematics16:393-430.
_______ . 1993. Isolation by distance in equilibrium and non-equilibrium populations. Evolution 47:264-279.
Smith, A. T., and M. E. Gilpin. 1997. Spatially correlated dynamics in a pika metapopulation. Pages 407-423 in I. Hanski and M. E. Gilpin, editors. Metapopulation biology: ecology, genetics, and evolution. Academic Press, London, UK.
Spruell, P., B. E. Rieman, K. L. Knudsen, F. M. Utter, and F. W. Allendorf. 1999. Genetic population structure within streams: microsatellite analysis of bull trout populations. Ecology of Freshwater Fish, in press.
Taylor, B. L. 1995. The reliability of using population viability analysis for risk classification of species. Conservation Biology 9:551-558.
Tracy, C. R., and T. L. George. 1992. On the determinants of extinction. American Naturalist 139:102-122.
Young, T. P. 1994. Natural die-offs of large mammals: implications for conservation. Conservation Biology 8:410-418.
Address of Correspondent:
Jason Dunham
Biological Resources Research Center
University of Nevada
Reno, Nevada, USA 89557
Phone: 541-752-3683
Fax: 702-784-1369
jdunham@proaxis.com
*The copyright to this article passed from the Ecological Society of America to the Resilience Alliance on 1 January 2000.

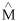 ) and
geographic distance (log scale). Solid circles represent populations
with equilibrium divergence and open circles represent nonequilibrium
genetic divergence.
) and
geographic distance (log scale). Solid circles represent populations
with equilibrium divergence and open circles represent nonequilibrium
genetic divergence.