ERRATUM. In the original published version of Appendix 3, a number of the equations were missing characters (principly minus signs). The corrected appendix is provided in full below.

Appendix 3 (corrected). Generosity in a continuous partial equilibrium static model of externalities.

Partial equilibrium models of externalities assume a given set of prices to firms that are interacting with production connectedness (Runge 1981, Varian 1994). Runge formulates a continuous model that reduces to a prisoner's dilemma or an assurance game, depending on the assumptions about cost functions. This appendix reviews his demonstration of the suboptimality of private decisions, and demonstrates the optimality of a solution in which the firms are required to divide their profits among each other.

Runge defines the following problem, Let:

Thus,

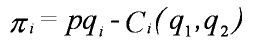
An externality arises if:

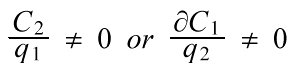
A social optimum maximizes joint profit, where

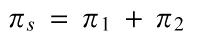
Therefore

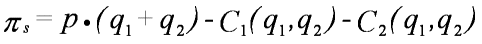
The first order conditions are

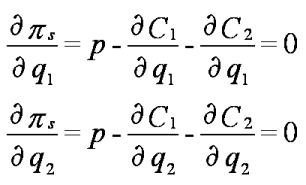
The solution to these two equations in two unknowns gives the optimum level of production for each of the two goods.

Now examine a market equilibrium where each firm keeps its profits. The individual firm, for instance firm 1, solves the problem of maximizing its profits,

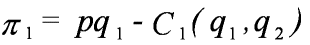
and the first order condition is

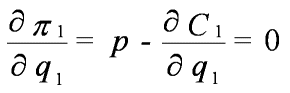
which will give a different value of q₁ than the social optimum, because the first order condition omits the term involving the partial derivative of the second firm's cost function.

Now suppose

u = Share of firm 1's profit kept by firm 1

v = Share of firm 2's profit kept by firm 2

Both u and v can hold a value from zero to one.

If firm 1's net return is defined by

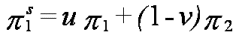
Then firm 1's maximization problem is to maximize

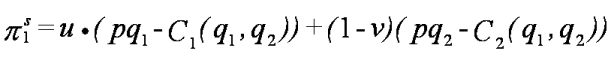
The first order condition is

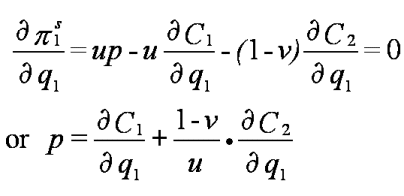
Thus, if u = v = 1/2, the symmetric generosity rule, then firm 1's first order condition equals the social first order condition.

This example can be generalized to many firms. Let T_j = return to firm j after application of forced generosity using the notation of section II above,

Let

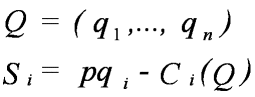
Then, the return to firm j is determined as follows:

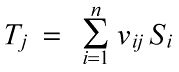
where

v_ij = share of S_i that is distributed to firm j.

Examining the maximization problem for firm 1

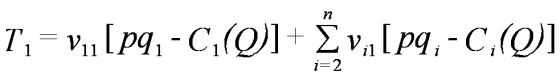
The first order condition for the optimum choice of q₁ is

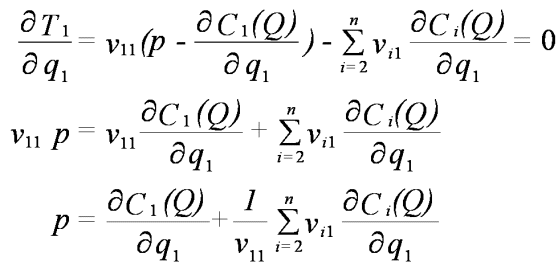
If a symmetric generosity rule applies, then v_ij = 1/n and

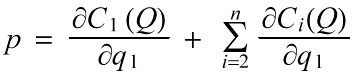
This condition is identical to the condition for social optimality.

Runge points out that if the cost functions are separable, each firm can solve its individual maximization problem without knowing what the other firms have decided. This is true for both the pure private profit case or the symmetric generosity case. Separability means that each cost function is additive:

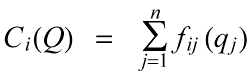
as a result,

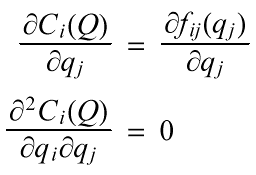
If the cost functions are not separable, then an individual firm cannot determine its point of maximum profit without knowing what other firms are doing in either the pure private profit case or the symmetric generosity case. Non-separability creates a situation in which the need for coordinated action is clear to each firm in either case. Because of the complexity of selecting any equilibrium set of production amounts Q, Runge (1981) does not present a solution. Instead, he points out that the separable case creates a prisoner's dilemma situation, and asserts that in the non-separable case an assurance game results.

To make some headway for Runge's non-separable case, examine incentives to defect from a jointly optimal solution, Q^*, however that solution was adopted. Suppose that through some mechanism (such as a series of public discussions at village feasts), all firms are operating at a socially optimal values q₁^*,......q_n^*. What are the incentives to defect from this social optimum under, first, a pure selfishness rule and, second, a symmetric generosity rule?

A defection by firm 1 would be an increase dq₁ from q₁^* at the social optimum, since all first partial derivatives are positive,

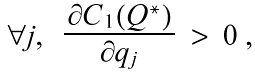
it follows that in the selfish case, when v_ii = 1 and v_ij = 0,

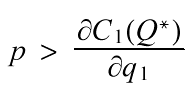
and an increase in q₁^* to q₁^* + dq would increase the profit of the first firm. There is a clear incentive to defect.

In the case of symmetric generosity, however, an increase in firm 1's profit is matched by a decrease in the profit of all of the other firms. When v₁₁ = v_ij = 1/n, then there is no incentive to defect, because the condition for a social optimum is that for the first firm, price is equal to the sum of the marginal costs of all of the firms with respect to the output of the first firm:

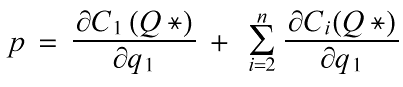
This same condition applies to all firms. The selected outputs, Q*, are stable.