|
|
|
Copyright ©1998 by The Resilience Alliance*
Judith L. Anderson. 1998. Embracing uncertainty: The interface of Bayesian statistics and cognitive psychology. Conservation Ecology [online] 2(1): 2. Available from the Internet. URL: http://www.consecol.org/vol2/iss1/art2/
A version of this article in which text, figures, tables, and appendices are separate files may be found by following this link.
Synthesis Embracing Uncertainty: The Interface of Bayesian Statistics and Cognitive Psychology Judith L. Anderson
School of Resource and Environmental Management, Simon Fraser University
- Abstract
- Introduction
- The Bayesian Approach to Uncertainty
- Bayesian and Classical Analysis: an Example
- Cultural Evolution and Bayesian Analysis
- Would Bayesian Analysis Benefit from Standardization?
- Adapting Bayesian Analysis to the Human Mind: Guidelines from Cognitive Science
- Responses
- Acknowledgments
- Literature Cited
Ecologists working in conservation and resource management are discovering the importance of using Bayesian analytic methods to deal explicitly with uncertainty in data analyses and decision making. However, Bayesian procedures require, as inputs and outputs, an idea that is problematic for the human brain: the probability of a hypothesis ("single-event probability"). I describe several cognitive concepts closely related to single-event probabilities, and discuss how their interchangeability in the human mind results in "cognitive illusions," apparent deficits in reasoning about uncertainty. Each cognitive illusion implies specific possible pitfalls for the use of single-event probabilities in ecology and resource management. I then discuss recent research in cognitive psychology showing that simple tactics of communication, suggested by an evolutionary perspective on human cognition, help people to process uncertain information more effectively as they read and talk about probabilities. In addition, I suggest that carefully considered standards for methodology and conventions for presentation may also make Bayesian analyses easier to understand.
KEY WORDS: cognitive psychology; judgment under uncertainty; cognitive illusion; Bayesian statistical analysis; Bayesian decision analysis; probability; frequency; expert elicitation of probabilities.
Conservation ecologists, resource managers, and policy makers are developing an appreciation for the value of explicitly including uncertainty when they analyze ecological processes. Although it is unfamiliar to many applied ecologists, Bayesian statistical analysis is well suited to this purpose. It directly analyzes the probability of a hypothesis, allowing scientists and managers to formally update their beliefs in a variety of experimental and nonexperimental situations (Ellison 1996). To raise awareness of Bayesian analysis, several ecologists have presented strong arguments promoting its use in contexts of conservation and resource management (Crome et al. 1996, Ellison 1996, Ludwig 1996, Taylor et al. 1996, Wolfson et al. 1996). However, despite its advantages, Bayesian analysis is not likely to become widely accepted by nonstatisticians unless its proponents make it more easily understood.
In this paper, I briefly introduce Bayesian analysis and describe how it can complement "classical" statistics in situations where uncertainty must be taken into account. I then show how the acceptance of classical and Bayesian statistics among applied ecologists could be viewed as examples of cultural evolution. This interpretation leads to the discussion of two possible barriers to the understanding and use of Bayesian analysis. First, tactics for reporting Bayesian results and estimating prior probabilities are highly variable. Second, decimal probabilities are hard for most people to understand and process intuitively. I present ideas and experimental results from cognitive psychology that may help to explain and ameliorate this difficulty.
Statistical analysis is often presented in introductory courses and textbooks as a unique, anonymous, and authoritative method for dealing with uncertainty. This myopic view disguises the rich history and variety of statistical practice. The monolith known as "classical" or "frequentist" statistics, for example, is actually an uncomfortable hybrid between two distinct methods of hypothesis testing, developed in the first half of this century: that of R. A. Fisher, emphasizing rejection of a null hypothesis, and that of J. Neymann and E. S. Pearson, emphasizing decisions between two mutually exclusive hypotheses (Sedlmeier and Gigerenzer 1989, Gigerenzer 1991). Typical courses in statistics present even less information about a third tradition of analysis based on the work of the Reverend Thomas Bayes, originally published in 1763 (Lee 1989). Bayes' approach focuses on estimating the probability that a hypothesis is true and updating that probability as data accumulate.
The goal of all statistical analysis, ultimately, is to help people use data to rationally update their beliefs about scientific hypotheses. The various traditions in statistics approach this goal in different ways. The Fisherian and Neymann-Pearson traditions both assume that data are collected in a highly structured experimental design, including a well-defined statistical null hypothesis that follows from the more general scientific hypothesis (or model) under examination. The familiar P value answers the question, "If the statistical null hypothesis were true, what is the probability that we would observe these data, or more extreme data, in an experiment of this type?" Thus, the P value is a statement about the data, not about the scientific hypothesis. Nonetheless, by convention, if the probability of observing the data is sufficiently small, a decision about the statistical null hypothesis follows: it is rejected.
"Rejection" sounds like an all-or-nothing conclusion about the statistical hypothesis. In practice, however, ecologists usually interpret the inference from a single experiment cautiously, as one piece of evidence bearing on the scientific hypothesis. Traditionally, scientists have depended on a separate process to update beliefs in the scientific hypothesis: the more or less structured combination of repeated, independent experiments and research synthesis (Shadish 1989, Underwood 1990, Cooper and Hedges 1994).
Bayesian analysis, in contrast, is explicitly a process for updating beliefs in hypotheses. It defines the probability of a hypothesis as an observer's confidence or degree of belief in it, and addresses the question, "Given her previous beliefs, how should she revise the probability assigned to the hypothesis in light of the data at hand?"
The actual calculations required to answer this question are elementary in principle, although usually complex in practice. The inputs to a Bayesian analysis are: (1) estimates of "prior" probabilities, the degree of confidence in each hypothesis before the data are seen; and (2) probabilities of the data, the probability that the data would be observed if each hypothesis were true. These inputs are combined using Bayes' theorem to produce "posterior" probability estimates that represent the updated degree of belief in each hypothesis under consideration (Lee 1989, Morgan and Henrion 1990, Ellison 1996). The general idea is that, if the experimenter had a high degree of belief in a specific hypothesis based on past experience, and she now observes data that would be likely to occur given that hypothesis, her posterior (after the data) confidence in the hypothesis should be strengthened.
Bayesian analysis differs from classical analysis of a single experiment in several profound ways. In fact, Bayesian and classical statisticians sometimes divide themselves into opposing camps. Each rejects the other approach because of its limitations and weaknesses (Lee 1989, Berry and Stangl 1996, Dennis 1996, Edwards 1996, Ellison 1996, Mayo 1996). The arguments are beyond the scope of this paper, but it is important to mention some differences. First, Bayesian analysis requires prior probability estimates. These quantitative statements of belief or previous experience have no formal place in classical analysis. Second, a Bayesian analysis can assign intermediate degrees of belief or probability to hypotheses, unlike the all-or-nothing inferences "reject/retain the hypothesis." Third, Bayesian analysis can be applied either to discrete hypotheses or to a continuum of hypotheses (Box and Tiao 1973). Finally, Bayesian data need not come from a completed experimental design, although the observations must be structured so that the analyst can estimate the probability of observing the data under each hypothesis considered.
As long as its limitations are understood and respected, Bayesian analysis should prove useful in some circumstances typical of conservation biology and applied ecology. For example, it can estimate, at any point, how much confidence should be placed in each hypothesis under consideration. This flexibility is an advantage where well-designed experiments are impossible, or decisions must be based on incomplete data, e.g., from a long-term monitoring program. In addition, the probabilities assigned to hypotheses by Bayesian statistical analysis can feed directly into a Bayesian decision analysis: a process for rationally analyzing, evaluating, and comparing a range of practical management options in the face of uncertainty (Raiffa 1968, Parkhurst 1984, Maguire 1986, 1988, Morgan and Henrion 1990, Maguire and Boiney 1994).
Let us compare Bayesian and classical analyses of a simple problem in conservation ecology. Suppose that an ecologist needs an indicator for the presence of breeding Marbled Murrelets in old-growth forest on the west coast of Vancouver Island. An indicator for ecological monitoring should be a simple observation that indicates with high probability something about the ecosystem that is important, but not easy to observe. A possible candidate, in this case, is the existence of suitable nest sites: big, horizontal branches with a good layer of moss and lichen. The investigator has designed a quick, standardized survey to detect those branches and has tried it out on 1000 stands, producing the data shown in Table 1.
Table 1. Basic data for the Marbled Murrelet example.
|
Bayesian analysis
From a Bayesian point of view, the question is: In the future, if the ecologist observes potential nest sites during a standardized survey in a particular stand X, what is the probability that Marbled Murrelets actually breed in the stand?
The hypotheses under consideration are
H1: Murrelets are nesting in stand X ;
H2: Murrelets are not nesting in stand X .
The "data" will be "suitable nest sites observed/not observed."
From Table 1, the following components of the Bayesian analysis can be estimated.
p(H1) = prior probability of H1 = 50/1000 = 0.05 (i.e., the probability if there were no survey data on stand X);
p(H2) = prior probability of H2 = 950/1000 = 0.95;
p(D|H1) = probability of observing the data (suitable nest sites) when H1 is true (murrelets are nesting in stand X) = 46/50 = 0.92;
p(D|H2) = probability of observing the data (suitable nest sites) when H2 is true (murrelets are not nesting in stand X) = 142/950 = 0.15;
p(H1|D) = probability that H1 is true, given the data; i.e., the probability that murrelets are nesting in stand X, given the observation of suitable nest sites on the standard survey. This is what the ecologist wants to know. To calculate it, he must apply Bayes' theorem.
Bayes' theorem (for two hypotheses):
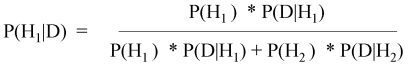
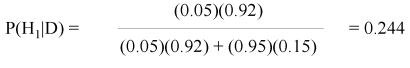
The Bayesian analysis suggests that the standardized survey is not a particularly good indicator of the presence of nesting marbled murrelets. If potential nest sites are observed in a stand during a standard survey, the probability is only 0.24 that murrelets are actually nesting there.
Classical analysis
Classical analysis of this problem addresses a slightly different set of hypotheses:
H0: Observation of suitable nest sites is not associated with the presence of nesting murrelets.
HA: Observation of suitable nest sites is associated with the presence of nesting murrelets.
A chi-square analysis of the data in Table 1 confirms what seems evident by inspection. With a highly significant probability (P < 0.001), the ecologist rejects the null hypothesis. Now the question becomes, how strong is this association? Zar (1996) lists several suitable measures of correlation for categorical data. For the data in Table 1, their values range from 0.430 (Cramer phi2), to 0.708 (Ives and Gibbon rn), to 0.970 (Yule Q).
The categorical correlation coefficients do not agree well among themselves. They also do not address quite the same question as the Bayesian analysis, because they provide little direct information about the truth value of H1. Moreover, if the correlation coefficients were to be (mis)interpreted as indicators of the credibility of H1, they would generally present a more optimistic picture of the utility of the standard survey than does the Bayesian analysis.
Given its potential utility in applied and conservation ecology, it seems surprising that Bayesian analysis is relatively uncommon. However, logical and theoretical virtue is not sufficient to encourage its use by managers and scientists. The spread of a new idea or practice is an example of cultural evolution (in this case, within the scientific community). It is best understood as a social and psychological phenomenon.
Scientific ideas and practices as "memes"
Successful communication is the key to transforming a good idea into widespread practice. "Much of what we do in conservation biology is essentially worthless if it is not translated into effective policy" (Meffe and Viederman 1995: 327). Technical sophistication is not a substitute for good communication, but, in fact, can exacerbate problems resulting from the failure of decision makers to understand important information (Walters 1986, Clark 1993). Furthermore, effective use of information requires congruence between the scientific models presented and the decision maker's conception of the problem (Brunner and Clark 1997, Weeks and Packard 1997).
Even when the facts or ideas involved are abstract, human communication is a biological process, because the mind is a product of natural selection. For example, Brunner et al. (1987) list four processes indicating that results of a data analysis have been communicated to decision makers or other scientists: assimilation (reconciliation of the information presented with the user's own knowledge); utilization (of the language, form, and content of the analysis in subsequent applications); recall; and recognition. These processes are, in a sense, organic. They depend not only on the author's presentation of the material, but also on its fit to the reader's mind, just as an enzyme must match the shape of a molecule it is to modify.
Carrying the biological metaphor further, various approaches to data analysis might be interpreted as "memes." A meme is the cultural analog of a gene, a unit of thought or behavior pattern that depends on the human mind for its existence and "replicates" itself accurately when transmitted to others (Dawkins 1976, Parson and Clark 1995). This analogy suggests that memes "survive" by being remembered and "reproduce" when transmitted from one person to another through social interactions such as teaching, role modeling, persuasion, and so on. These processes of cultural evolution, by which memes change frequency in a culture, can be analyzed quantitatively using models derived from population genetics (Cavalli-Sforza and Feldman 1981, Boyd and Richerson 1985).
The biological metaphor further suggests that a meme is "well adapted" to its primary host, the human brain, if it is easily assimilated and shared by average members of the community using ordinary language. For example, many of the tactics used to make computer applications "user-friendly" may be well-adapted memes. For a "data analysis meme," the four processes of Brunner et al. (1987) (assimilation, utilization, recall, and recognition) could be interpreted as the gauge of its adaptation. They emphasize the importance of ordinary human interaction to the "symbiosis" between the meme and its primary host, the human mind. A data analysis meme may "survive" and "reproduce" in other cultural media such as scientific journals, but these are secondary hosts. The more reliant a meme is on secondary hosts, the less likely it is to become widespread or used readily, because it requires unusual levels of training or specialized media to be transmitted accurately.
Classical statistical practice: a successful meme?
Classical statistical practice has been spectacularly successful. As M. G. Kendall described it in 1942, "They [statisticians] have already overrun every branch of science with a rapidity of conquest rivaled only by Attila, Mohammed, and the Colorado beetle" (Gigerenzer 1991: 258). Although classical statistical practice has abetted progress in pure and applied science, it has done so despite its weaknesses. These include internal inconsistencies that result from the hybridization of Fisherian and Neymann-Pearson methods, the loss of information through the neglect of statistical power, failure directly to answer questions about the truth value of hypotheses, and the fact that many practitioners do not thoroughly understand it (Sedlmeier and Gigerenzer 1989, Gigerenzer 1991, Ellison 1996). Thus, the dominant position of classical statistics does not seem justified by its logical or theoretical virtues. Instead, the entrenchment of classical statistics may be attributable, in part, to factors that enhance its effectiveness as a collection of memes.
First, cultural evolution theory suggests that memes "survive" and "reproduce" better when they are well-adapted to structures of the human mind. This idea is supported by empirical evidence from the social sciences. For example, the mathematical concepts and methods that people learn most easily are those that map onto innate cognitive structures for counting (Dehaene 1997). In the case of classical statistics, empirical evidence supports a correspondence between ideas of hypothesis-testing and processes that people use to make intuitive inferences. One example is "signal detection theory" (Tanner and Swets 1954), a model for the process by which the human mind distinguishes an object ("signal") from "noise." The signal detection model is directly parallel to Neymann-Pearson hypothesis-testing (Gigerenzer and Murray 1987). It assumes that the mind decides what it perceives by comparing incoming stimuli with two distributions, one expected from "noise" (the null hypothesis), and another expected from a "signal" (the alternative hypothesis). Features of this cognitive model have proven especially fruitful in empirical studies, which document the existence of two types of error ("false alarms" and "misses"), corresponding to Type I and Type II errors. In addition, subjects exhibit the ability to adjust the decision process according to difference between the two distributions, corresponding to Neymann-Pearson effect size. Although no simple model can capture the complexity of human cognition, signal detection theory suggests that hypothesis-testing may correspond to innate human cognitive processes. Thus, the ideas of hypothesis-testing are relatively easy for people to understand and use.
Second, conventions for reporting results of classical statistical analysis enable authors and readers to share common expectations (e.g., P values, sample sizes). The conventions summarize large amounts of data into statements, in ordinary language, about a limited set of hypotheses (H0, the null hypothesis, and HA, the alternative hypothesis). This summary is made possible because the results feed directly into a standardized decision structure. The decision rule is, "If P < 0.05 (critical alpha), the evidence supports HA; if P greater than or equal to 0.05, the evidence supports H0." In the meme analogy, ideas that can be expressed verbally and fit a consistent pattern are likely to survive (be remembered) and replicate (be communicated accurately to others).
The conventional decision structure of hypothesis-testing is notably robust. It makes intuitive sense and enables people to assimilate results of the analysis even when they are hazy about all of its logical implications. For example, the neglect of statistical power has certainly resulted in loss of information and has probably diminished the quality of management decisions based on classical statistical inference (Peterman 1990, Fairweather 1991). Nonetheless, ecologists have embraced the methods of classical statistics and the field has progressed under its paradigm (Dennis 1996).
Finally, the conventions of classical statistics were initially convincing enough that they were endorsed and enforced by dominant members of the scientific community: professors and journal editors (Sedlmeier and Gigerenzer 1989). Modeling and persuasion by socially dominant individuals are important mechanisms for cultural evolution (Boyd and Richerson 1985).
I have suggested that classical statistics, as a collection of memes, enjoys at least three independent advantages: It seems well-adapted to the human mind, the conventions for reporting provide consistent summaries of results in ordinary language, and dominant members of the scientific community have encouraged its use. In the following sections, I argue that these very characteristics may currently represent weaknesses for Bayesian statistics, which lacks conventions and seems to be poorly adapted to the human mind. In each case, I discuss how these deficiencies might be turned to advantage. Finally, I conclude by pointing out how leaders in the ecological community might use their influence to improve the utility of Bayesian analyses in conservation and applied ecology.
Reporting posterior probabilities
In contrast to the reporting conventions of classical statistics, Bayesian analyses seem to be completely unstandardized. The results of Bayesian analyses are always posterior probability estimates, but they are presented with a wide variety of terminology and graphic or tabled formats (e.g., Thompson 1992, Hilborn et al. 1994, Stahl et al. 1994, Pascual and Hilborn 1995, Adkison and Peterman 1996, Crome et al. 1996, Edwards 1996). Even in papers intended for an audience of ecologists and conservation biologists, authors tend to assume that readers are familiar with difficult technical concepts such as probability density.
Bayesian reporting practice also seems unreconciled with scientific conventions concerning significant digits. Tables of posterior probability estimates often involve drastic differences among comparable probability estimates. For example, Pascual and Hilborn's (1995) table (reproduced here in Table 2) includes probabilities as low as 0.00006, requiring other estimates in the table to be reported to five significant digits. It is questionable whether any ecological data justify this degree of precision.
Table 2. Example of the probability format. This table reports Bayesian posterior probabilities for the parameters (alpha and beta) of the function relating recruitment to dry-season rainfall, for a population of Serengeti wildebeest (as presented in Pascual and Hilborn 1995: 475).
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Bayesian analysis enjoys a theoretical advantage in its ability to address "fine-grained" hypotheses. A Bayesian analysis can compute probabilities for arbitrarily small ranges of a parameter such as the population mean, mu. Nonetheless, Bayesian analysts often sacrifice this advantage in favor of simpler presentations, similar to those of classical statistics, that enable results to be discussed in ordinary language. For example, Bayesian analysts may divide a continuum into only two or three regions, just as a classical analysts do when they test two coarse hypotheses (such as H0: mu greater than or equal to 0, HA: mu < 0).
Similarly, Bayesian analysts sometimes try to simplify their results by feeding them into a decision analysis that produces inferences or compares management options (e.g., Crome et al. 1996, Taylor et al. 1996, Wolfson et al. 1996). In some ways, this simplifying tactic resembles the decision model for inferences used in classical statistics. However, in contrast to the predictable, simple decision rule for inference in classical statistics, each of these analyses involved a complex, idiosyncratic decision structure. For example, Crome et al. (1996:1112) proposed a decision structure for making inferences about eight different propositions concerning effect size, labeling each "implausible" if the probability assigned to it were <0.1 or "highly likely" if its probability were >0.9. A sample proposition (#7) read: "It is very likely that the effect [size] lies between 0.75 and 1.25; large positive or negative effects are implausible and propositions 3 and 6 are accepted if P1 < 0.1 and P3 < 0.1." Away from the text of Crome et al. (1996), a reader would be unlikely to remember conclusions about the eight propositions, or to transmit them accurately to others, unless he committed to memory all of the details and assumptions of the decision structure.
Estimating prior probabilities
Approaches to the estimation of prior probabilities also vary in ecological Bayesian analyses. For instance, Wolfson et al. (1996, Study 2) and Taylor et al. (1996) used existing data for at least some prior estimates. In contrast, Crome et al. (1996) and Wolfson et al. (1996, Study 1) elicited prior probability estimates from experts. Neither provided any discussion of the validity and reliability of their estimation procedures.
Arbitrary assignment of priors when there is little information about them is also highly variable in both methodology and terminology (e.g., Box and Tiao 1973, Howson and Urbach1989, Press 1989, Hilborn et al. 1994, Walters and Ludwig 1994, Ludwig 1996, Taylor et al. 1996, Sainsbury et al. 1997). Often there is little or no discussion about distinctions among the various approaches to arbitrary priors, or why a particular one was chosen.
Advantages and disadvantages of standardization
Judicious standardization of methods for assigning arbitrary or elicited prior probabilities would probably benefit most analyses. Poorly designed prior probability distributions can result in serious distortions of results (Adkison and Peterman 1996). Moreover, ecological data, unlike data from the physical sciences, are rarely precise enough to overcome those distortions (Ludwig 1996). Therefore, readers routinely should be assured that questions such as the following have been considered: Under what circumstances is an arbitrary prior distribution appropriate? What hypotheses should have non-zero priors? Are the priors independent of the current data? Under what circumstances is expert elicitation appropriate? Has the researcher achieved minimal standards of validity and reliability in expert elicitation? Standardization of methods and conventions for describing them would allow authors to address these important questions briefly.
The advantage of conventions for reporting Bayesian results is less clear-cut. Bayesian analysis is suitable for many questions in conservation and applied ecology precisely because it is so flexible. For example, a simplifying tactic, such as dividing a continuum of posterior probability estimates into two discrete regions, might improve the understanding of readers challenged by the novelty and complexity of Bayesian analyses. However, it would certainly lose essential information in some studies.
This problem deserves consideration by Bayesian analysts, journal editors, and cognitive scientists, who could identify situations in which conventions might be developed and encouraged with relatively little cost. For areas in which standardization seems more problematic, it might be helpful to experiment with several options, monitoring the comprehension of readers and the satisfaction of investigators.
Cognitive research is directly relevant to Bayesian applications in ecology
Cognitive psychologists have long been interested in discovering whether people are good "intuitive statisticians." Their interest implicitly addresses the question, "Is Bayesian analysis a well-adapted meme?" Cognitive research suggests that the answer is "No." When people are asked to reason about probability, the cornerstone of Bayesian analysis, they make predictable, serious mistakes. In this section, I will describe two explanations for this inability. I will then discuss several examples of typical cognitive errors that are relevant to applied ecology, including recent research that suggests how Bayesian analyses might be structured to ameliorate them.
Probabilities can be interpreted in two ways (Gigerenzer 1994, Ellison 1996). The first defines probabilities as the long-run frequency of the occurrence of an event (or of the hypothesis proving true), tallied over many possible instances. The second interpretation, "single-event probability," quantifies the observer's confidence that a particular event will occur, or that a hypothesis is true in a given instance. The probabilities of hypotheses calculated by Bayesian analysis are single-event probabilities.
Unfortunately, the human mind does not process single-event probabilities effectively. A long tradition of experimentation in cognitive psychology shows that even people experienced with statistics routinely make errors when they reason about single-event probabilities. A classic example is the "Linda problem." Subjects read a short description of a woman named Linda, stating that she is interested in political issues, concerned about human rights, and active in her local community. They then assign probabilities to statements about Linda's possible job and avocations, including "Linda works as a bank teller" and "Linda works as a bank teller and is active in the feminist movement." Most people incorrectly assign a higher probability to the latter statement (Gigerenzer and Hoffrage 1995). According to probability theory, it is less likely that a woman would be both a bank teller and a feminist than just a bank teller.
The types of mistakes that people make with probabilities are so predictable and incorrigible that cognitive scientists have traditionally labeled them "cognitive illusions" and have treated them as evidence that humans are not good intuitive statisticians. Tversky and Kahneman (1974), Ayton and Wright (1994), and Gigerenzer and Hoffrage (1995) summarize this program of research concerning "judgment under uncertainty."
Such cognitive limitations may influence both the practice and the reporting of Bayesian analyses in ecology. First, when single-event probabilities are elicited from experts as input to a Bayesian analysis, the analyst must understand and correct any biases that may result from the expert's cognitive processes. Second, when writing a report, the Bayesian analyst must be aware of difficulties that a reader may experience with single-event probabilities as he strives to follow the logic of the analysis, retain the conclusions, and apply them elsewhere. Finally, because even experts often err when reasoning about single-event probabilities, the analyst may need to check carefully that he has set up and interpreted the analysis correctly.
Why are single-event probabilities hard for people to process?
In cognitive science, two schools of thought have developed to explain people's difficulties with single-event probabilities. The first school, based on the approach of Tversky and Kahneman (1974), assumes that each type of error in probabilistic reasoning represents an inherent limitation of human cognitive abilities. The human brain is seen as incapable of the complexities of accurate judgment about uncertainty. Instead, the mind depends on arbitrary heuristics or rules of thumb, producing flawed judgments and decisions. In the words of Stephen J. Gould (1992: 469), "Tversky and Kahneman argue, correctly, I think, that our minds are not built (for whatever reason) to work by the rules of probability." Although the cognitive errors resulting from these heuristics occur reliably in a variety of settings, most of this research has required subjects to reason about problems involving decimal estimates of single-event probabilities. The researchers suggest empirical methods that seem to counteract the errors in some situations, but they do not fit the cognitive inadequacies into any broad predictive or explanatory model.
The second school, based on the approach of Gigerenzer and Hoffrage (1995) and Cosmides and Tooby (1996) proposes the following arguments, based on evolutionary assumptions:
1) The mind includes structures that evolved to help preliterate people reason adaptively about situations commonly encountered across human evolutionary history, including making judgments under uncertainty.
2) Natural selection is unlikely to have produced a grossly inadequate mechanism for this purpose.
3) Cognitive structures designed to reason about probabilities will include both input mechanisms, which pick up information about stochastic events in the environment, and well-defined algorithms for processing that information.
Given these assumptions, humans in experimental situations can be expected to reason well about uncertainties only if two requirements are met: (1) input must be in a format "expected" by the human data-gathering mechanism (similarly, a calculator "expects" inputs in decimal, not binary, numbers); and (2) the problem must be structured to activate the information-processing algorithm that solves the particular problem, usually from probability theory, intended by the experimenter (a calculator will not provide a square root if the "log" button is pressed.)
Gigerenzer and his colleagues argue that cognitive illusions are artifacts of presentation format. People make mistakes, not because their reasoning ability is flawed, but because traditional experiments fail to provide the right conditions for the mind to reason correctly. They may present information in an inappropriate format (namely, decimal probabilities), or they may activate an algorithm in the mind that is not designed to process probabilistic information in the way that the experimenter expects. I will discuss issues of input format and algorithms in detail.
Input: single-event probabilities vs. frequencies
At first glance, single-event probabilities and frequencies seem to be readily interchangeable. Scientists routinely use frequency information to estimate probabilities. In a life table, for example, the decimal probability that a given individual will die in a future time period proceeds from counts of individuals surviving from one time period to the next. However, there are profound differences between the concepts (Gigerenzer 1994).
A frequency is a count of individuals or cases possessing some specific attribute, within a well-defined "reference class": a larger group of interest, including cases that do not possess the attribute in question. For example, we might describe a reference class: "Consider 100 populations of Spectacled Eiders nesting in eastern arctic Russia with current populations <500." Then we count the cases possessing a specific attribute: "Forty-six will become extinct in the next 10 years." Because of its dependence on the delimitation of the reference class, a frequency inevitably involves both verbal and quantitative information.
In contrast, a single-event probability quantifies the likelihood of a single event or expression of a hypothesis, expressed as a decimal number between 0 and 1.0. For example, the single-event probability that a particular population of Spectacled Eiders will become extinct in the next 10 years may be reported simply as "0.46." The single population in question might be a member of infinitely many reference classes (e.g., the class of populations in eastern arctic Russia, the class with current population <500, the class experiencing DDT intake of >500 micrograms per year, the class for which hunting is prohibited, and so on), but the decimal probability carries no information about the reference class of interest or appropriate limits of generalization. It applies only to the individual case.
Frequencies and single-event probabilities differ mathematically. Statisticians manipulate probabilities mathematically through the calculus of probability theory, which originated in the study of games of chance and is typically taught late in mathematical education. Frequencies, in contrast, map onto elementary set theory, an exercise in classification and counting that young children easily grasp (Dehaene 1997).
The skills involved with frequency processing appear to have a long evolutionary history. Experiments show that people, from an early age, readily classify objects and events (Cosmides and Tooby 1996) and track their frequencies over time and space unconsciously and accurately (Hasher and Zacks 1979, Brase et al. 1998). Many nonhuman animals appear to possess similar skills, enabling them to adjust their behavior adaptively to variable aspects of their environments (Cosmides and Tooby 1996, Dehaene 1997, Brase et al. 1998). In contrast, there is no reason to suppose a long evolutionary history of skill with single-event probabilities. Evidence from many nonindustrialized societies suggests that our hominid ancestors were not literate and probably possessed only rudimentary counting skills (Cosmides and Tooby 1996, Dehaene 1997). Considering these differences, it is not surprising that converting probabilities into frequency format tends to improve their intuitive clarity for most people.
Frequency format in action: Marbled Murrelets revisited.
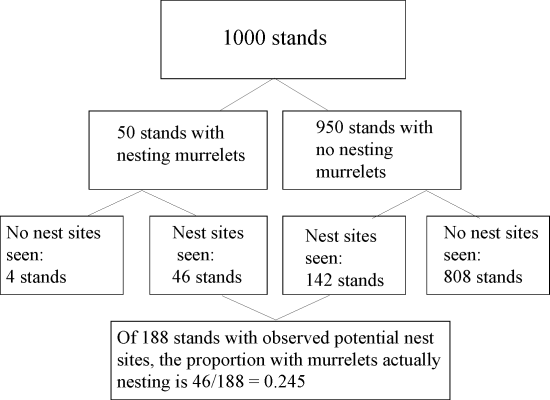
Most people, including scientists familiar with single-event probabilities, find even simple Bayesian problems, like the Marbled Murrelet example presented previously, difficult to formulate and solve correctly using decimal probabilities (see Bayesian and classical analysis: an example). In contrast, when the same data are organized as frequencies, the Bayesian problem becomes easier for many people (Gigerenzer and Hoffrage 1995). They find that they can follow the reasoning more readily because they can picture the reference classes and their subsets (Fig. 1).
Fig. 1. Frequency-format solution to Bayes' theorem for two hypotheses. Presentation of the data in frequency format seems to encourage mental imagery and facilitate estimation of the correct answer.
|
Algorithms: Subjective concepts related to probability
For most ecologists and statisticians, the word "probability" seems to have a clear meaning. However, cognitive scientists recognize that its subjective meaning can vary, depending on context (Jardine and Hrudey 1997). Teigen (1994) classified several ideas associated with probability and uncertainty (Table 3). Each of the subjective concepts implies its own calculus of "probability" and each seems to be processed by a different cognitive mechanism (Teigen 1994). It is important for Bayesian analysts to realize which idea they are activating when they refer to "probability" in a paper or ask an expert for a probability estimate.
Table 3. Classification of subjective concepts associated with probability (adapted from Teigen 1994).
|
Chance (Teigen 1994) probability refers to independent stochastic events external to the observer, such as coin tosses, measurement error in ecological variables, or the survival of an individual over a time unit. Mathematically, these events are analyzed by probability theory. If an analyst wants people to reason intuitively about probabilities in a way that corresponds to probability theory, he needs to activate this concept in their minds.
Tendency probability describes probabilities as propensities or dispositions of phenomena external to the viewer. For example, an ecologist might say that a Vancouver Island marmot's appearance below 500 m elevation is "improbable", meaning that the species is not disposed to live at that elevation. Subjectively, people tend to interpret tendency probabilities as attributes or properties of particular outcomes, leading them to estimate the probability of an outcome based on how "easily" it could occur. For example, many people feel uncomfortable standing near a precipice; subjectively, they assess a high probability of falling because a fall could "easily" happen, even though their position is secure, in reality. Similarly, in an ecological context, if it seems that extinction could "easily" occur or that the population in question has a "tendency" to become extinct, the subjective probability assigned to this outcome may exceed the stochastic (Chance) extinction probability.
Knowledge probability applies to the range of hypotheses under consideration and how confidence should be allocated among them. This interpretation of probability is familiar in applied ecology, as in all science, whenever researchers attempt to generate an exhaustive list of mutually exclusive hypotheses. A hypothesis that hasn't been thought of automatically receives a subjective knowledge probability of zero, even though it may be the correct explanation, in reality. For example, forest managers use an indicator of growth potential, the site index, in timber supply projections. For decades, they have considered standard methods for estimating the site index to be reliable. Now, however, evidence suggests that site indexes have been underestimated by 30 - 40% for some forest types in British Columbia (Pedersen 1997), so harvest projections now include an entirely new range of productivity estimates. Previously, those estimates would have been assigned a probability of zero.
Confidence probability refers to the degree of belief that a person has in a particular hypothesis. For example, she might decide to leave her jacket at home, based on her degree of confidence that the weather will be warm. Similarly, a fisheries manager might decide to open a hatchery, based on his confidence that survival to adulthood is not density dependent. Confidence probability is essentially subjective: internal to the observer, a characteristic that differentiates it strongly from chance probability.
Confidence probability is especially important for this discussion. The central assumption of Bayesian analysis is that probability should be interpreted subjectively as confidence or degree of belief in a hypothesis (Morgan and Henrion 1990: 49). Nonetheless, Bayesian analysis uses the mathematics of chance probability (probability theory) to manipulate these subjective probabilities. It is reasonable to question whether quantities derived from the subjective concept, confidence, can reasonably be processed by the same calculus as quantities based on chance probability. Indeed, experiments show that probability theory is poor at predicting people's confidence in their own judgments under uncertainty (Gigerenzer et al. 1991).
Control probability describes the degree to which the assessed probability of an event depends not only on its own stochastic characteristics, but also on what the assessor does to influence the event, regardless of the efficacy of his actions. For example, many people feel safer (i.e., they assess a lower subjective probability of an accident) as a driver than as a passenger in a car. In conservation ecology and resource management, this concept may cause problems when managers, who exert control over a resource, estimate probabilities on hypotheses concerning that resource.
Plausibility probability ought, perhaps, to have little relevance in scientific contexts, but even a scientific presentation is more likely to be believed (i.e., assigned a high subjective probability) if it tells a good story. Lively discussion, description of personal experience, clever catch-phrases, and skillful marshaling of supporting information are all elements of story-telling that may play into the hypothesized algorithms for plausibility in scientific communication. For example, the tactics of talented writers such as Richard Dawkins (1976) help to convince readers of the plausibility of their arguments.
These variants of subjective probability present a challenge to the ecologist who elicits probability estimates from experts or wishes his audience to follow an analysis of single-event probabilities. The same pattern of information can influence subjective estimates of "probability" in opposite directions when the data are processed by different cognitive algorithms. For example, it is possible to assign a high knowledge probability to a hypothesis because all other known alternatives have been ruled out, but still assign it a low confidence probability because there is little evidence in its favor.
Specific cognitive pitfalls of concern to ecological Bayesian analysts
In the next sections, I will examine three well-known cognitive illusions and their relevance to Bayesian analyses in ecology. In each case, I will show how appropriate input format and activation of the intended algorithm (chance) can improve people's intuitive ability to process probabilities.
Overestimation of single-event probabilities.
Probability theory demands that an exhaustive set of mutually exclusive single-event probabilities must sum to 1.0. This apparently obvious distributional constraint, however, is often violated in intuitive reasoning about single-event probabilities. For example, when asked to estimate single-event probabilities of individual stochastic outcomes (e.g., "What is the probability that a randomly selected male student at this university will be between 175 and 180 cm tall?"), subjects tend to overestimate each probability, and the sum of their estimates over the whole range of outcomes often greatly exceeds 1.0 (Teigen 1974b). In other experiments, subjects tend not to revise the probabilities that they assign to a set of hypotheses when the set is enlarged. For example, when subjects assign probabilities of guilt to a list of suspects for a fictional murder, suspects who could "easily" have committed the murder are assigned the same high probabilities, regardless of the number of other suspects that are introduced (Teigen 1983, Robinson and Hastie 1985, Teigen 1988).In an ecological context, overestimation can be especially troublesome where probability estimates from different experts must be combined. For example, a manager might ask a fire expert, an entomologist, and a meteorologist to estimate the probability that a stand of trees will be destroyed in the next 50 years by fire, insects, or windthrow, respectively. If each of these single estimates is overestimated, the total probability for the stand's destruction in the time period could be seriously biased upward.
Teigen (1994) attributes this cognitive bias to activation of the algorithm for tendency, under which assessed probability is an attribute of an individual outcome or hypothesis. As such, it is not constrained by the set of outcomes under consideration. Subjectively, probabilities in this context seem to be treated as though on an unbounded ordinal scale; the total can increase without limit as more outcomes are added to the set (Robinson and Hastie 1985). In contrast, probability theory assumes that single-event probabilities occupy a bounded ratio scale (0 - 1.0).
The lack of intuition about distributional constraints and the apparent mismatch of scales should be a concern for ecologists using expert elicitation. It affects both accuracy of individual estimates and coherence of the set of estimates (i.e., their agreement with probability theory). Expert elicitation should involve discussion and ad hoc correction of coherence among the estimates (Morgan and Henrion 1990, Ferrell 1994), but possible distortions produced by this practice have not been studied (Ferrell 1994). Neither exposure to basic probability distributions nor training at specific aspects of probability estimation has generally improved either coherence or accuracy in expert elicitation (Teigen 1974b, Robinson and Hastie 1985, Ferrell 1994).
Single-event probabilities differ crucially from most other variables in ecology because of distributional constraints. Ordinary variables can be considered attributes of the entity to which they apply, e.g., "the population has a density of 100 individuals/km2." Such variables can, with due care, be taken out of their original context and used for comparison or in an appropriate model. In contrast, although they superficially resemble other scientific data, probabilities from Bayesian analyses cannot be used in another context. A single-event probability estimate adjusted to fit coherently into one set of hypotheses or range of parameter values is not an attribute of the hypothesis to which it is attached. You cannot say that a hypothesis or outcome Y has single-event probability X, because the probability will change in any other context involving even a slightly different set of hypotheses or range of parameter values. For example, suppose a Bayesian analyst considered two population models, one assuming two age classes and another with three age classes. He might assign them probabilities of 0.45 and 0.55, respectively. If he added a third model including four age classes to the analysis, the original probabilities would no longer be valid. The probabilities do not "belong" to the models. These critical constraints may be obscured if a chance probability is interpreted subjectively as tendency.
Correcting overestimation.
Fortunately, experimental evidence suggests that overestimation of probability estimates is reduced by reporting or eliciting them as frequencies. The frequency format apparently causes people to process the information more like chance probabilities, resulting in a dramatic improvement in both accuracy and coherence (Teigen 1974a, Gigerenzer and Hoffrage 1995).Surprisingly, although many elaborate, ad hoc strategies for improving probability estimates exist (Morgan and Henrion 1990, Ferrell 1994, Chaloner 1996), they do not usually include the use of frequency format. Frequency format in expert elicitation deserves evaluation as a simple means of combating biases. For example, compare the following questions that might be addressed to an expert.
Because of the concrete nature of the latter approach, assessors are more likely to be aware if the total of their estimates exceeds 100. Activating mental imagery seems to be more effective than abstract presentations in mobilizing an expert's experience (Brunner et al. 1987).
The frequency format increases people's intuitive ease with probabilistic information
because it converts the mathematics into simple operations of set theory (Gigerenzer and Hoffrage 1995, Cosmides and Tooby 1996). In the previous example, the expert who provides "probabilities" for ranges of r must develop a mental probability density function and then integrate it over each range. In contrast, when he estimates the "number of populations out of 100" exhibiting r within each range, he need only divide the imagined set of 100 similar populations into three subsets and estimate the number of populations in each.
Furthermore, reporting the probability of a hypothesis as a frequency may help analysts to avoid the temptation to apply estimates inappropriately to new contexts. This is because we define a frequency only with respect to a specified reference group, e.g., Spectacled Eider populations nesting in eastern arctic Russia. Unlike a single-event probability misinterpreted as tendency, the frequency (the size of the subset within the reference class) applies to the subset, rather than to any individual case within the subset.
Finally, Bayesian analysts stress the advantage of being able to calculate probability density functions over continuous variables. However, the analyst must divide continuous variables into discrete ranges if he is to discuss the results in ordinary language, express them as hypotheses, or use them as "states of nature" in a decision analysis. For example, Taylor et al. (1996) divided
the continuous variable r (population growth rate) into three discrete ranges for use in a Bayesian decision analysis. Because it requires definition of a reference class and its subsets, the frequency format automatically encourages analysts to find meaningful divisions for continuous variables over which Bayesian probabilities have been calculated.
Despite the simplicity of the mathematics involved, the "conjunction fallacy" is perhaps the most familiar and pervasive of cognitive illusions. It occurs when people estimate a higher probability for two hypotheses in conjunction than for either hypothesis alone. The "Linda problem" described previously is a good example.
Teigen (1994) suggests that the conjunction fallacy results from the operation of the cognitive algorithm that processes subjective probabilities in terms of plausibility (Table 3). A story generally becomes more believable (and thus is assigned a higher subjective probability) as more details are added, even though each detail would constitute a separate hypothesis to be treated in conjunction if the story were an exercise in chance probability.
In ecology, the conjunction fallacy is a concern whenever people must estimate or understand the probability of an event that depends on a series of preceding uncertain events (Ferrell 1994). For example, the occurrence of a forest fire depends upon the forest reaching a threshold humidity level, a source of ignition, and a minimum wind speed within a specified area and time. If an expert estimates a probability of 0.1 for the independent occurrence of each contributing factor,
then his estimated probability of a fire should be no greater than 0.001. However, if the expert were to imagine all three factors together in circumstances that made the subjective plausibility algorithm active, he might judge a fire to be highly probable. It is necessary to structure elicitation interviews carefully to avoid this sort of confusion.
Intuitive difficulties with conjunction are also a consideration when expert elicitation or a Bayesian analysis involves a hypothesis or model plus one or more uncertain parameters. The probability of a model is the product of (1) the probability of the model's structure and (2) the probabilities of all of its assumptions. The product of many probabilities generally will be smaller than the product of fewer probabilities. Nonetheless, where several models are being compared, the conjunction fallacy may cause a model or hypothesis that specifies much detail (assumed parameter values) to be judged more probable than either a more general hypothesis within which it is nested, or a structurally different model with fewer assumptions. For example, the Chief Forester of British Columbia compared a series of models that predict long-term harvest level projections (Pedersen 1997). The models included progressively more silvicultural interventions and ecosystem management activities. Pedersen (1997) presented
a long list of factors assumed to influence harvest projections, as evidence of the validity of the most complex model. He concluded that its projections would be a good basis for management decisions. However, audience members might be drawn into the conjunction fallacy if they were reassured by the thought "That model must be good. It looks like they have thought of everything." Probability theory suggests that the many assumptions should provoke skepticism, rather than reassurance, about the complex model. The model is true only if all of its assumptions are simultaneously true.
Furthermore, because conjunction violations are difficult to detect intuitively, Bayesian analyses calculating probabilities of complex models can be hard for analysts to set up correctly and for readers to understand and evaluate. For example, Walters and Ludwig (1994) presented a Bayesian analysis of population parameters for a harvested fish population. Conjoint relationships between the model and its assumed parameters are so complex that their analysis is difficult for even sophisticated readers to grasp. Similarly, Sainsbury (1988, 1991) used Bayesian analysis to estimate probabilities for four structurally different models of population interactions proposed to explain the dynamics of a multispecies fish community in Australia. He analyzed each model in conjunction with one set of parameter values (Sainsbury et al. 1997). He constrained the posterior probabilities for the four model-parameter set conjunctions to add to 1.0, despite the fact that each model could reasonably have been analyzed in conjunction with many other parameter sets. If the other combinations had been admitted to the analysis, the posterior probabilities for the four chosen model-parameter set conjunctions would have been much smaller than those reported. An unwary reader might place high confidence in the "model" with a reported posterior probability of 0.62 when, in fact, the probability of a single conjunction had been inflated to represent the model as a whole.
This strategy should be easy to apply in expert elicitation. A series of questions like the following is vulnerable to conjunction violations: "What is the probability that the population of mountain goats in Cathedral Park, British Columbia, is declining? What is the probability that it is declining and disappearing from marginal habitats?" In a frequency format, it might read: "Imagine 100 populations of mountain goats above 1500 m elevation in southern British Columbia. How many are declining? Of those, how many are declining and disappearing from marginal habitat?"
Bayesian analysts could develop consistent standards for clear reporting of conjoint probabilities on models and their parameters. It would probably prove helpful for authors to articulate their results in frequency terms, because the specification of the reference class automatically exposes the conjunctions between parameters and models. For example, a comparison of Tables 2 and 4
shows how Pascual and Hilborn's (1995: 475) posterior probabilities could
be translated into frequency format.
beta
Marginal total = 10
Marginal total = 81
Marginal total = 9
The concrete presentation in Table 4 confers several advantages. First, the choice of a reference class size that people can visualize (usually between 10 and 1000) sets a reasonable limit on the inclusion of infinitesimal probabilities. The choice of 100 as the reference class size in Table 4 gives the frequency estimates two significant figures, a reasonable degree of resolution for most
ecological analyses. The original thirteen rows of data reported to five significant figures by Pascual and Hilborn boil down to just seven rows containing non-zero frequencies.
Second, frequencies encourage critical examination of the conjoint results. Consider the left column of Table 4: cases with a "low" slope for the recruitment function. In all cases but one in this group, the intercept beta is between 0.160 and 0.174. Does this degree of uniformity correspond with the reader's own intuition? It is much more difficult to perceive and evaluate this result in the original table.
Finally, the exercise of reinterpreting results in frequency format could indicate to authors whether or not their results will be successful "memes." If the analysis is so abstract and complex that its results cannot be restated as frequencies within clear reference classes, authors should suspect that errors may go undetected and few readers will understand or use the conclusions.
This cognitive illusion has obvious relevance when resource managers are asked to make probability judgments about outcomes for which they are held responsible. For example, Wolfson et al. (1996: Fig. 1) present a graph of prior probabilities for varying pollution levels estimated by Environmental Protection Agency officials. The probabilities fall off steeply just at the mandated threshold.
These results suggest that, in situations where the illusion of control might cause bias, the analyst should encourage respondents to visualize management decisions replicated many times. Compare possible questions addressed to a planner who is designing a forest ecosystem network to maintain biodiversity within a watershed.
Probability format: "What is the probability that this watershed, for which you have planned a forest ecosystem network, will retain all 14 species of passerines 40 years from now?"
Frequency format: "Picture 100 watersheds like this one. For each, you have planned a similar forest ecosystem network. How many will retain all 14 species of passerines 40 years from now?"
The frequency version makes it easier to imagine that the landscape management plan might produce variable results. The effects of doing so may vary, depending on whether the repeated trials are visualized as happening concurrently or sequentially. Research is needed in this area.
When designing graphic displays, Bayesian analysts would benefit from understanding aspects of human visual perception. A Bayesian analysis often generates probability density functions or cumulative probability distributions over continuous parameters (e.g., Crome et al. 1996, Ludwig 1996). However, unless the intended audience has been trained to interpret these graphs, they are more likely to feel comfortable with simple histograms (Ibrekk and Morgan 1987, Edwards 1996). Considering how important frequency format is to accurate processing of probabilistic information, the preference for histograms is not surprising, because they convert probabilities into frequencies. Wilkinson et al. (1992), Morgan and Henrion (1990), and Vose (1996) discuss additional perceptual considerations for graphic displays of data. Despite the cliché "a picture is worth a thousand words", the message of a successful graph should be expressible in ordinary language. Only then can readers remember the information and convey it informally to their colleagues or to interested people who are not experts.
The small but growing number of Bayesian analyses in conservation and applied ecology brings up an unexpected new challenge: the need for expertise in cognitive psychology. In particular, ecological Bayesian analyses involving elicited probability estimates are, unavoidably, exercises in cognitive and social science. To select techniques for probability elicitation, Bayesian analysts will have to grapple with the controversies in cognitive psychology concerning judgment under uncertainty (Morgan and Henrion 1990, Ferrell 1994, Gigerenzer and Hoffrage 1995). To rigorously evaluate the validity and reliability of these methods, editors and reviewers will also have to become familiar with issues in cognitive science.
Furthermore, ecologists interested in the acceptance of Bayesian methods may find it useful to consider the factors that seem to influence the spread of other ideas and practices within the scientific community. Parallels with the ongoing effort to establish the practice of statistical power analysis (Sedlmeier and Gigerenzer 1989, Peterman 1990) suggest that both university teachers and journal editors will need to assume a leadership role. They may need to encourage (1) consistent methods for producing verbal summaries from quantitative data, (2) translation of single-event probabilities into frequencies with careful definition of reference classes, (3) attention to different cognitive interpretations of probability concepts, and (4) conventions for graphic displays. At times, these strategies may seem simple-minded when they replace recondite abstractions with concrete images and operations. The goal of this exercise should be to ensure that Bayesian analyses and their results will become successful memes, assimilated, recalled, recognized, and utilized accurately by conservation ecologists and resource managers.
Responses to this article are invited. If accepted
for publication, your response will be hyperlinked
to the article. To submit a comment, follow
this link. To read comments already accepted,
follow this link.
This project has been supported by a grant from the Forest Renewal British Columbia fund. Randall Peterman, Brian Pyper, Ken Lertzman, and two anonymous reviewers made encouraging and helpful suggestions for improving the manuscript.
Adkison, M., and R. M. Peterman. 1996. Results of Bayesian methods depend on details of implementation: an example of estimating salmon escapement goals. Fisheries Research 25:155-170.
Ayton, P., and G. Wright. 1994. Subjective probability: what should we believe? Pages 163-184 in G. Wright and P. Ayton, editors. Subjective probability. Wiley, New York, New York, USA.
Berry, D. A., and D. K. Stangl. 1996. Bayesian methods in health-related research. Pages 3-66 in D. Berry and D. Stangl, editors. Case studies in Bayesian biostatistics. Marcel Dekker, New York, New York, USA.
Bjornstad, D. J., and J. R. Kahn. 1996. Structuring a research agenda to estimate environmental values. Pages 263-274 in D. J. Bjornstad and J. R. Kahn, editors. The contingent valuation of environmental resources. Edward Elgar, Cheltenham, UK.
Box, G. E. P., and G. C. Tiao. 1973. Bayesian inference in statistical analysis. Addison-Wesley, Reading, Massachusetts, USA.
Boyd, R., and P. Richerson. 1985. Culture and the evolutionary process. University of Chicago Press, Chicago, Illinois, USA.
Brase, G. L., L. Cosmides, and J. Tooby. 1998. Individuation, counting, and statistical inference: the role of frequency and whole-object representations in judgment under uncertainty. Journal of Experimental Psychology: General 127(1):3-21.
Brunner, R. D., and T. W. Clark. 1997. A practice-based approach to ecosystem
management. Conservation Biology 11(1):48-56.
Brunner, R. D., J. S. Fitch, J. Grassia, L. Kathlene, and K. R. Hammond. 1987. Improving data utilization: the case-wise alternative. Policy Sciences 20:365-394.
Burton, R. J., A. C. Balisky, L. P. Coward, S. G. Cumming, and D. D. Kneeshaw. 1992. The value of managing for biodiversity. Forestry Chronicle 68:225-234.
Cavalli-Sforza, L. L., and M. W. Feldman. 1981. Cultural transmission and evolution:
a quantitative approach. Princeton University Press, Princeton, New Jersey, USA.
Chaloner, K. M. 1996. The elicitation of prior distributions. Pages 141-156 in D. Berry and D. Stangl, editors. Case studies in Bayesian biostatistics. Marcel Dekker, New York, New York, USA.
Clark, T. W. 1993. Creating and using knowledge for species and ecosystem conservation:
science, organizations, and policy. Perspectives in Biology and Medicine 36(3):497-525.
Cooper, H. M., and L. V. Hedges. 1994. The handbook of research synthesis.
Russell Sage Foundation, New York, New York, USA.
Cosmides, L., and J. Tooby. 1996. Are humans good intuitive statisticians after all? Rethinking some conclusions from the literature on judgment under uncertainty. Cognition 58:1-73.
Crome, F. H. J., M. R. Thomas, and L. A. Moore. 1996. A novel Bayesian approach to assessing impacts of rain forest logging. Ecological Applications 6(4):1104-1123.
Dawkins, R. 1976. The selfish gene. Oxford University Press, New York, New York, USA.
Dehaene, S. 1997. The number sense: how the mind creates mathematics. Oxford University Press, Oxford, UK.
Dennis, B. 1996. Discussion: Should ecologists become Bayesians? Ecological
Applications 6(4):1095-1103.
Edwards, D. 1996. Comment: The first data analysis should be journalistic.
Ecological Applications 6(4):1090-1094.
Ellison, A. M. 1996. An introduction to Bayesian inference for ecological research
and environmental decision-making. Ecological Applications 6:1036-1046.
Fairweather, P. B. 1991. Statistical power and design requirements for environmental
monitoring. Australian Journal of Marine and Freshwater Research 42:555-567.
Ferrell, W. R. 1994. Discrete subjective probabilities and decision analysis:
elicitation, calibration, and combination. Pages 411-451 in G. Wright and
P. Ayton, editors. Subjective probability. Wiley, New York, New York, USA.
Garrod, G. D. 1997. The non-use benefits of enhancing forest biodiversity: a contingent ranking study. Ecological Economics 21:45-61.
Gigerenzer, G. 1991. From tools to theories: a heuristic of discovery in cognitive
psychology. Psychological Review 98(2):254-267.
_______ . 1994. Why the distinction between single-event probabilities and frequencies is relevant for psychology (and vice versa). Pages 129-162 in G. Wright and P. Ayton, editors. Subjective probability. Wiley, New York, New York, USA.
Gigerenzer, G., and R. Hertwig. 1997. The "conjunction fallacy" revisited: how intelligent inferences look like reasoning errors. MS submitted for publication.
Gigerenzer, G., and U. Hoffrage. 1995. How to improve Bayesian reasoning without
instruction: frequency formats. Psychological Review 102(4):684-704.
Gigerenzer, G., U. Hoffrage, and H. Kleinboelting. 1991. Probabilistic mental models: a Brunswikian theory of confidence. Psychological Review 98:506-528.
Gigerenzer, G., and D. J. Murray. 1987. Cognition as intuitive statistics. Erlbaum, Hillsdale, New Jersey, USA.
Gould, S. J. 1992. Bully for Brontosaurus: further reflections in natural history. Penguin, London, UK.
Hasher, L., and R. T. Zacks. 1979. Automatic and effortful processes in memory.
Journal of Experimental Psychology: General 108:356-388.
Hilborn, R., E. K. Pikitch, and M. K. McAllister. 1994. A Bayesian estimation and decision analysis for an age-structured model using biomass survey data. Fisheries Research 1719:17-30.
Howson, C., and P. Urbach. 1989. Scientific reasoning: the Bayesian approach. Open Court, LaSalle, Illinois, USA.
Ibrekk, H., and M. G. Morgan. 1987. Graphical communication of uncertain quantities
to non-technical people. Risk Analysis 7(4):519-529.
Jardine, C. G., and S. E. Hrudey. 1997. Mixed messages in risk communication.
Risk Analysis 17(4):489-498.
Kahneman, D., and A. Tversky. 1979. Prospect theory: an analysis of decision
under risk. Econometrica 47:263-291.
Keren, G. 1991. Additional tests of utility theory under unique and repeated
conditions. Journal of Behavioral Decision Making 4:297-304.
Keren, G., and W. A. Wagenaar. 1987. Violation of utility theory in unique
and repeated gambles. Journal of Experimental Psychology: Learning, Memory,
and Cognition 13(3):387-391.
Knetsch, J. L. 1990. Environmental policy implications of disparities between
willingness to pay and compensation demanded measures of values. Journal of
Environmental Economics and Management 18:227-237.
Koehler, J. J., B. J. Gibbs, and R. M. Hogarth. 1994. Shattering the illusion
of control: multi-shot versus single-shot gambles. Journal of Behavioral Decision
Making 7:183-191.
Langer, E. J. 1975. The illusion of control. Journal of Personality and Social
Psychology 32:311-328.
Lee, P. M. 1989. Bayesian statistics: an introduction. Oxford University Press, New York, New York, USA.
Ludwig, D. 1996. Uncertainty and the assessment of extinction probabilities.
Ecological Applications 6(4):1067-1076.
Maguire, L. A. 1986. Using decision analysis to manage endangered species populations.
Journal of Environmental Management 22:345-360.
_______ . 1988. Decision analysis: an integrated approach to ecosystem exploitation and rehabilitation decisions. Pages 106-121 in J. Cairns, editor. Rehabilitating damaged ecosystems. Volume 2. CRC Press, Boca Raton, Florida, USA.
Maguire, L. A., and L. G. Boiney. 1994. Resolving environmental disputes: a framework incorporating decision analysis and dispute resolution techniques. Journal of Environmental Management 42:31-48.
Mayo, D. G. 1996. Error and the growth of experimental knowledge. University of Chicago Press, Chicago, Illinois, USA.
Meffe, G. K., and S. Viederman. 1995. Combining science and policy in conservation
biology. Wildlife Society Bulletin 23(3):327-332.
Morgan, M. G., and M. Henrion. 1990. Uncertainty: a guide to dealing with uncertainty
in quantitative risk and policy analysis. Cambridge University Press, Cambridge, UK.
Parkhurst, D. F. 1984. Decision analysis for toxic waste releases. Journal of Environmental Management 18:105-130.
Parson, E. A., and W. C. Clark. 1995. Sustainable development as social learning: theoretical perspectives and practical challenges for the design of a research program. Pages 429-459 in L. H. Gunderson, C. S. Holling, and S. S. Light, editors. Barriers and bridges to the renewal of ecosystems and institutions. Columbia University Press, New York, New York, USA.
Pascual, M. A., and R. Hilborn. 1995. Conservation of harvested population in fluctuating environments: the case of the Serengeti wildebeest. Journal of Applied Ecology 32:468-480.
Pedersen, L. 1997. The truth is out there. Annual Convention of the Northern
Forest Products Association. Prince George, British Columbia, Canada.
Peterman, R. M. 1990. Statistical power analysis can improve fisheries research
and management. Canadian Journal of Fisheries and Aquatic Science 47:2-15.
Press, S. J. 1989. Bayesian statistics: principles, models, and applications.
Wiley, Toronto, Canada.
Raiffa, H. 1968. Decision analysis: introductory lectures on choices under uncertainty. Don Mills, Ontario, Canada.
Robinson, L. B., and R. Hastie. 1985. Revision of beliefs when a hypothesis is eliminated from consideration. Journal of Experimental Psychology: Human Perception and Performance 11(4):443-456.
Sainsbury, K. J. 1988. The ecological basis of multispecies fisheries, and
management of a demersal fishery in tropical Australia. Pages 349-382 in
J. A. Gulland, editor. Fish population dynamics. Wiley, New York, New York, USA.
_______ .1991. Application of an experimental approach to management of a tropical multispecies fishery with highly uncertain dynamics. ICES Marine Science Symposium 193:301-320.
Sainsbury, K. J., R. A. Campbell, R. Lindholm, and A. W. Whitelaw. 1997. Experimental
management of an Australian multispecies fishery: examining the possibility of trawl-induced habitat modification. Pages 105-112 in E. L. Pikitch, D. D. Huppert, and M. P. Sissenwine, editors. Global trends: fisheries management. Volume 20. American Fisheries Society, Bethesda, Maryland, USA.
Sedlmeier, P., and G. Gigerenzer. 1989. Do studies of statistical power have an effect on the power of studies? Psychological Bulletin 105(2):309-316.
Shadish, W. R., Jr. 1989. The perception and evaluation of quality in science. Pages 383 - 428 in B. Gholson, W. R. Shadish, Jr., R. A. Neimeyer, and A. C. Houts, editors. Psychology of science: contributions to metascience. Cambridge University Press, Cambridge, UK.
Siegrist, M. 1997. Communicating low risk magnitudes: incidence rates expressed
as frequency versus rates expressed as probability. Risk Analysis 17(4):507-510.
Stahl, G., D. Carlsson, and L. Bondesson. 1994. A method to determine optimal stand data acquisition policies. Forest Science 40(4):630-649.
Tanner, W. P. J., and J. A. Swets. 1954. A decision-making theory of visual detection. Psychological Review 61:401 - 409.
Taylor, B. L., P. R. Wade, R. A. Stehn, and J. F. Cochrane. 1996. A Bayesian
approach to classification criteria for Spectacled Eiders. Ecological Applications
6(4):1077-1089.
Teigen, K. H. 1974a. Overestimation of subjective probabilities.
_______ . 1974b. Subjective sampling distributions and the additivity of
estimates. Scandinavian Journal of Psychology 15:50-55.
_______ . 1983. Studies in subjective probability III. The unimportance of alternatives. Scandinavian Journal of Psychology 24:97-105.
_______ . 1988. When are low-probability events judged to be "probable"?
Effects of outcome-set characteristics on verbal probability judgments. Acta
Psychologica 67:157-174.
_______ . 1994. Variants of subjective probabilities: concepts, norms,
and biases. Pages 211-238in G. Wright and P. Ayton, editors. Subjective
probability. Wiley, New York, New York, USA.
Thompson, G. G. 1992. A Bayesian approach to management advice when stock-recruitment parameters are uncertain. Fishery Bulletin 90:561-573.
Tversky, A., and D. Kahneman. 1974. Judgment under uncertainty: heuristics
and biases. Science 185:1124-1131.
Underwood, A. J. 1990. Experiments in ecology and management: their logics,
functions, and interpretations. Australian Journal of Ecology 15:365-390.
Vose, D. 1996. Quantitative risk analysis: a guide to Monte Carlo simulation
modelling. John Wiley, Toronto, Canada.
Walters, C. J. 1986. Adaptive management of renewable resources. MacMillan, New York, New York, USA.
Walters, C. J., and D. Ludwig. 1994. Calculation of Bayes posterior probability
distributions for key population parameters. Canadian Journal of Fisheries and Aquatic Science 51:713-722.
Weeks, P., and J. M. Packard. 1997. Acceptance of scientific management by
natural resource-dependent communities. Conservation Biology 11(1):236-245.
Wilkinson, L., M. A. Hill, and E. Vang. 1992. Cognitive science and graphic
design. Pages 40-63 in SYSTAT: Graphics. Version 5.2 edition. Systat, Evanston, Illinois, USA.
Wolfson, L. J., J. B. Kadane, and M. J. Small. 1996. Bayesian environmental policy decisions: two case studies. Ecological Applications 6(4):1056-1066.
Zar, J. H. 1996. Biostatistical analysis. Prentice-Hall, Toronto, Canada.
What is the probability that it is between -0.05 and 0.0?
What is the probability that it is greater than 0.0?"
How many would exhibit r between -0.05 and 0.0?
How many would exhibit r greater than 0.0?"
Conjunction fallacy.
The idea of "conjunction" is central to probability
theory and seems intuitively obvious. Two hypotheses are "in conjunction" or "conjoint" if they are true at the same time. Probability theory states: Assuming A and B are independent hypotheses, P(A + B) = P(A) * P(B). Because probabilities are never greater than 1.0, their product will be less than or equal to the individual probabilities. In other words, it is harder for two things to be true at the same time than for one thing to be true.
Correcting conjunction violations.
As with the overestimation problem, the conjunction fallacy disappears when placed in a context of frequencies (Gigerenzer 1994, Gigerenzer and Hoffrage 1995). Most subjects, when asked "Out of 100 people like Linda, how many are bank tellers?" and "Out of 100 people like Linda, how many are bank tellers and active in the feminist movement?", correctly answer the latter with a smaller number. Frequency formats apparently help subjects to avoid the plausibility interpretation and generate estimates consistent with chance probability calculus (G. Gigerenzer and R. Hertwig, unpublished manuscript).
Table 4. Example of the frequency format, for comparison with Table 2, showing expected frequencies of populations exhibiting each category of the parameters (alpha and beta) that characterize the function relating recruitment to dry-season rainfall. Frequencies are based on 100 hypothetical populations of migratory Serengeti wildebeest with low levels of rinderpest, a food-limited, stable population size of ~ 1,200,000, and significant exposure to poaching.
Low
slope: alpha = 0.0 to 0.006
Medium
slope: alpha = 0.008 to 0.012
High
slope: alpha = 0.014 to 0.020
0.040
to 0.070
0
0
0
0.085
0
0
2
0.100
0
0
7
0.115
0
19
0
0.130
0
34
0
0.145
0
28
0
0.160
9
0
0
0.175
1
0
0
0.190
to 0.220
0
0
0
Illusion of control.
When presented with a purely stochastic situation,
people tend to overestimate the probability of a favorable outcome over which they feel they have control. The classic example is the demonstration by Langer (1975) that subjects valued a lottery ticket they selected themselves more highly than one given to them by the experimenter, even though they knew the expected value (real probability of winning times the prize) was the same for both tickets. Although it did not affect the outcome of the gamble, the act of choosing seemed to activate the hypothesized control probability algorithm, increasing the subjectively estimated probability of winning.
Correcting the illusion of control: repeated gambles.
The illusion of
control seems to be an artifact of framing the probability judgment as a one-shot gamble or single-event probability. Koehler et al. (1994) demonstrated that subjects given a false sense of control in a gamble, as in Langer's experiment, nonetheless provided accurate (chance) probability estimates when they were encouraged to consider repeated stochastic outcomes. This improvement in performance was sustained even when subjects were constrained to a single gamble, as long as they could visualize multiple stochastic outcomes before making their probability judgments.
Other relevant cognitive issues.
Cognitive distortions relevant to conservation ecology are not limited to reasoning about Bayesian analyses. They cause difficulties
with techniques for environmental economic analysis such as utility estimates (Kahneman and Tversky 1979) and contingent valuation (Knetsch 1990, Burton et al. 1992, Bjornstad and Kahn 1996, Garrod 1997). In both cases, frequency formats seem to be beneficial (Keren and Wagenaar 1987, Keren 1991, Siegrist 1997). Perceptions of risk and risk reversibility, important but problematic variables in ecological risk analysis, also seem to improve when subjects consider repeated outcomes (Keren and Wagenaar 1987, Keren 1991).
Acknowledgments
Address of Correspondent:
Judith L. Anderson
School of Resource and Environmental Management
Simon Fraser
University
Burnaby, British Columbia, Canada V5A 1S6
Phone: (604) 526-4722
Fax: (604) 291-4968
janderso@sfu.ca
*The copyright to this article passed from the Ecological Society of America to the Resilience Alliance on 1 January 2000.