|
|
|
Copyright © 1997 by The Resilience Alliance*
van Coller, L. 1997. Automated techniques for the qualitative analysis of ecological models: continuous models. Conservation Ecology [online]1(1): 5. Available from the Internet. URL: http://www.consecol.org/vol1/iss1/art5/
A version of this article in which text, figures, tables, and appendices are separate files may be found by following this link.
Research Automated Techniques for the Qualitative Analysis of Ecological Models: Continuous Models Lynn van Coller1
Department of Mathematics,University of British Columbia
- Abstract
- Introduction
- Ratio-Dependent Model
- Resilience
- Conclusion
- Acknowledgments
- Responses
- Literature Cited
KEY WORDS: bifurcation; computer analysis; dynamical systems; ecological models; qualitative analysis; ratio-dependent model; XPPAUT.
Caution: If your browser does not handle graphics, the mathematical models and all Greek characters will be unreadable in this online version. Please email the author to obtain a complete hard copy.
Most parameter values in nature are not known with certainty (Hadamard 1952, Frank 1978). It is also well known that different parameter values in a model can give rise to very different dynamics, such as stable equilibrium behavior, oscillatory behavior, or a decline to extinction. However, finding parameter combinations that give rise to these different dynamics is often a matter of trial and error and involves numerous simulations. The dynamical systems software provides an easier and more systematic way to do this.
In this paper, I substantiate this claim by using the software XPPAUT (Ermentrout 1994), which contains an interface to AUTO86 (Doedel 1981), to analyze three continuous ecological models of varying complexity. Appendix 5 contains a list of other packages that have capabilities similar to XPPAUT or AUTO86. In the main body of this paper, I consider only one of these models in detail. This model is a recent example from the controversial area of ratio-dependent modeling. It has three state variables that represent a plant, a herbivore, and a predator. In addition to highlighting some of the limitations of an isocline analysis in this three-dimensional setting, the analysis shows that the model is structurally unstable. Even small perturbations to the ratio-dependent terms alter the dynamics.
Appendix 4 discusses the application of the software to a system dynamics model that has 10 state variables and a large number of parameters. Analytical work done by hand and isocline analyses are of little use in such situations. Traditionally, computers have been used to obtain numerical solutions corresponding to a fixed parameter set and to implement sensitivity analyses. In Appendix 4 , I show how dynamical systems techniques can be used to increase our understanding of the relationships between different components in the model. In particular, bifurcation diagrams give more information than sensitivity analyses. These diagrams also highlight an incomplete relationship in the model and lead to an improvement in the formulation of the equations. Thus, the packages can help us to formulate more plausible models.
Because this paper is intended as an introduction to the application of dynamical systems techniques to ecological models, I include a number of appendices. Appendix 2 introduces some of the ideas and terminology and also provides a glossary of the terms used in the paper and appendices. Those readers unfamiliar with dynamical systems ideas may benefit from a quick reading of this appendix before continuing. A more comprehensive exposition, also specifically written for ecologists, can be found in Yodzis (1989). Another excellent introduction to nonlinear dynamics can be found in Strogatz (1994). Appendix 3 shows how the dynamical systems techniques can be applied to a fairly simple predator-prey model using XPPAUT. I show how I reproduced and improved on Bazykin's analytical results (Bazykin 1974) for the model. This appendix establishes some confidence in the reliability of the computer software.
I also discuss the topic of model resilience, a concept introduced by Holling (1973), to parameter and population perturbations.
I also claim that the technique used by Gutierrez et al. (1994) to study the model, namely isocline analysis (for technique and examples, see Edelstein-Keshet 1988), is unsuitable in this three-dimensional setting. This is discussed in detail in section 2.2.4. Although isocline analyses have been employed in many settings and with considerable success (Fitzhugh 1961, Rosenzweig and MacArthur 1963, Gilpin 1974, Hethcote 1976, Ludwig et al. 1978, Fairen and Velarde 1979, Murray 1981), in more complicated, higher dimensional models for which the categorization of variables as slow vs. fast is not possible, their application is limited. (If the state variables in a model vary on different time scales, it is often possible to approximate the system by a two-dimensional model representing either the slow or the fast dynamics. An isocline analysis can then be done using the reduced system.) An isocline analysis allows two variables, at most, to vary simultaneously. This means that, for the current model, one variable is held fixed, resulting in a partly static representation of the dynamics. However, the dynamical systems techniques allow all three state variables to vary simultaneously, thus permitting a more accurate analysis.
2.1 Model Equations
The basic model equations and a description of the parameters can be found in Appendix 1 . There are three equations describing the dynamics of a plant, a herbivore, and a predator. In Appendix 1 , I describe how I nondimensionalized the equations and introduced a small modification to the ratio-dependent terms. The resulting equations are as follows:
In the next section, I compare results from the original model, (ai = 0) with those from the modified equations (ai = 0.001). I chose this latter value for the ai's because it only affects the isocline configurations (see Appendix 1 ) at low values of the state variables, which is where the difficulties with the ratio-dependent model are encountered. I also investigate a few other values.
2.2 Model analysis
2.2.1 One-parameter studies
Gutierrez et al. (1994) did a partial qualitative analysis of the original model, but used different techniques (namely, isocline analysis), so it will be informative to compare some of the results. I chose dimensionless parameters with this in mind (see Appendix 1 ). Because one of the main conclusions in Gutierrez et al. (1994) concerns the relative efficacy of two parasitoids in controlling the cassava mealybug population, I begin by studying two parameters that affect the third trophic level, namely and
and
 . I then discuss some
parameters affecting the herbivore. Only a few examples are included
here. Results, together with possible biological interpretations, are
described in the next section.
. I then discuss some
parameters affecting the herbivore. Only a few examples are included
here. Results, together with possible biological interpretations, are
described in the next section.
2.2.2 Analysis of the predator parameters
The parameter can be thought of as the potential
predator biomass growth rate when prey are abundant, or as the
predator's conversion efficiency in the presence of abundant
prey. Note that the value of
can be thought of as the potential
predator biomass growth rate when prey are abundant, or as the
predator's conversion efficiency in the presence of abundant
prey. Note that the value of
 does not affect the isoclines. The
M3 zero isocline is given by
does not affect the isoclines. The
M3 zero isocline is given by
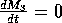 , and the solution of
this equation is independent of
, and the solution of
this equation is independent of
 (see equations
(1). Hence, an
isocline analysis similar to that done in Gutierrez et al. (1994)
would not give any insight into how this parameter influences the
behavior of the system.
(see equations
(1). Hence, an
isocline analysis similar to that done in Gutierrez et al. (1994)
would not give any insight into how this parameter influences the
behavior of the system.
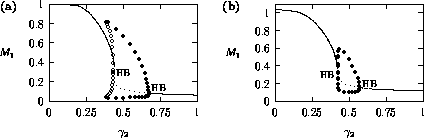
Bifurcation diagrams showing the effects of varying
 for both the original
and the modified model are shown in
Fig. 1
, with
M1 plotted on the y-axis. These
diagrams were obtained using AUTO through XPPAUT. In both Fig. 1
diagrams, the position of the equilibrium point does not vary with
for both the original
and the modified model are shown in
Fig. 1
, with
M1 plotted on the y-axis. These
diagrams were obtained using AUTO through XPPAUT. In both Fig. 1
diagrams, the position of the equilibrium point does not vary with
 , supporting the
previous observation that
, supporting the
previous observation that
 does not affect the isocline
configuration. However,
does not affect the isocline
configuration. However,
 does affect the stability of the
system. In both cases, the equilibrium point is unstable for very low
values of
does affect the stability of the
system. In both cases, the equilibrium point is unstable for very low
values of  (low
predator growth rate) and the stable attractor is a limit cycle for
these values. The original model gives an example of hard loss of
stability (see
Appendix
2) so that, for certain values of
(low
predator growth rate) and the stable attractor is a limit cycle for
these values. The original model gives an example of hard loss of
stability (see
Appendix
2) so that, for certain values of
 , there are two stable attractors,
a sink and a stable limit cycle (as in
Fig. 11
). The
initial values of the state variables determine which final state is
reached. Also, perturbations to the system may cause a rapid change
from one stable attractor to the other if the disturbance is
sufficiently large. For a very small range of
, there are two stable attractors,
a sink and a stable limit cycle (as in
Fig. 11
). The
initial values of the state variables determine which final state is
reached. Also, perturbations to the system may cause a rapid change
from one stable attractor to the other if the disturbance is
sufficiently large. For a very small range of
 values near the Hopf bifurcation
point HB in Fig. 1
a, there are two stable limit cycles. The range of
values is so small, however, that it is not of much biological
significance.
values near the Hopf bifurcation
point HB in Fig. 1
a, there are two stable limit cycles. The range of
values is so small, however, that it is not of much biological
significance.
FIGURE 1:
One-parameter bifurcation diagrams showing the effects of
varying  for (a) the original model and (b) the modified
model. The state variable
for (a) the original model and (b) the modified
model. The state variable 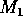 is plotted on the y-axes.
is plotted on the y-axes.
FIGURE 11:
Isoclines in the (a)  and (b)
and (b) 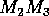 planes
for
planes
for 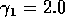 ,
, 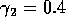 ,
, 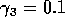 ,
,
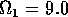 ,
, 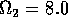 ,
, 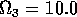 ,
,
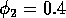 ,
, 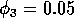 , and
, and 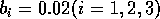 . Both
the stable equilibrium point and the limit cycle are shown.
. Both
the stable equilibrium point and the limit cycle are shown.
Analysis of the temporal dynamics of the system (using XPPAUT) for
different values of
 shows that larger values of
shows that larger values of
 decrease the time
taken to reach equilibrium. Increasing
decrease the time
taken to reach equilibrium. Increasing
 , the potential growth rate of the
predator, has a stabilizing influence on the system. This seems
biologically plausible, because higher values of
, the potential growth rate of the
predator, has a stabilizing influence on the system. This seems
biologically plausible, because higher values of
 suggest that the predator is better
adapted to controlling its prey. Interestingly, this trait does not
affect any of the equilibrium biomasses. The modified model has a
much smaller range of parameter values over which cycles occur, and
the amplitudes of these cycles are smaller than for the original model
(see Fig. 1
). Thus, even though the ai' s
have small values, they appear to have a stabilizing influence on the
dynamics.
suggest that the predator is better
adapted to controlling its prey. Interestingly, this trait does not
affect any of the equilibrium biomasses. The modified model has a
much smaller range of parameter values over which cycles occur, and
the amplitudes of these cycles are smaller than for the original model
(see Fig. 1
). Thus, even though the ai' s
have small values, they appear to have a stabilizing influence on the
dynamics.
 , the
availability (or nutritional value) of the herbivore to the predator,
also directly affects the predator. Bifurcation diagrams for the
original and modified models, respectively, are shown in
Fig. 2
and Fig. 3
. From these
figures, it can be seen that as
, the
availability (or nutritional value) of the herbivore to the predator,
also directly affects the predator. Bifurcation diagrams for the
original and modified models, respectively, are shown in
Fig. 2
and Fig. 3
. From these
figures, it can be seen that as
 increases, there is a general
increase in the M1 equilibrium value, or
limit cycle maximum. The larger
increases, there is a general
increase in the M1 equilibrium value, or
limit cycle maximum. The larger
 , the greater the availability of
the herbivore to the predator and the easier it is for the predator to
control the herbivore. Obviously, the lower the herbivore population,
the higher the plant equilibrium. As the M1
equilibrium value approaches the M1 carrying
capacity in the original model, a Hopf bifurcation (see Appendix 2
)
occurs at
, the greater the availability of
the herbivore to the predator and the easier it is for the predator to
control the herbivore. Obviously, the lower the herbivore population,
the higher the plant equilibrium. As the M1
equilibrium value approaches the M1 carrying
capacity in the original model, a Hopf bifurcation (see Appendix 2
)
occurs at  = 0.09
(see Fig. 2
). The periodic orbit associated with this Hopf bifurcation
undergoes a number of period-doubling bifurcations (see Appendix 2
),
which leads to more complicated cycling behavior. An example of the
temporal dynamics when
= 0.09
(see Fig. 2
). The periodic orbit associated with this Hopf bifurcation
undergoes a number of period-doubling bifurcations (see Appendix 2
),
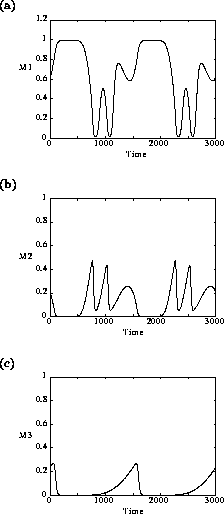
which leads to more complicated cycling behavior. An example of the
temporal dynamics when
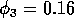 is shown in
Fig. 4
. The
minima of the M2 and
M3 cycles, in particular, get very small (on
the order of 10-15, according to XPPAUT's data
window). From a practical viewpoint, these populations would be
considered extinct due to statistical variation, in which case the
plant population would increase to its carrying capacity for these
values of
is shown in
Fig. 4
. The
minima of the M2 and
M3 cycles, in particular, get very small (on
the order of 10-15, according to XPPAUT's data
window). From a practical viewpoint, these populations would be
considered extinct due to statistical variation, in which case the
plant population would increase to its carrying capacity for these
values of  . This
is exactly the case for the modified model (see Fig. 3
). Thus, the
upper Hopf bifurcation may be an artifact of ratio-dependent
models. This will be discussed in more detail later.
. This
is exactly the case for the modified model (see Fig. 3
). Thus, the
upper Hopf bifurcation may be an artifact of ratio-dependent
models. This will be discussed in more detail later.
FIGURE 2:
One-parameter bifurcation diagrams showing the effects of
varying  on (a)
on (a) 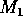 , (b)
, (b) 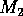 and (c)
and (c) 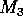 for the original model.
for the original model.
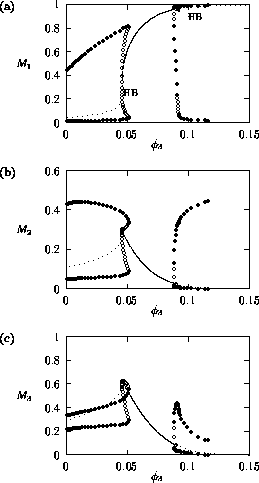
FIGURE 3:
One-parameter bifurcation diagrams showing the effects of
varying  on (a)
on (a) 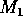 , (b)
, (b) 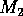 and (c)
and (c) 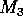 for the modified model.
for the modified model.
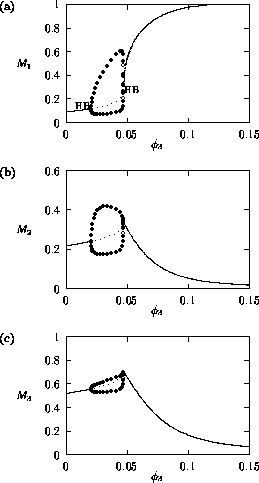
FIGURE 4:
Time plots showing the behavior of (a) 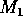 , (b)
, (b) 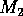 and (c)
and (c) 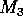 when
when 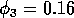 in the original model. Two
complete cycles are shown in the figures.
in the original model. Two
complete cycles are shown in the figures.
These low minima also lead to numerical difficulties, resulting
from the way in which the model is formulated, particularly the
dependence of many of the terms on the ratio
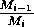 . These ratios become difficult to
evaluate numerically as Mi approaches zero,
causing the ratio to tend to infinity. XPPAUT fails to calculate zero
isoclines, whereas AUTO often enters an infinite loop if such a
situation arises and may crash. Setting a fairly low total number of
steps for a continuation sometimes allows AUTO to break out of the
loop and signal nonconvergence. Manually stopping a continuation when
one of the state variables gets very close to zero also prevents the
package from crashing. This explains why the limit cycles in Fig. 2
are only calculated up to
. These ratios become difficult to
evaluate numerically as Mi approaches zero,
causing the ratio to tend to infinity. XPPAUT fails to calculate zero
isoclines, whereas AUTO often enters an infinite loop if such a
situation arises and may crash. Setting a fairly low total number of
steps for a continuation sometimes allows AUTO to break out of the
loop and signal nonconvergence. Manually stopping a continuation when
one of the state variables gets very close to zero also prevents the
package from crashing. This explains why the limit cycles in Fig. 2
are only calculated up to
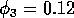 . Such problems do not occur when
using the modified model.
. Such problems do not occur when
using the modified model.
 has a
significant effect on the equilibrium values of the state
variables. This is in agreement with Gutierrez et al. (1994), but the
way in which they arrive at this conclusion is not entirely
correct. Gutierrez et al. (1994) state that a less efficient
parasitoid has a wider C-shaped
M2-isocline. It is true that if
has a
significant effect on the equilibrium values of the state
variables. This is in agreement with Gutierrez et al. (1994), but the
way in which they arrive at this conclusion is not entirely
correct. Gutierrez et al. (1994) state that a less efficient
parasitoid has a wider C-shaped
M2-isocline. It is true that if
 is decreased, the
M2-isocline widens. However, this is
provided that M3 is
constant. If the system is integrated and
M3 is allowed to vary until a new equilibrium
is reached, and the isoclines are plotted with this new equilibrium
M3 value, then the final
M2-isocline may, in fact, have a narrower C
shape than before.
is decreased, the
M2-isocline widens. However, this is
provided that M3 is
constant. If the system is integrated and
M3 is allowed to vary until a new equilibrium
is reached, and the isoclines are plotted with this new equilibrium
M3 value, then the final
M2-isocline may, in fact, have a narrower C
shape than before.
This analysis has shown that the properties of the predator affect the stability of the system as well as the equilibrium magnitudes of the herbivore (directly) and the plant (indirectly). The extent of these effects depends on the properties of both the plant and the herbivore. In the next section, a parameter affecting the herbivore is examined in more detail.
2.2.3 Analysis of a herbivore parameter
Varying  , the
assimilation or conversion efficiency of the herbivore when plants are
abundant, gives the bifurcation diagrams in
Fig. 5
. Comparing Fig. 5
b with Fig. 3
a reveals that they are almost
mirror images. If the mean of the cycle maxima and minima in Fig. 5
a
and Fig. 2
a is taken, then these two figures are also almost mirror
images. That is, decreasing
, the
assimilation or conversion efficiency of the herbivore when plants are
abundant, gives the bifurcation diagrams in
Fig. 5
. Comparing Fig. 5
b with Fig. 3
a reveals that they are almost
mirror images. If the mean of the cycle maxima and minima in Fig. 5
a
and Fig. 2
a is taken, then these two figures are also almost mirror
images. That is, decreasing
 has a very similar effect to
increasing
has a very similar effect to
increasing  . Both
parameters can be thought of as affecting the resistance of the
herbivore to the predator. Decreasing
. Both
parameters can be thought of as affecting the resistance of the
herbivore to the predator. Decreasing
 causes a decline in the condition
of the herbivore, because it cannot convert food as effectively. As a
result, the detrimental effect of the predator on the herbivore is
greater. Increasing
causes a decline in the condition
of the herbivore, because it cannot convert food as effectively. As a
result, the detrimental effect of the predator on the herbivore is
greater. Increasing
 , the availability (nutritional
value) of the herbivore to the predator, achieves the same result but
more directly.
, the availability (nutritional
value) of the herbivore to the predator, achieves the same result but
more directly.
FIGURE 5:
One-parameter bifurcation diagrams showing the effects of
varying  for (a) the original model and (b) the modified
model. The state variable
for (a) the original model and (b) the modified
model. The state variable 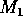 is plotted on the y-axes.
is plotted on the y-axes.
Two-parameter diagrams in
( ,
,
 )-space can be generated by
continuing the Hopf bifurcations in Fig. 5
in two parameters. The
results are shown in
Fig. 6
. These
diagrams show clearly that decreasing
)-space can be generated by
continuing the Hopf bifurcations in Fig. 5
in two parameters. The
results are shown in
Fig. 6
. These
diagrams show clearly that decreasing
 or increasing
or increasing
 has a similar effect, since the
Hopf bifurcation curves occur roughly along the diagonal that has one
end at the origin. Part of this result could have been predicted from
Gutierrez et al. (1994), because they note that it is the ratio
of
has a similar effect, since the
Hopf bifurcation curves occur roughly along the diagonal that has one
end at the origin. Part of this result could have been predicted from
Gutierrez et al. (1994), because they note that it is the ratio
of  and
and
 that determines the
nature of the herbivore isocline. This inverse relationship is thus
expected. However, the one-parameter bifurcation diagrams give us the
additional information that, for certain parameter ranges, limit
cycles are possible.
that determines the
nature of the herbivore isocline. This inverse relationship is thus
expected. However, the one-parameter bifurcation diagrams give us the
additional information that, for certain parameter ranges, limit
cycles are possible.
FIGURE 6:
Two-parameter bifurcation diagrams showing the effects of
varying both  and
and  on the positions of
the Hopf bifurcations in Figure 5. (a) and (b) correspond to the
original and modified models respectively. The meaning of "less
complex cycles" is made clear in Figure 8.
on the positions of
the Hopf bifurcations in Figure 5. (a) and (b) correspond to the
original and modified models respectively. The meaning of "less
complex cycles" is made clear in Figure 8.
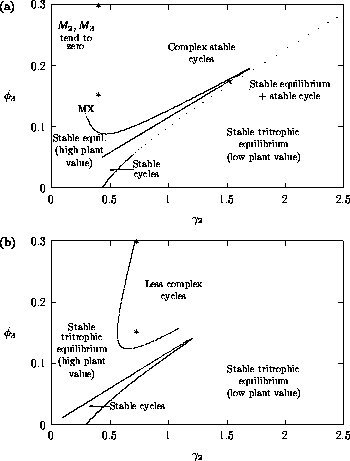
Some important observations can be made by comparing the Fig. 6
diagrams. First, AUTO could not calculate beyond the point denoted by
MX in Fig. 6
a; this problem does not occur in Fig. 6
b. A closer
investigation reveals that the equilibrium values for the state
variables are close to zero in the upper left triangle of the
two-parameter space, and this results in numerical problems when using
the original model. Figure 6
b gives a more complete picture of the
dynamics. There are two regions that correspond to stable cycles,
whereas stable tritrophic equilibria occur in the other region. Low
values of  give
rise to high equilibrium values of M1 and
high values of
give
rise to high equilibrium values of M1 and
high values of  give rise to low equilibrium values, an ecologically important
distinction. A comparison of the two Fig. 6
diagrams shows that the
dynamics for the modified model, although very similar to those for
the original model, are more stable in general. That is, the region
corresponding to tritrophic equilibria is larger and the cycles in the
upper half of the two-parameter space are less complex. These claims
are made clearer in
Fig. 7
and Fig. 8
.
give rise to low equilibrium values, an ecologically important
distinction. A comparison of the two Fig. 6
diagrams shows that the
dynamics for the modified model, although very similar to those for
the original model, are more stable in general. That is, the region
corresponding to tritrophic equilibria is larger and the cycles in the
upper half of the two-parameter space are less complex. These claims
are made clearer in
Fig. 7
and Fig. 8
.
FIGURE 7:
Two-parameter bifurcation diagram of the Hopf bifurcation
continuations in  -space for the modified
model with
-space for the modified
model with  .
.
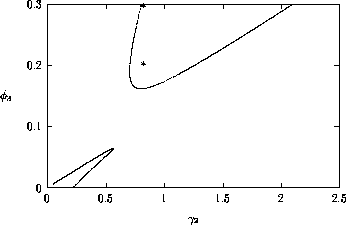
FIGURE 8:
Time plots corresponding to the points marked with *'s in
figures 6(a), 6(b) and 7. (a) These plots were obtained using the
original model with (i) 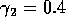 ,
, 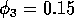 and
(ii)
and
(ii) 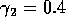 ,
, 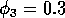 . (b) These plots were
obtained using the modified model with
. (b) These plots were
obtained using the modified model with 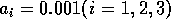 and
and
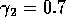 ,
, 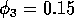 and (ii)
and (ii)
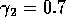 ,
, 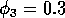 . (c) These plots were obtained
using the modified model with
. (c) These plots were obtained
using the modified model with 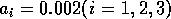 and
(i)
and
(i) 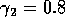 ,
, 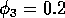 and
(ii)
and
(ii)  ,
,  .
.
Figure 7
shows the
( ,
,
 )-space for the modified model with
ai =0.002 (i = 1,2,3). The
region of stable equilibria is even larger than in Fig. 6
b, resulting
in smaller regions of cycles. The presence of the ai
's seems to have a stabilizing effect on the dynamics of the
system. Figure 8
shows time plots corresponding to points marked with
*'s in the left-hand section of the upper region of cycles in
Figs. 6
a, b, and Fig. 7
. The left-hand portion of this region is where the
values of M2 and M3
are low and, hence, where the nonzero ai 's
have most effect. Clearly, nonzero ai 's
reduce the complexity of the cycles (even for very small values), and
increasing their values also reduces the cycle
amplitude. Additionally, the cycles for the original model
(ai =0, i = 1,2,3) undergo
long periods of extremely low values, which is unrealistic from an
ecological viewpoint.
)-space for the modified model with
ai =0.002 (i = 1,2,3). The
region of stable equilibria is even larger than in Fig. 6
b, resulting
in smaller regions of cycles. The presence of the ai
's seems to have a stabilizing effect on the dynamics of the
system. Figure 8
shows time plots corresponding to points marked with
*'s in the left-hand section of the upper region of cycles in
Figs. 6
a, b, and Fig. 7
. The left-hand portion of this region is where the
values of M2 and M3
are low and, hence, where the nonzero ai 's
have most effect. Clearly, nonzero ai 's
reduce the complexity of the cycles (even for very small values), and
increasing their values also reduces the cycle
amplitude. Additionally, the cycles for the original model
(ai =0, i = 1,2,3) undergo
long periods of extremely low values, which is unrealistic from an
ecological viewpoint.
2.2.4 The role played by the isocline configurations
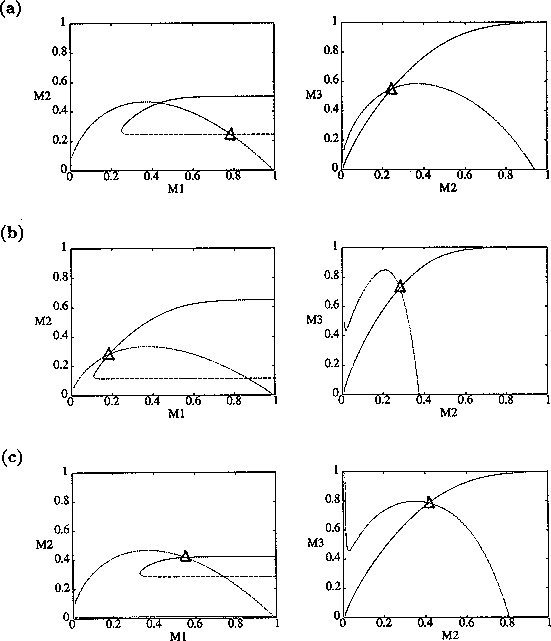
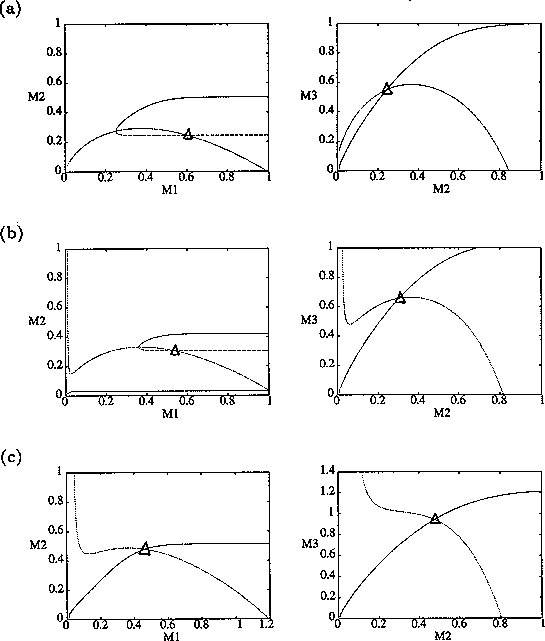
From their isocline analysis, Gutierrez et al. (1994) concluded that the parasitoid Epidinocarsis lopezi could control the cassava mealybug, whereas E. diversicornis could not. However, with three state variables all having similar time scales, these deductions are not as straightforward as they may seem. First, the equilibrium isocline configuration in the M1M2(M2M3) phase plane depends on the value of M3(M1) as well as the parameter values. Thus, noting how an isocline changes as a parameter is varied does not give a complete picture. Second, it is impossible to tell from the qualitative structure of the isoclines which intersection point in the M1M2 plane corresponds to a tritrophic equilibrium. Figure 9 shows three possibilities. Two of these (Fig. 9 b and c) appear in Gutierrez et al. (1994), who assumed, incorrectly, that the equilibrium point in Fig. 9 b was unstable.
FIGURE 9:
Examples of isocline configurations showing the different
possibilities for the position of the tritrophic equilibrium.
Even if the exact position of the equilibrium point is known, it is
impossible to tell, from the qualitative structure of the isoclines,
whether this point is stable or unstable and whether or not limit
cycles occur. For example, although altering the parameter
 has no effect on the
isoclines, low values of
has no effect on the
isoclines, low values of
 give rise to unstable fixed points
and stable limit cycles, and high values give rise to a stable
equilibrium (see Fig. 1
). Thus, numerical computation is needed to
determine the exact location as well as the local stability of an
equilibrium point for the current model.
give rise to unstable fixed points
and stable limit cycles, and high values give rise to a stable
equilibrium (see Fig. 1
). Thus, numerical computation is needed to
determine the exact location as well as the local stability of an
equilibrium point for the current model.
In general, it is the proximity of the tritrophic equilibrium point to the peaks of the M1 and M2 isoclines in the M1M2 and M2M3 planes, respectively, that is important for determining the robustness of model behavior with respect to parameter perturbations. If the equilibrium point is close to one of these peaks, then a small parameter perturbation may change the qualitative structure of the isoclines and, hence, the dynamics. However, to obtain this information, the exact equilibrium isocline configuration for a given set of parameter values needs to be known.
By inference, these criticisms have all noted that if the exact positions of the isoclines and the tritrophic equilibrium were known in both phase planes, then we could obtain a fair amount of information from them. Using XPPAUT, this is possible. In particular, the effects of introducing nonzero values for the ai's can be studied. Figure 10 shows the results obtained using the reference parameter set for model 1 (Eq. A1.1) of Appendix 1 with ai = 0, ai = 0.001, and ai = 0.005 (i = 1, 2, 3).
FIGURE 10:
Isocline configurations for (a) 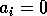 , (b)
, (b) 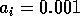 and (c)
and (c) 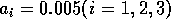 together with the reference parameter
set.
together with the reference parameter
set.
A comparison of Fig. 10
a and b demonstrates that introducing the
ai's prevents the M1
and M2 isoclines from passing through the
origin. Hence, the equilibrium values for the state variables do not
approach zero as rapidly as for the original model, and the modified
model is more robust to parameter variations in this region of low
biomasses. Increasing the ai's from 0.001 to
0.005 reduces the humped shape of the M1 and
M2 isoclines. The result is an even more
robust model. In fact, when ai = 0.005
(i = 1, 2, 3), no regions of cycling behavior are
encountered when the various parameters are altered. Because values of
0.005 are still small, this suggests that the model is structurally
unstable and, hence, predictions from ratio-dependent models should be
treated with caution.
2.3 Discussion The preceding analysis has shown how XPPAUT and AUTO can be used to study the effects of various parameters on the behavior of the ratio-dependent model of Gutierrez et al. (1994). Regions of stable equilibria, sustained oscillations, and multiple equilibria were located in this study. The limitations of an isocline analysis in this three-dimensional setting were also discussed, thus supporting the need for new techniques such as the dynamical systems ones.
The ease with which models may be studied using XPPAUT allowed the simultaneous study of the original model and a modified one. I concluded that the original model is structurally unstable, because a small perturbation to the ratio-dependent terms has a significant effect on the dynamics. This supports the argument that ratio-dependent models exhibit pathological behavior and are not valid near the axes (see the background information for ratio-dependent models in Appendix 1 ). Thus, they cannot be used to study extinction or situations in which one of the state variables attains low values. However, the model by Gutierrez et al. (1994) that has been analyzed is a biological control model whose aim is to suggest what kind of predator can keep herbivore numbers low.
This paper aims to show the usefulness of dynamical systems computer packages and to indicate the ease with which they may be used to gain insights into the behavior of a model and, thus, concentrates on these points. However, the arguments should not be taken out of context. My claim is not that the packages provide a comprehensive way in which to study ecological models. Instead, they should be seen as aids to be used in conjunction with other methods of analysis. Also, these packages do have their limitations. They can only be used to study systems of ordinary differential equations where all the functions are continuous (although simple step functions can often be approximated by continuous functions, as is done in Appendix 4 for the sheep-hyrax-lynx model). Other types of models require different methods of analysis. The packages also require an initial set of parameter values to be chosen. Thus, other techniques are required for theoretical studies that aim to find the exact parameter relationships giving rise to different types of behavior. However, numerical studies can be useful for indicating the relationships that do exist, and thus can provide direction for theoretical studies.
Wollkind et al. (1988) use the latter definition to examine the resilience of their model system for predator-prey mite interactions to changes in food quality of prey for conversion into predator births. This resilience depends on the range of parameter values that give rise to a certain type of qualitative behavior. The wider this range, the greater the systemØs resilience to perturbations of the relevant parameter, provided the parameter is not too near the range endpoints.
Collings and Wollkind (1990) discuss the resilience of various stable phenomena in their model, which exhibits metastability. In this case, the resilience is in terms of the magnitude of population (rather than parameter) perturbations that the system can withstand. If a stable phenomenon has a small domain of attraction (see Appendix 2), then small changes to the populations can lead to dramatic changes in system behavior. Such a system is not resilient.
Both of these studies used bifurcation diagrams to obtain results. Thus, bifurcation diagrams can characterize the resilience of a model system to both parameter and population perturbations. In the sheep-hyrax-lynx model in Appendix 4, the stable equilibrium behavior predominates for wide ranges of the parameter values that were considered. Because there was only a single equilibrium point, the system is resilient to both population perturbations and perturbations in the sheep female culling normal (SFCN), provided SFCN is within the desirable range of values and the initial population values are reasonable.
The ratio-dependent model is less resilient, in that parameter
perturbations can push the system from stable equilibrium behavior
into oscillatory behavior and vice versa. However, Fig. 6
shows that
the regions of stable and oscillatory behavior in
 space are fairly large. Hence, for
parameter combinations that are well within these regions, the system
is resilient to small perturbations in
space are fairly large. Hence, for
parameter combinations that are well within these regions, the system
is resilient to small perturbations in
 and
and
 .
.
The results obtained were compared with those from traditional approaches. AUTO improved on some approximations that Bazykin (1974) made in his analytical study of a predator-prey model. In the sheep-hyrax-lynx model (Swart and Hearne 1989), the bifurcation diagrams gave more information than a traditional sensitivity analysis. This highlighted a relationship that had been omitted from the model. Thus, the dynamical systems techniques can be helpful in constructing better models.
For the ratio-dependent model (Gutierrez et al. 1994), XPPAUT allowed two variations of the model to be studied simultaneously. The resulting conclusion was that the original model is structurally unstable, due to its ratio-dependent terms. The dynamical systems techniques also highlighted the limitations of an isocline analysis in a three-dimensional setting.
In addition, the bifurcation diagrams can be used to characterize the resilience of models to both parameter and population perturbations.
The most important point of this paper is that dynamical systems software was used to arrive at these conclusions. A complete understanding of the underlying mathematical techniques is not required to obtain useful information about the behavior of a model. The software also allows complicated models to be analyzed in greater depth than was previously possible. It is also possible to study discrete models, the topic of a second paper.
None of the models in this paper has a seasonal component. Seasonality plays an important role in the dynamics of many natural systems; thus, studies of models that include such components would be of interest. A few such studies using dynamical systems techniques have been done (e.g., Rinaldi et al. 1993, Gragnani and Rinaldi 1995), but the bifurcation structure is more complicated than that discussed in this paper and requires a continuation package that can handle higher codimension bifurcations, such as LOCBIF (Khibnik et al. 1993; see Appendix 5). Because this paper is intended to introduce the application of dynamical systems techniques to ecological models, I have not included one of these more complex examples.
Responses to this article are invited. If accepted for publication, your response will be hyperlinked to the article. To submit a comment, follow this link. To read comments already accepted, follow this link.
- Abrams, P.A. 1994. The fallacies of
"ratio-dependent'' predation. Ecology 75(6): 1842-1850.
- Akçakaya, H.R., R. Arditi, and L.R. Ginzburg. 1995. Ratio-dependent predation: an abstraction that works. Ecology 76(3): 995-1004.
- Allgower, E.L., and K. Georg. 1992. Continuation and path following. Acta Numerica 1-64.
- Arditi, R., and H. Saïah. 1992. Empirical evidence of the role of heterogeneity in ratio-dependent consumption. Ecology 73(5):1544-1551.
- Arnold, V.I. 1983. Geometrical methods in the theory of ordinary differential equations. Springer-Verlag, New York, New York, USA.
- Aronson, D.G., M.A. Chory, G.R. Hall, and R.P. McGehee. 1982. Bifurcations from an invariant circle for two-parameter families of maps of the plane: a computer-assisted study. Communications in Mathematical Physics 83: 303-354.
- Back, A., J. Guckenheimer, M. Myers, F. Wicklin, and P. Worfolk. 1992. dstool: computer-assisted exploration of dynamical systems. Notices of the American Mathematical Society 39: 303-309.
- Bazykin, A.D. 1974. Volterra's system and the Michaelis-Menten equation. Pages 103-142 in V.A. Ratner, editor. Problems in mathematical genetics. U.S.S.R. Academy of Science, Novosibirsk, U.S.S.R.
- Beddington, J.R., C.A. Free, and J.H. Lawton. 1975. Dynamic complexity in predator-prey models framed in difference equations. Nature 255: 58-60.
- Beddington, J.R., C.A. Free, and J.H. Lawton. 1976. Concepts of stability and resilience in predator-prey models. Journal of Animal Ecology 45: 791-816.
- Berlinski, D. 1976. On systems analysis: an essay concerning the limitations of some mathematical methods in the social, political, and biological sciences. Massachusetts Institute of Technology Press, Cambridge, Massachusetts, USA.
- Berryman, A.A. 1992. The origins and evolution of predator-prey theory. Ecology 73(5): 1530-1535.
- Brylinski, M. 1972. Steady-state sensitivity analysis of energy flow in a marine ecosystem Pages xxx-xxx in B.C. Patten, editor. Systems analysis and simulation in ecology, II. Academic Press, New York, New York, USA.
- Collings, J.B., and D.J. Wollkind. 1990. A global analysis of a temperature-dependent model system for a mite predator-prey interaction. SIAM Journal of Applied Mathematics 50(5): 1348-1372.
- Collings, J.B., D.J. Wollkind, and M.E. Moody. 1990. Outbreaks and oscillations in a temperature-dependent model for a mite predator-prey interaction. Theoretical Population Biology 38: 159-191.
- Deuflhard, P., B. Fiedler, and P. Kunkel. 1987. Efficient numerical pathfollowing beyond critical points. SIAM Journal of Numerical Analysis 24: 912-927.
- Doedel, E.J. 1981. AUTO: a program for the automatic bifurcation analysis of autonomous systems. Congressus Numerantium 30: 265-284.
- Dowden, P.B., H.A. Jaynes, and V.M. Carolin. 1953. The role of birds in a spruce budworm outbreak in Maine. Journal of Economic Entomology 46: 307-312.
- Edelstein-Keshet, L. 1988. Mathematical models in biology. Random House, New York, New York, USA.
- Ermentrout, G.B. 1995. XPPAUT 1.63: the differential equations tool.
- Fairen, V., and M.G. Velarde. 1979. Time-periodic oscillations in a model for respiratory process of a bacterial culture. Journal of Mathematical Biology 8: 147-157.
- Fitzhugh, R. 1961. Impulses and physiological states in theoretical models of nerve membrane. Biophysical Journal 1: 445-466.
- Forrester, J.W.1961. Industrial dynamics. Massachusetts Institute of Technology Press, Cambridge, Massachusetts, USA.
- Frank, P.M. 1978. Introduction to system sensitivity theory. Academic Press, New York, New York, USA.
- Freedman, H.I., and R.M. Mathsen. 1993. Persistence in predator-prey systems with ratio-dependent predator influence. Bulletin of Mathematical Biology 55(4): 817-827.
- Gerald, C.F., and P.O. Wheatley. 1989. Applied numerical analysis. Addison-Wesley, Reading, Massachusetts, USA.
- Gilpin, M.E. 1974. A model of the predator-prey relationship. Theoretical Population Biology 5: 333-344.
- Ginzburg, L.R., and H.R. Akçakaya. 1992. Consequences of ratio-dependent predation for steady-state properties of ecosystems. Ecology 73(5): 1536-1543.
- Gleeson, S.K. 1994. Density dependence is better than ratio dependence. Ecology 75(6): 1834-1835.
- Gragnani, A., and S. Rinaldi. 1995. A universal bifurcation diagram for seasonally perturbed predator-prey models. Bulletin of Mathematical Biology 57(5): 701-712.
- Guckenheimer, J., and P. Holmes. 1983. Nonlinear oscillations, dynamical systems, and bifurcation of vector fields. Springer-Verlag, New York, New York, USA.
- Gutierrez, A.P. 1992. Physiological basis of ratio-dependent predator-prey theory: the metabolic pool model as a paradigm. Ecology 73(5): 1552-1563.
- Gutierrez, A.P., N.J. Mills, S.J. Schreiber, and C.K. Ellis. 1994. A physiologically based tritrophic perspective on bottom up-top down regulation of populations. Ecology 75: 2227-2242.
- Hadamard, J. 1952. Lectures on Cauchy's problem in linear partial differential equations. Dover, New York, New York, USA.
- Hale, J.K., and H. Kogak. 1989. Differential and difference equations through computer experiments. Springer-Verlag, New York, New York, USA.
- Hanski, I. 1991. The functional response of predators: worries about scale. Trends in Ecology and Evolution 6(5): 141-142.
- Hearne, J.W. 1987. An approach to resolving the parameter sensitivity problem in system dynamics methodology. Applied Mathematical Modelling 11: 315-318.
- Hethcote, H.W. 1976. Qualitative analyses of communicable disease models. Mathematical Biosciences 28: 335-356.
- Holling, C.S. 1965. The functional response of predators to prey density and its role in mimicry and population regulation. Memoirs of the Entomological Society of Canada 45: 1-60.
- ______ . 1973. Resilience and stability of ecological systems. Annual Review of Ecology and Systematics 4: 1-23.
- Hultquist, P.F. 1988. Numerical methods for engineers and computer scientists. Benjamin Cummings, Menlo Park, California, USA.
- Jeffers, J.N.R. 1978. An introduction to systems analysis with ecological applications. University Park Press, Baltimore, Maryland, USA.
- Kaas-Petersen, C. 1989. PATH: user's guide. University of Leeds, Leeds, UK.
- Khibnik, A., Y. Kuznetsov, V. Levitin, and E. Nikolaev. 1993. Continuation techniques and interactive software for bifurcation analysis of ordinary differential equations and iterated maps. Physica D 62: 360-371.
- Kowal, N.E. 1971. A rationale for modeling dynamic ecological systems. Pages xxx-xxx in B.C. Patten, editor. Systems analysis and simulation in ecology, I. Academic Press, New York, New York, USA.
- Ludwig, D., D.D. Jones, and C.S. Holling. 1978. Qualitative analysis of insect outbreak systems: the spruce budworm and forest. Journal of Animal Ecology 47: 315-332.
- Lundberg, P., and J.M. Fryxell. 1995. Expected population density vs. productivity in ratio-dependent and prey-dependent models. American Naturalist 146(1): 153-161.
- MacDonald, N. 1978. Time lags in biological models. Springer-Verlag, Berlin, Germany.
- ______ . 1989. Biological delay systems. Cambridge University Press, Cambridge, Massachusetts, USA.
- May, R.M. 1973. Time delay vs. stability in population models with two and three trophic levels. Ecology 54: 315-325.
- ______ . 1981. Models for two interacting populations. Pages 78-104 in R.M. May, editor. Theoretical ecology: principles and applications. Blackwell, Oxford, UK.
- Maynard Smith, J. 1974. Models in ecology. Cambridge University Press, Cambridge, UK.
- McCarthy, M.A., L.R. Ginzburg, and H.R. Akçakaya. 1995. Predator interference across trophic chains. Ecology 76(4): 1310-1319.
- Murray, J.D. 1981. A pre-pattern formation mechanism for animal coat markings. Journal of Theoretical Biology 88: 161-199.
- Nusse, H.E., and J.A. Yorke. 1994. Dynamics: numerical explorations. Applied Mathematical Sciences 101. Springer-Verlag, New York, New York, USA.
- Patten, B.C. 1971. A primer for ecological modeling and simulation with analog and digital computers. Pages xxx-xxx in B.C. Patten, editor. Systems analysis and simulation in ecology, I. Academic Press, New York, New York, USA.
- Rheinboldt, W.C., and J.V. Burkardt. 1983a . A locally parameterized continuation process. ACM Transactions on Mathematical Software 9: 215-235.
- Rheinboldt, W.C., and J.V. Burkardt. 1983b. Algorithm 596: a program for a locally parametrized continuation process. ACM Transactions on Mathematical Software 9: 236-241.
- Rinaldi, S., S. Muratori, and Y. Kuznetsov. 1993. Multiple attractors, catastrophes, and chaos in seasonally perturbed predator-prey communities. Bulletin of Mathematical Biology 55(1): 15-35.
- Rosenzweig, M.L., and R.H. MacArthur. 1963. Graphic representation and stability conditions of predator-prey interactions. American Naturalist 97: 209-223.
- Royama, T. 1984. Population dynamics of the spruce budworm Choristoneura fumiferana. Ecological Monographs 54(4): 429-462.
- Sanders, C.J., R.W. Stark, E.J. Mullins, and J. Murphy, editors. 1985. Recent advances in spruce budworm research. Proceedings of CANUSA Spruce Budworm Research Symposium, 16-20 September 1984, Bangor, Maine, Canadian Forestry Service, Ottawa, Ontario, Canada.
- Sarnelle, O. 1994. Inferring process from pattern: trophic-level abundances and imbedded interactions. Ecology 75(6): 1835-1841.
- Seydel, R. 1988. From equilibrium to chaos: practical bifurcation and stability analysis. Elsevier, New York, New York, USA.
- ______ . 1991. BIFPACK: a program package for continuation, bifurcation, and stability analysis. Version 2.3+. University of Ulm, Ulm, Germany.
- Strogatz, S.H. 1994. Nonlinear dynamics and chaos. Addison-Wesley, Reading, Massachusetts, USA.
- Swart, J. 1987. Sensitivity of a hyrax-lynx mathematical model to parameter uncertainty. South African Journal of Science 83: 545-547.
- Swart, J., and J.W. Hearne. 1989. A mathematical model to analyze predation and competition problems in a sheep-farming region. System Dynamics Review 5: 35-50.
- Tomovic, R. 1963. Sensitivity analysis of dynamic systems. Translated by D. Tornquist. McGraw-Hill, London, UK.
- Waterloo Maple Software. 1990-1992. The maple roots report. Waterloo Maple Software, Waterloo, Canada.
- Watt, K.E.F. 1966. The nature of systems analysis. Pages xxx-xxx in K.E.F. Watt, editor. Systems analysis in ecology. Academic Press, New York, New York, USA.
- Wiggins, S. 1990. Introduction to applied nonlinear dynamical systems and chaos. Springer-Verlag, New York, New York, USA.
- Williams, T., and C. Kelley. 1986. GNUPLOT: an interactive plotting program: user manual. http://www.cs.dartmouth.edu/gnuplot/gnuplot.html
- Wollkind, D.J., J.B. Collings, and J.A. Logan. 1988. Metastability in a temperature-dependent model system for predator-prey mite outbreak interactions on fruit trees. Bulletin of Mathematical Biology 50(4): 379-409.
- Yodzis, P. 1989. Introduction to theoretical ecology. Harper and Row, New York, New York, USA.
- Akçakaya, H.R., R. Arditi, and L.R. Ginzburg. 1995. Ratio-dependent predation: an abstraction that works. Ecology 76(3): 995-1004.
DETAILS FOR THE RATIO-DEPENDENT MODEL
A1.1 Background Ratio-dependent models assume that the functional response terms depend on ratios of the state variables rather than on absolute values or products of variables, as is the case for classical models. Although not a new idea, the concept of ratio dependence in predator-prey interactions has been approached with fresh interest in ecological theory in recent years (Berryman 1992).
One advantages of such models is that they prevent the paradoxes of enrichment and biological control predicted by classical models (Berryman 1992). Experimental observations of Arditi and Saïah (1992) suggest that prey-dependent models are appropriate in homogeneous situations and ratio-dependent models are appropriate in heterogeneous situations. Based on their work, Ginzburg and Akçakaya (1992) and McCarthy et al. (1995) also conclude that natural systems are closer to ratio dependence than to prey-dependence. Gutierrez (1992) develops a physiological basis for the theory.
Gleeson (1994), however, questions the assumptions of ratio-dependent models, noting that direct density dependence, or self-regulation, in the top consumer is sufficient to preclude the paradox of enrichment from classical models. From his work on whether patterns among trophic levels are a reliable way to distinguish between prey- and ratio dependence, Sarnelle (1994) concludes that the ratio-dependent approach should be applied only when predator and prey are the top two trophic levels in an ecosystem. Abrams (1994) argues that patterns and experimental results used in support of ratio-dependent predation are consistent with numerous other explanations, and that these other explanations do not suffer from pathological behaviors and a lack of plausible mechanism, as do ratio-dependent models. Lundberg and Fryxell (1995) note the difficulty of distinguishing between competing hypotheses without a proper mechanistic understanding of the processes involved.
In a recent paper, Akçakaya et al. (1995) respond to some of these criticisms. The argument relevant to my present paper concerns their refutation of the pathological behavior of ratio-dependent models. Freedman and Mathsen (1993) note that ratio-dependent models are invalid near the axes (that is, where the state variables are close to zero), because the ratios tend to infinity in these regions. As a result, even when prey (resource) densities are very low, ratio-dependent models predict a positive rate of predator (consumer) increase, provided that predator densities are low enough, because the number of prey available per predator increases to infinity as predator density declines to zero (Abrams 1994, Gleeson 1994). In terms of isoclines, the problem stems from the fact that the predator isocline passes through the origin in ratio-dependent models, which means that, even at low prey densities, a sufficiently small predator population can increase. According to Hanski (1991), this is against intuition and many field observations. It also means that ratio-dependent models cannot be used to study the extinction of species.
However, Akçakaya et al. (1995) state that these problems near the axes are only pathological in a mathematical sense; in biological terms, both species would increase initially, and then predators would consume all the prey and both species would become extinct. Because prey-dependent models cannot predict this outcome, they are pathological in a biological sense. In the next section, however, I will show that ratio-dependent models do not necessarily predict this outcome either. I will describe a ratio-dependent model that predicts oscillations of large amplitude in these "pathological" regions (see Fig. 2 ). Although these large-amplitude oscillations may be interpreted as signaling extinction from a practical viewpoint, this is not the prediction of the ratio-dependent model.
Akçakaya et al. (1995) state that:
A realistic model of prey-predator interactions should be able to predict the whole range of dynamics observed in such systems in nature. A ratio-dependent model can have stable equilibria, limit cycles, and the extinction of both species as a result of over exploitation.However, a few sentences later, they agree that ratio-dependent models are not valid at very low densities (a precursor of extinction); earlier in the paper, they state that " it is at the extremes of low and high densities that strict ratio dependence may not be valid."
In an attempt to clarify some of the arguments in this debate, I introduce a small modification to the ratio-dependent model of Gutierrez et al. (1994) and study this modified model in conjunction with the original one. The analysis to follow shows that the original model is structurally unstable, because a small perturbation to the ratio-dependent terms substantially alters the dynamics.
A1.2 Model equations
The model equations are functionally homogeneous (i.e., all three equations contain the same basic terms), because the authors argue that the same generalized functional and numerical responses must describe the search, acquisition, and conversion of all organisms as they seek to satisfy their metabolic requirements. Details of the model formulation can be found in Gutierrez et al. (1994). The final equations are:
where M1 is the biomass of plants, M2 is the biomass of herbivores, and M3 is the biomass of predators. The parameters
 represent assimilation rates corrected for the efficiency of biomass conversion;
represent assimilation rates corrected for the efficiency of biomass conversion;
 represents the proportion of the resource that is available to its consumers (that is, its apparency); Di is the per unit demand of the consumer for resources; ri is the base respiration rate corrected for the efficiency of biomass conversion; and bi is the degree of self-limitation. M0 represents a biomass equivalent of the light energy incident in the growing space of the plants, and
represents the proportion of the resource that is available to its consumers (that is, its apparency); Di is the per unit demand of the consumer for resources; ri is the base respiration rate corrected for the efficiency of biomass conversion; and bi is the degree of self-limitation. M0 represents a biomass equivalent of the light energy incident in the growing space of the plants, and
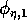 and
and
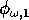 (which both lie between 0 and 1) scale the potential photosynthesis rate to the realized rate.
(which both lie between 0 and 1) scale the potential photosynthesis rate to the realized rate.
The respiration term, riMi1 + bi, requires further explanation. Respiration usually increases with population density (Gutierrez et al. 1994) and, thus, should be an increasing function of Mi. However, introducing such a functional dependence increases the model's complexity. Because the effect is usually small, the authors chose the simpler formulation riMi1 + bi, where bi has a value between 0.02 and 0.05. The disadvantage of this choice is that ri must have rather unusual units (grams per bi per day, where grams are the units of Mi) that depend on bi. Thus, the term riMi1 + bi has the same units as
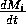 (namely, grams per day, where grams are the units of Mi). This dependence of the units on bi is not satisfactory from a mathematical viewpoint, but since bi is small, I chose to ignore this initially. In the next section, I discuss a small alteration to the model that takes care of the difficulty.
(namely, grams per day, where grams are the units of Mi). This dependence of the units on bi is not satisfactory from a mathematical viewpoint, but since bi is small, I chose to ignore this initially. In the next section, I discuss a small alteration to the model that takes care of the difficulty.
Gutierrez et al. (1994) use parameter values corresponding to a cassava (Manihotesculenta Crantz)-mealybug (Phenacoccuss manihoti Mat.-Ferr.)-parasitoid system in Africa. They claim that their analysis demonstrates that the parasitoid Epidinocarsis lopezi (De Santis) can control the mealybug (except on poor soils), whereas E. diversicornis (Howard) and native natural enemies cannot. However, the parameter values for the cassava-mealybug-parasitoid system given to me by the authors (only values for
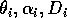 are reported in the paper) did not yield the isocline configurations or the behavior that they described. I then scaled the equations to get a better idea of the relative magnitudes of the parameters. The procedure involved is discussed in the next section.
are reported in the paper) did not yield the isocline configurations or the behavior that they described. I then scaled the equations to get a better idea of the relative magnitudes of the parameters. The procedure involved is discussed in the next section.
A1.3 Nondimensionalization
The technique of nondimensionalizing, or scaling, is commonly used to simplify a system of equations because it has many other advantages. It illuminates which parameters are most important in determining the dynamics of the model (Edelstein-Keshet 1988) and gives insight into the relative magnitudes of the parameters required to produce biologically reasonable behavior. Also, the state variables are scaled so that they all have the same order of magnitude, say between 0 and 1. This is important when solving the equations numerically, as very different magnitudes can lead to computer round-off errors (Gerald and Wheatley 1989). In the cassava-mealybug-parasitoid system, the biomass of cassava is much larger than that of the mealybug and the parasitoid (cassava mass averages ~ 2 kg, whereas the mealybug and parasitoids have average masses of ~ 2 mg). Scaling, at least, is thus vital. (For an introduction to nondimensionalizing systems of ordinary differential equations, see Edelstein-Keshet 1988.)
Natural scalings for the state variables are given by their carrying capacities when resources are abundant. Gutierrez et al. (1994) calculate these to be
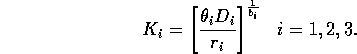
Replacing
Mi
by
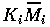 (i=1,2,3) , and t by
(i=1,2,3) , and t by
 (here Ki has the dimensions of Mi and
(here Ki has the dimensions of Mi and
 the dimensions of t; hence,
the dimensions of t; hence,
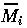 (i =1,2,3) and t* are dimensionless variables) and choosing the dimensionless combinations of parameters
(i =1,2,3) and t* are dimensionless variables) and choosing the dimensionless combinations of parameters
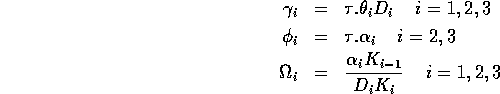 ,
,
where K0 = M0 gives the nondimensionalized Eqs. A1.2, where I have replaced
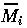 by Mi and t* by t for convenience:
by Mi and t* by t for convenience:
(I replaced the product
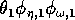 by
by
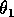 , because all three parameters have the same effect on the dynamics and, thus, do not need to be considered separately.)
, because all three parameters have the same effect on the dynamics and, thus, do not need to be considered separately.)
The choice of dimensionless parameters is not unique. Other combinations would have led to slightly different final equations, but the choices here lend themselves to biological interpretation. For example,
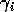 can be thought of as the potential per unit biomass growth rate (Gutierrez et al. 1994), or as the conversion efficiency of the consumer in converting the resource into biomass.
can be thought of as the potential per unit biomass growth rate (Gutierrez et al. 1994), or as the conversion efficiency of the consumer in converting the resource into biomass.
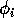 can be thought of as the availability of the resource to the consumer, or perhaps the nutritional value of the resource.
can be thought of as the availability of the resource to the consumer, or perhaps the nutritional value of the resource.
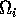 is made up of a ratio of quantities. The numerator can be thought of as the maximum amount of resource available to the consumer, and the denominator as the maximum demand of consumers for resource. More simply,
is made up of a ratio of quantities. The numerator can be thought of as the maximum amount of resource available to the consumer, and the denominator as the maximum demand of consumers for resource. More simply,
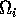 gives a measure of the ratio of supply to demand. Results in Gutierrez et al. (1994) are based on the relationship between
gives a measure of the ratio of supply to demand. Results in Gutierrez et al. (1994) are based on the relationship between
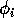 and
and
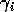 , since
, since
 is just a scaling factor. Hence, results using Eqs. A1.2 are comparable with those in Gutierrez et al. (1994).
is just a scaling factor. Hence, results using Eqs. A1.2 are comparable with those in Gutierrez et al. (1994).
I mentioned earlier that the parameters ri in the original model have units that depend on bi. This can be prevented by replacing the terms riMi1 + bi with terms of the form
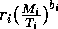 , where Ti has the same units as Mi. Ti can be thought of as a threshold value above which self-limitation becomes noticeable. With this modification, the units of ri are per day, and ri can be interpreted as a respiration rate, as was originally intended. The new carrying capacities are given by
, where Ti has the same units as Mi. Ti can be thought of as a threshold value above which self-limitation becomes noticeable. With this modification, the units of ri are per day, and ri can be interpreted as a respiration rate, as was originally intended. The new carrying capacities are given by
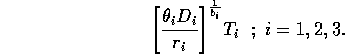
It can be shown that setting the Ki 's equal to these new values and scaling the equations as above results in system (A1.2) once again. Thus, the problems with the respiration term can be ignored in the remainder of the paper.
Having scaled the equations, I needed to choose values for the parameters. An advantage of scaling is that there are now 11 parameters instead of the original 18. For comparison with the results of Gutierrez et al. (1994), I wanted to find values that resulted in isocline configurations similar to those in their paper. XPPAUT calculates and displays isoclines in two dimensions, and parameter values can be altered interactively. Since the competition effect is very small, but difficult to quantify, I followed A. Gutierrez (personal communication) and chose Bi = 0.02 (i = 1,2,3). Values of
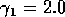 ,
,
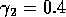 ,
,
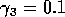 ,
,
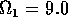 ,
,
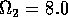 ,
,
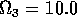 ,
,
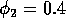 ,
,
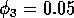 gave the isocline configurations shown in
Fig. 11
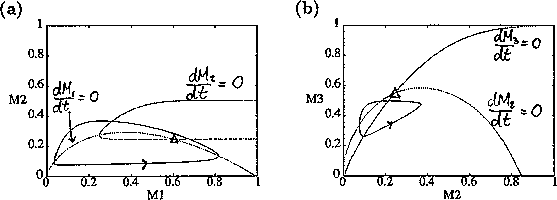
. These isoclines have similar shapes to those in Gutierrez et al. (1994). A noticeable difference is that the M3 -isocline intersects the M2 -isocline to the left of the M2 -peak. In fact, using the techniques in Gutierrez et al. (1994), it would have been impossible to conclude that the tritrophic equilibrium is stable for the isocline configuration shown in Fig. 11, because of the position of the intersection point in the plane. For this parameter set (which I shall call the reference set), there is also a stable limit cycle. The initial values of M1,M2 and M3 determine whether the system approaches the stable equilibrium or the limit cycle.
gave the isocline configurations shown in
Fig. 11
. These isoclines have similar shapes to those in Gutierrez et al. (1994). A noticeable difference is that the M3 -isocline intersects the M2 -isocline to the left of the M2 -peak. In fact, using the techniques in Gutierrez et al. (1994), it would have been impossible to conclude that the tritrophic equilibrium is stable for the isocline configuration shown in Fig. 11, because of the position of the intersection point in the plane. For this parameter set (which I shall call the reference set), there is also a stable limit cycle. The initial values of M1,M2 and M3 determine whether the system approaches the stable equilibrium or the limit cycle.
Biological considerations suggest that these values for the
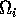 are rather high and that the value for
are rather high and that the value for
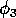 is rather low. However, in the absence of better information and since this parameter set has a nontrivial, stable equilibrium point, it is a convenient starting point.
is rather low. However, in the absence of better information and since this parameter set has a nontrivial, stable equilibrium point, it is a convenient starting point.
Before beginning an analysis of the model, I will introduce a small modification to the equations. Because the problems associated with ratio-dependent models described in section A1.1 involve low population densities, it would be interesting to know what effects a small modification to the model, which prevents the denominators of the ratios from getting too close to zero, would have on the dynamics. Abrams (1994) states that modifications to ratio-dependent models cannot be made biologically realistic because the original models have no clear mechanistic derivation. However, some form of modification that prevents the ratios from tending to infinity may be useful for revealing any spurious behavior near the axes that may result from the ratio dependence.
The ratios in model (A1.2) have the form
 .
.
The difficulties are experienced when Mi approaches zero. Adding a constant in the denominator, that is, replacing the ratio by
would alleviate the problem. Although this addition may appear difficult to justify biologically, Gutierrez (1992) used an exponent of this form in his functional response term. That model is physiologically based, as is the present one.
In model A.1.2 ], the ratio-dependent terms have the form
where k is a parameter or combination of parameters. When the exponent is small, we have
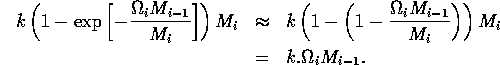 .
.
In order to preserve this property when using the modified term (Eq. A1.3 ), I replaced Eq. A1.4 by
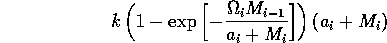 ,
,
where ai is a small constant, say 0.001. The resulting equations are:
If ai = 0 (i = 1, 2, 3) , then the above model is equivalent to system (A1.2).
DYNAMICAL SYSTEMS BASICS
A2.1 Glossary of dynamical systems terminology This appendix lists alphabetically those topics that are required in the main body of the paper and in the appendices. Brief descriptions are given and diagrams are used to explain the concepts as simply and intuitively as possible. A more comprehensive introduction to dynamical systems theory can be found in most introductory dynamical systems texts (e.g., Guckenheimer and Holmes 1983, Seydel 1988). Yodzis (1989) explains the theory using ecological examples, and Strogatz (1994) gives an informal introduction to nonlinear dynamics, with an emphasis on geometric intuition and scientific applications.
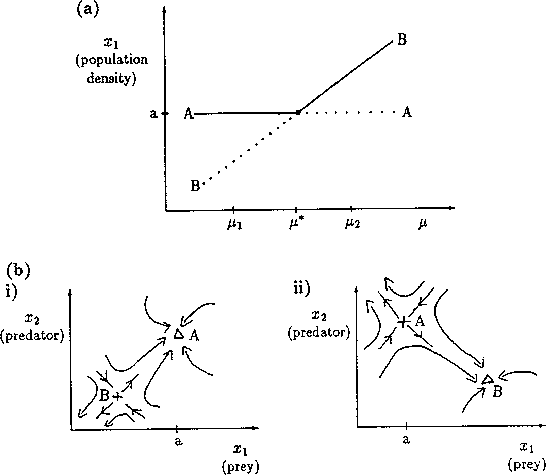
A2.1.1 Bifurcation diagram A one-parameter bifurcation diagram summarizes the qualitative behavior corresponding to different values of a parameter. A state variable, or some function of the state variables, is usually plotted on the y -axis and the parameter on the x -axis. The positions and local stabilities of equilibrium points, as well as periodic orbits, are indicated using different line types. Solid curves are used to represent locally stable equilibria and dotted curves are used for locally unstable equilibria. Maxima and minima of periodic orbits are indicated using circles: solid for stable orbits and open for unstable orbits.
It is important to note that bifurcation diagrams summarize the behavior associated with a range of parameter values. They do not represent the dynamics corresponding to a continually varying parameter (Wiggins 1990). To read a bifurcation diagram, fix the parameter at a particular value and mentally draw a vertical line at that value. Each crossing of this line with a curve in the diagram corresponds to an equilibrium point or a periodic orbit (limit cycle). The local stability properties of a particular phenomenon are given by the type of curve: solid, dotted, or open or closed circles. For example, the phase portraits in Fig. 14b (i) and (ii) were obtained by mentally drawing vertical lines at the parameter values µ = µ1 and µ = µ2, respectively, in Fig. 14a.
FIGURE 14:
(a) A bifurcation diagram of a transcritical bifurcation,
(b)(i) a phase portrait corresponding to 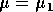 and (b)(ii)
a phase portrait corresponding to
and (b)(ii)
a phase portrait corresponding to  . The stabilities
of the two equilibrium points interchange for parameter values on either
side of the bifurcation point.
. The stabilities
of the two equilibrium points interchange for parameter values on either
side of the bifurcation point.
A two-parameter bifurcation diagram shows how the positions of bifurcation points change as two parameters are varied. For example, if a bifurcation point is encountered in a one-parameter bifurcation diagram, a second parameter may be varied to see how it affects the position of the bifurcation point. An example is shown in Fig. 19.
FIGURE 19:
Two-parameter bifurcation diagram of  -parameter
space for
-parameter
space for  ,
, 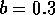 ,
, 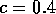 and
and 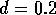 . The regions (i), (ii)
and (iii) correspond to those in Figure 16.
. The regions (i), (ii)
and (iii) correspond to those in Figure 16.
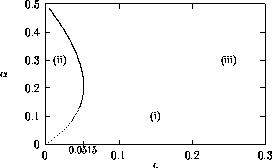
FIGURE 16:
Bazykin's two-parameter bifurcation diagram of
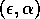 -parameter space.
-parameter space.

A2.1.2 Bifurcation point A bifurcation point is a point in parameter space at which the qualitative behavior of the system changes. A stable equilibrium may become unstable at this point, or there may be a change from a stable equilibrium to oscillatory behavior. Examples can be found in sections A2.1.6, A2.1.8, A2.1.11, and A2.1.19.
A2.1.3 Continuation branch A solution branch, or continuation branch, is a curve of equilibrium points (or limit cycles or bifurcation points) that indicates how the position and properties of the equilibrium point (or limit cycle or bifurcation point) change as a parameter (or parameters) is altered. Together, a number of these branches make up a bifurcation diagram.
A2.1.4 Domain of attraction Suppose the system in which we are interested has a stable equilibrium point (see section A2.1.9). Then the collection of all initial state variable values from which the system tends toward this equilibrium, as time progresses, is the domain (or basin) of attraction of the equilibrium point. The equilibrium point is called an "attractor." Any stable phenomenon, such as a stable limit cycle, also has a domain of attraction and is referred to as an attractor.
A2.1.5 Hard loss of stability In the case of a Hopf bifurcation, this occurs when there is a rapid change from stable equilibrium behavior to stable limit cycles of large amplitude. This results from a subcritical Hopf bifurcation in which the unstable orbit reaches a limit point and turns around to stabilize. An example is shown in Fig. 12. When the parameter µ is increased beyond the Hopf bifurcation at µ*, the system rapidly changes to limit cycles of large amplitude instead of starting off with small limit cycles that grow in size as µ increases, as shown in Fig.15 . Also, as µ is decreased,there is a jump from large-amplitude cycles to a zero-amplitude equilibrium point, but this takes place at µ1, which is less than µ*. For µ1 < µ < µ*, there are two stable attractors, an equilibrium point and a limit cycle. Examples of hard loss of stability arise in the analysis of the ratio-dependent model.
A2.1.6 Hopf bifurcation A Hopf bifurcation (also known as a Poincaré-Andronov-Hopf bifurcation; Arnold 1983, Wiggins 1990) is a bifurcation point at which an equilibrium point alters stability and a limit cycle (period orbit) is initiated. The example in Fig. 15 has a stable limit cycle surrounding an unstable equilibrium point. It is also possible to have an unstable limit cycle encircling a locally stable equilibrium point. Unstable periodic orbits are indicated by open rather than solid circles.
A2.1.7 Limit cycle (See periodic orbit, section A2.12)
A2.1.8 Limit point A limit point or saddle-node bifurcation occurs when there are two equilibrium points on one side of the bifurcation point, but none on the other side. Figure 13a shows an example of a bifurcation diagram of a limit point (LP). For µ < µ*, there are no equilibrium points at which both populations are nonzero. µ* is thus the limiting value of µ for which equilibrium points exist; hence, the name limit point. A possible phase portrait in two dimensions for µ > µ* is shown in Fig. 13b for the particular value µ = µ1. A is a locally stable equilibrium point and B is a saddle point. The initial values of x1 and x2 determine the subsequent behavior of the system. If the initial point is in the domain of attraction of A (to the right of point B in Fig. 13b), then the system will approach A. However, if the initial point lies on the other side of B, it will be repelled away from B in the opposite direction to A. Notice how the size of the domain of attraction of A, in terms of the state variable x1, decreases as µ decreases towards µ* (see Fig. 13a).
A2.1.9 Local stability Suppose the system in which we are interested is disturbed slightly from its equilibrium point. For example, a week of warmer weather may cause an insect's growth rate to increase slightly. If, after the disturbance is removed, the system returns to its original equilibrium, then the equilibrium point is said to be locally stable and is called an "attractor." Otherwise, it is said to be unstable and is a "repeller." Locally stable equilibrium points are called sinks and locally unstable ones are called saddle points or sources.
A2.1.10 Parameter A parameter is a quantity, e.g., fecundity rate or predation rate, that is used in describing the dynamics of a state variable. Although a state variable evolves with time, a parameter is kept constant as time progresses. In this paper, parameter values are varied across ranges of values to see how they affect the qualitative behavior of the state variables. For example, increasing the fecundity rate of a population that is at equilibrium may cause the population to start oscillating.
A2.1.11 Period-doubling bifurcation A period-doubling bifurcation occurs when a limit cycle or periodic orbit undergoes a bifurcation and there is an exchange of stability to orbits having double the period. See Seydel (1988) for a detailed explanation.
A2.1.12 Periodic orbit The terminology periodic orbit is used to describe a state variable (e.g., population density) that is oscillating in a regular, repetitive manner. For continuous models having dimension of at least two, such an orbit is also called a limit cycle, provided that the orbit is isolated (that is, trajectories starting at points near the orbit spiral either toward or away from the cycle; Strogatz 1994).
A2.1.13 Phase portrait Suppose our system is continuous and has two state variables, say a prey (x1) and a predator (x2). We can represent the behavior over time of both populations in a single diagram called a phase portrait. Examples are shown in Figs. 13b and 14b . An illustration of the relationship between time plots and phase portraits can be found in Holling (1973: 3).
A2.1.14 Saddle point A saddle point is an equilibrium point that attracts in certain directions and repels in others. Such an equilibrium point has unstable and stable manifolds. Initial points lying on these manifolds are repelled from, or attracted toward, the equilibrium point, respectively. Other initial points first may be attracted and then repelled (see Edelstein-Keshet 1988).
A2.1.15 Sink A sink is a locally stable equilibrium point and may be either a stable node or a spiral attractor. In the case of a spiral attractor, the state variables oscillate with decreasing amplitude as they approach the equilibrium point.
A2.1.16 Soft loss of stability This occurs at a Hopf bifurcation when there is a continuous change from stable equilibrium behavior to limit cycles of small amplitude. The amplitude of these cycles increases gradually for parameter values further from the Hopf bifurcation. Figure 15 gives an example of soft loss of stability. See also section A2.1.5.
A2.1.17 Source A source is an equilibrium point that is locally unstable. Any disturbance to the system will cause the state variables to move away from this point. In the case of a spiral repeller, this repulsion may be oscillatory.
A2.1.18 State variable Suppose we are interested in a system consisting of plants, herbivores, and predators. Then the"state" of the system can be described by the relative biomasses or densities of these populations. The variables that are used in a mathematical model of the system to represent these biomasses or densities are called state variables.
A2.1.19 Transcritical bifurcation At a transcritical bifurcation point, two equilibrium points coincide and exchange stabilities. An example is shown in Fig. 14. There are two equilibrium points, A and B, at each value of the parameter µ. A is stable for µ < µ* and a saddle point for µ > µ*. The situation is reversed for B. Figures 14b(i) and (ii) show possible phase portraits in two dimensions for µ = µ1 and µ = µ2. Note that the bifurcation diagram in Fig. 14a only indicates the positions of the equilibrium points in terms of one of the state variables, x1.
A2.2 Introduction to dynamical systems concepts In this paper, I am more interested in obtaining qualitative than quantitative information about model behavior. That is, I am more interested in finding out how varying a parameter value affects the modes of behavior of a model, rather than finding the exact parameter values at which these changes occur. Berlinski (1976) notes that qualitative insights are at a much greater depth than partially quantitative results. Because of the uncertainty associated with parameter values in nature (Hadamard 1952, Frank 1978, Swart 1987), and because models are necessarily simplifications of reality, the exact quantitative predictions of a model have little significance. It is the type or mode of behavior that is most important.
Qualitative analyses are concerned mainly with long-term rather than transient behavior. Transient dynamics vary with the initial values of variables and the time period over which solutions are calculated, whereas qualitative studies deal with the eventual behavior of the system once the initial transients have died away.
There are many different modes of behavior that characterize the long-term dynamics of a model. Suppose that the modelØs state variables represent interacting populations. In the long term, any given population may become extinct, reach a stable equilibrium, or oscillate in time. Another mathematical possibility is that a population may grow indefinitely, although this is not biologically plausible except for short time periods. As one or more parameters are varied, it is possible to change from one mode of behavior to another.
Consider the following two-dimensional model due to Bazykin (1974):
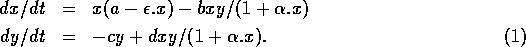
Here, x represents prey density and y predator density. The term ax describes the exponential growth of the prey population in the absence of predators, and
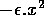 takes into account intraspecific competition among prey. In the absence of the predator, the prey population experiences logistic growth. The term - cy describes the exponential decline in the predator population in the absence of prey. The Holling type-II functions (Holling 1965)
takes into account intraspecific competition among prey. In the absence of the predator, the prey population experiences logistic growth. The term - cy describes the exponential decline in the predator population in the absence of prey. The Holling type-II functions (Holling 1965)
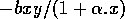 and
and
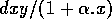 describe the interaction between the two populations.
describe the interaction between the two populations.
If intraspecific competition in the prey population is sufficiently intense (i.e.,
 is sufficiently large), then the prey population reaches a stable equilibrium. However, the equilibrium value is too low to support the predator population and this forces the predator into extinction.
is sufficiently large), then the prey population reaches a stable equilibrium. However, the equilibrium value is too low to support the predator population and this forces the predator into extinction.
If
 is decreased, thus reducing competition among prey, then the predator-prey interaction becomes relatively more important and both populations reach stable equilibria.
is decreased, thus reducing competition among prey, then the predator-prey interaction becomes relatively more important and both populations reach stable equilibria.
If
 is decreased further, the dynamics become more complicated. Instead of reaching a stable equilibrium, the two populations oscillate in time in a sustained manner. This is known as stable limit cycle behavior. For any positive initial values, the predator and prey populations oscillate, with the amplitudes of the oscillations increasing or decreasing until the regular oscillatory pattern corresponding to the limit cycle is reached.
is decreased further, the dynamics become more complicated. Instead of reaching a stable equilibrium, the two populations oscillate in time in a sustained manner. This is known as stable limit cycle behavior. For any positive initial values, the predator and prey populations oscillate, with the amplitudes of the oscillations increasing or decreasing until the regular oscillatory pattern corresponding to the limit cycle is reached.
The exact values of
 at which the previously mentioned changes in qualitative behavior occur are known as bifurcation points. In particular, the transition between equilibrium behavior and limit cycle behavior is known as a Hopf bifurcation (at least in this case; limit cycles can also be generated in other ways).
at which the previously mentioned changes in qualitative behavior occur are known as bifurcation points. In particular, the transition between equilibrium behavior and limit cycle behavior is known as a Hopf bifurcation (at least in this case; limit cycles can also be generated in other ways).
Figure 15 is an example of a one-parameter bifurcation diagram. These diagrams summarize the phase portraits corresponding to different (fixed) values of a parameter, showing how the qualitative behavior of a system of equations changes as a parameter is varied across a range of values. The parameter in question is plotted on the x -axis and one of the state variables (in this case, x) is plotted on the y -axis. Solid lines represent stable equilibria, dotted lines represent unstable equilibria, and solid circles indicate the maxima and minima of stable limit cycles. In order to interpret a bifurcation diagram, imagine the phase portraits corresponding to different values of the parameter. This is done by choosing a particular value of the parameter and mentally drawing a vertical line at that value. The points at which this line crosses the curves in the bifurcation diagram will indicate the points (in terms of the quantity on the y -axis) at which equilibria or limit cycles occur, as well as the stability of these phenomena. This information can be used to construct a possible phase portrait.
From Fig. 15, we can see that for
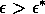 x reaches a stable equilibrium from any initial value, as indicated by the arrows. But for
x reaches a stable equilibrium from any initial value, as indicated by the arrows. But for
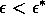 the equilibrium is unstable and the system is attracted instead toward
the stable limit cycle. The maxima and minima of the limit cycle (with
respect to x) are indicated by the solid circles. Notice that the amplitude of the limit cycle oscillations increases as
the equilibrium is unstable and the system is attracted instead toward
the stable limit cycle. The maxima and minima of the limit cycle (with
respect to x) are indicated by the solid circles. Notice that the amplitude of the limit cycle oscillations increases as
 decreases.
decreases.
Whereas phase portraits and time plots represent the dynamics of the system for a fixed set of parameter values, bifurcation diagrams summarize the dynamics for a whole range of parameter values. They show where stable equilibria or limit cycles can be expected, and can also indicate whether multiple stable states are possible at a given parameter value, or whether extinction can be expected. Thus, bifurcation diagrams provide more concise and complete information than other graphical methods (Collings et al. 1990). Each parameter can be varied in turn to see what effect it has on the dynamics. Hence, instead of using trial and error to locate the parameter combinations giving rise to oscillations or other behavior, we now have a more systematic method.
A drawback of the dynamical systems approach is that the mathematics required to obtain a bifurcation diagram can be quite formidable, especially when large models are involved. Fortunately, in recent years, many computer packages have become available to simplify the task. I used XPPAUT (Ermentrout 1994) and DSTOOL (Back et al. 1992) to obtain the results in this paper. XPPAUT has a graphical interface for the continuation and bifurcation package AUTO86 (Doedel 1981). I shall refer to AUTO rather than XPPAUT when making use of this interface. In
Appendix 3, I demonstrate how these packages can be used and illustrate the reliability of AUTO's routines by reproducing and, in fact, improving upon the results that Bazykin obtained by hand for his model (Eq. A2.1).
(see Appendix 2) are summarized in the two-parameter bifurcation
diagram in Fig. 16. This figure shows three regions in
Since A and B exchange stability in crossing from regions (i) and (ii)
to region (iii), we expect a transcritical bifurcation to occur as the
line with negative slope in Fig. 16 is crossed from regions (i) and
(ii) into region (iii). In crossing from region (i) to region (ii),
point A changes from stable to unstable and a limit cycle is
initiated. Thus, we expect a curve of Hopf bifurcations to divide
these regions.
I used XPPAUT to reproduce Bazykin's results. (A comprehensive,
interactive tutorial on how to use XPPAUT is available on the World
Wide Web at the address
ftp://mthbard.math.pitt.edu/pub/bardware/xpptut/start.html.
The tutorial can also be obtained via anonymous ftp from
ftp.math.pitt.edu in the directory pub/bardware). The
required driving program containing the model equations and parameter
values is shown at the end of this appendix A3.1. As can be seen, it
is very straightforward. In order to use AUTO to create a bifurcation
diagram, we need a starting point that must be an equilibrium
point. By choosing values of 0.3 for
I then used AUTO to vary
These are obtained by setting the right-hand sides in the
predator-prey equations (see Eqs. A2.1) equal to zero and solving for
x and y. As expected,
In the range
AUTO can be used to continue the Hopf bifurcation at
Note that the curve of Hopf bifurcations is very different from
Bazykin's straight line in Fig. 16. I will return to this point
shortly. A second observation is that, for the given values of
a, b, c, and d , a Hopf bifurcation (and
hence limit cycle behavior) is only possible if
It is not possible to continue transcritical bifurcations in two
parameters using AUTO, as they are structurally unstable unless the
system possesses intrinsic symmetry. However, if
Bazykin's model is simple enough that the curves in Fig. 19 can be
determined analytically, although the algebraic manipulations are
rather tedious. It can be shown that transcritical bifurcations occur
along the straight line
and Hopf bifurcations occur along the curve
(A description of the methods involved in calculating these curves can
be found in Guckenheimer and Holmes (1983) or Wiggins (1990). I used
MAPLE (Waterloo Maple Software 1990-1992) for some of the algebraic
manipulations. I have only included these expressions here to show the
accuracy of AUTO's results. The availability of packages such as AUTO
precludes the need for the reader to perform such mathematical
manipulations.) These are exactly the curves shown in Fig. 19. Hence,
AUTO's results are more accurate than Bazykin's linear
approximation (Fig. 16) for the Hopf bifurcation curve. The new
regions (i), (ii), and (iii) are shown in Fig. 19. XPPAUT or DSTOOL
can be used to obtain phase portraits and time plots corresponding to
different parameter combinations in Fig. 19. Due to space
considerations, I have not included any such diagrams here. Time plots
are useful for indicating the speed with which the stable equilibrium
or limit cycle is attained and the period of the limit cycle, if
applicable. If a system takes a long time to approach an attractor,
then the transient dynamics may be of greater practical importance
than the long-term behavior.
This section has shown how to rederive Bazykin's work (1974) on the
system of Eqs. A2.
more accurately and without having to completely understand the mathematical techniques involved. It has also established some confidence in AUTO's results.
USING XPPAUT TO STUDY BAZYKIN'S PREDATOR-PREY MODEL
Bazykin's results (1974) for the predator-prey model
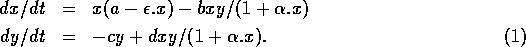
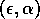 -parameter space, each
corresponding to a different form of qualitative behavior. In region
(i), there is a spiral attractor (say A) at which both x
and y are nonzero, as well as a saddle point (say B) on
the x -axis to the right of A. In region (ii), A is an
unstable source surrounded by a stable limit cycle and B is still a
saddle point on the x -axis. In region (iii), B is now
the attractor and A is a saddle point, but A has moved into the fourth
quadrant.
-parameter space, each
corresponding to a different form of qualitative behavior. In region
(i), there is a spiral attractor (say A) at which both x
and y are nonzero, as well as a saddle point (say B) on
the x -axis to the right of A. In region (ii), A is an
unstable source surrounded by a stable limit cycle and B is still a
saddle point on the x -axis. In region (iii), B is now
the attractor and A is a saddle point, but A has moved into the fourth
quadrant.
 and 0.1 for
and 0.1 for  , we can either determine such a point
analytically (as Bazykin did), or we can use XPPAUT to perform the
task numerically.
, we can either determine such a point
analytically (as Bazykin did), or we can use XPPAUT to perform the
task numerically.
 . AUTO locates a transcritical
bifurcation (see Appendix 2) at
. AUTO locates a transcritical
bifurcation (see Appendix 2) at 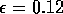 and a Hopf bifurcation at
and a Hopf bifurcation at 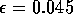 , together with stable
limit cycles (see Fig. 17). Since
, together with stable
limit cycles (see Fig. 17). Since 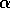 is fixed in Fig. 17, this
one-parameter diagram describes the dynamics along a horizontal line
at, say,
is fixed in Fig. 17, this
one-parameter diagram describes the dynamics along a horizontal line
at, say, 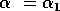 in
Fig. 16.
in
Fig. 16.
FIGURE 17:
One-parameter bifurcation diagram obtained by varying
 in Bazykin's model with
in Bazykin's model with 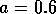 ,
, 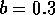 ,
, 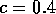 ,
,
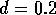 and
and 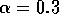 . The labels A and B mark the continuation
branches corresponding to the equilibrium points, HB stands for
Hopf bifurcation and BP for bifurcation point (transcritical in
this case).
. The labels A and B mark the continuation
branches corresponding to the equilibrium points, HB stands for
Hopf bifurcation and BP for bifurcation point (transcritical in
this case).
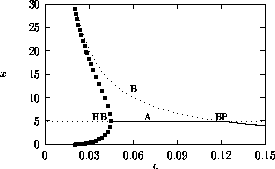
In Fig. 17, I have labeled the continuation branches A and B to
indicate which equilibrium point corresponds to which branch (see
Appendix 2 for a description of a continuation branch). Notice that
the x -coordinate of A does not vary with  , but the x
-coordinate of B does. The analytical forms of the equilibrium
points, which are given by
, but the x
-coordinate of B does. The analytical forms of the equilibrium
points, which are given by
 does not appear in the x
-coordinate for A, but does appear in that for B.
does not appear in the x
-coordinate for A, but does appear in that for B.
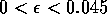 , point
A is unstable and B is a saddle point (see Appendix 2). There is also
a stable limit cycle surrounding A. Hence, these values of
, point
A is unstable and B is a saddle point (see Appendix 2). There is also
a stable limit cycle surrounding A. Hence, these values of  correspond to region
(ii) in Fig. 16. For
correspond to region
(ii) in Fig. 16. For 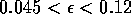 , A is a stable equilibrium point and
B is again a saddle point. This configuration corresponds to region
(i) in Fig. 16. For
, A is a stable equilibrium point and
B is again a saddle point. This configuration corresponds to region
(i) in Fig. 16. For 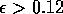 , B is now stable and A is a saddle
point, but the numerical output from AUTO shows that the y
-coordinate for A is negative for these values of
, B is now stable and A is a saddle
point, but the numerical output from AUTO shows that the y
-coordinate for A is negative for these values of  . This corresponds to
region (iii) in Fig. 16.
. This corresponds to
region (iii) in Fig. 16.
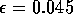 in
in
 as well as
as well as
 , resulting in a two-parameter bifurcation diagram. This is shown in
Fig. 18.
, resulting in a two-parameter bifurcation diagram. This is shown in
Fig. 18.
FIGURE 18:
Two-parameter continuation of the Hopf bifurcation shown
in Figure 17.
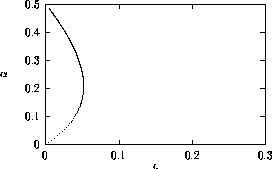
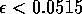 and
and 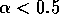 , which is a fairly small region of
parameter space and, hence, probably not of much biological
significance. (AUTO slows down considerably as
, which is a fairly small region of
parameter space and, hence, probably not of much biological
significance. (AUTO slows down considerably as 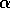 increases toward 0.5 and
increases toward 0.5 and  tends to 0 and never
actually reaches this point, although the curve does get very close if
AUTO is left to run for a sufficiently long time period. It can be
verified analytically that the curve does pass through
(0,0.5). However, complex behavioral changes occur at this point,
which is why AUTO has computational difficulties.)
tends to 0 and never
actually reaches this point, although the curve does get very close if
AUTO is left to run for a sufficiently long time period. It can be
verified analytically that the curve does pass through
(0,0.5). However, complex behavioral changes occur at this point,
which is why AUTO has computational difficulties.)
 is fixed at a number of different
values and one-parameter bifurcation diagrams similar to Fig. 17 are
created by varying
is fixed at a number of different
values and one-parameter bifurcation diagrams similar to Fig. 17 are
created by varying  in each case, then the values corresponding to transcritical
bifurcations can be recorded. An approximation to the two-parameter
curve can then be drawn through these points. Figure 19
shows the resulting curve, together with the Hopf bifurcation continuation.
in each case, then the values corresponding to transcritical
bifurcations can be recorded. An approximation to the two-parameter
curve can then be drawn through these points. Figure 19
shows the resulting curve, together with the Hopf bifurcation continuation.
 ,
,
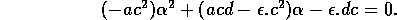
3.1 Computer listing for Bazykin model
- # Model equations.
- dx/dt=a*x-b*x*y/(1+alp*x)-eps*x*x
- dy/dt=-c*y+d*x*y/(1+alp*x)
- # Initial values.
- x(0)=0.2
- y(0)=0.2
- # Parameters and nominal values.
- param a=0.6,b=0.3,c=0.4,d=0.2,alp=0.3,eps=0.001
- done
ANALYSIS OF A SHEEP-HYRAX-LYNX MODEL
A4.1 Introduction This model is an example of a system dynamics model and has four main components: sheep, hyrax (Procavia capensis Pallus), lynx (Felis caracal Schreber), and pasture. In section A4.2, I discuss traditional methods that have been used to solve and analyze such models. In section A4.3, I give some background and a few technical details needed to use XPPAUT for analyzing the dynamics. Section A4.5 contains the model analysis. I begin by studying the effects of various parameters and density-dependent functions on the behavior of the model. This analysis shows the limitations of a traditional sensitivity analysis and highlights dynamics that are biologically implausible, namely that pasture growth is unlimited when sheep densities are low. A modification to the pasture growth term is discussed in section A4.5.4. The quantity of most interest to farmers is revenue. A two-parameter study of the effects of culling rates on farmers' revenue completes the analysis. This is followed by section A4.6, which interprets the main results from a biological viewpoint.
A4.2 Dynamic models and systems analysis: some background The systems approach to modeling was made popular by Forrester in the early 1960s (Forrester 1961). This approach involves dividing a system into a large number of very simple unit components (Watt 1966) and then using equations to describe the processes affecting each of these components. The methodology was originally applied to industrial, urban, and world population systems, but its utility has been extended to ecological applications by a number of researchers (e.g., Watt 1966, Jeffers 1978). A variety of aspects, such as age structure, developmental rates, and density-dependent relationships, can be included explicitly, thus increasing the realism of the model. Kowal (1971) notes that an analysis of dynamic models can provide approximations to ecosystem dynamics long before traditional experimental approaches can provide more detailed conclusions. Insights can also be obtained into aspects of the system that may otherwise be obscured by its complexity. However, dynamic models usually involve many equations (generally ordinary differential equations) and parameters, making their behavior difficult to predict (Patten 1971).
Traditionally, numerical routines have been used to obtain solutions over time for a given set of parameter values. Optimization routines are also often employed (Maynard Smith 1974) to determine the "best" possible strategy with respect to a cost or revenue function. These routines are implemented using computers (see Patten 1971, Gerald and Wheatley 1989, Hultquist 1988).
Although these methods are useful, their results depend on the particular parameter set used. Hadamard (1952) notes that since data in nature are never fixed, a mathematical model cannot be considered as corresponding to a physical phenomenon unless small variations in the parameter values lead to small changes in the solution given by the model. Attempts to heed this caveat have been based on the ideas of Tomovic (1963), and are often referred to as sensitivity analyses. These involve changing the values of the input variables and parameter values by a small amount (say 1% or 10%) and seeing whether these changes produce large or small variations in the performance of the model (Brylinsky 1972, Jeffers 1978). A sensitivity analysis does give some idea of the robustness of model predictions, but the information is limited in that only a single, small perturbation of each parameter is considered. (A method for perturbing a combination of parameters in order to find a "worst" case has been proposed by Hearne (1987), but it is not yet commonly used.) The dynamical systems techniques show the effects of a whole range of parameter values on the system.
A4.3 Model equations Swart and Hearne (1989) developed a dynamic model to study the impact of hyrax (Procavia capensis Pallas) and lynx (Felis caracal Schreber) on sheep farming in a region in South Africa. Two main problems were identified. The first involves competition for pasture between hyrax and sheep; hyrax encroach on farm land when the hyrax population exceeds the carrying capacity of wilderness areas in the region. The second problem is the predation on sheep by lynx. The principal food for lynx is hyrax, but lynx prey on sheep from time to time. The latter problem is of direct concern to farmers; they tend to be more tolerant of the competition with hyrax.
Swart and Hearne (1989) developed their model to increase understanding of problems caused by the spillover of hyrax and lynx from their predator-prey system into the sheep-pasture system, and to determine the effects of different culling strategies for hyrax and lynx. There are 10 state variables in the model. The sheep, hyrax, and lynx populations are each divided into three classes: juveniles, female adults, and male adults. There is one variable representing pasture. The quantity of most interest to farmers is revenue. This auxiliary variable is a function of the state variables and is made up of wool sales, mutton sales, the value of sheep stock, and the cost of culling hyrax and lynx.
Swart and Hearne (1989) used optimization routines to find the hyrax and lynx culling rates that gave maximum profitability in terms of revenue. They also investigated the system's sensitivity to parameter perturbations. They found that lynx culling is essential and that substantial increases in both sheep numbers and revenue are possible by simultaneously culling hyrax and lynx. Optimal culling rates, in terms of revenue, are ~ 30% per annum for both hyrax and lynx. From a policy point of view, the model is robust with respect to small parameter variations.
My purpose is not to redo the work done by Swart and Hearne (1989), whosemodel and analysis have accomplished their aims. Instead, I want to illustrate the usefulness of the dynamical systems software in this setting.
A4.4 Technical details A few minor modifications to the model are required to facilitate the use of this software. The first involves scaling the state variables so that they all have the same order of magnitude. Combining quantities of very different magnitude may lead to computer round-off errors (Gerald and Wheatley 1989). I chose values close to the initial values in Swart and Hearne (1989) as scaling constants si (see A4.7).
Secondly, in order for the computer packages to generate continuous bifurcation diagrams, all functions in the model need to be continuous. The original model uses two step functions to represent farmers' sheep-culling strategies. I replaced these with continuous functions having steep slopes in the region of the step.
In the original model, pasture production and fecundity rates vary seasonally. Since this complicates the dynamics considerably when it comes to parameter studies, and since the present study is more concerned with long-term equilibrium behavior than with day-to-day variations, I did not include the seasonality functions. Solving the system of equations numerically over time is still the best way to study seasonal variation, in most cases.
The various versions of AUTO only allow a state variable, or the L2-norm of the state variables, to be displayed on the y -axis of the bifurcation diagrams they generate. The L2-norm of a vector v = (v1, ... , vm) is given by

In order to have direct access to revenue values, it would be most convenient if revenue were a state variable. The following suggestion by Bard Ermentrout makes this possible.
Let v be the vector of existing state variables and let h(v) be the revenue function. We can add to the original system the equation
 ,
,
where
 is a small parameter. R is the variable that we want to represent revenue. This ordinary differential equation will not affect system equilibria because, at these points, R = h(v) and, hence, dR/dt = 0 (as required for an equilibrium value). The existence and stability of phenomena such as periodic orbits (limit cycles) are also not affected. Since
is a small parameter. R is the variable that we want to represent revenue. This ordinary differential equation will not affect system equilibria because, at these points, R = h(v) and, hence, dR/dt = 0 (as required for an equilibrium value). The existence and stability of phenomena such as periodic orbits (limit cycles) are also not affected. Since
 acts as a delay time, we would like it to be small so that R is a close approximation to revenue. However, care must be taken in the choice of
acts as a delay time, we would like it to be small so that R is a close approximation to revenue. However, care must be taken in the choice of
 , because very small values can give rise to computer truncation errors. For the current problem,
, because very small values can give rise to computer truncation errors. For the current problem,
 = 0.05 was used.
= 0.05 was used.
A4.5 Model analysis
A4.5.1 Reference parameter values
An initial set of parameter values needs to be chosen before the effects of varying parameters across ranges of values can be determined. Most of the values are given in Swart and Hearne (1989). Only values for the hyrax and lynx culling normals (HCN and LCN) need to be chosen. It seems most natural to choose those values that give the maximum revenue at equilibrium. I first fixed LCN at 0.1, chose a value of 0.2 for HCN (any reasonable values would do just as well), and used a numerical solver in XPPAUT to integrate the system of equations until an equilibrium point was reached. Using this equilibrium point as the initial point, I then used the AUTO interface to vary HCN. This exercise was repeated for a few different values of LCN.A value of 0.35 for HCN was optimal (in terms of revenue) for all values of LCN. I chose this value for HCN and then used XPPAUT to vary LCN in order to find the corresponding optimal value for LCN. The result was LCN = 0.15.
A4.5.2 The effects of culling sheep
Many parameters in this model could be used to illustrate the dynamical systems techniques. Those affecting population growth rates probably have the greatest influence on the dynamics. For illustrative purposes, I will discuss the sheep female culling normal SFCN, which is the average number of ewes culled by a farmer per year. As before, I used XPPAUT to integrate the system numerically, using the reference parameter values, until an equilibrium was reached. Using these equilibrium values for the state variables as the starting point, I employed XPPAUT's AUTO interface to produce a bifurcation diagram. Figure 20 shows the diagram with equilibrium revenue, the equilibrium number of lynx females, and the equilibrium amount of pasture on the y-axis, respectively.Note that AUTO encounters points beyond which it cannot calculate: SFCN=0.54 is such a point. Using XPPAUT to solve the system of equations numerically for parameter values on either side of this limiting point, we can determine the causes of the difficulties. Output from a numerical integration is shown in XPPAUT's data window, and from this we see that the sheep population dies out for SFCN >0.54. Beyond the limiting value, there is no equilibrium at which all three populations are present and, hence, AUTO cannot continue the equilibrium branch any further.
A second observation can be made by looking at the bifurcation diagram for pasture in Fig. 20. As the equilibrium number of sheep declines (as SFCN increases and approaches the value corresponding to sheep extinction), the equilibrium value for pasture increases rapidly (and AUTO encounters numerical difficulties). Clearly, this is unrealistic and suggests that some modification should be made to the model equations to limit pasture growth. I return to this in section A4.5.4. Before modifying the equations to limit pasture growth, it is informative to study the roles of the existing density-dependent functions. This can be viewed as another form of sensitivity analysis, in which we investigate the system's response to whole functions instead of single parameters.
A4.5.3 The effects of density dependence
A number of functions in the model modify growth and death rates as conditions change. All these functions are normalized to take the value 1 when the quantities on which they depend are at their reference values. For example, the equation governing pasture (P) dynamics is given bydP/dt = pasture production - pasture grazing = A.PPN - TSSU.GN.GM(PA),
whereAis the area of the farming region under study; PPN is the pasture production normal (average pasture growth rate); TSSU is total small stock units (a representative value for the number of sheep); GN is the grazing normal (average amount of pasture grazed per unit stock); and GM is the grazing multiplier, which is a function of PA, the pasture availability index. PA is given by
 ,
where P is an average pasture density. The grazing multiplier is an increasing function of PA, which reaches a maximum of 1.5 around PA = 3 and has a value of 1 at PA = 1.
,
where P is an average pasture density. The grazing multiplier is an increasing function of PA, which reaches a maximum of 1.5 around PA = 3 and has a value of 1 at PA = 1.
To remove a density-dependent function from the model, the simplest approach is to replace it by a constant function. For example, we can set GM equivalent to 1. This was done for each multiplier function in turn, and bifurcation diagrams obtained from the altered model were compared with those from the original model in each case.
Removing the grazing multiplier, GM, had the greatest effect on model dynamics. Even after I altered a number of parameter values, the system did not reach equilibrium. The sheep population either increased indefinitely or decreased to extinction for each parameter set that was tried. This is not surprising, since the grazing multiplier affects pasture grazing and sheep fecundity as well as sheep juvenile deaths. Without GM, the density dependence of pasture grazing and sheep dynamics on pasture availability ( GM is a function of PA) is removed. The results show that this density dependence is critical for regulating the sheep-pasture subsystem.
The effects of the other functions in the model were quantitative rather than qualitative. That is, removing them from the model tended to decrease the range of parameter values over which sheep, hyrax, and lynx coexist at equilibrium, but did not alter the qualitative dynamics. This does not imply that these other functions play an insignificant role in the model. They have a regulatory effect and reduce the impact of parameter changes on model behavior. This resilience to disturbances is very desirable (Holling 1973) and is expected of many natural systems. I observed earlier that the model lacks a feedback relationship that would limit pasture growth when sheep densities are very low. Also, pasture availability has a significant influence on pasture grazing and sheep fecundity and, hence, on the predictions of the model. In the next section, Eq. A4.1 is modified to include density-dependent growth.
A4.5.4 Adding density dependence to pasture growth
Equilibrium pasture values only become unrealistic for extreme parameter values. However, it is desirable to have a model that can describe a variety of situations, instead of one that is only suitable for a small range of values. Also, improving model realism in extreme regions may affect the dynamics corresponding to more normal values, and so play an important part in understanding system behavior. The formulation of a model also affects statistical parameter-fitting routines. If important relationships are left out, then these routines may give misleading results or fail to converge.In the sheep-pasture-hyrax-lynx model, pasture growth occurs at a fixed rate and is independent of existing pasture density (see Eq. A4.1). In order to limit pasture growth, I included a pasture multiplier (PM) in Eq. A4.1 as follows:dP/dt = pasture production - pasture grazing = A.PPN.PM(PA) - TSSU.GN.GM(PA),
where PM is a function of pasture availability, PA. For high values of PA, we expect pasture growth to slow down and saturate. We also expect a decline in growth when PA is very low. A function having this general form is the Ricker function (see Fig. 21).
FIGURE 21:
The pasture multiplier ( ) as a function of pasture
availability (
) as a function of pasture
availability ( ).
).
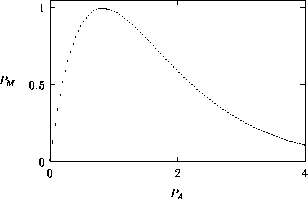
To test the effects of this new function, I generated a number of bifurcation diagrams and compared them with those from the original model. Figure 22 shows those diagrams that correspond to Fig. 20.
In Fig. 22a, total revenue declines to zero as SFCN increases. This is more mathematically satisfactory than Fig. 20a, where the curve stops abruptly at a positive revenue value, because it indicates clearly where a positive sheep population is no longer possible. Figure 22c shows the maximum pasture density that occurs when a positive sheep equilibrium (and hence, a positive value for revenue) is impossible. This density is lower than in Fig. 20c, but depends on the exact nature of the pasture multiplier.
Another observation from Fig. 22 is that, instead of AUTO being unable to converge at very low SFCN (sheep female culling normal) values, a Hopf bifurcation occurs, and the bifurcation diagrams show that no stable equilibrium at which all three populations coexist is possible for SFCN < 0.059. For these values, there is insufficient pasture to support the high sheep population. Thus, introducing the pasture multiplier has improved the dynamics at low values of SFCN as well as high values, and has solved the problem of revenue increasing rapidly as in Fig. 20a.
Using XPPAUT to integrate the system numerically gives insight into the dynamics corresponding to the different regions in the bifurcation diagrams. In particular, the temporal dynamics show that the pasture multiplier slows and limits pasture growth as desired. Comparing the dynamics of the original and modified models at SFCN = 0.5 shows that limiting pasture growth has a stabilizing influence on the dynamics (see Fig. 23 ). The oscillatory approach to equilibrium by the original model (Fig. 23a) is replaced by a smooth approach in Fig. 23b.
FIGURE 23:
Time plots obtained using (a) the original model and (b)
the modified model with 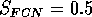 .
.
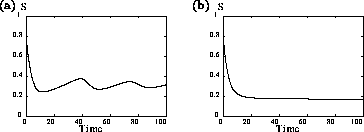
The limiting value for pasture in Fig. 22c is still rather high, but I had no experimental data on which to base the form of the pasture multiplier, and did not think it worthwhile to fiddle with the function to obtain a more plausible value. Effects of introducing the multiplier have been adequately demonstrated already.
A closer look at the behavior of the model may suggest further modifications of the equations. I have shown just one example of how bifurcation diagrams can help in the process of model building. The next section describes how two-parameter studies can be used to obtain useful summaries of model behavior.
A4.5.5 A summary of the effects of culling both hyrax and lynx
Swart and Hearne (1989) originally developed their model to study the effects of culling hyrax and lynx. In their model and in previous sections of this appendix, optimal values (with respect to revenue) were found for the hyrax and lynx culling normals. However, only one parameter was varied at a time. A two-parameter diagram summarizing the effects of varying both parameters simultaneously can be obtained as follows.Using the modified model, the bifurcation diagrams for the lynx culling normal LCN have the form shown in Fig. 24 . For LCN below the limit point, the sheep population dies out under too much predation by lynx. Using AUTO, the limit point can be continued in HCN, the hyrax culling normal, as well as LCN. That is, we can see how the position of this limit point varies as a function of both HCN and LCN. This gives the two-parameter bifurcation diagram in Fig. 25 . From this figure, it can be seen that sheep become extinct as a result of the combined effect of lynx predation and competition with hyrax for pasture, since both LCN and HCNare low in the region where sheep die out.
FIGURE 24:
One-parameter bifurcation diagram of revenue as a function
of  for the modified model. The change in stability (denoted
by the change from a solid to a dotted line) occurs at a limit point.
for the modified model. The change in stability (denoted
by the change from a solid to a dotted line) occurs at a limit point.
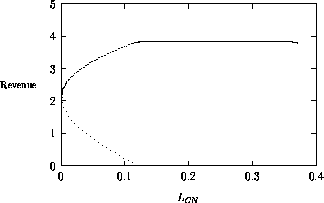
FIGURE 25:
Two-parameter continuation of the limit point in Figure 24.
(To determine the behavior corresponding to a particular region in this
two-parameter diagram, choose values for 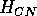 and
and  in this
region and then use XPPAUT to integrate the system numerically.)
in this
region and then use XPPAUT to integrate the system numerically.)
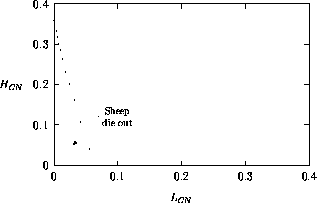
If Fig. 25 is combined with the observation that the lynx population dies out for LCN ~> 0.37 for all values of HCN, the result is
Fig. 26
. This observation was made by generating bifurcation diagrams for LCN for a number of different (fixed) HCN values. Conversely, varying HCN for a variety of fixed LCN values does not produce any parameter ranges where the hyrax population dies out.
FIGURE 26:
Two-parameter bifurcation diagram of the  and
and  parameter space for the modified model.
parameter space for the modified model.
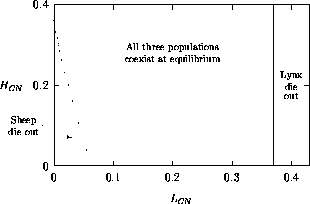
Figure 26 shows that all three populations coexist at equilibrium for a large set of culling rates. The diagram would be of even greater use if the revenue value corresponding to each point in this two parameter space were known. This can be done by recording information given by XPPAUT and using some other graphics package to plot a three-dimensional surface.
Using the modified model developed in the previous section, I fixed the value of HCN, chose LCN = 0.15 (say), and used XPPAUT to find the equilibrium point numerically. I then used the AUTO interface to vary LCN in both directions. Using the GRAB feature of XPPAUT to move along the branch of equilibrium points, I recorded the revenue values at regular intervals along the curve. I did this for a number of HCN values and plotted the results using the public domain graphics package GNUPLOT (Williams and Kelley 1986). A surface plot and corresponding contour plot are shown in Fig. 27 . As can be seen from the figure, there is a large region of parameter space over which revenue does not vary much, indicating that the model is very robust to changes in the culling rates in this region. This is a desirable property when it comes to developing management strategies.
A4.6 Conclusions The analysis of the previous sections has led to a number of insights into the sheep-pasture-hyrax-lynx system. Figure 22 shows that altering the number of ewes that are culled only affects the sheep-pasture subsystem. However, the effects on this subsystem are considerable. Culling too many ewes will obviously cause sheep numbers to decline. More important is the effect on revenue. Significant increases in revenue are possible if the farmer culls fewer ewes, because there is a greater return if these sheep are allowed to reproduce than if they are taken to market (provided that the sheep stock is not too large for the pasture to support it, i.e., provided SFCN > 0.059.) However, there is a trade-off: culling fewer ewes results in a lower cash flow. Another trade-off results from the decrease in pasture availability that accompanies a larger sheep stock. This is already reflected in the model by the dependence of sheep fecundity on pasture availability. However, an additional quantity representing the quality of sheep may be useful, as this will affect the returns from wool and mutton sales and, hence, revenue. This presents another opportunity for improving the model.
In section A4.5.3, I showed that density dependence of sheep and pasture dynamics on pasture availability is critical for regulating the sheep-pasture subsystem. In fact, this encouraged me to modify pasture growth to include density dependence. This modification restricts both pasture and revenue values from increasing indefinitely (compare Figs. 20 and 22) and also stabilizes the temporal dynamics (see Fig. 23). Other modifications, such as including the effects of hyrax grazing in the pasture equation, can also be made. In the interests of space, I have not discussed such a modification, but the approach in preceding sections indicates how such a modification can be introduced and studied.
Finally, the effects of culling both hyrax and lynx were summarized using two-parameter diagrams. In particular, Fig. 27 shows that the model is robust to changes in culling rates, provided that these rates are sufficiently high.
A4.7 Mathematical details for the sheep-hyrax-lynx model
A4.7.1 Modelling delays in system dynamics models
A system does not always respond immediately to a change in one of its components. Often there is a time lag between the initial change and the system response. For example, a change in hyrax population density will only affect hyrax population size in the following season. It takes time for an increase in population density to affect reproductive success of hyrax and survival of their offspring.
To represent this in the model, I use averaged or smoothed versions of certain quantities to calculate growth rates. Three quantities are averaged in this model: hyrax density (HD), prey abundance (AP), and the grazing multiplier (GM). Sheep fecundity and juvenile mortality are functions of the grazing multiplier average,
 ,
instead of GM. I use a first-order distributed delay (May 1973, MacDonald 1978) to calculate the averaged version, e.g.,
,
instead of GM. I use a first-order distributed delay (May 1973, MacDonald 1978) to calculate the averaged version, e.g.,
d
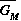 /dt = (
/dt = ( 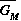 ) /tdel,
) /tdel,
where tdel is the average delay time. Examples of this type of delay equation are found in Forrester (1961). MacDonald (1978) provides a detailed explanation of the mathematics underlying this differential equation. This ordinary differential equation is added to the original system of model equations, thus increasing the dimension of the system to be solved. Fortunately, this increase in dimension does not pose a problem when solving the system numerically.
Further discussions of delays in biological systems and their effects on system behavior are found in May (1973) and MacDonald (1989). For the sheep-hyrax-lynx model, the delays did not affect stability, even for large average delay times.
A4.7.2 Rescaling model equations
Suppose the differential equation for the state variable vi is given bydvi/dt = fi(v1, ... , vi, ... , vm).
Let vi = si
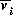 ,
then
,
then
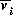 = vi/si
= vi/si
and
d 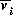 /dt = (1/si)(dvi/dt)= (1/si)fi(s1
/dt = (1/si)(dvi/dt)= (1/si)fi(s1 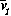 , ... ,si
, ... ,si 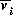 , ... , sm
, ... , sm 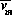 ).
).
Dropping the bars for convenience, we get
dvi/dt = (1/si)fi(s1v1, ... ,sivi, ... , smvm),
Address of Correspondent:
Lynn van Coller
28 Woodside Avenue
Cowies Hill, 3610, South Africa
phone: 27-31-728013
fax: 27-31-728013
lvcoller@nbsmail.nbs.co.za
*The copyright to this article passed from the Ecological Society of America to the Resilience Alliance on 1 January 2000.
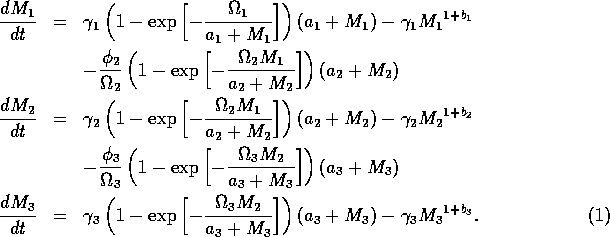
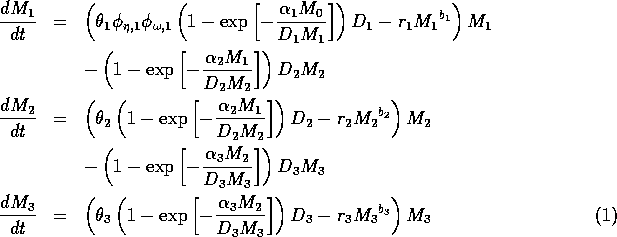 ,
,
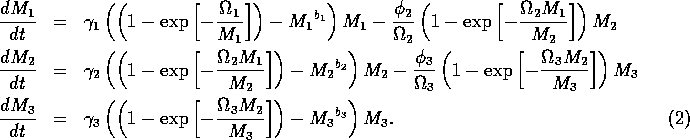

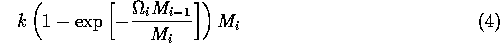 ,
,
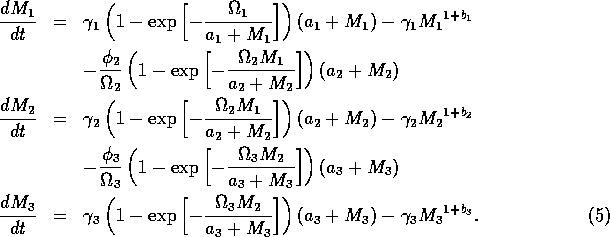 .
.
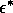 .
.
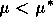 there are no equilibrium points at which both populations are nonzero.
there are no equilibrium points at which both populations are nonzero.
 (nominal value = 0.28/yr). In (a) revenue is plotted on the y-axis,
in (b) the state variable for lynx females is used, and in (c) the
state variable for pasture is used.
(nominal value = 0.28/yr). In (a) revenue is plotted on the y-axis,
in (b) the state variable for lynx females is used, and in (c) the
state variable for pasture is used.
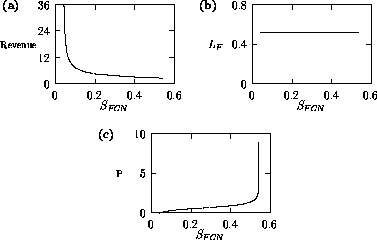
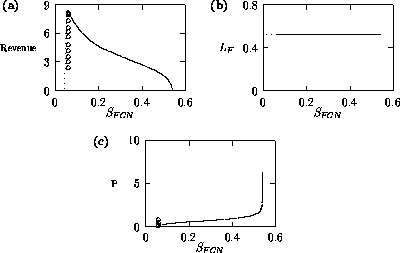
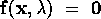 . Limit points and simple bifurcations can be computed on demand.
. Limit points and simple bifurcations can be computed on demand.